网格和物理模型在计算流体动力学中的应用研究

张亚勃，张东辉

（1.中国中原对外工程有限公司，北京100191；2.中国原子能科学研究院，北京102413）

1 CFD数值分析的基础：网格生成技术

作为现代研究手段的数值分析方法，无论研究领域如何，研究区域的离散，即网格的生成是必不可少的一部分，根据研究问题的复杂程度的不同，这部分的工作量几乎与进行求解计算的工作量相当。因此合理有效的网格生成技术非常重要。由于工作量很大，在网格生成方法上的选择主要以能生成合理的网格为原则，兼顾方法的简便性，同一控制体中也可采用不同区域灵活选取不同网格生成方法。网格生成方法大体可分为结构化网格和非结构化网格。结构化网格中，任意一个节点的位置可以通过一定的法则予以命名，当研究区域复杂时，不同区网格按照一定规律联接，形成块结构化网格，将控制体分解成不同的子域，每一子域中结构化形式可以不同，子域之间可以互不重叠也可以有部分重叠。非结构化网格中，节点位置无法用一个固定的法则予以有序的命名，非结构化网格由于对不规则区域的特别适应性而自20世纪80年代以来得到迅速发展，这种网格除了每一个单元及节点的几何信息必须储存外，与相邻单元的编号等信息也必须作为联系关系信息存储起来，这使得非结构化网格的信息量比较大。目前主流的CFD分析软件都兼容两种网格形式，并提供了各种各样的网格生产方法，在同一问题中还可同时应用这两种不同形式的网格混合使用，达到特殊形状模拟和提高计算效率的目的。

反应堆热工水力CFD模拟与传统的主要分析复杂外流场流动的航空空气动力学、内燃机械等不同的是：反应堆热工水力CFD分析的主要对象是被反应堆冷却剂所包围的反应堆内部构件，如堆芯组件、控制棒组件、主泵等，这些特殊结构的特点是设备全部或部分浸泡在冷却剂中，而同时设备内部也存在流体的流动，即在分析过程中既要考虑外流场的复杂流动现象，又要考虑内部流场的影响；同时在计算中普遍要耦合热效应。这给反应堆设备CFD网格模型的划分带来新的问题和挑战。近年来，基于各种不同类型的结构／结构杂交网格技术的开发，随着对复杂形状问题适应能力越来越迫切，一种新型的网格技术——多面体网格技术逐渐成为成熟的网格技术。在复杂网格生成与计算效率上，多面体网格提供了很好的平衡，相对于结构网格，多面体网格与非结构化网格一样简单、快捷的构建，而计算效率明显高于非结构化网格。对于应用于内流场形状十分复杂的结构，显示出了较大的适用性。目前在反应堆热工流体设计中，对堆芯组件内通道的模拟已经广泛地被应用（如图1所示）。

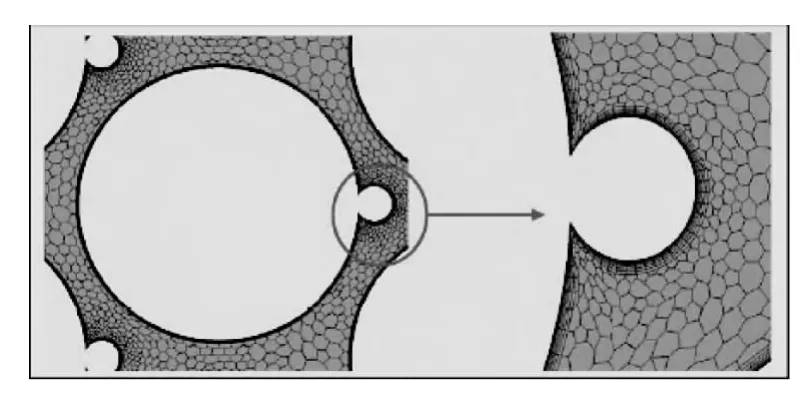
图1 某快堆燃料组件多面体网格模型Fig.1 Polyhedral meshed model for fast reactor assembly

2 数值分析的离散格式：有限容积法

对流-扩散问题数值计算的精度与效率，不仅取决于所生成网格的质量，同时也取决于对流项的离散格式（或差分格式）。在CFD研究领域里，对流项离散格式的构造一直是具有挑战性的研究热点之一，长期以来认为难以构造一种很好的模拟所有对流-扩散问题的对流项离散格式，因为在构造对流项离散格式时不仅要考虑对流项迁移特性，还要保证较高的计算精度，这本身是互相对立的。低阶格式如一阶迎风（FUD）格式是绝对稳定的，能很好地体现对流项的迁移特性，但有非常严重的假扩散。中心差分（CD）格式能很好地消除假扩散，但它是条件稳定的，当网格贝克莱数或网格雷诺数超过临界值时容易导致迭代发散。考虑到反应堆组件CFD分析具有特殊形状和边界条件，且需要耦合热效应分析，因此有必要选用一种高分辨率的格式。

就常用的数值计算方法而言，大致可分为三类：有限差分法、有限容积法和有限元法。在CFD发展初期，由于所研究问题的几何外形简单，容易生成规则的结构网格，可直接利用差分来近似微分方程的偏导数，因此有限差分方法得到很广泛的应用，随着CFD面对计算的外形越来越复杂，传统网格已经不能适应计算的要求，于是CFD工作者提出了分块结构网格、非结构化网格以及上文提到的多面体网格等，在这些网格上，传统的有限差分法已经不能再适用，为此相继发展了有限容积法和有限元法。

有限元法是基于变分原理提出的计算方法，在计算固体力学中得到广泛应用，CFD方面起步较晚，其主要原因是流体力学的控制方程较固体力学更为复杂，且方程性质随流场特性（如雷诺数、马赫数等）的不同呈现不同的性状，变分原理不好应用。有限元法求解难度和工作量较大，因此，目前来说有限元法的结算效率要低于有限容积法。

有限容积法通过对原方程（Euler和NS方程）在控制体单元内直接积分，并通过体积分到面积分的转化，将原方程的求解转化为表明通量积分；黏性项和对流项也可转化为通量面积分，从而求得单元内物理量平均值。由于对控制体性状没有特殊的要求，此方法特别适合于复杂形状流场的计算。因此，是进行反应堆内部流场计算的最佳选择。

以直角坐标系中的对流项为例，它的有限体积离散形式为：

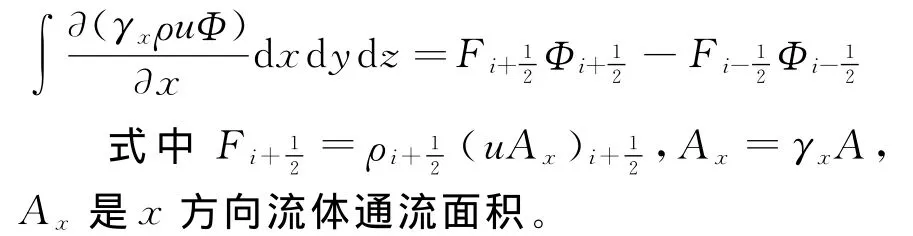
可由一阶迎风格式计算，对于对流占优的流动，迎风格式要优于中心差分格式，此时：

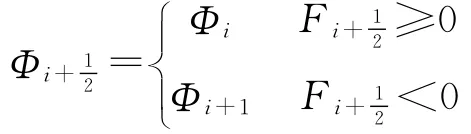
3 湍流模型：特殊形状控制体内流场分析处理方法

工程角度研究湍流的基本目的是精确预测与控制湍流。随着计算机技术的迅速发展，湍流的数值模拟精度几乎可以与理论研究和实验研究相比较，成为工程技术领域主要的分析手段。从求解方程上，湍流模型可以分为两类：一种是以NS方程为求解对象，一种则以分子动力学理论研究湍流流动。前者主要分为直接模拟（direct numerical simulation，DNS）、大涡模拟（large eddy simulation，LES）、雷诺平均法（Reynolds averaged Navier-Stockes，RANS）和基于概率方法的PDF（probability density function）。DNS是对非稳态NS方程直接求解，可以分辨所有尺度的涡，RANS求解雷诺平均方程，雷诺平均方程是不封闭的，必须引入雷诺应力的封闭模型才能进行求解。LES是介于DNS和RANS之间的数值模拟方法，对大尺度涡进行直接求解，小涡对大涡的影响采用经验模型近似处理。PDF则应用于湍流化学模拟反应方面较多。目前工程应用为目的的CFD分析大部分仍以雷诺平均法为主，虽然雷诺平均法需要引入较多经验参数修正，且分析精度相对低，但其优点是经过数十年的研究和应用，雷诺平均法已经发展得相当成熟，经过修整可以精确的模拟各种特性的流场，且计算效率高，能适应复杂流场，巨大网格数量的问题分析。因此，组件及冷却剂热工流体动力学设计和分析还是以雷诺平均法为主，而对于形体复杂的反应堆系统来说，进行雷诺平均法模拟是比较现实的。下面介绍几种实践中被认为较为适合的特殊流道湍流模型，对于更多的湍流模型可见图2，详细介绍可参考文献［2］。

3.1 矩形截面通道内湍流的大涡模拟

大涡模拟介于雷诺平均法模拟和DNS直接模拟之间，它既能反映控制体内大部分涡的运动特性，又简化了数量众多且影响较小的小尺度涡的直接模拟，提高计算效率，同时其计算精度要较雷诺平均法模拟高。近年来的发展，该模型能够对不规则形体进行较高效率的计算。在不规则管道或流场中，由于湍流的各向异性引起垂直于主流方向的二次流动，使得湍流和换热更加复杂。对于矩形管道内湍流的模拟，各向同性的涡黏模型不能预测湍流引起的二次流动，代数应力模型、非线性k-ε模型和各向异性低雷诺数模型经常被使用，但对二次流动的表达取决于经验参数，因此模拟出的湍流量与试验值不能完全一致。为更好地理解和揭示湍流机理和二次流动产生原因，直接模拟是一个重要的工具。许多研究者采用大涡模拟技术研究矩形通道内的流动和换热情况，这些研究成功地预测了截面内二次流动以及对平均流动和湍流统计的影响，且与试验是一致的［3］。

例如某矩形管道高为H，长为L，x为主流方向，y和z分别为展向，u、v、w分别表示各方向的速度分量，考虑重力影响，其大涡模拟物理模型描述如下：

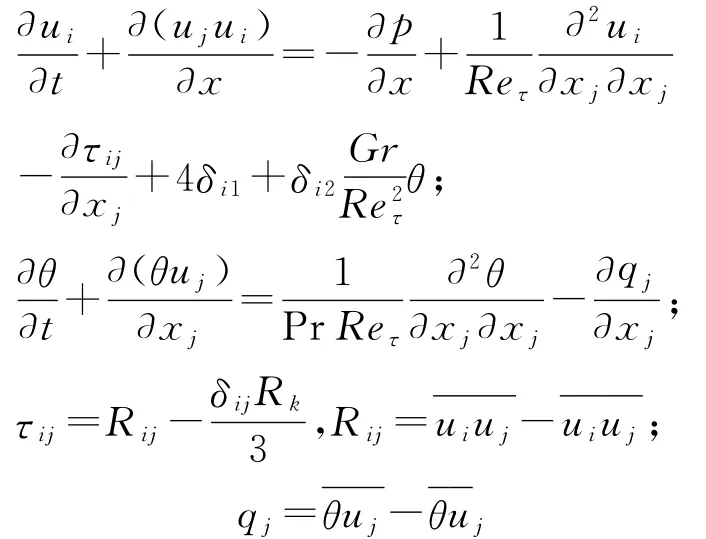
式中字母上方的“—”表示过滤量，无量纲温度的定义为：

根据理论抽样，本文选择在参与社区治理之初规制、规范和认知合法性均缺乏的LL老年社会工作服务中心(以下简称LL)作为案例。作为纯粹的“草根”(自下而上发起成立的)社会组织，LL成立于2006年，是一家致力于推动中国社区居家养老服务的民间机构。从志愿团队身份到企业法人身份，再到合法社会组织身份，并成为行业标杆组织，其合法化路径与行动策略显示出社会组织自下而上获得合法性的完整过程，较好地排除了组织资源、政治联系等其他因素对社会组织合法化进程的影响。

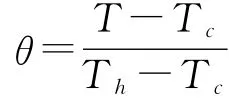
雷诺数和格拉晓夫数为：

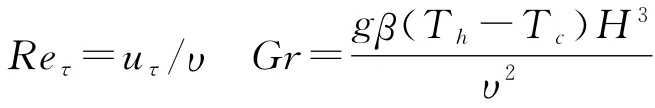
以上式中τij和qj分别表示亚格子湍流应力和热流密度，大涡模拟中，亚格子模型对大涡模拟具有重要影响，若采用动态涡黏模型表达则亚格子应力表示为：

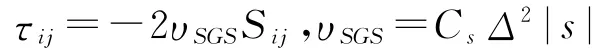
以下为某对流实验回路的模拟，装置的主要结构由右侧高温段、左侧低温段、下端加热段和上端冷却段组成。回路圆管直径60.3mm，壁厚5mm，其结构参数如图3所示。

图3 高温实验回路及其结构Fig.3 High temperature test loop and its diagrammatic sketch

管内流体为液态锂铅，其物性参数如下：

密度／（kg／m3）：

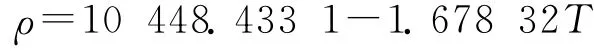
比热容／（J／kg·K）：

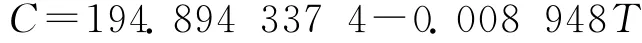
动力黏度／（Pa·s）：

利用CFD程序对高温热对流实验回路进行计算，计算结果见表1。回路上升段温度沿高度方向上的分布如图4所示。

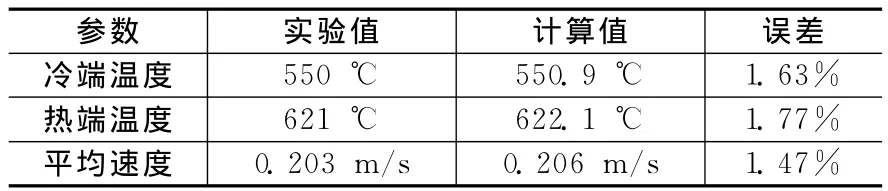
表1 计算与实验数据的对比Table 1 Comparison of calculated and experimental data

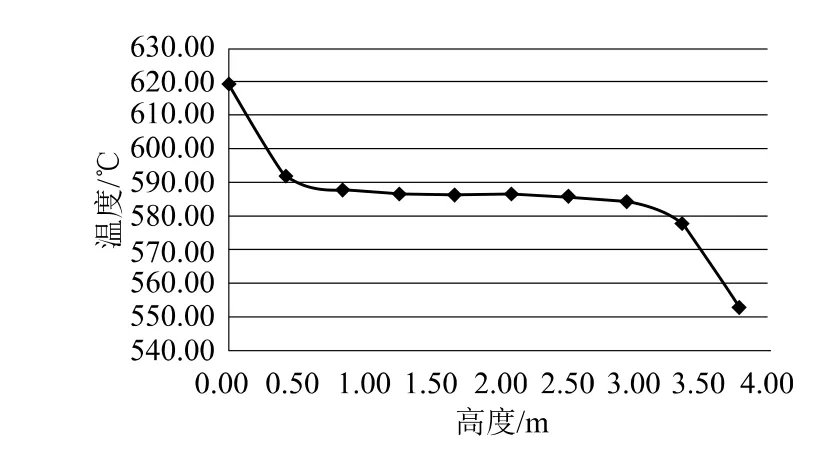
图4 回路上升段温度沿高度方向上的分布Fig.4 Temperature distribution along height direction

3.2 截面通道内存在孤岛湍流的雷诺平均模拟

雷诺平均法模型是在各向同性的前提下，将速度脉动的二阶关联量表示成平均速度梯度与湍流黏性系数的乘积，即：

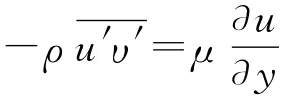
推广到三维问题，若用笛卡尔张量表示则有：

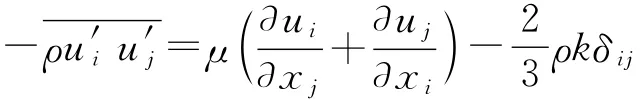
湍流模型或湍流封闭的任务就是给出计算湍流黏性系数的表达式或其输运方程的方法。根据建立微分方程的数目，可以分为零方程模型（代数方程模型）、一方程模型和双方程模型。由于该模型是基于各向同性的前提下，对于特殊形状通道的二次流计算需要对模型本身进行修正，以达到模拟二次流对主流影响的效果，如修正的k-ε模型，低雷诺数k-ε模型等。雷诺平均法模型计算效率非常高，适合计算复杂形状、网格数量大的问题。

在快堆液体悬浮式非能动停堆装置的设计中，悬浮式控制棒悬浮于液钠中间，属于流固耦合计算的孤岛问题。所谓孤岛的处理方法，是在采用整场离散、整场求解时，对于与计算边界相邻接的固体区域可以采用把固体区作为黏性无限大的流体区的方法来保证固体区中速度为零。当固体区位于流场中间而不与计算边界相连时采用的处理方法。当然该处理手段并不只限于处理孤立物体，而是一种通用性很强的处理流固耦合问题的方法。该方法具体实施步骤如下：①在每一层次的迭代计算前令障碍物区的速度u和为零，这样可保证对障碍物附近的节点速度起到滞止的作用；②在求解速度的方程时令障碍物区的离散方程的主对角线上的系数为一个极大值，如1 024，这样算出来的速度估计值u和v等于零；③再令障碍物区的速度修正公式里的系数d，d取一个极小值，如10～24，这样速度修正值也为零。关于障碍物绝热的边界条件，采用的是使障碍物和其邻近的流体温差等于零的方法。即在每一层次迭代计算前，令障碍物边界的节点上的温度值等于其邻近流体的温度。至于上下底边的绝热边界条件，按附加源项法处理时，其附加的常数源项为零。

同时，对于形状特殊，流道狭窄的堆芯控制棒等装置，在湍流模型的选取上应选用二次流修正较好，附加壁面影响的模型。徐建军等人采用染色法和数值计算相结合的方法研究冷态下矩形窄缝流道角部附近流场的分布，研究表明，相比较其他湍流模型，雷诺应力模型中的SSG模型能够模拟出矩形通道中湍流的各向异性，与可视化实验结果定性符合较好。标准k-ε模型在低雷诺数时符合较好，但随着雷诺数的增加，预测偏差增大。在较宽的雷诺数范围内，SSG模型与试验数据拟合的公式符合较好，尤其是随着Re的增加，偏差减小，在工程应用中，控制棒组件中的Re比较高，选用SSG模型是合适的，见图5。

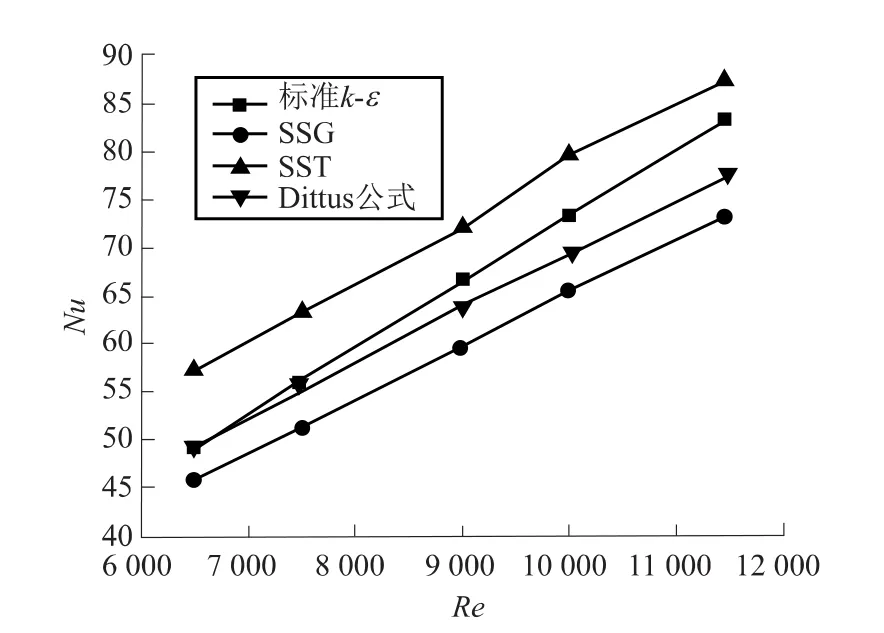
图5 试验数据与CFD计算结果比较Fig.5 Comparison of calculated and experimental data

4 发展趋势：两相流、多尺度耦合和并行计算的应用

两相流动和沸腾传热的计算分析是一项复杂的工作，因为通过气液界面的流动特性和传热特性变化较大，特别是密度的巨大变化和热导率的改变：与运用一维集总参数法进行两相流模拟的系统程序相比，CFD方法是基于求解空间两相流场内各相的质量守恒、动量守恒和能量守恒方程。两相流的模拟还无法达到单相模拟所能达到的精度。总之，模拟两相流动比单相流动CPD模拟更富有挑战性，但其潜力是巨大的，目前两相流动CPD模拟方法正在紧张而有序的研究发展中。

早在20世纪80年代Hirt等人提出了所谓流体域VOF（Volume Of Fluid）方法直接进行两组分、两相界向边界的数值模拟，但没有考虑相变热。VOF方法已经成为几乎所有模拟两相流动商用CFD程序的基础。近年来，随着多相流物理模型特别是两流体模型的发展，多相流动的数值模拟方法得到一些应用，开发了许多可用于模拟多相流动的CFD软件：CFX，lquent.FLOW3D，STAR—CD，Phoenix等。多相流的描述主要考虑总体的性能：压降、体积份额和传热率等。目前，根据主要模拟方法的原理，多相流动模拟方法主要包括直接数值模拟方法DNS（direct numerical simulation）、均相模型、欧拉—拉格朗日方法和两流体模型等。

尽管在工程和研究方面取得了一些进展，但对以两流体模型为基础的多维两相流的数值模拟仍处于发展阶段，并且流入流出边界很可能引起数值上困难和收敛问题。工程应用主要需考虑鲁棒性、CPU时间效率和准确性。并且多相流动的模拟不像单相流那样，仅提高网格的质量就能改善计算结果的准确性，物理模型的影响更为重要。

经过近半个世纪的研究，特别是近十年来的发展，CFD方法得到大力的发展和广泛的应用而且针对具体问题，如核工业中的问题必将推动CFD方法的进一步发展和完善，CFD方法使计算分析由一维向三维发展，并且三维CFD计算往往与一维系统程序计算进行耦合，即所谓多尺度耦合。现有许多项目就致力于类似的工作：例如，爱达荷州工程和环境国家实验室已与FLUENT软件公司联手将RELAP5—3D和FLUENT进行多尺度耦合。欧洲的ASTAR项目的目的就是在于将先进的CFD工具与系统程序（CATHARE或ATHLET）进行耦合，德国也正将CFX模拟和系统程序COCOSYS的计算进行耦合。近来就有学者使用多尺度耦合方法对反应堆堆芯进行研究。D.P.Weber等在2003年对微型堆芯（mini core）进行了耦合计算，使用了5 000 000CFD网格单元和150 000中子物理学区域。初步计算表明，如果采用万亿次级别的计算机，原型PWR堆芯的稳态计算能在一天内完成。但系统程序和CFD的耦合，仅限于稳态工况，系统程序为详细的CFD分析提供边界条件。高速和大存储量的计算机的发展使运用CFD方法可得到许多流动问题的数值解。

在核工业系统中，许多问题较为复杂，需要分析的对象几何结构尺寸较大，采用CFD方法进行研究时往往受到计算机计算能力的限制，因此必须采用并行计算方法。目前并行计算面临两个主要问题，一是如何将庞大的数据分配到不同的中央处理器上进行计算；二是并行计算方法的鲁棒性较差，Weber等人1999年用STARCD对单相、稳态情况下1／8个PWR堆芯内的温度分布进行了计算，以验证汽泡核心可能出现的位置，整个区域划分了2.5亿个网格单元，采用计算机群进行并行计算，如果要对该系统进行瞬态计算，则只允许划分数百万的网格。

5 不足与挑战

CFD方法应用于反应堆工程设计的过程中取得了很大的成就，但它毕竟还是一门年轻的学科，存在着很多困惑。

首先是可信度问题。对于绝大多数流动问题，还没有任何一个CFD方法可以给出定性的正确结论，或确定误差范围定量结果。一般采用同实验结果相比较的方法来验证CFD的可信度问题，但一方面，试验结果同样存在可信度问题，另一方面，实验结果往往很难给出精细的流动结构，而对细节的深入分析是CFD结果的重要信息。

其次，CFD理论的数学基础尚不健全。目前非线性偏微分方程组的数值解法尚未成熟，对三维流体力学建立的控制方程在进行计算处理时必须是经过简化的，Euler和N-S方程本身都是非线性方程组，针对标量方程构造的CFD计算格式通过特征分裂等方法扩展到这些非线性方程组后，其原来的一些特性就消失了。CFD的其他一些物理模型如湍流模型、化学反应模型、多相流模型等都远未发展完善，其计算精度和可靠性都存在目前无法解决的缺陷，解决这些问题可能需要很长时间的探索。

6 结语

越来越多的研究表明，今后CFD方法将由反应堆设计安全审查部门要求应用于安全评审。目前在开发新一代的反应堆时已经使用该研究方法，在第四代压水堆概念设计时，将应用CFD程序评估完整的压力容器特性，综合分析压力容器的热量和气体传输以及其对系统压力变化的反应性。随着现代计算机技术特别是超级计算机和并行计算集群等技术的发展，CFD方法逐渐开始摆脱计算机硬件的限制，其应用范围将大大扩展和丰富，成为反应堆工程设计与热工水力安全分析的主要手段。

［1］ 王福军.计算流体动力学分析［M］.北京：清华大学出版社，2004.

［2］ 林诚格，等.非能动安全先进核电厂AP1000［M］.北京：原子能出版社，2008.

［3］ Patankar，S.V.（1975），Numerical Prediction of Three-Dimensional Flows，Studies in Convection Theory，Measurement and Applications，Vol.1Academic，New York.

［4］ Fluent Inc.FLUENT User's Guide.Fluent Inc.2003.