波导与双环侧向耦合系统的透射谱特性分析

(杭州电子科技大学光学研究所，浙江 杭州310018)

0 引 言

微环谐振器具有尺寸小，结构简单，易于集成和具有高Q 模式等优点，在集成光学中备受关注[1]。通过比较发现，现有的关于微环腔的理论[2-4]都没有考虑到环间的相互作用，从实际出发，本文在波导双微环耦合系统的研究中，考虑了环间相互作用，进一步探索透射谱的物理特性[5]。本文基于波导双微环侧向耦合系统的耦合模式方程(coupled-mode equations，CMEs)，得到波导双环耦合系统的透射谱公式和相位谱公式，数值模拟微环损耗和透射率对波导双环耦合微环系统的透射谱和相位谱的影响。通过本文研究发现，两个微环的损耗和透射率均对透射谱和相位谱有着显著的影响。

1 理论分析

将光纤耦合器分两类:第一类是N个平行排列的光纤，并排在一个平面上，相邻光纤之间的耦合系数相同，忽略非相邻光纤之间的耦合，称之为线形排列弱同型耦合器;第二类是N个平行排列的光纤，并排在一个圆柱面上，首尾相连，相邻光纤之间的耦合系数不相同，忽略非相邻光纤之间的耦合，称之为线形排列弱异型耦合器[6]。通过比较发现:3×3 线性排列弱同型耦合器可以等价为波导双微环耦合系统[5-6]。忽略非相邻光纤1和3 之间的耦合。只考虑相邻光纤之间的耦合。设光纤1与2 之间的耦合参数为ξ，光纤2和3 之间的耦合参数为η。3×3 线性排列弱异型耦合方程可表示为如下形式[5]:

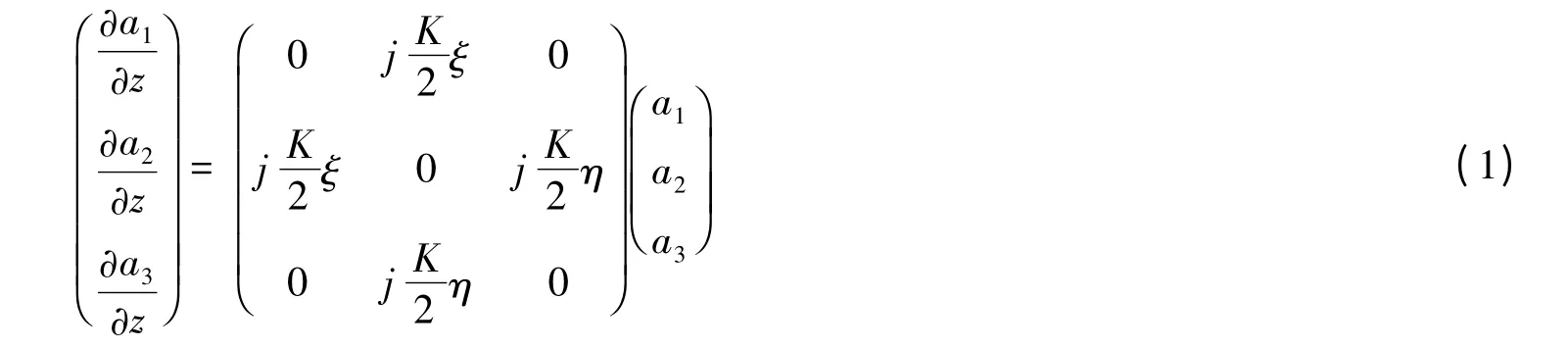
式中，Kξ/2和Kη/2表示不相邻波导间的耦合系数，ai为第i个波导的模式场。

令∂ai/∂z =-λai，i =1，2，3。忽略含时相位项，特征函数为ai(xm)= φi(xm)exp[jxm]，其中=Kz，m=1，2，3。假设且满足ξ2+η2=2，Δ为耦合强度。令λi=iKxi，求得特征值:

由于具有不同的特征值，根据本征函数构建解矩阵[5-6]:

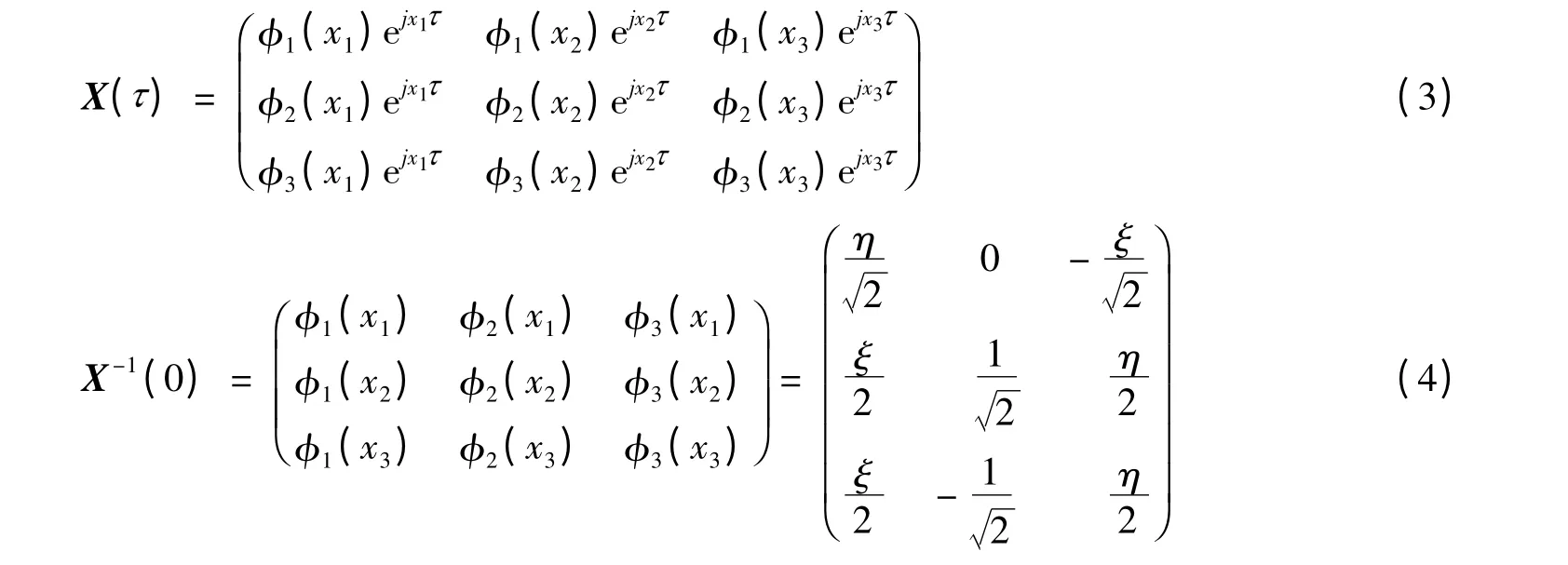
文献[3]中直波导和双环是共面的，直波导与环2的底部耦合，环2的顶部与环1的底部耦合。如图1所示，本文结构中，直波导和双环是不共面的。对于环2，光束沿着顺时针方向传输，有a2=α2exp[jθ]b2=B2b2。对于环3，光束沿着逆时针方向传输，有a3=α3exp[-jθ]b3=B3b3。相移θ=ωL/c，L为环的周长。其中，α2和α3为损耗系数，c为微环的相速度，ω为非共振时的角频率。为了简化讨论，输

入和输出关系可以通过传输矩阵表示出来:

单波导双微环耦合系统的透射谱公式为:

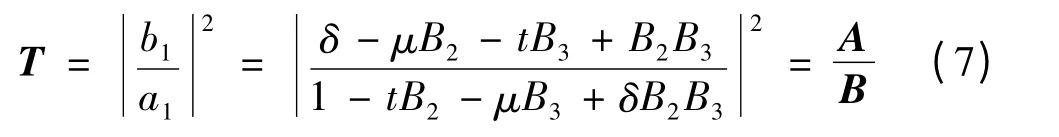
当dA/dθ=0时，透射谱极值点位于:

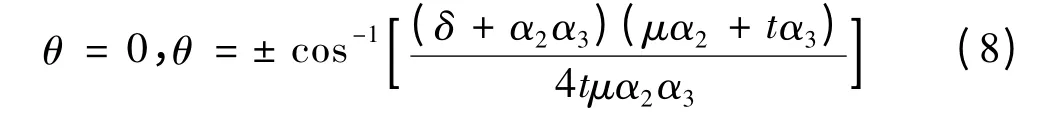
为了简化，取δ=α2α3，r=(δ+α2α3)/4α2α3=1/2，则有:

最大峰值所在的位置，对应θ=0;最小峰值所在的位置，对应式(9)。

相位谱公式为:

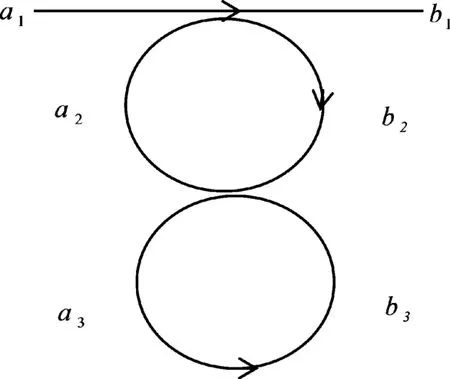
图1 波导双环耦合系统

2 数值模拟

纵坐标为透射谱，横坐标为由于色散而引起的频率失谐，用弧度θ 来表示。透过率t 也叫耦合传递系

数，即光的振幅通过耦合部分所能传输的几率。通过改变直波导和环2 之间的间隔来实现对环2 损耗的调节。通过改变环2和环3 之间的间隔来实现对环3 损耗的调节。

2.1 环2 损耗α2的影响

固定环3 损耗α3和透过率t，改变环2 损耗α2。取α3=0.999 9，t=0.8，α2分别取为0.60，0.65和0.70，其透射谱和相位谱如图2(a)和图2(b)所示。

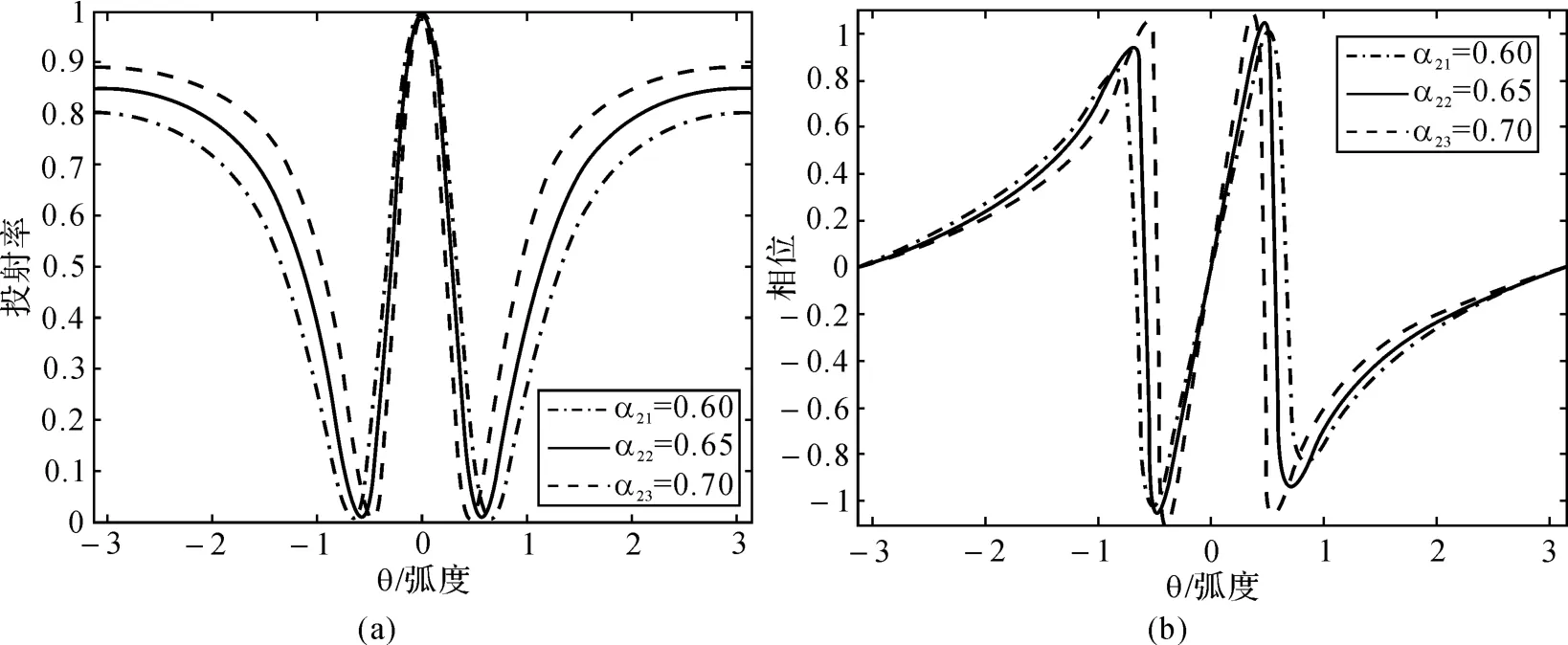
图2 环2 损耗分别对透射谱和相位谱的影响

透射谱都是电磁感应透明(electromagnetically-induced transparency，EIT)线型，随着环2的损耗α2增加，最高透射峰的位置保持不变，峰值都是1。最小透射峰所在的位置发生了变化，谱宽依次变窄。同时相位谱形状保持不变，谱宽变窄了，最高透射峰值下降。

2.2 环3 损耗α3的影响

固定环2 损耗α2和透过率t，改变环3 损耗α3。取α2=0.88，t=0.8，α3分别取为0.95，0.98和0.999 9，其透射谱和相位谱如图3(a)和图3(b)所示。

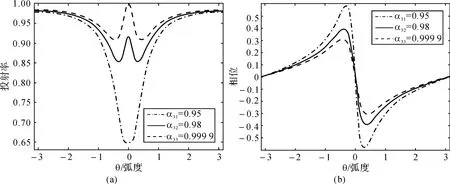
图3 环3 损耗分别对透射谱和相位谱的影响

随着环3的损耗α3增加，透射谱从EIT 线型变为洛仑兹线型。此处的EIT 线型可以看成是由两个洛仑兹线型相干叠加而成的。最大透射峰所在位置保持不变，峰值依次下降。最小透射谱宽变窄。相位谱形状保持不变，但最大透射峰值下降，最小透射峰值上升。

2.3 透射率的影响

固定环2 损耗α2和环3 损耗α3，改变透过率t。取α2=0.86，α3=0.99，t 分别取为0.80，0.85和0.90，其透射谱和相位谱的图如图4(a)和图4(b)所示。

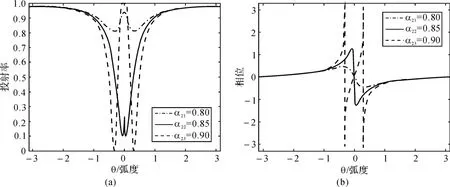
图4 透过率分别对透射谱和相位谱的影响

透射谱都是EIT 线型，随着透过率的增加，最小透射峰值依次下降，最大透射峰所在位置保持不变，峰值先降后升，谱宽先窄后宽。相位谱发生了明显的变化，最大透射峰值从0.2 上升到3。

3 结束语

本文主要从考虑微环间相互作用着手，通过调节环间损耗和透过率来调控单波导双微环耦合系统的透射谱和相位谱。通过研究发现，通过调节环间损耗可以调控EIT 谱两个极值之间的距离。为了获得较好的EIT谱，应该取较大的环3 损耗和透过率。本文研究方法同样也适用于双波导双微环耦合系统的情形。

[1]Harris S E，Field J E，Imamoglu A.Nolinear optical processes using electromagnetically induced transparency[J].Physical Review Letters，1990，64(10):1107-1110.

[2]Yariv A.Universal relations for coupling of optical power between microresonators and dielectric waveguide[J].Electronics Letters，2000，36(4):321-322.

[3]Smith D D，Chang H.Coherence phenomena in coupled optical resonators[J].Journal of Modern optics，2004，5(16):2503-2513.

[4]Liu X，Kong M，Feng H.Transmission and dispersion of coupled double-ring resonators[J].Journal of the Optical Society of America B-Optical Physics，2012，29(1):68-74.

[5]Zhao C Y，Tan W H.Transmission of asymmetric coupling double-ring resonator[J].Journal of Modern Optics，2015，62(4):313-320.

[6]Meng Y C，Guo Q Z，Tan W H，et al.Analytical solutions of coupled-mode equations for multiwaveguide systems obtained by use of Chebyshev and generalized Chebyshev polynomials[J].Journal of the Optical Society of America A，2004，21(8):1518-1527.