基于改进马尔科夫模型的风电系统可靠性评估
胡曹利,占震滨,文成林,高迪驹
(1.杭州电子科技大学系统科学与控制工程研究所,浙江 杭州310018;2.浙江电力调度控制中心,浙江 杭州310000;3.上海海事大学物流工程学院,上海201306)
0 引 言
风能具有清洁、高效等特点,但风能存在间歇性、波动性等缺陷,使得并网风电的波动需要通过常规电源的调节与储能系统来达到平衡,是困扰风电并网的主要难题。大功率和大容量的储能系统能够减小风电的波动性和间歇性,将储能系统与风电机组结合,可以有效抑制风电的波动性和间歇性,减小风电对电网的影响[1]。然而,随着风电机组单机容量和风电场规模的不断扩大,急需研究大型风电场并网给发输电系统带来的影响与风险,全面评估风力发电的价值。在电力系统可靠性评估中,目前采用的主要方法有解析法[2]和蒙特卡罗仿真法[3]。解析法精确度比较高,但其计算量随着系统的规模呈指数关系增长,比较适合于小型电力系统中。蒙特卡罗仿真法原理简单、易于实现,采样次数与系统的规模无关,但需要的样本容量与系统的规模呈指数关系增长,适合风电接入的发输电等大系统的风险分析。本文提出一种利用离散状态马尔科夫链对储能装置充放电过程的建模方法,基于马尔科夫链的平稳分布概率分析系统供电可靠性。在考虑风力发电机组间尾流效应情况下,采用该模型的改进方法对风力发电机组进行仿真,研究尾流效应对系统供电可靠性的影响。
1 风力发电系统的建模
1.1 风机功率特性
根据空气气动力学原理,为了便于推导描述风电机组输出功率波动特性的概率密度函数,用二次模型[4]来近似描述风机的功率输出特性:

式中,Prated为额定功率,Vin为切入风速,Vrated为额定风速,Vout为切出风速。
1.2 风速的随机波动特性
风速随时间的变化可以用概率分布函数来描述。文中选用韦布尔概率密度函数[4]描述风速变化,则概率密度函数为:
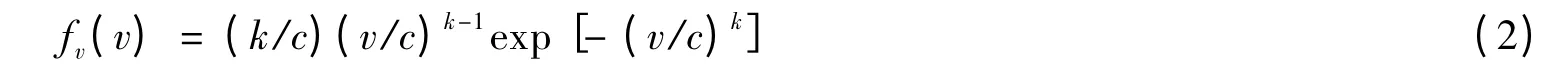
式中,c和k分别为韦伯尔分布的尺度参数和形状参数,v为给定风速(单位为m/s)。
对于风机来说,风吹过地表的风速随海拔高度的变化而变化[4],其规律如下:

式中,v1为在参考高度h1处测量的风速,v2为对高度为h2处风速的估计,a为地表摩擦系数。
1.3 风机输出功率的随机波动特性
由式(1)、式(2)可知,将风机的输出功率分别按照式(1)所分成的3个部分,用式(2)风速的概率密度函数可以求出风机输出功率特性的功率概率密度函数fw(Pw)[5],如下:

式中,δ为Dirac 函数,便于描述功率值在0和Prated处的概率。
2 基于马尔科夫链的可靠性评估
2.1 储能单元电量的随机波动特性
含储能风电系统的供电可靠性不仅取决于风机的输出功率还取决于蓄电池的剩余容量。目前,国内外普遍用荷电状态SOC(State of Charge)[6]来表示蓄电池的剩余容量。
利用安时计数的方法,可以估计出蓄电池的SOC,采用离散时间的表述方法,如下式所示:
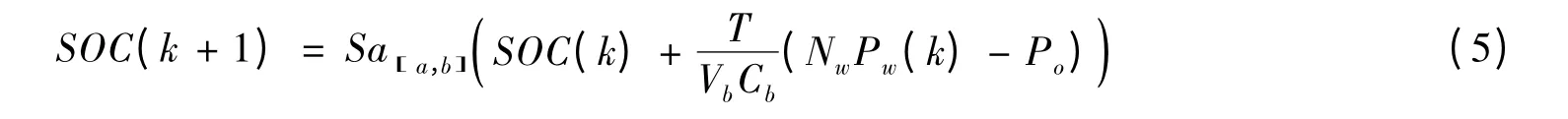
式中,SOC(k),SOC(k+1)分别为第k时刻(即当前时刻)和k+1时刻(即下一时刻)的蓄电池SOC,Nw为风机台数;Pw(t),Po(t)分别为t时刻风机输出功率与负荷的功率需求,Vb,Cb分别为蓄电池的额定电压与额定容量。T表示第k次采样到第k+1次采样的时间采样周期间隔,Sa[a,b](x)为定义的饱和函数。
2.2 蓄电池SOC的马尔科夫模型(DTMC)
由上面可知,蓄电池的SOC(k)可以看作是随机过程。假设不同时刻k的风机输出功率是一组独立同分布的随机变量,则随机过程SOC(k)可以用马尔科夫链来描述。根据马尔科夫链的性质对蓄电池剩余容量随机波动的情况进行分析,进而分析含蓄电池的风机系统载荷能力的概率。因此,建立了风机输出功率分布相同且相互独立的蓄电池SOC的马尔科夫模型(DTMC)[5]。
对于齐次离散时间马尔科夫链SOC,其转移矩阵P的计算如下式所示:
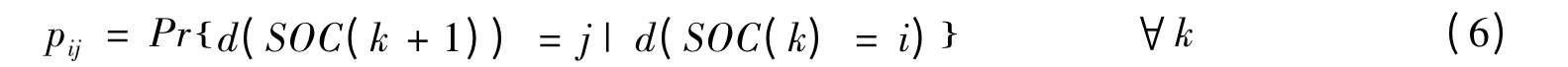
式中,pij为矩阵P 中第i行第j列的元素,表示由状态i 转移到状态j的概率。
fj(x)表示k时刻SOC(k)= x 而k+1时刻d (SOC (k+1))= j的概率,利用式(5)、式(6)得:
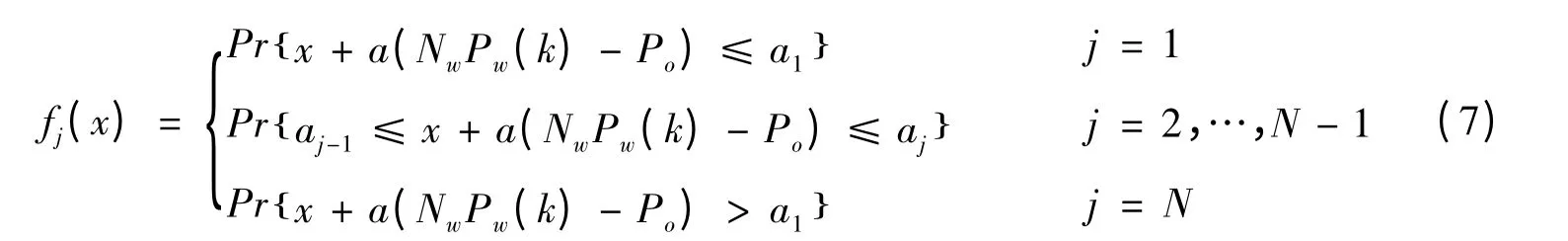

因此,马尔科夫链的状态转移矩阵P的第i行第j列元素pij则可以由下式计算:

2.3 改进的蓄电池SOC的马尔科夫模型
由2.2 节可知,上述建立的蓄电池SOC的马尔科夫模型只能处理风机输出功率分布相同且相互独立的情况。但在实际工作情况下,风力发电机组存在着尾流效应和电器损耗等不确定因素,因此,风机输出功率分布并不是相同且相互独立的,而是相关的。针对这一问题,本文提出一种改进的蓄电池SOC的马尔科夫模型,其能处理风机输出功率相关的情况。
改进的蓄电池SOC的马尔科夫模型为:假设风机的尾流效应和电器损耗等不确定因素对风机Wi的输出功率的损耗率为λi(0 <λi<1,第i 台风机相较于前一台风机),则式(7)改为:
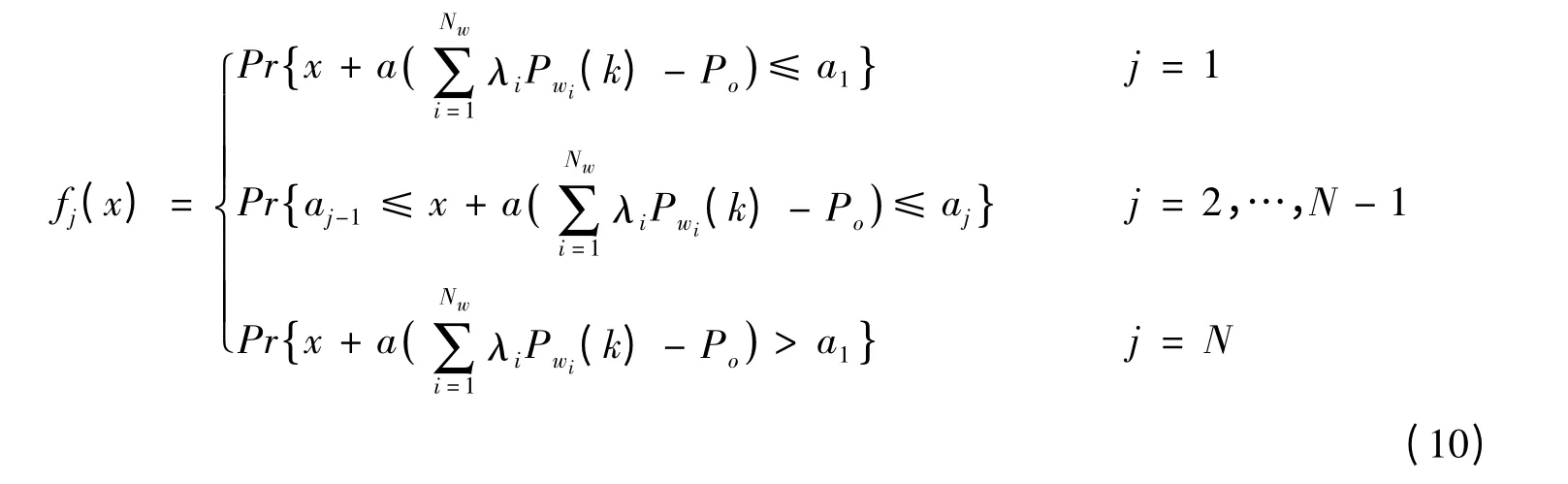
相应的γj(x)改为由式(10)可知,本文改进的蓄电池SOC的马尔科夫模型在2.2 节中介绍的模型的基础上,考虑风力发电机组存在着尾流效应和电器损耗等不确定因素,并根据马尔科夫链的性质对蓄电池剩余容量随机波动的情况进行了分析,进而分析含蓄电池的风机系统的载荷能力,从而进行系统可靠性评估。
3 仿真实验
3.1 实验数据准备
系统备选风机性能参数如表1所示。

表1 系统备选风机性能参数
3.2 仿真结果
3.2.1 海拔高度对风机输出功率的影响
当h1=100 m,h2=1 000 m,a=0.1时,分别得出在不同海拔高度时,风机输出功率的累积概率密度函数随着风速的变化曲线如图1所示。
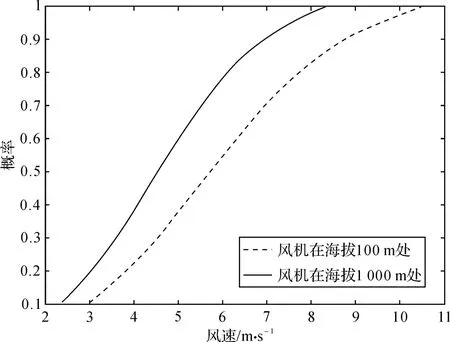
图1 海拔高度对风机输出功率的影响
由图1可看出,海拔高度对风机的输出功率产生较大的影响,海拔越高,风机输出功率越大。
3.2.2 两种模型对系统可靠性评估的比较
假设系统由3 台风机配置4 kAh的蓄电池组成供电系统,负荷的功率需求为400 kW,λi=0.95,蓄电池工作的最大放电深度DOD分别为80%、40%时,系统投入运行蓄电池SOC可能工作在每个离散状态的概率πi分别如表2、表3所示。

表2 DOD=80%时,稳态分布概率值

表3 DOD=40%时,稳态分布概率值
由表2、表3知,风机的尾流效应和电器损耗等不确定因素对风机的输出功率的影响导致了系统可靠性的降低,对电网的供电质量产生不利影响。虽然蓄电池的额定电压、容量大小、型号都一样,但放电深度不同,对系统的供电可靠性也有较大的影响。放电深度越大,系统供电可靠性较高。
相同配置的系统,给定不同损耗率λi=1(风机之间相互独立),λi=0.95(损耗为0.95),λi=0.952,进行MATLAB仿真,仿真结果如图2、图3所示。

图3 不同损耗率跟无损耗率的可靠性概率误差
由图2、图3可知,损耗率越低,系统可靠性越差,其效果随着风机台数的增加而越来越明显。两个图充分显示了风机的尾流效应和电器损耗等不确定因素对风机的输出功率影响很大,继而影响系统的供电质量、运行效率。因此,在实际应用中,不应该认为风机的输出功率是相互独立的。
4 结束语
改进的蓄电池SOC的马尔科夫模型对风力发电系统进行可靠性评估,考虑了风机的尾流效应和电器损耗等不确定因素对风机的输出功率影响,本模型的改进方法更贴切地模拟了风力发电机组在实际工作情况,其结果更能体现系统可靠性的真实情况,可以为含储能系统的设计和风能调度策略的选取提供重要参考。本文中所用的方法可以拓展应用到太阳能发电系统中。
[1]Rabinowitz M.Power systems of the future.4[J].Power Engineering Review,IEEE,2000,20(8):4-9.
[2]赵渊,周家启,周念成,等.电力系统可靠性评估的解析计算模型[J].中国电机工程学报,2006,26(5):19-25.
[3]Salvaderi L,Billinton R.A comparison between two fundamentally different approaches to composite system reliability evaluation[J].Power Apparatus and Systems,IEEE Transactions on,1985,104(12):3486-3492.
[4]杨刚,杜永贤,陈鸣.基于风频Weibull 分布和风机功率特性求解风机发电量[J].电力学报,2008,23(4):276-278.
[5]Li J,Wei W.Probabilistic evaluation of available power of a renewable generation system consisting of wind turbines and storage batteries:A Markov chain method[J].Journal of Renewable and Sustainable Energy,2014,6(1):013139.
[6]Piller S,Perrin M,Jossen A.Methods for state-of-charge determination and their applications[J].Journal of Power Sources,2001,96(1):113-120.

