路、扇及星的Mycielski图的邻点可区别I-全染色
刘秀丽
(菏泽学院 数学系,山东 菏泽274015)
图的染色问题是图论的主要研究内容之一,具有重要的理论意义和现实意义,因而逐渐成为众多学者研究的重要领域之一[1].全染色问题特别是邻点可区别全染色又是染色问题中的难点.2004年,张忠辅等[2]提出了邻点可区别全染色的概念,这个染色问题已经被广泛研究[3-5].在邻点可区别全染色概念的基础上,又提出了图的邻点可区别I-全染色的概念.近年来,一些学者对一些特殊图类的邻点可区别I-全染色进行了研究[6-11],本文讨论了M(Pn),M(Fn)和M(Sn)图的邻点可区别I-全染色,根据M(Pn),M(Fn)和M(Sn)图的特征,给出了一种具体的染色方案,得到了它们的邻点可区别I-全色数,并且满足猜想.
定义1[9,12]对于阶数不小于2的连通图G,f是从V(G)∪E(G)到{1,2,…,k}的映射,k是自然数,如果f满足:
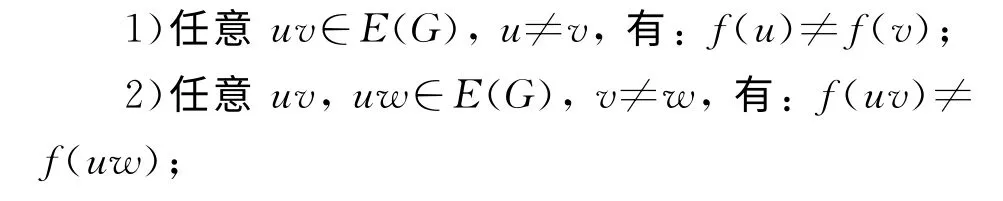
3)任意uv∈EGu≠v有Cu≠Cv.其中C(u)={f(u)}∪{f(uv)|uv∈E(G)},则称f是图G的邻点可区别I-全染色(简记作k-IAVDTC),记χiat(G)=min{k|G有k-邻点可区别I-全染色}为G的邻点可区别I-全色数.
定义2[13-14]设图G是简单图,构造图M(G),使
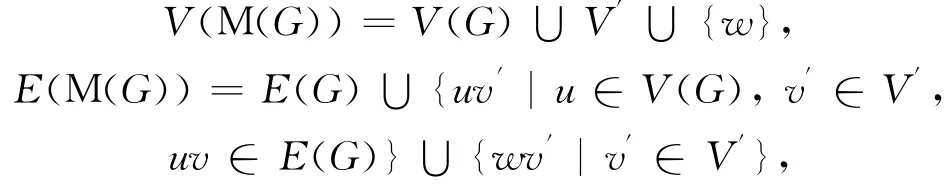
引理1[9]对简单图G,有χi≥Δ.如果任意uv∈E(G)且d(u)=d(v)=Δ,则有χiat(G)≥Δ+1.
猜想1[11]对简单图G,则有χiat(G)≤Δ+2.
本文所讨论的图均为简单、有限图.文中未加说明的记号和术语参见文献[1,15].
1 主要结果及证明
定理1 设Pn表示阶为n(n≥3)的路,则有
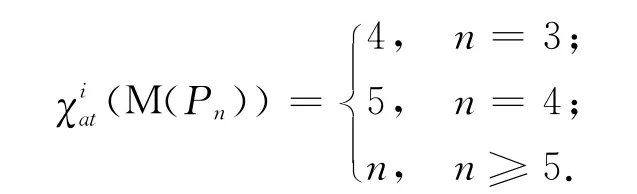
证明 1)n=3.
由图M(P3)的结构知Δ(M(P3))=4,所以由引 理1,有χiat(M(P3))≥4.为 了 证 明χiat(M(P3))=4,只 需 给 出M(F3)的 一 个4-I-AVDTC.为此,构造一个映射f:V(M(P3))∪E(M(P3))→{1,2,3,4}:
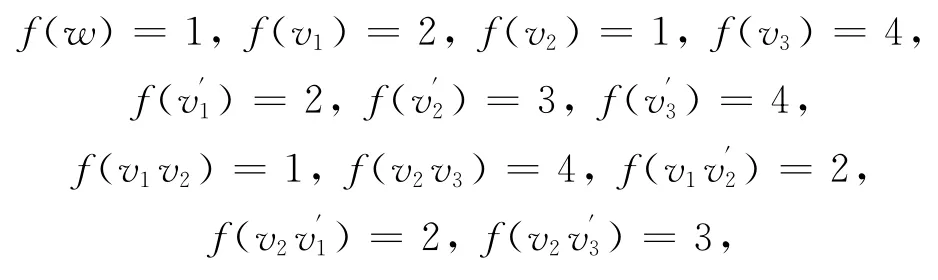
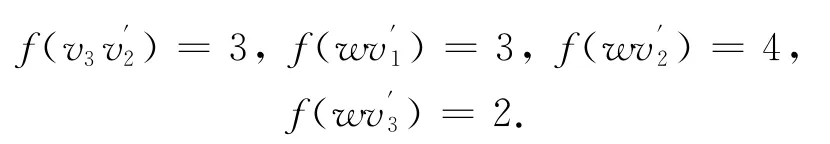
此时
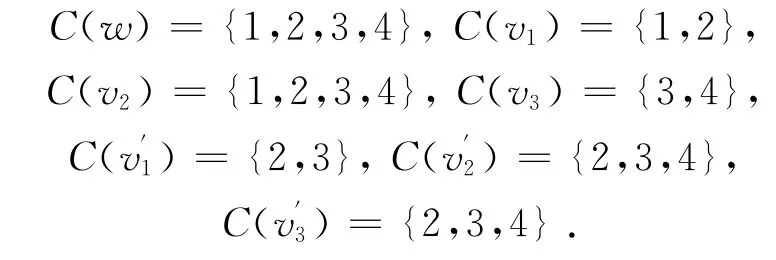
综上,f是M(P3)的一个4-I-AVDTC.所以χiat(M(P3))=4.
2)n=4.
由图M(P4)的结构知Δ(M(P4))=4且最大度点相邻,所以由引理1,有χiat(M(P4))≥5.为了证明χiat(M(P4))=5,只需给出M(P4)的一个5-I-AVDTC.为此,构造一个映射f:
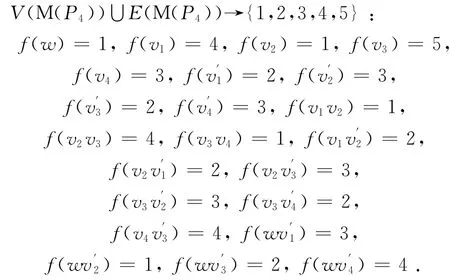
此时
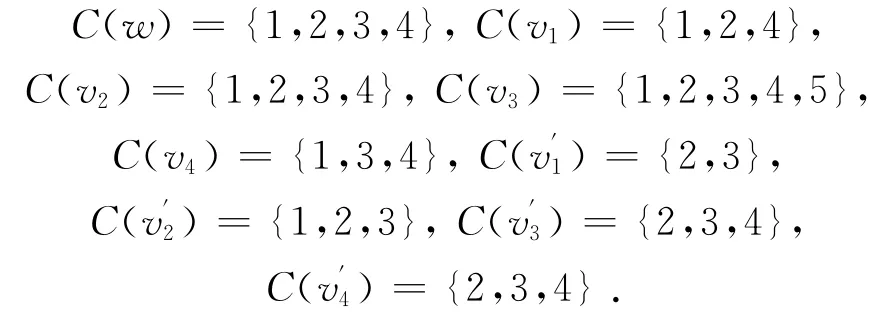
综上,f是M(P4)的一个5-I-AVDTC.所以χiat(M(P4))=5.
3)n≥5.
由图M(Pn)的结构知Δ(M(Pn))=n,所以由引 理1,有χiat(M(Pn))≥n.为 了 证 明只 需 给 出M(Pn)一 个为此,构造一个映射
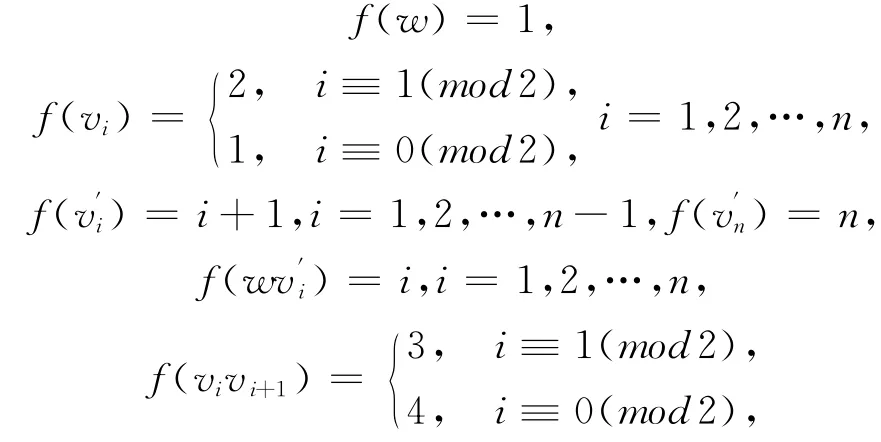
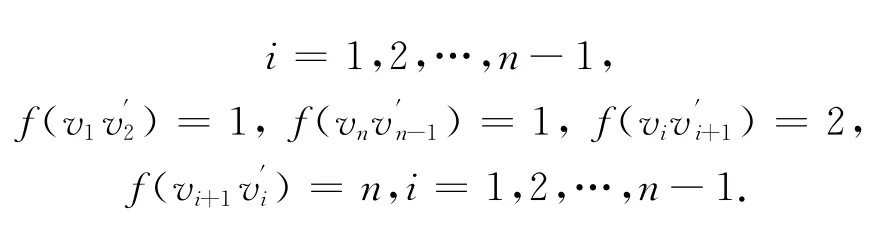
此时
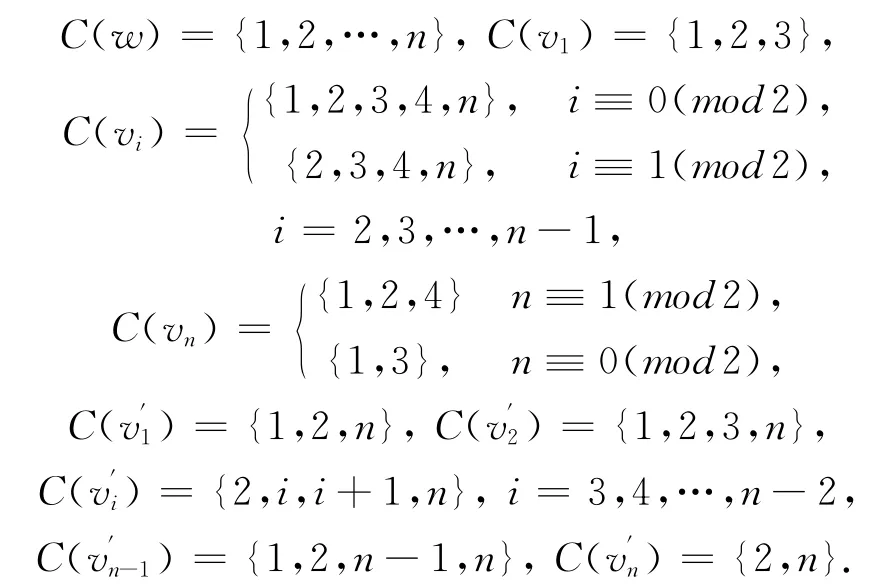
综上,f是M(Pn)的一个n-I-AVDTC.所以χiat(M(Pn))=n.
定理2 设Fn表示阶为n+1(n≥3)的扇,则有
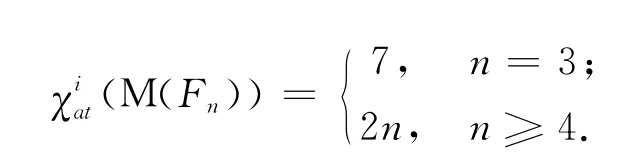
证明 1)n=3.
由图M(F3)的结构知Δ(M(F3))=6且最大度点相邻,所以由引理1,有χiat(M(F3))≥7.不妨设为 了 证 明只 需 给 出M(F3)的一个7-I-AVDTC.为此,构造一个映射f:V(M(F3))∪
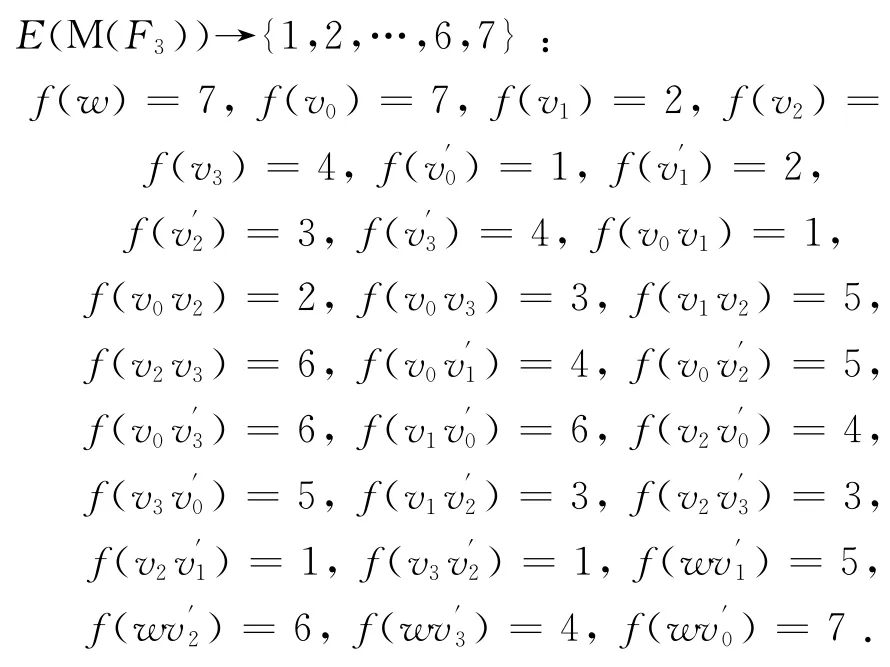
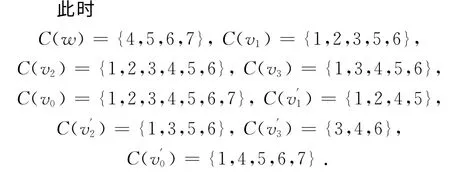
综上,f是M(F3)的一个7-I-AVDTC.
2)n≥4.
由图M(Fn)的结构知Δ(M(Fn))=2n,所以由引理1,有χiat(M(Fn))≥2n.不妨设V(Fn)=为了证明只需给出M(Fn)的一 个2n-I-AVDTC.为此,构造一个映射f:V(M(Fn))∪E(M(Fn))→{1,2,…,2n}:
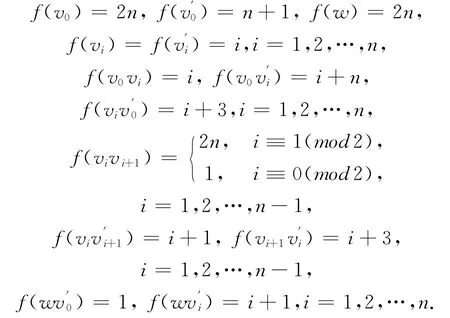
此时

综上,f是M(Fn)的一个2n-I-AVDTC.所以χiat(M(Fn))=2n.
定理3 设Sn表示阶为n+1(n≥3)的星,则有
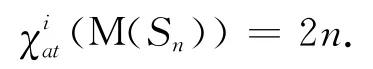
证明 由图M(Sn)的结构知Δ(M(Sn))=2n,所以由引理1,有不妨设为 了 证 明只 需 给 出M(Sn)一 个2n-I-AVDTC.为此,构造一个映射
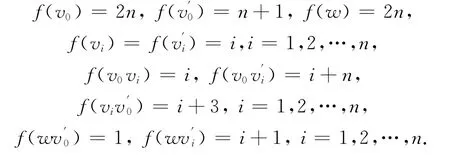
此时
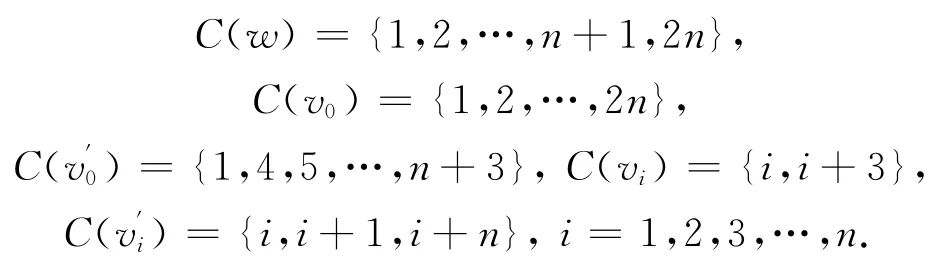
综上,f是M(Sn)的一个2n-I-AVDTC.所以χiat(M(Sn))=2n.
[1]Bondy J A,Murty U S A.Graph theory with apolications[M].London:Macmillan Press Ltd.,1976.
[2]张忠辅,陈祥恩,李敬文,等.关于图的邻点可区别全染色[J].中国科学(A辑),2004,34(5):574-583.Zhang Zhongfu,Chen Xiang'en,Li Jingwen,et al.Adjacent vertex distinguishing total coloring of graph[J].Science in China(Ser.A),2004,34(5):574-583.(in Chinese)
[3]孙晓玲,杜建伟.一类外平面图的邻点可区别全染色[J].中北大学学报(自然科学版),2009,30(1):1-4.Sun Xiaoling,Du Jianwei.Adjacent vertex distinguishing total coloring of a class of outerplane graphs[J].Journal of Nouth University of China(Natural Science Edition),2009,30(1):1-4.(in Chinese)
[4]张芳红,王治文,陈祥恩.C5∨Kt的邻点可区别全色数[J].数学的实践与认识,2012,42(16):247-252.Zhang Fanghong,Wang Zhiwen,Chen Xiang'en.Adjacent-vertex-distinguishing total chromatic numbers of C5∨Kt[J].Mathematics in Practice and Theory,2012,42(16):247-252.(in Chinese)
[5]杨超,姚兵,王宏宇.复合交叉圈的邻点可区别全色数[J].华南师范大学学报(自然科学版),2014,46(1):22-26.Yang Chao,Yao Bing,Wang Hongyu.Adjacent-vertex distinguishing total chromatic numbers of compound intersecting cycles[J].Journal of South China Normal University(Natural Science Edition),2014,46(1):22-26.(in Chinese)
[6]王治文,杨随义,文飞.关于若干倍图的关联邻点可区别全染色[J].内蒙古师范大学学报(自然科学汉文版),2009,38(6):643-646.Wang Zhiwen,Yang Suiyi,Wen Fei.On a number of incidence adjacent vertex-distinguishing total coloring of double graphs[J].Journal of Inner Mongolia Normal University(Natural Science Edition),2009,38(6):643-646.(in Chinese)
[7]杨随义,王治文.一类3-正则图的关联邻点可区别全染色[J].山西大学学报(自然科学版),2010,33(3):354-357.Yang Suiyi,Wang Zhiwen.Incidence adjacent vertexdistinguishing total coloring of a kind of 3-regular graph[J].Journal of Shanxi University(Natural Science Edition),2010,33(3):354-357.(in Chinese)
[8]卢建立,任凤霞,马美琳.项链的若干染色问题[J].科技导报,2012,30(7):44-47.Lu Jianli,Ren Fengxia,Ma Meilin.Several coloring problems involving necklace[J].Science and Technology Review,2012,30(7):44-47.(in Chinese)
[9]杨晓亚.图Pn□Cm的邻点可区别的I-全染色[J].纯粹数学与应用数学,2012,2(6):757-764.Yang Xiaoya.Adjacent vertex-distinguishing I-total colorings of Pn□Cm[J].Pure and Applied Mathematics,2012,2(6):757-764.(in Chinese)
[10]杨随义,高毓平,何万生.图Pm□Kn的邻点可区别I-全染色[J].数学的实践与认识,2013,43(1):212-218.Yang Suiyi,Gao Yuping,He Wansheng.Adjacent vertex-distinguishing I-total coloring of Pm□Kn[J].Mathematics in Practice and Theory,2013,43(1):212-218.(in Chinese)
[11]Chen Xiangen,Gao Yuping,Yao Bing.Not necessarily proper total colourings which are adjacent vertex distinguishing[J].International Journal of Computer Mathematics,2013,90(11):2298-2307.
[12]田京京.冠图Cm·Sn和Cm·Pn的邻点可区别的I-全染色[J].西南师范大学学报(自然科学版),2013,38(2):25-28.Tian Jingjing.On adjacent vertex-distinguishing Itotal chromatic number of the crown graph Cm·Snand Cm·Pn[J].Journal of Southwest China Normal University(Natural Science Edition),2013,38(2):25-28.(in Chinese)
[13]陈祥恩,张忠辅,晏静之,等.关于几类特殊图的Mycielski图的邻点可区别全色数(英文)[J].兰州大学学报(自然科学版),2005,41(2):117-122.Chen Xiang'en,Zhang Zhongfu,Yan Jingzhi,et al.Adjacent-vertex-distinguishing total chromatic numbers on Mycielski's graph of several kinds of pareicular graphs[J].Journal of Lanzhou University(Natural Science),2005,41(2):117-122.(in Chinese)
[14]王继顺.图M(Pn)和M(Cn)的点可区别边色数[J].数学杂志,2012,32(2):363-368.Wang Jishun.Vertex-distinguishing edge chromatic number of M(Pn)and M(Cn)[J].Journal of Math.,2012,32(2):363-368.(in Chinese)
[15]Bollobas B.Modern graph theory[M].New York:Springer-Verlag,1998.

