具有避难所的捕食系统的稳定性
徐国明
(包头师范学院 数学科学学院,内蒙古 包头014030)
避难所作为生物进化过程中食饵种群所采用的有效降低被捕获率的一种策略,受到了广泛的研究.近几年,许多学者研究了具有避难所的捕食者-食饵种群的动力学行为[1-15],在实际生活中,食饵种群为了免于被捕获,常常会到处寻找避难所,在很多情况下存在一个与食饵数量成固定比例的避难所.本文考虑具有避难所的捕食者-食饵系统,其模型为
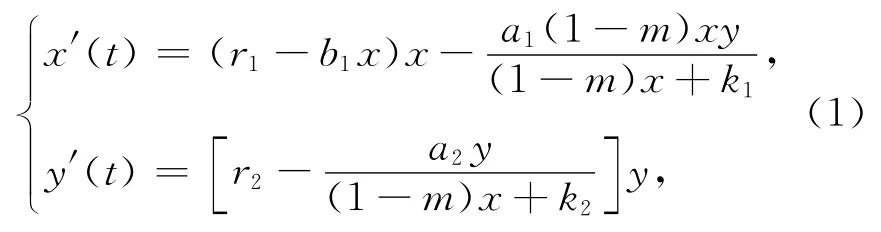
式中:m∈[0,1)是一个常数;mx为避难所保护的食饵数量;(1-m)x为能被捕食者捕获的食饵数量.
1 基本结果
定理1 对任意t≥0,系统(1)满足初始值x(0)>0,y(0)>0的解(x(t),y(t))最终一致有界.
令F(t)=x(t)+y(t),由系统(1)有
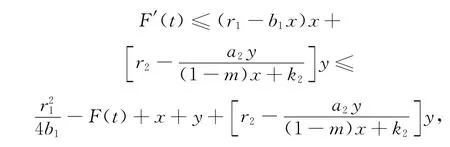
所以
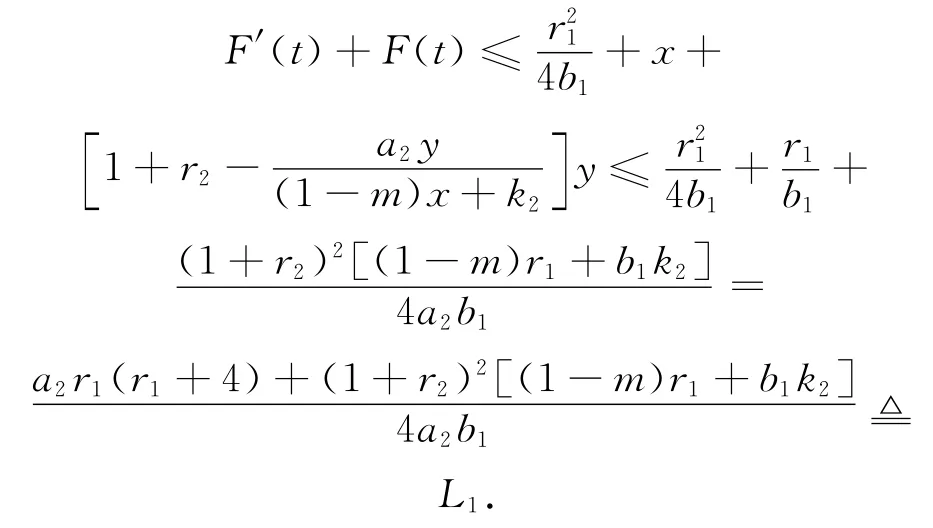
故由比较定理[16]有F(t)≤L1.
显然系 统(1)存 在 三 个 平 衡 点E1(0,0),令
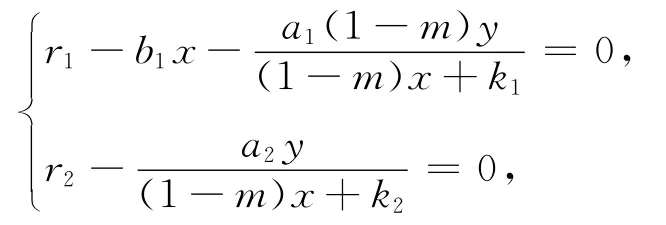

定理2 平衡点E1(0,0)是不稳定的结点;当时,平衡点是局部渐近稳定的;平衡点是鞍点;当r1≤r2且时,正平衡点E4(x0,y0)是局部渐近稳定的.
证明 系统(1)在任意平衡点(x*,y*)处的Jacobian矩阵为

对于平衡点E1(0,0),其特征方程为(λ-r1)(λ-r2)=0,故特征根为λ1=r1>0,λ2=r2>0,所以E1(0,0)是不稳定的结点.
系统(1)在正平衡点E4(x0,y0)处的Jacobian矩阵为
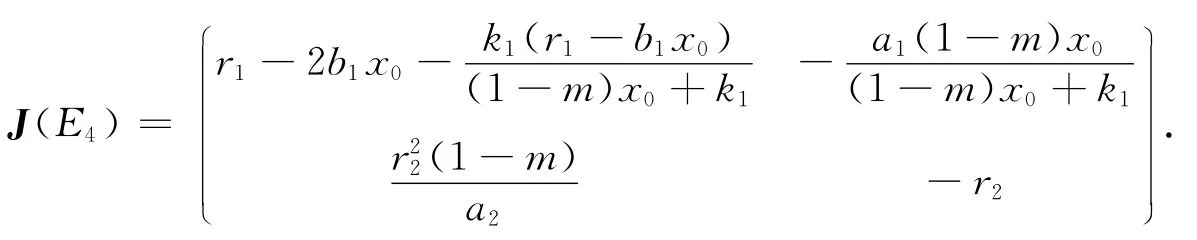
故

则当r1≤r2且m>1-时,有J(E4)两个负的特征根,所以此时正平衡点E4(x0,y0)是局部渐近稳定的.
证明 构造Lyapunov函数

显然,对任意的x>0,y>0,V(x,y)有定义且连续,且有
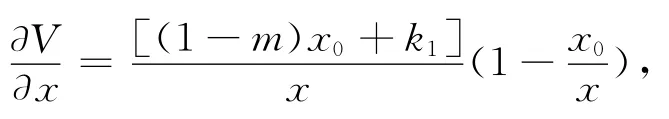
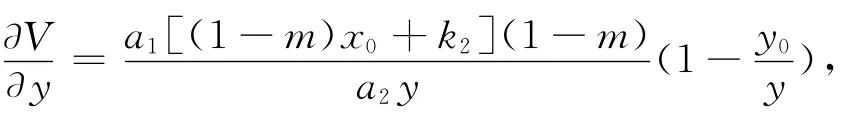
则正平衡点E4(x0,y0)是函数V(x,y)唯一的正极值点,且有

故平衡点E4(x0,y0)为V(x,y)的最小值点,即对任意的x>0,y>0,有
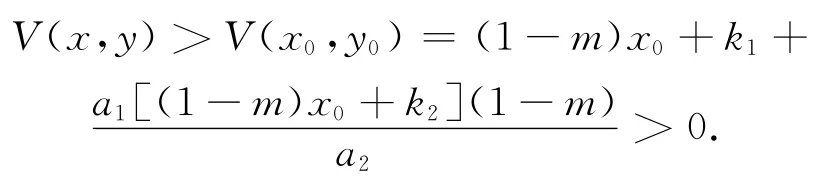
下面计算V(x,y)沿系统(1)的导数
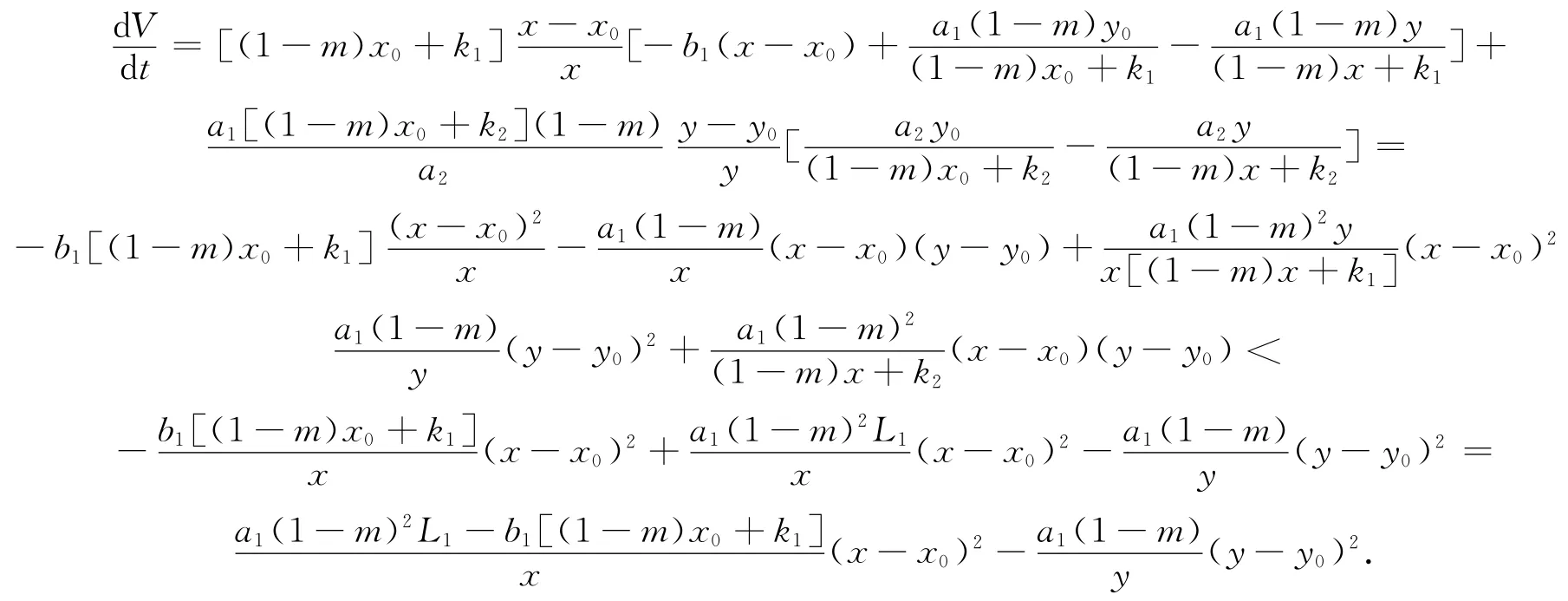
2 结论及实例
通过上面的分析可以发现,系统(1)中的食饵种群和捕食者种群不能同时灭绝,也不可能出现食饵种群持续生存而捕食者种群走向灭绝的现象.同时发现,避难所的容量影响系统的稳定性.令则当m<m0时,食饵种群灭绝;当m>m0时,两种群共存.作为主要结论的一个应用,令
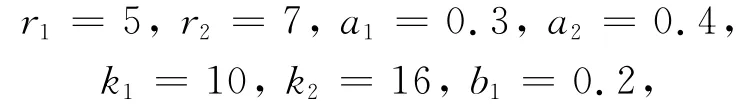
则系统(1)化为
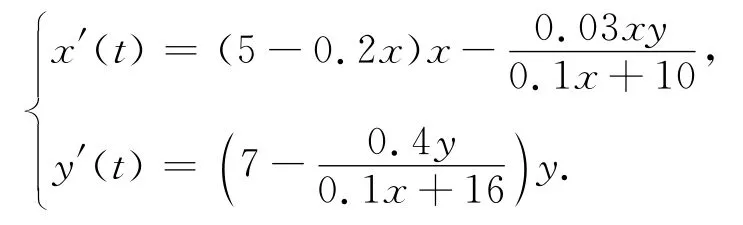
若令m=0.9,经计算
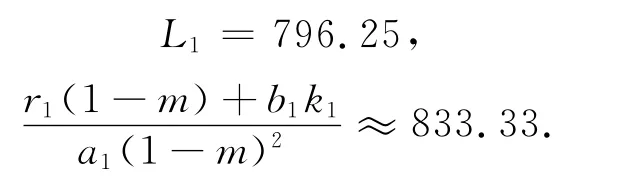
故正平衡点Er(x0,y0)是全局渐近稳定的.
[1]Collings J B.Bifurcation and stability analysis of a temperature dependent mite predator-prey interaction model incorporating a prey refuge[J].Bulletin of Mathematical Biology,1995,57(1):63-76.
[2]Kar T K.Stability analysis of a prey-predator model incorporating a prey refuge[J].Communications in Nonlinear Science and Numerical Simulation,2005,10(6):681-691.
[3]Kar T K.Modelling and analysis of a harvested preypredator system incorporating a prey refuge[J].Journal of Computational and Applied Mathematics,2006,185(1):19-33.
[4]Ko W,Ryu K.Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a prey refuge[J].Journal of Differential Equations,2006,231(2):534-550.
[5]Huang Yunjin,Chen Fengde,Li Zhong.Stability analysis of a prey-predator model with Holling type III response function incorporating a prey refuge[J].Applied Math.and Computation,2006,182(1):672-683.
[6]Chen Fengde,Chen Liujuan,Xie Xiangdong.On a Leslie-Gower predator-prey model incorporating a prey refuge[J].Nonlinear Analysis:Real World Applications,2009,10(2):2905-2908.
[7]Cressman R,Garay J.A.Predator-prey refuge system:evolutionary stability in ecological systems[J].Theoretical Population Biology,2009,76(4):248-257.
[8]Chen Liujuan,Chen Fengde,Chen Lijuan.Qualitative analysis of a predator-prey model with Holling type II functional response incorporating a constant prey refuge[J].Nonlinear Analysis:Real World Applications.2010,11(1):246-252.
[9]Liu Xia,Han Maoan.Chaos and Hopf bifurcation analysis for a two species predator-prey system with prey refuge and diffusion[J].Nonlinear Analysis:Real World Applications,2011,12(2):1047-1061.
[10]Mukhopadhyay B,Bhattacharyya R.Effects of deterministic and random refuge in a prey-predator model with parasite infection[J].Mathematical Biosciences,2012,239(1):124-130.
[11]Yang Wensheng.Diffusion has no influence on the global asymptotical stability of the Lotka-Volterra prey-predator model incorporating a constant number of prey refuges[J].Applied Mathematics and Computation,2013,223(15):278-280.
[12]Jana D.Chaotic dynamics of a discrete predator-prey system with prey refuge[J].Applied Mathematics and Computation,2013,224(1):848-865.
[13]陈柳娟,陈凤德.避难所对一类阶段结构捕食-食饵模型的影响[J].福州大学学报(自然科学版),2013,41(3):283-290.Chen Liujuan,Chen Fengde.The influence of refuge on a stage-structured predator-prey model[J].Journal of Fuzhou University(Natural Science Edition),2013,41(3):283-290.(in Chinese)
[14]郭瑜婷,魏凤英.具有避难所和修正Leslie-Gower项的捕食者-食饵模型的最优税收[J].福州大学学报(自然科学版),2013,41(2):132-136.Guo Yuting,Wei Fengying.Optimal taxation of predator-prey model with a prey refuge and modified Leslie-Gower term[J].Journal of Fuzhou University(Natural Science Edition),2013,41(2):132-136.(in Chinese)
[15]龚晓杰,陈凤德,杨坤,等.具有避难所和捕获的非线性模型稳定性分析[J].龙岩学院学报,2014,32(2):10-14.Gong Xiaojie,Chen Fengde,Yang Kun,et al.Stability of a nonlinear competition model Incorporating a costant proportion of refuge for one species and harvesting[J].Journal of Longyan University,2014,32(2):10-14.(in Chinese)
[16]马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2001.
[17]马知恩.种群生态学的数学建模与研究[M].合肥:安徽教育出版社,1996.

