Pascal函数矩阵的进一步推广及应用*

赵熙强，李 琳

（中国海洋大学数学科学学院，山东 青岛 266100）

n＋1阶Pascal矩阵Pn与n＋1阶Pascal函数矩阵Pn［x］分别定义为［1］：

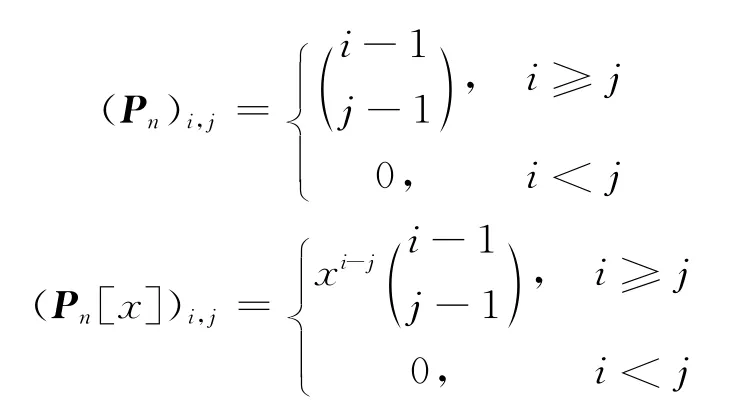
其中：i，j＝1，2，…，n＋1，文献 ［1-6］讨论了Pn与Pn［x］的性质及应用，文献［1］研究了Pn［x］的逆，文献［2-3］分别研究了Pn与Pn［x］的分解问题，文献［4］利用Pn给出了两类Stirling矩阵的分解，文献［5-6］研究了Pn与Fibonacci矩阵之间的关系，并通过矩阵展开式得到了一些组合恒等式，而在文献［7-11］中，分别给出并研究了Pn［x］不同的推广形式。本文将在以上研究的基础上对Pascal函数矩阵再作进一步的推广并讨论其代数性质及应用。

1 定义及性质

定义1.1 设f（t）为t的n阶可导函数，n＋1阶下三角矩阵Pn［f（t）］定义为

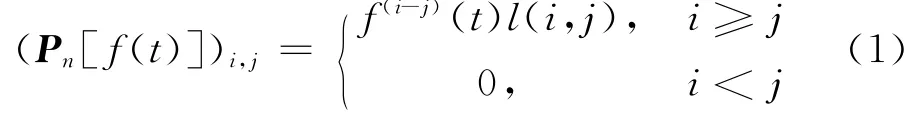
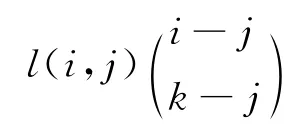
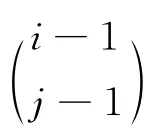
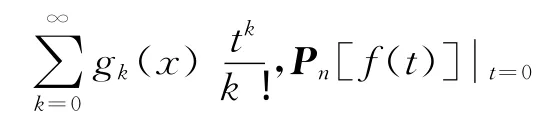
由此可见，定义1.1是文献［7-11］中Pascal函数矩阵的推广形式，下面将给出Pn［f（t）］的一些性质。

定理1.1Pn［f（t）］Pn［g（t）］＝Pn［f（t）g（t）］。

证明 由于Pn［f（t）］与Pn［g（t）］均为下三角矩阵，所以 当i＜j时， （Pn［f（t）］Pn［g（t）］）i，j＝（Pn［f（t）g（t）］）i，j＝0；当i≥j时，由矩阵乘法规则，得

结论成立。

推论1.2 若（f（t）－1）（k）存在，其中k＝0，1，…，n，则

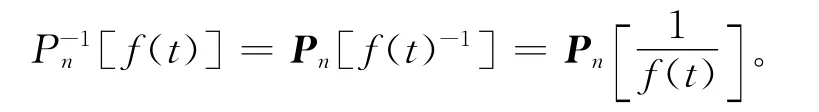
证明 由定理1.1，Pn［f（t）］Pn［f（t）－1］＝Pn［f（t）f（t）－1］＝Pn［1］＝In＋1，

其中：In＋1为n＋1阶单位矩阵，因此结论成立。

｛an｝，｛bn｝为2个任意序列，由推论1.2可得以下反演关系：

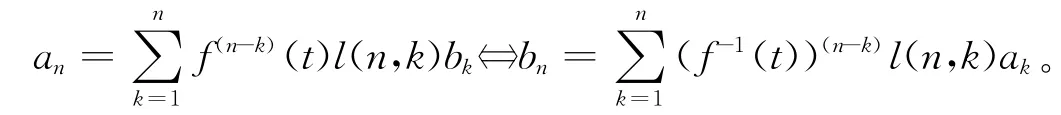
将f（t）＝et代入上式，并令t＝0，得

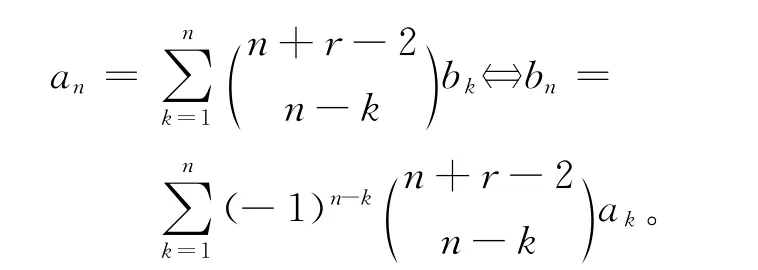
上式中r＝1时，即得到著名的二项式反演公式：

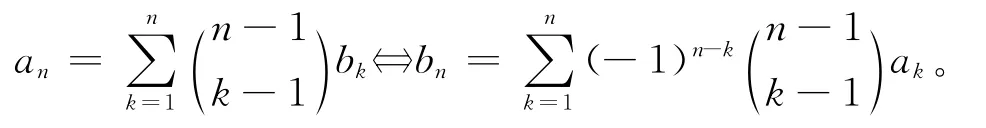
定理1.3a，b为2个任意实数，f（t），g（t）为2个n阶可导函数，则

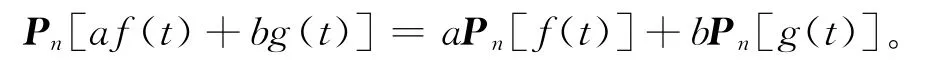
证明 （aPn［f（t）］＋bPn［g（t）］）i，j＝a（Pn［f（t）］）i，j＋b（Pn［g（t）］）i，j＝af（i－j）（t）l（i，j）＋bg（i－j）（t）l（i，j）＝（af（t）＋bg（t））（i－j）l（i，j）＝（Pn［af（t）＋bg（t）］）i，j。结论成立。

定理1.4n为正整数，Pn［f（t）］定义如（1）式，则

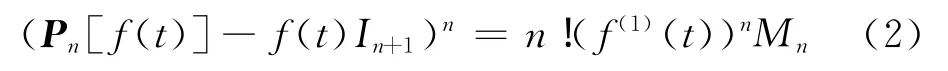
其中：Mn为n＋1阶矩阵，除（Mn）n＋1，1＝l（n＋1，1）外，其余元素为0。

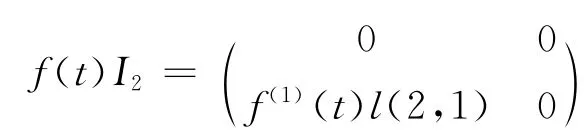
比较上式2边的对应元素，可得以下推论。

推论1.5

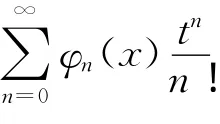
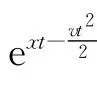
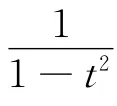
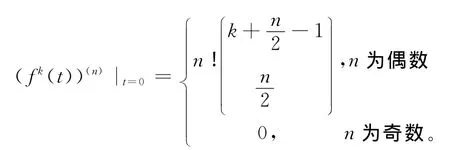
将f（t）代入（3）式和（4）式，并令t＝0，得

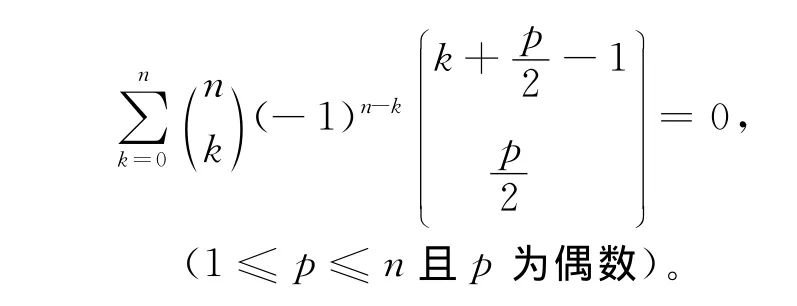
在数码时代的实际生活中，因为以马赛克形式的超文本存在，加上赛博格化赋予其生命，照片能够轻易地与其他媒介交互融合，社会性使用爆炸式拓宽了。里奇详细列举说：

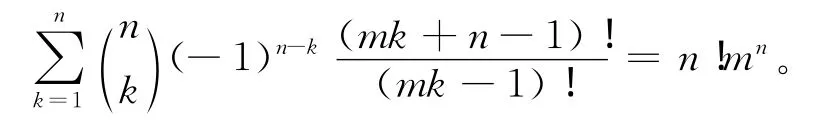
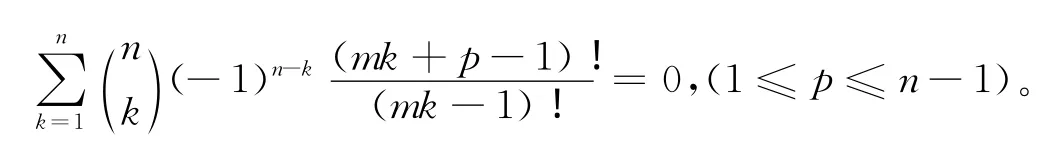
当m＝1时，有

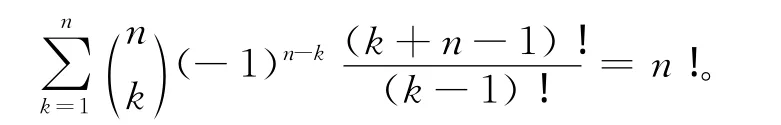
2 Pn［f（t）］的展开式

设n＋1阶方阵Mk除（k＋i，i）（i＝1，2，…，n＋1－k）处的值为l（k＋i，i）外，其余值均为0，（k＝1，2，…，n），由文献［9］，Mk满足以下性质

定 理 2.1Pn［f（t）］＝f（t）In＋1＋f（1）（t）M1＋f（2）（t）M2＋ … ＋f（n）（t）Mn。

证明

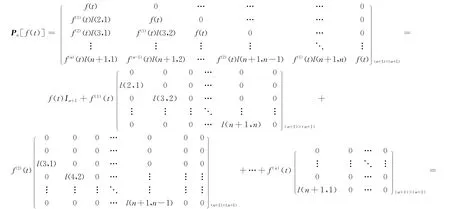
f（t）In＋1＋f（1）（t）M1＋f（2）（t）M2＋ … ＋f（n）（t）Mn， 结论成立。

令M1＝M，由（5）式，得

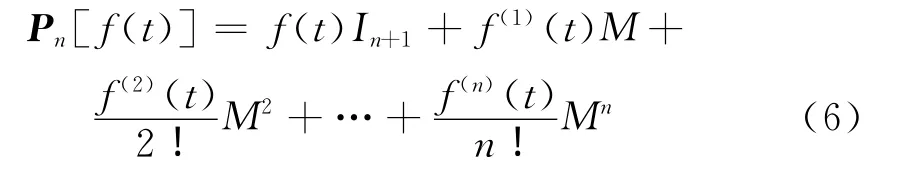
推论2.2

（1）M与Pn［f（t）］的乘积可交换；

（2）（Pn［f（t）］－f（t）In＋1）n＋1＝0；

（3）（Pn［f（t）］－f（t）In＋1）n＝n！（f（1）（t））nMn；

（4）（Pn［f（t）］－f（t）In＋1－f（1）（t）M）n－1＝0，（n≥3）。

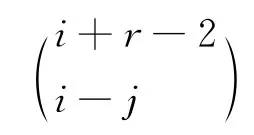
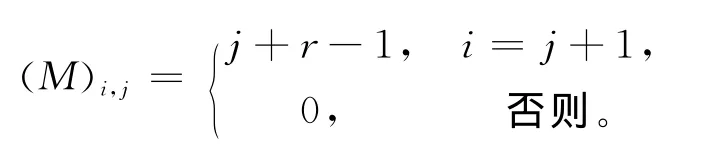
将f（t），l（i，j）代入（6）式，并令t＝0，即得文献［11］中的定理2.5。

3 Pn［f（t）］的2个推广

定义3.1 设f（t），g（t），h（t）为t的n阶可导函数＝｛an｝n≥0＝｛bn｝n≥0为2个任意序列，分别定义矩阵如下：

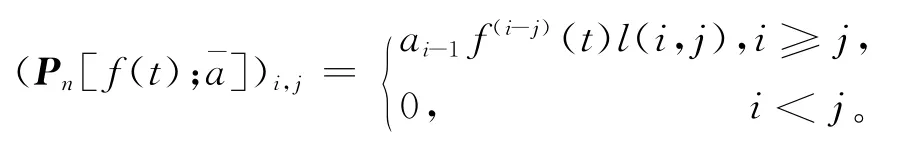
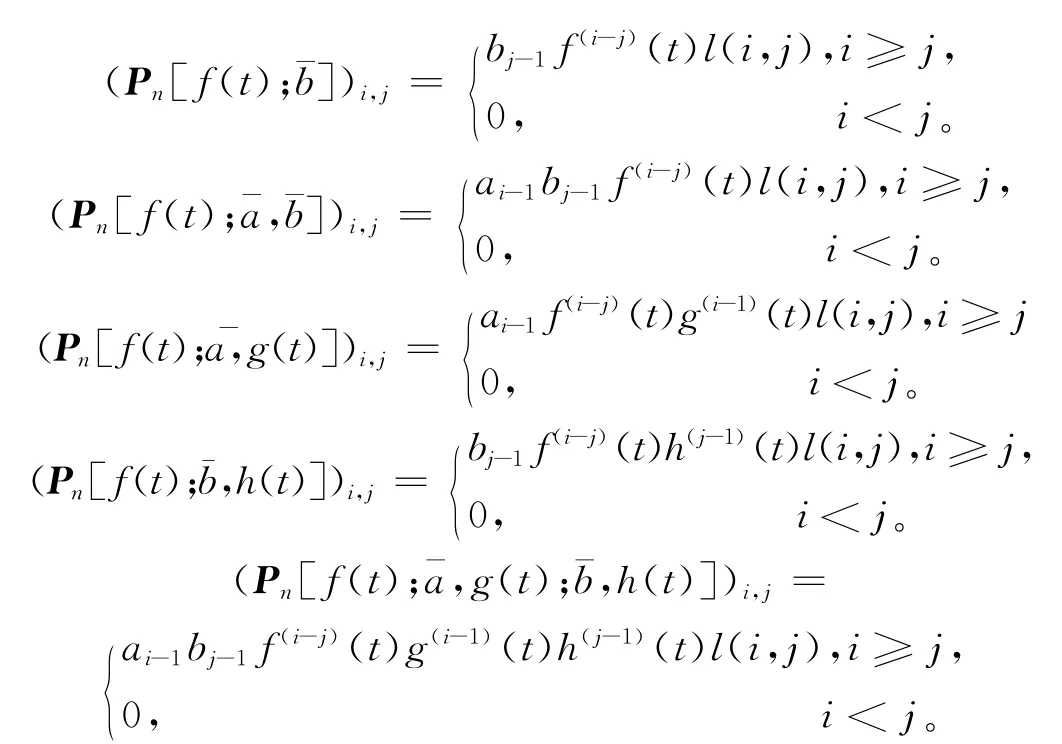
由定义3.1可得以下引理与定理。

引理3.1

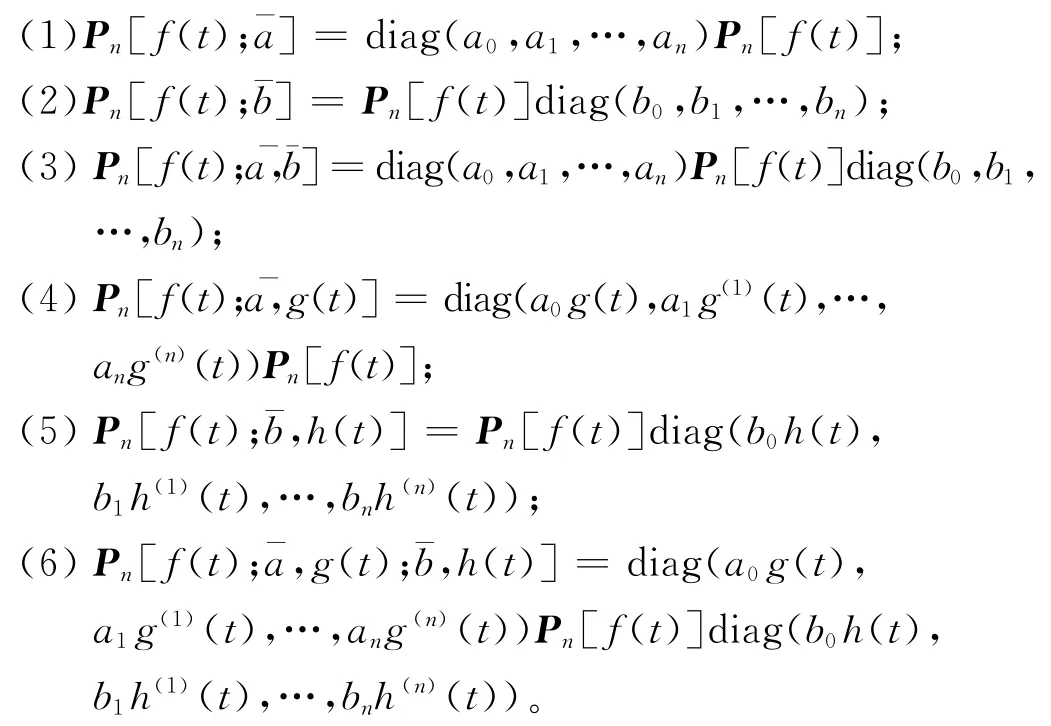
引理3.1的结论可由矩阵乘法运算得到，可请读者自行验证。

定理3.2

证明 定理3.2可由引理3.1和定理1.1得到，现以证明结论（1）和（3）为例，其它结论的证明类似，可由读者自己证明。

证明（1）：

证明（3）：

定义3.2 设f（t）为t的n阶可导函数，y为任意实数，n＋1阶矩阵Pn［f（t），y］定义为

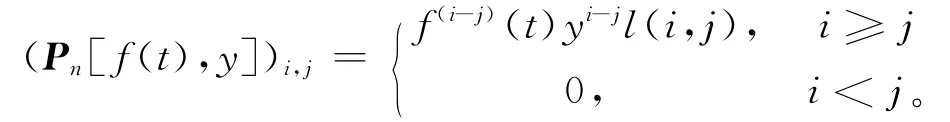
定理3.3 设f（t），g（t）为t的n阶可导函数，y，z为任意实数，m为正整数，则

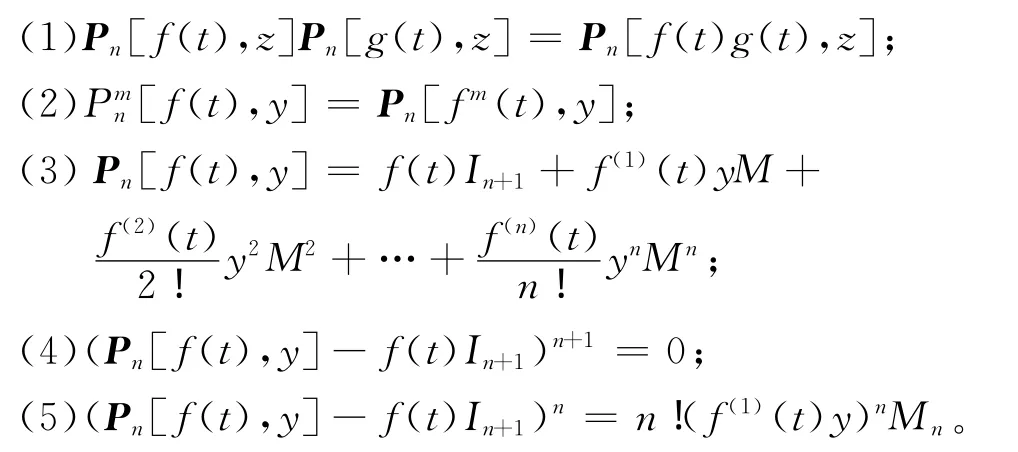
其中：（1）和（3）的证明分别同定理1.1和定理2.1，（2）由（1）归纳得到，（4）、（5）可由（3）得到，（5）还可由定理1.4中的方法来证明。

4 结语

本文对Pascal函数矩阵作了进一步的推广，研究了其代数性质及其在寻找组合恒等式与反演关系方面的应用，给出了推广的Pascal函数矩阵Pn［f（t）］的展开式，相信其在矩阵分解方面会有重要的应用，最后给出了Pn［f（t）］的2个推广及若干定理。

［1］CallG S，Velleman D J.Pascal′s matrices［J］.Amer Math Monthly，1993，100：372-376.

［2］Brawer R，Pirovno M.The linear algebra of the Pascal matrix［J］.Linear Algebra Appl，1992，174：13-23.

［3］Zhang Z Z.The linear algebra of the generalized Pascal matrix［J］.Linear Algebra Appl，1997，250：51-60.

［4］CheonGi-Sang，Kim Jin-Soo.Stirling matrix via Pascal matrix［J］.Linear Algebra Appl，2001，329：49-59.

［5］LeeGwang-Yeon，Kim Jin-Soo，Cho Seong-Hoon.Some combina-torial identities via Fibonacci numbers［J］.Discrete Appl.Math，2003，130：527-534.

［6］Zhang Z Z，Wang X.A factorization of the symmetric Pascal matrix involving the Fibonacci matrix ［J］.Discrete Appl Math，2007，155：2371-2376.

［7］Bayat M，Teimoori H.The linear algebra of the generalized Pascal functional matrix［J］.Linear Algebra Appl，1999，295：81-89.

［8］Zhao X.Q，Wang T.M.The algebraic properties of the generalized Pascal functional matrices associated with the exponential families［J］.Linear Algebra Appl，2000，318：45-52.

［9］谭明术，王天明.具有二项式型多项式下三角矩阵的性质 ［J］.数学研究与评论，2005，25（1）：183-190.

［10］Yang Y Z，Micek C.Generalized Pascal functional matrix and its applications［J］.Linear Algebra Appl，2007，423：230-245.

［11］Stefan，S.A generalization of the pascal matrix and its properties［J］. Factauniversitatis-series：Mathematics and Informatics，2011，26：17-27.

［12］Yang S L.Some identities involving the binomial sequences［J］.Discrete Math，2008，308：51-58.