高频地波雷达海杂波抑制的时频－矩阵联合法*

王祎鸣，张 杰，纪永刚，于长军，毛兴鹏

（1.国家海洋局第一海洋研究所，山东 青岛 266061；2.哈尔滨工业大学，黑龙江 哈尔滨 150001；3.海洋遥测工程技术研究中心（国家海洋局与航天科技集团共建），山东 青岛 266061）

高频地波雷达具有探测距离远、范围广、持续性强等特点，已成为海洋遥感、遥测的一种重要手段。其利用高频电磁波沿海面绕射传播的原理，能检测到海平面视距以外的船只与低空飞机等目标。但是，作为传播媒介的海洋中始终存在与雷达波长尺度相近的海浪，在谐振作用下叠加产生很强的回波。同时，由于海水运动和雷达体制等原因导致了这种回波的能量具有一定程度的拓展。对于CFAR（Constant False Alarm Rate）等基于阈值门限的海面目标检测，相当于在更大的范围内抬高了检测基底，导致杂波被误检为船只目标，而部分船只无法被测出，造成了虚警与漏警现象。相比于雷电、电台及电离层杂波等干扰，这种影响的持续性更强，空间跨度更大。作为一种严重制约高频雷达海面目标探测能力的主要干扰［1－2］，海杂波的有效抑制成为高频雷达领域的重要问题。

海杂波抑制需要考虑两个关键方面：一是保持目标特性，避免有效信号在处理域内的损失，提高信杂噪比；二是杂波抑制手段应为后续的信号与数据处理保留更多信息提取的自由度。高频超视距雷达海杂波抑制有对消法［3－4］、线性预测法［5］、图像处理法［6］以及奇异值分解法［7－8］等。其中迭代对消法需要对表征海杂波的复正弦信号的幅度、频率和初相进行精确估计，否则将致使杂波剩余和扩散，性能也会急剧恶化；线性预测法中的参数估计复杂度高，适应性不强；图像处理法在去除海杂波的同时，回波局部特征易受破坏；而基于奇异值分解的方法可以从雷达回波信号中有选择性的去除杂波分量，在避免上述问题的同时，能最大程度上提高信杂噪比。文献［9］对此类方法进行了比较，指出其还具有对海杂波相关性要求低，不需高维求逆等大运算量计算等优点，但存在的问题是难以准确估计杂波奇异值，导致处理效果的下降。

本文将利用时频分析与矩阵分解所得信息，提出一种新的海杂波抑制方法。首先，针对高频地波雷达的特点，分析海杂波信号的频率、幅度以及时频特性；然后，通过海杂波信号统计模型与高频雷达回波状态方程表明海杂波及船只信号的频率变化可在此基础上进行估计，结合杂波特性提出时频－矩阵联合的海杂波抑制方法；最后，采用实测数据验证该方法的有效性。

1 高频海杂波特性分析

1.1 海杂波频率

高频地波雷达对海探测期间，沿海面传播的电磁波与其波长尺度相近的海浪作用发生Bragg散射，在回波频谱中表现为一阶Bragg峰及二阶连续谱。谐振产生的一阶峰幅度通常远强于连续谱，成为船只检测应用中海杂波的主要成分。一阶峰［10］由2个对称于零频的尖峰构成，多普勒频移的理论值为：

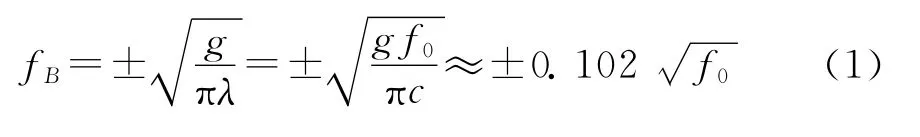
式中：fB为布拉格频率；f0为雷达工作频率。

当海流存在时，海浪叠加到运动的海面，引起多普勒谱中的2个布拉格尖峰朝同一方向等量偏移［11－12］。由海杂波的这种频谱性质可知正负布拉格频率理论位置虽有所偏离，但是频率间隔相对固定，即2fB，这是海杂波的显著频率特性。

1.2 海杂波幅度

海洋是一个不断变化的动态系统，雷达观测到的回波能量随波浪的运动产生变化［13］。海杂波谱主要与雷达工作频率和海态（风速、风向）有关，根据Barrick［14］的一阶和二阶雷达散射截面方程进行数值模拟，仿真计算出雷达工作频率为8.9MHz，4级风速，风向为90°，45°以及20°时各多普勒频率的海浪散射系数。图1中的多普勒频率以海杂波峰值点为准进行了归一化，风向为海面风与产生谐振海浪的夹角。可见，单由风向改变，海杂波幅度就可发生较大的波动。

图1 不同风向条件下的海浪散射系数Fig.1 Wave scattering coefficients under different wind direction

1.3 海杂波的时频表征

为获得有利于船只检测的信噪比，高频地波雷达相干处理的积累时间通常达数分钟。传统的二次傅立叶处理过程，相当于在此期间对回波进行平均处理；而海面处于连续的运动状态，海水波动频率也随之缓慢改变［15］，长时间的积累不能准确反映海杂波幅度与频率的变化情况。

因此，需采用时频分析的技术手段，描述信号频谱含量相对于时间的变化。通过建立时变频谱的分布，方便在时间和频率上同时表示信号的局部化信息及能量分布［16］。图2为实测高频地波雷达海杂波信号的时频分布。图中2条横向的亮线分别对应于正负一阶Bragg峰。

由图2可见，使用时频分析的方法观测时变海面对高频电磁波的作用，反映出海面回波的更多有效信息：

（1）实测海杂波多普勒频率的位置较理论公式（1）计算得到的fB＝±0.304 3Hz，产生同向偏移，但峰值频率间距保持相对固定。据高频海洋遥感反演原理，表明海面存在径向流且远离雷达接收站。

（2）海杂波能量分布是随频率变化的，其能量在几十秒的时间内呈现较强连续性且伴随有强弱交替，这是由海面回波的相干性以及海面风向与雷达波束夹角的改变所致。

（3）海杂波频谱能量主要集中于10－2Hz量级的频率范围内。从趋势看，携带主要能量的海杂波频率变化并不剧烈（时间窗口为30s）。

图2 高频雷达海杂波时频分布Fig.2 Time-frequency distribution of sea clutter

2 海杂波信号模型及抑制方法

2.1 海杂波信号模型

海浪可被看作是由各个波长的正弦波叠加形成，高频雷达海浪回波主成分服从高斯分布，其所对应的回波多普勒频谱幅度符合瑞利分布。经数字化采样的一阶海杂波通常可用复正弦信号模拟［17］，即

其中：n＝0，1，…，N－1为时间采样点数；Ts为采样间隔；fp（n），fn（n）为正负多普勒频率；A（n），A′（n）为满足高斯分布的振幅。

船只等目标回波，同样可以用复正弦信号模型化；高频地波雷达接收的海面回波信号可表示为雷达分辨单元内海浪与船只回波的叠加，即

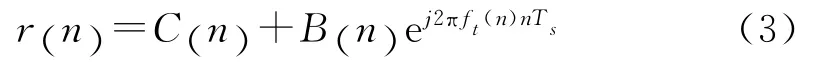
其中：B（n），ft（n）分别为船只目标的幅度和频率。

因此，回波信号中将含有多个有效频率分量。通常情况下，海杂波及船只的频率在一定的时间内变化缓慢，可将接收信号建模为振荡器的输出。状态空间模型［5］为

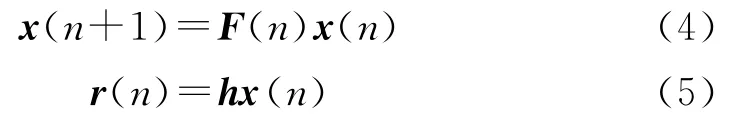
其中：x（n）为状态向量；F（n）为状态反馈矩阵；h为输出向量。

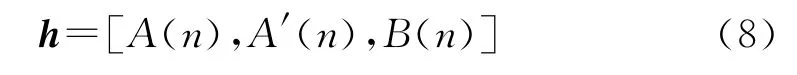
据方程（4）和（5），通过最小二乘法可得到状态反馈矩阵［18］，进而得到雷达回波信号分量的瞬时频率w1、w2及w3。由海杂波信号统计模型与雷达回波状态方程表明，海杂波及船只信号的频率变化可在此基础上进行估计。

2.2 海杂波抑制方法

海杂波抑制是一个将杂波分量从复合回波中剔除的过程。利用海杂波在时频域分析中表现出的特征，结合信号各分量的瞬时频率估计算法，从矩阵构造与时频域联合的角度进行海杂波的抑制。

首先采用矩阵分解的方法，如SVD（Sigular Value Decomposition），通过对特定奇异值置零，移除相对应的特征向量。将高频雷达回波信号分段构造成长方阵，对N点时域采样数据y（n），以Hankel矩阵的形式表示，即：

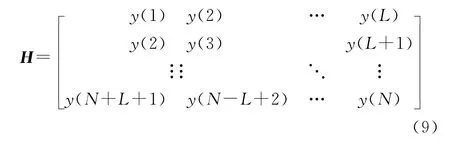
其中：L≥3r；r为数据所含的慢时变信号分量个数，即海杂波与船只回波的数量。

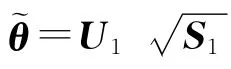
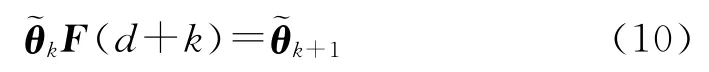
式中：d为L的中值；F（d＋k）为状态反馈矩阵，写作

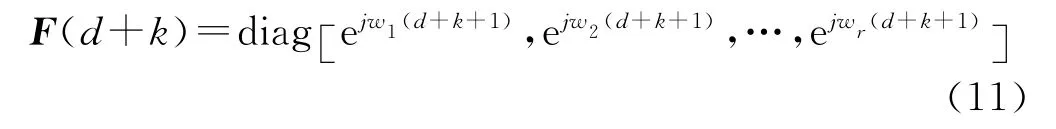
该状态反馈矩阵可由方程（10）用最小二乘法获解，信号分量的瞬时频率可根据矩阵特征值的相位角估计获得。

短时傅立叶变换（STFT）作为一种经典的时频分析方法，可通过窗函数的选择，获取不同的时间分辨率和频率分辨率。数字信号x（n）的STFT表达式为

式中：k＝0，1，…，M－1，M为傅立叶点数；N为窗函数g的步长。

海杂波信号波形变化较为平缓，即低频信息较多，分析窗口可适当延长，获取较长的时间采样，提高频率分辨率。将变换值求平方，得到采样数据的功率谱。

利用海杂波特性，尤其是在时频域所表现出的特征，可以进一步确定回波信号中海杂波分量随时间及频率的变化。将降秩SVD方法所得到的主分量奇异值与估计的瞬时频率相匹配，实现海杂波奇异值的判别。反推海杂波奇异值并置零，剔除其中的海杂波分量，得到新的Hankel矩阵。依据原始数据矩阵的构造方式，还原出信号的时间序列。图3为提出的海杂波抑制方法流程。

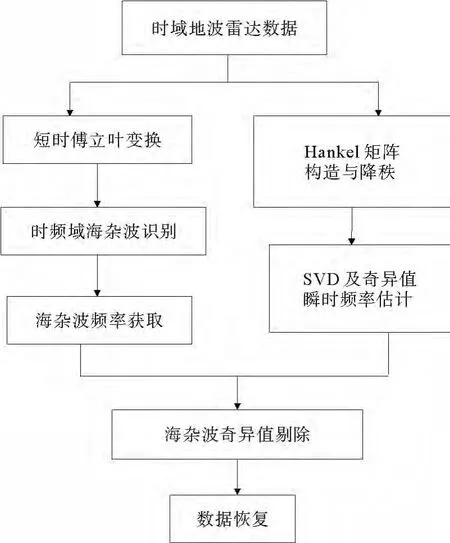
图3 海杂波抑制流程Fig.3 Flowchart of sea clutter suppression

通过时域序列数据构造矩阵时，也可先进行时频分析，只截取海杂波能量较强时段的雷达回波数据进行处理，以降低运算量。本方法将矩阵SVD和时频分析抑制算法有机结合，克服了前者杂波奇异值不易确定的问题，也避免了后者的逆变换与补偿重构问题。

3 实测数据分析与处理

为验证本文算法的有效性，利用在某高频地波雷达站采集的实测数据开展了海杂波抑制实验。实验系统的通道数据经插值处理后距离单元分辨率是1.5km，时域采样点间隔为0.14s。截取130s的雷达回波进行STFT变换，滑窗采用汉明窗，按距离单元分别对数据中所包含的信息进行分析处理。

图4（a）给出第21距离单元的STFT处理结果，图中以亮度越亮表示能量越强。由图4（a）可见，回波能量主要集中于4个频率变化区间内，即：1区间0.26～0.306 7Hz，2 区间 0.193 3～0.226 7Hz，3 区 间－0.093～－0.126 7Hz及4区间－0.28～－0.326 7 Hz。此时，雷达发射频率为8.9MHz，据布拉格频率公式计算一阶峰位置为fB＝±0.304 3Hz，正负一阶Bragg峰的频差为0.608 6Hz，频谱展宽约0.04Hz。另外，参照与之相间隔距离单元的情况，在频宽较小的频率范围2和3内无较强能量分布，满足船只目标在频谱中沿距离向的延展性不强的特征。由此可判定谱中频率范围1和4为一阶海杂波，范围2和3为船只目标。

图4（b）为矩阵SVD估计的4个奇异值所对应的瞬时频率，频率按相应的奇异值依次表示为w1，w2，w3及w4。其中，w1和w3在±0.3Hz附近小幅波动，在时频分析识别的一阶海杂波频谱范围之内，频率w1和w3对应的奇异值即为海杂波奇异值。

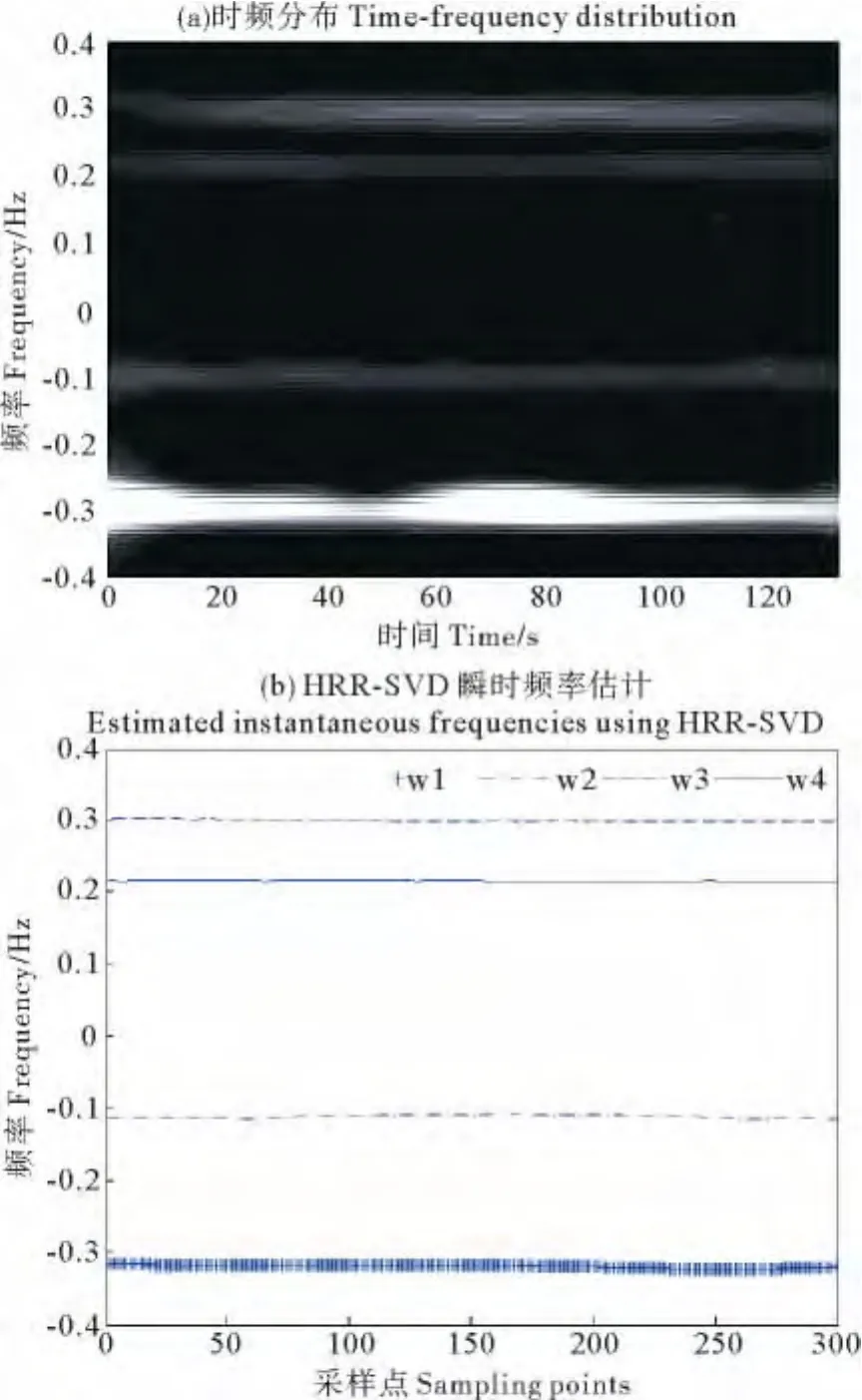
图4 回波信号时频分析Fig.4 Time-frequency analysis of received signals

图5给出海杂波抑制前后的时域波形及速度谱。图5（a）为只有海杂波存在时的时域信号，图5（b）为海杂波和2个船只目标同时存在的时域信号，图5（c）为船只目标所在距离单元的频谱。从图5（a）和图5（b）中可以看出，杂波抑制后海杂波主成分得到了显著的抑制。由图5（c）可见，相应距离单元中的目标信噪比提高了约20dB。此外，除海杂波区域外，目标的频谱特征没有受到任何影响。

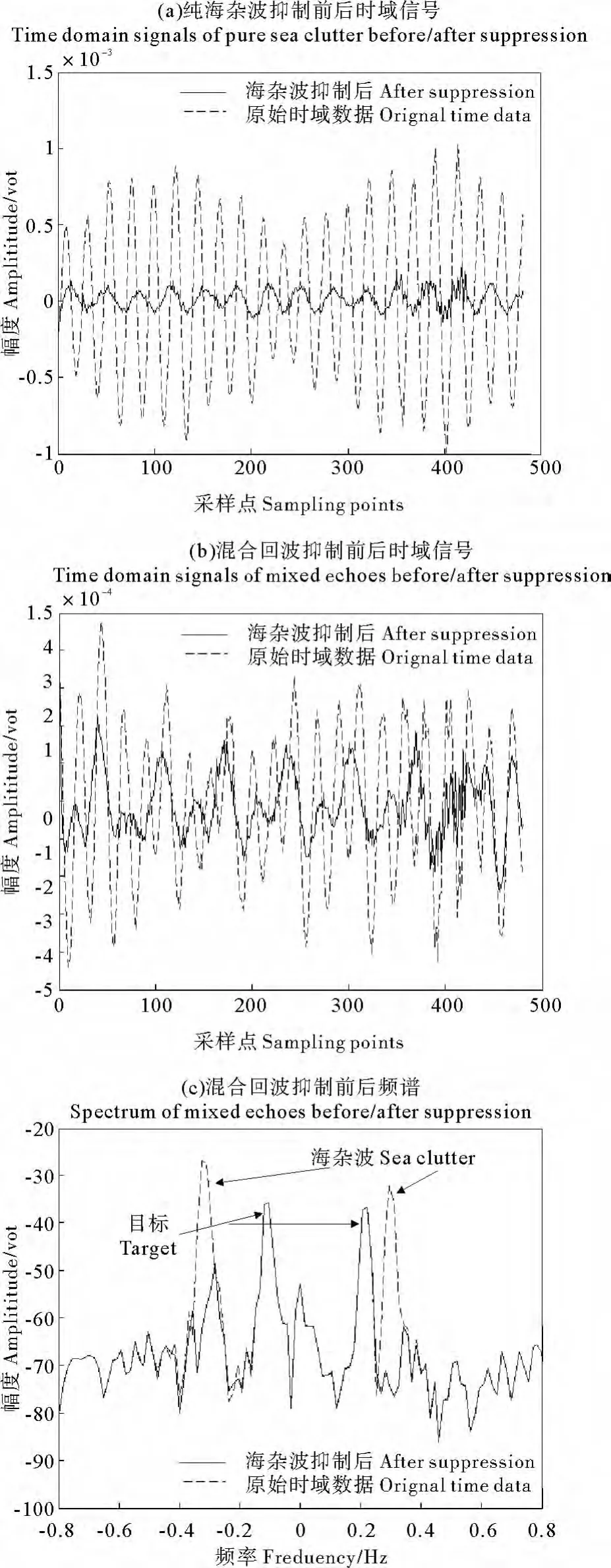
图5 海杂波抑制前后对比Fig.5 Results before/after suppression

为更加全面地衡量高频地波雷达作用距离内海杂波的抑制效果，将所有时域回波进行海杂波抑制，利用抑制前后的数据分别形成距离－多普勒（R-D）谱。采用CFAR检测算法［19］对此二维图像进行船只目标检测验证。首先，分别在距离向、频率向进行单元平均CFAR目标检测，综合虚警概率设为10－6。然后综合距离向、频率向检测结果，保留在距离域和频域均超过检测门限的目标。最后，经峰值检测输出检测结果。抑制前检测到的目标用圆圈标出，抑制后检测到的用小正方形标出（见图6）。

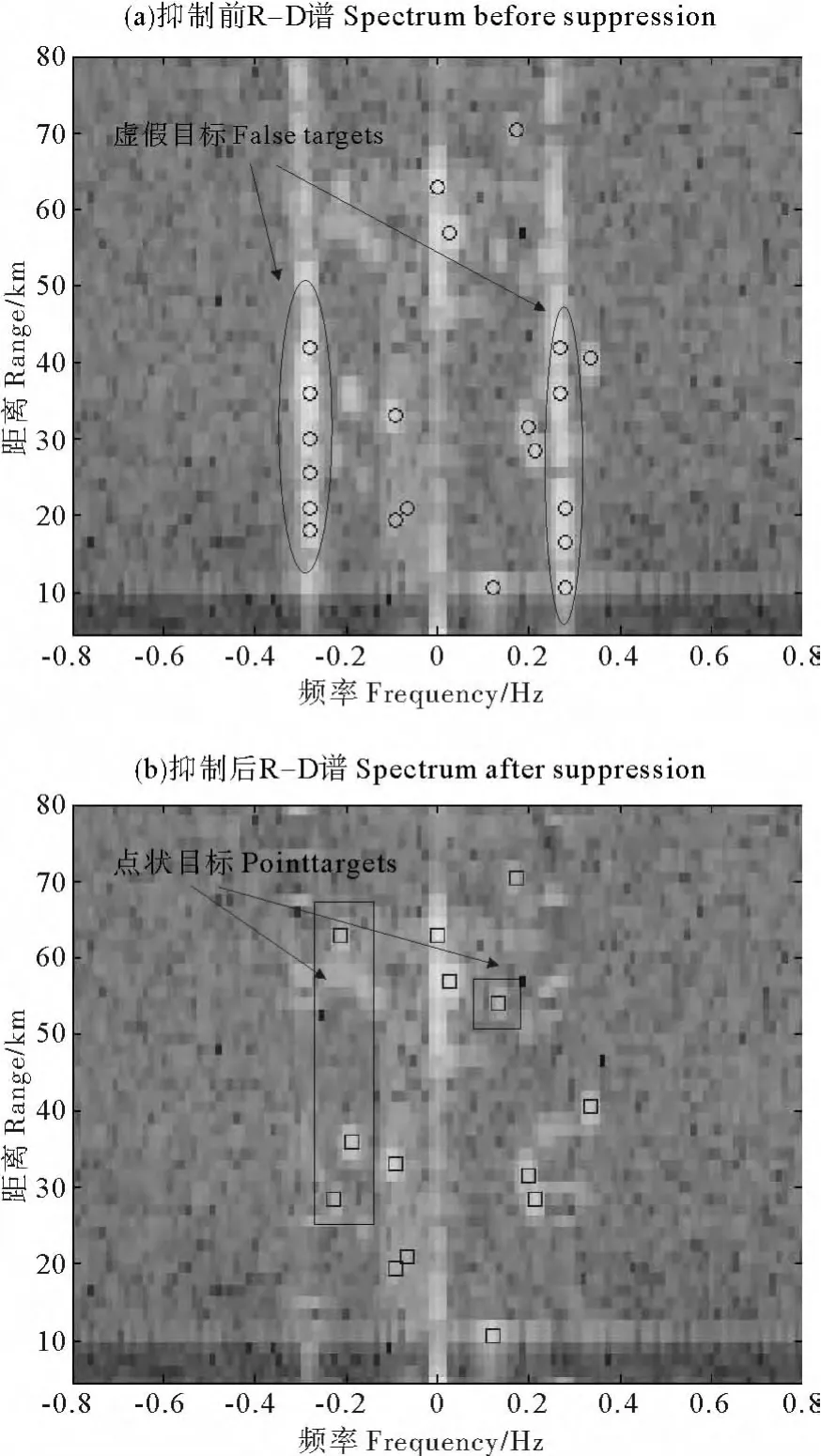
图6 抑制前后检测结果Fig.6 Detection results before/after suppression

由图6（a）可见，海杂波抑制前的R-D谱中2条海杂波峰的幅度非常高，强于附近的点状船只回波散射强度。经检测，海杂波区出现很多虚假目标（由椭圆框框出），而其周围的点状船只目标没有被检测到。从图6（b）给出的抑制后的R-D谱可以看出，海杂波抑制后的船只回波得到凸显，由海杂波引起的虚假目标被剔除，同时检测到之前漏检的点状船只目标（由矩形框框出），降低了海杂波对检测背景的影响，提高了船只目标的检测性能。

4 结语

本文分析了高频雷达海杂波的频率、幅度以及时频特性，提出了基于时频分析和矩阵分解联合的海杂波抑制方法。该方法综合利用多个处理域，丰富了海杂波抑制方法的信息量，提高了海杂波抑制效果。剔除海杂波后信杂比大大提高，而原始数据的其它时域及频域特征都得到了保留。经雷达实测数据验证，本文提出的方法有效提高了CFAR船只目标检测的能力，具有很好的应用前景。

［1］纪永刚，张杰，王祎鸣，等.双频地波雷达船只目标点迹关联与融合处理 ［J］.系统工程与电子技术，2014，36（2）：266-271.

［2］凡俊梅，焦培南，肖景明.海洋杂波对高频雷达检测海面上低速目标的影响 ［J］.电波科学学报，1997，12（2）：205-210.

［3］钱文振，纪永刚，王祎鸣，等.一种改进的地波雷达邻近距离单元格一阶海杂波对消方法 ［J］.海洋科学进展，2013，01：138-144.

［4］杨炼，孙合敏，潘新龙.基于扩展Prony算法的海杂波循环对消法［J］.现代雷达，2011，33（6）：53-57.

［5］Khan R.Ocean-Clutter model for high frequency radar［J］.IEEE Journal of Oceanic Engineering，1991，16（2）：181-188.

［6］WANG Jian.High Resolution Methods for Small Target Detection and Estimation in High Frequency Radar［D］.Canada：University of Victoria，2004.

［7］Poon W Y，Khan R，Le-ngoc S.A singular value decomposition based method for suppressing ocean clutter in high frequency radar［J］.IEEE Trans on Signal Processing，1993，41（3）：1421-1424.

［8］Khan R，Power D，Walsh J.Ocean clutter suppression for an HF ground wave radar［C］.IEEE conf on Electrical and Computer Engineering，1997，2：512-515.

［9］LI Yang，JI Zhenyuan，XIE Junhao，et al.Detection of HF firstorder sea clutter and its splitting peaks with image feature：results in strong current shear environment［C］.Advanced Concepts for Intelligent Vision Systems，Berlin：Springer，2012：503-514.

［10］周文瑜，焦培南.超视距雷达技术［M］.北京：电子工业出版社，2008.

［11］Barrick D E，Headrick J M，Bogle R W，et al.Sea backscatter at HF：interpretation and utilization of the echo［J］.Proc of the IEEE，1974，62（6）：673-680.

［12］Panagopoulos S，Soraghan J.Small target detection in sea clutter［J］.IEEE Trans on Geoscience and Remote Sensing，2004，42（7）：1355-1361.

［13］Haykin S，Bakker R，Curriew B.Uncovering nonlinear dynamics-The case study of sea clutter［J］.Proc IEEE，2002，90（5）：860-881.

［14］Lipa B J，Barrick D E.Extraction of sea state from HF radar sea echo：mathematical theory and modeling ［J］.Radio Science，1986，21（1）：81-100.

［15］董英凝，张宁，许荣庆.高频地波雷达工作环境对系统性能影响的分析 ［J］.电波科学学报，2007，22（2）：325-330.

［16］熊新农，万显荣，柯亨玉，等.基于时频分析的高频地波雷达电离层杂波抑制 ［J］.系统工程与电子技术，2008，30（8）：20-25.

［17］仇永斌，张宁，张树春.双基地高频地波雷达海杂波抑制［J］.哈尔滨工业大学学报，2012，44（1）：71-77.

［18］Dimonte C，Arun K.Tracking the frequencies of superimposed time-varying harmonics ［C］.Albuquerque：Proc ICASSP 90，1990，5：2536-2542.

［19］王腾，徐向东，范丛旺，等.两种检波方式CA-CFAR检测器性能分析 ［J］.空军雷达学院学报，2009，23（5）：356-358.