人工心脏泵流场的数值分析

刘汉涛，马理强，李海桥

（中北大学 机械与动力工程学院，山西 太原030051）

0 引 言

人工心脏泵采用体外灌注的方式保证衰竭心脏的血液循环，从而代替心脏的功能［1-2］.第一个人工心脏的研制距今已半个多世纪［3］，国内外的许多学者对心脏泵的形式也进行了不断改进，目前流线型叶轮叶片的离心式心脏泵在临床实验中由于具有更多的优点而被广泛采用［4-6］.然而流线型人工心脏泵内的机械磨损、溶血和血栓等现象仍很难消除［7-9］，这些都与血液的流体动力学行为相关，而流动中大尺度分离是造成升压比下降和血细胞破坏的主要原因［10-13］.为了解设计的心脏泵内流动细节，本文采用计算流体动力学（Computational Fluid Dynamics，CFD）方法［14-16］，对人工心脏泵内的流场和性能进行了模拟，得到心脏泵内部的详细流场，通过CFD数值计算结果，找出影响人工心脏泵性能的流动因素，分析心脏泵流场，特别是心脏泵内流动分离现象，对造成人工心脏泵内部流动分离、流动紊乱的因素进行分析，避免或改进设计过程中出现的分离现象.为设计更符合血液动力学要求的人工心脏泵，对人工心脏泵改进提出相应措施.

1 数学模型及数值方法

文中计算采用的质量守恒方程与Navier-Stokes方程形式为

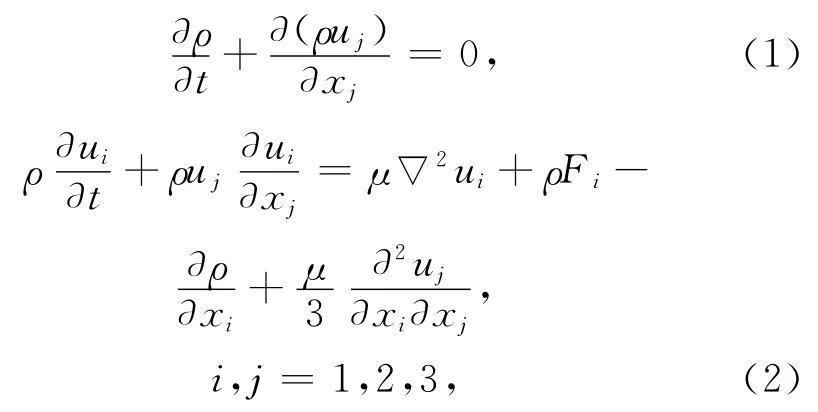
式中：ρ为流体密度；p为流体压强；u为流体速度；F为体积力；μ为粘性系数.

湍流模型采用k-ε双方程模型

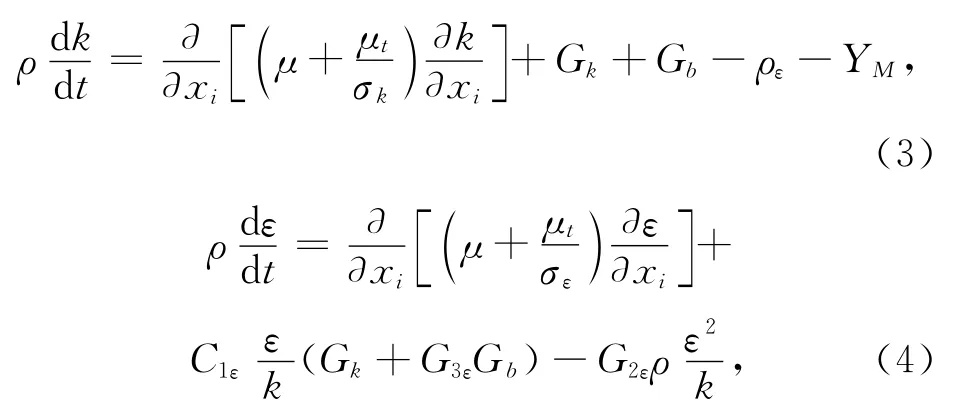
式中：Gk表示由于平均速度梯度引起的湍动能；Gb表示由于浮力影响引起的湍动能；YM表示可压缩湍流脉动膨胀对总的耗散率的影响；湍流粘性系数在计算过程中，取C1ε=1.44，C2ε=1.92，C3ε=0.09，湍动能k与耗散率ε的湍流普朗特数分别为σk=1.0，σε=1.3.

在壁面采用标准壁面函数法，衔接粘性底层低雷诺数区与湍流充分发展区，即在求解近壁区的k，ε时，将k-ε方程中的对流项及扩散项略去，得到k，ε的近似表达式

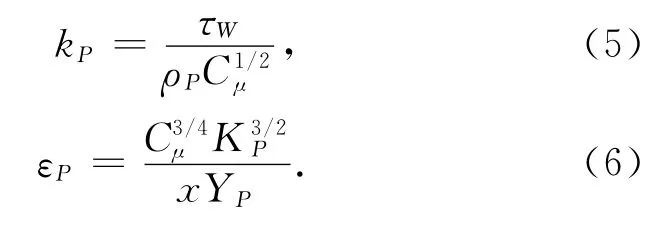
采用SIMPLE算法进行压强-速度耦合.计算区域采用非结构化网格，经过网格无关解的测试，最终计算采用节点数262 586.计算过程中采用的时间步长10-4s.

2 边界条件

设置计算边界条件如表1所示.叶轮转速10 000 r／min.在计算的流速范围内设置血液是不可压缩的流体，密度为1.055×103kg／m3，粘度为4×10-3Pa·s.进出口压差为13 332.2 Pa.其它壁面定义为无滑移固壁边界条件.

表1 计算边界条件 Tab.1 Boundary conditions of computation

3 计算结果分析

对泵内速度及压力分布进行了求解，图1为泵内压力云图，泵进出口压力差13 332.2 Pa，但整个泵最高压力为18 000 Pa，出现在动叶片出口处，由于局部阻力与沿程损失，在静止导叶片出口处，表压降到13 500 Pa左右，泵内最低的压力出现在动叶片进口位置.

图1 心脏泵内压力云图 Fig.1 Pressure cloud picture of the artificial heat pump

图2为泵轴的中间截面流速分布情况.计算结果显示，泵内速度在0.2～6.9 m／s之间.

图2 泵中间截面速度分布 Fig.2 Velocity distribution of the pump center section

从这些区域可以看到，流动未受到叶片的干扰，没有明显的流动分离、涡流、滞流等现象出现.其中0.2～3 m／s的速度分布区域，6～6.9 m／s的速度分布区域分别如图3和图4所示.

图3 0.2～3 m／s速度分布区域 Fig.3 Velocity domain of 0.2～3 m／s

图4 6.0～6.9 m／s速度分布区域 Fig.4 Velocity domain of 6.0～6.9 m／s

在动叶片区，由于叶片的高速旋转运动，泵内最高流速达到6.9 m／s，泵内动叶片区速度在3～6.9 m／s，流速较高的区域主要集中在动叶片出口位置之前的一片区域.从图5可以看出，最高流速在轮缘处.在计算过程中，对动叶片外缘与外部套筒之间的间隙做了简化处理，但通过分析可以得出，在固定的外部套筒壁面附近，由于流体的粘性和受壁面摩擦阻力的影响，紧贴壁面处会形成速度梯度很大的边界层，这一微小的间隙内必定产生较大的剪切应力.很容易产生溶血和血栓，对血液造成破坏.因此，应正确确定间隙，既能减少轴向泄漏，又要保证适当的剪切应力.进口导流区域及出口导叶区域流速较低，流动速度在0.2～3 m／s之间.

图6为动叶片轮缘周向0～180°范围内的速度矢量，可以看出在血液由导流体区流入动叶片区时，由于流动速度和流动方向的忽然改变，流动出现了重复循环、流动分离、涡流等不规则的流动模式.流体流出动叶片区进入导流区时也出现了微小的流动分离.为改善流体进入动叶片区产生的流动分离，应改变导流体形状，使流出导流体的流动方向与动叶片入口处切线方向一致.在其它区域流动速度分布比较均匀平缓，符合生理要求.

图5 动叶片径向速度分布 Fig.5 Radial velocity distribution of moving blade

图6 动叶片区轮缘周向0～180°区流速分布Fig.6 Velocity distribution of 0～180°wheel rim

图7为动叶片压力面与吸力面速度分布，可以看出流体流动方向与流线形外形基本一致，也存在微小的流动方向发生改变的情况，表明叶片形状仍存在改进的余地.

图8为静止导叶片区速度分布，可以看出，在流经静止导叶片区时，流动方向与静止叶片方向逐渐一致，在出口位置流动达到比较理想的情况.

图9中左侧位置是流体入口，右侧为流动出口，从入口不同位置分别标识了7条流体的流动迹线，可以看出，除了进入和流出动叶片位置处流动方向发了较明显的改变外，在其它区域流动方向与叶片形状比较吻合.这也表明，导流体的外形需要做出改进.

图7 叶片压力面与吸力面速度分布 Fig.7 Velocity distribution of pressure surface and the suction surface

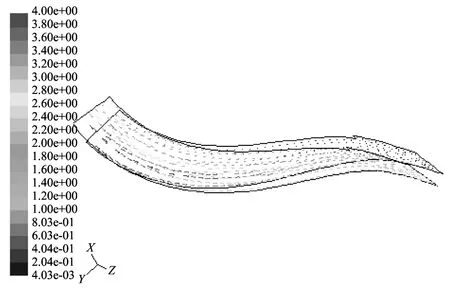
图8 静止导叶片速度分布 Fig.8 Velocity distribution of stationary guide blade

图9 自入口到出口按速度标识的迹线 Fig.9 Velocity trace from the entrance to the exit

4 结 论

1）从泵总体流场看，在导流区、动叶叶片区、导叶区流动比较平缓，流动迹线与流线型外形比较一致，没有明显的流动分离、涡流、滞流等现象出现；

2）在动叶片外缘速度较高，动叶片外缘与外部套筒之间存在边界层区，这一区域有较大的速度梯度，产生较大的剪切应力，是产生溶血、血栓和血液破坏的重要原因；

3）在动叶片入口及出口位置存在流动的突然改变，特别是动叶片入口区，由于导流体外形及流向与动叶片入口设计问题，导致这一区域产生了重复循环、流动分离、涡流等不规则的流动模式；

4）动叶片压力面、吸力面及静止导叶片部分的流动方向与流线型叶片外型基本一致，也存在微小的流动方向发生改变的情况，表明叶片外形的进一步优化可更加改善流场情况，更符合血液的流体动力学行为；

5）带动叶片与外部套筒间隙、改进进口导流体模型等不同流动模型的计算结果仍需进一步研究.

［1］Tzallas A T，Katertsidis N S，Karvounis E C，et al.Modeling and simulation of speed selection on left ventricular assist devices［J］.Computers in Biology and Medicine，2014，51：128-139.

［2］Babamir S M，Dehkordi M B.Specification and simulation of behavior of the continuous infusion insulin pump system［J］.Bio-Medical Materials and Engineering，2014，24（2）：1517-1526

［3］Marsden A L，Bazilevs，Y，Long C C，et al.Recent advances in computational methodology for simulation of mechanical circulatory assist devices［J］.Wiley Interdisciplinary Reviews-Systems Biology and Medicine，2014，6（2）：169-188.

［4］阮晓东，陈松松，钱伟文，等.基于溶血性能的离心式旋转血泵设计［J］.中国生物医学工程学报，2011，30（3）：411-415.Ruan Xiaodong，Chen Songsong，Qian wenwei，et al.Design of centrifugal blood pump based on hemolysis estimation［J］.Chinese Journal of Biomedical Engineering，2011，30（3）：411-415.（in Chinese）

［5］Bakouri M A，Salamonsen R F，Savkin A V，et al.A sliding mode-based starling-like controller for implantable rotary blood pumps［J］.Artificial Organs，2014，38（7）：587-593.

［6］Niklas A，Hiller K A，Jaeger A，et al.In vitro optical detection of simulated blood pulse in a human tooth pulp model［J］.Clinical oral investigations，2014，18（5）：1401-1409.

［7］Cruz D O A，Pinhof T.Turbulent pipe flow prediction with a low Reynolds number type closure［J］.Journal of Non-Newtoinan Fluid Mechanics，2003，114（2／3）：149-184.

［8］刘云，李世嘉，侯击波，等.精密铝铸件电磁泵负压充型测试技术［J］.测试技术学报，2009，23（3）：213-216.Liu Yun，Li Shijia，Hou jibo，et al.Testing technique of negative pressure mold-filling of electromagnetic pump for precision aluminum casting［J］.Journal of Test and Measurement Technology，2009，23（3）：213-216.（in Chinese）

［9］Peng Y H，Wu Y Q，Tang X Y，et al.Numerical simulation and comparative analysis of flow field in axial blood pumps［J］.Computer Methods in Biomechanics and Biomedical Engineering，2014，17（7）：723-727.

［10］Wu Huachun，Wang Ziyan，LüXujun.Desigh and fluent simulation of impeller for axial maglev heart pump［J］.Applied Mechanics and Materials，2012，195：29-34.

［11］苏波，王登伟.一种新型无阀微泵的研究［J］.测试技术学报，2011，25（2）：107-111.Su Bo，Wang Dengwei.Research of a novel valveless micropump［J］.Journal of Test and Measurement Technology，2011，25（2）：107-111.（in Chinese）

［12］Abdoli A，Dulikravich G S，Bajaj C，et al.Human heart conjugate cooling simulation：unsteady thermofluid-stress analysis［J］.International Journal for Numerical Methods in Biomedical Engineering，2014，30（11）：1372-1386.

［13］Long C C，Esmaily-Moghadam M，Marsden A L，et al.Computation of residence time in the simulation of pulsatile ventricular assist devices［J］.Computational Mechanics，2014，54（4）：911-919.

［14］Song G L，Chua L P，Lim T M.Numerical study of of bio-centrifugal blood pump with straight impeller blade profiles［J］.Artificial Organs，2009，34（3）：98-104.

［15］Lim E，Salamonsen R F，Mansouri M，et al.Hemodynamic response to exercise and head-up tilt of patients implanted with a rotary blood pump：a computational modeling study［J］.Artificial Organs，2015，39（2）：24-35.

［16］Kafagy D H，Dwyer T W，Mc Kenna K L，et al.Design of axial blood pumps for patients with dysfunctional fontan physiology：computational studies and performance testing［J］.Artificial Organs，2015，39（1）：34-42.