基于MRAS的无速度传感器矢量控制系统研究
刘冬冬,陈文燕,周 申,符冬冬
(西安科技大学 电气与控制工程学院,陕西 西安710054)
异步电机矢量控制(Vector Control,VC)具有控制精度高、低频特性好,转矩响应快等动静态控制性能,从而广泛应用于交流电机高性能传动领域.但是,传统矢量控制的转速反馈信号是通过安装速度传感器获得转速信息的.而无速度传感器矢量控制技术是从电机端获得电压电流等物理量,通过计算估算出电机转速,它省去了速度传感器带来的硬件检测的麻烦,降低了系统的成本,提高了系统的稳定性.基于模型参考自适应(Model Reference Adaptive System,MRAS)的转速识别方法具有算法简单、计算量小、实时性和稳定性好等优点,在许多领域得到了广泛的应用.因此,本文基于MRAS算法设计一套电动机交流变频调速系统.
1 矢量控制
1.1 基本原理

异步电机矢量控制原理就是根据电机的动态数学模型,利用PARK变换和CLARK变换,将异步电机模拟成直流电机,从而获得更好的控制性能.在产生同样旋转磁动势的前提下,在ABC三相坐标系下的定子电流iA,iB,iC通过CLARK变换(即3s/2s变换),可以转换为αβ两相静止坐标系下的电流iα,iβ,再经过PARK变换(即2s/2r变换),将αβ两相静态坐标系转换为dq两相旋转坐标系,把电机的定子电流分解为相互垂直的励磁电流id和转矩电流iq,这样观察者站在铁心上与坐标系一起旋转,交流电机就可以等效为直流电机,因此就可以应用控制直流电机的方法来控制交流异步电机了.其原理图如图1所示,iA,iB,iC为三相交流输入电流,ωr为输出转速.

图1 矢量控制原理图 Fig.1 Vector control schematics
1.2 转子磁链的电流模型
从异步电机的数学模型中可以看出,电机是一种多变量、非线性、强耦合的系统,如控制直流电机那样控制交流电机,必须进行矢量变换.
通过矢量变换,可以得到在dq坐标系下的电机的电压方程式为

式中:Usα,Usβ为两相静止坐标系中的定子绕阻电压;Urα,Urβ为两相静止坐标系中的转子绕阻电压;isα,isβ是两相静止坐标系中定子绕阻电流;irα,irβ是两相静止坐标中的转子绕阻电流;ωr是转子角速度;Rs,Rr是定转子绕阻电阻;Ls,Lr是定转子绕阻自感;Lm是两相坐标系下的同轴定转子绕组之间的互感;ρ为微分算子.
在两相静止坐标系下的转子磁链在αβ轴的分量为

所以,对应的电流方程为


经过相关换算推导可得出异步电机转子磁链电流模型的方程为

因此,转子磁链在旋转两相坐标系下的电流模型方程为

电动机转差公式为
式中:Tr为转子电磁时间常数,Tr=Lm/Rr.
1.3 转子磁链的电压模型
根据异步电机在αβ两相静止坐标系中的变换可以得到转子磁链的电压方程.

式中:ψrα,ψrβ分别是转子磁链在αβ轴的分量;usα,usβ分别是定子电压在αβ轴的分量;isα,isβ分别为定子电流在αβ轴的分量.
2 基于转子磁链的MRAS转速辨识
MRAS的基本原理是:对一个可建立数学模型并且参数或者变量不完全可测量的系统,利用一个参考模型和一个可调模型的输入误差,来设计一个可以改变系统中某一个或者某些参数的自适应结构,通过参数或者变量调节动作来改变可调模型的输出值,使得参考模型和可调模型的输出误差为零[3],参考模型自适应系统如图2所示.
由转子磁链的电压模型公式(10)和(11)可知,该公式中不含未知变量转速,因此把该项作为参考模型,即理想输出量,由转子磁链的电流模型公式(6)和(7)可知该项中含有所需变量转速,因此把该项作为可调变量,即实际输出变量.根据Popov 稳定性理论可得公式
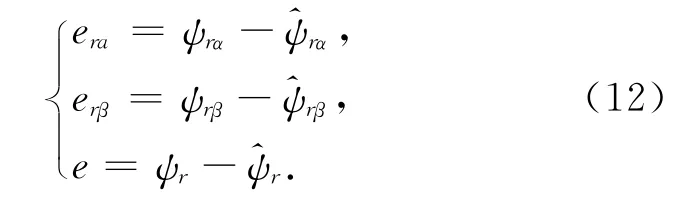
即
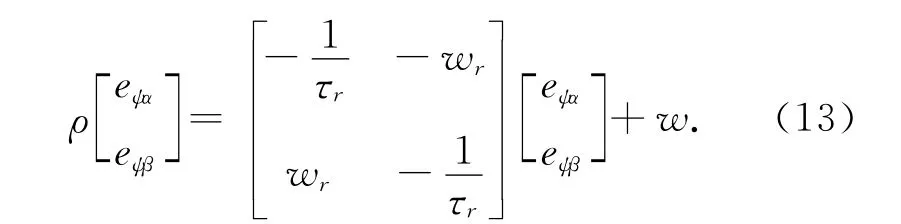

图2 参考模型自适应系统结构框图 Fig.2 Adaptive system structure of reference model
根据Popov稳定性理论可知反馈部分的必须满足Popov不等式,反馈部分的方程为

由于反馈一般都含有比例和积分,因此设估计出的转速为

若满足超稳定定理则在t>0时,有

因此可得到

由此根据Popov超稳定定理可推导出电动机转速公式
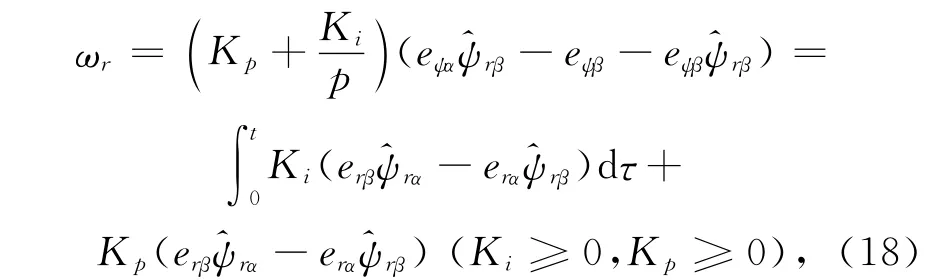
式中:Kp,Ki为PI调节器的参数.
3 硬件构成
异步电动机无速度传感器矢量控制系统包括主电路和控制电路两部分,首先从电网引出的三相对称交流电源经过整流桥得到直流电,再经过滤波电路后送入智能功率模块(IPM)组成的逆变电路.通过PWM信号来触发IGBT的通断,从而来控制电动机的运行.主电路由整流电路、启动电路、滤波电路、逆变电路等组成.控制电路主要是以TMS320F28335DSP为核心,由光耦电路、故障检测电路、电压调理电路等组成,通过DSP的ADC对电动机的电压电流进行采样,从而达到对电动机转速的实时监控.其硬件框图如图3所示.

图3 异步电动机调速系统硬件结构框图 Fig.3 Hardware structure diagram of asynchronous motor speed control system
4 系统软件设计
该系统的程序主要有主程序和中断服务程序两部分组成.主程序用来完成系统初始化及调节器的初始化.中断服务程序主要完成对电动机的转速调节.流程如图4和图5所示.

图4 主程序流程图 Fig.4 Main program flow chart

图5 中断服务程序流程图 Fig.5 Interrupt service program
5 实 验
利用实验的方法来验证无速度传感器矢量控制系统的正确性.所用的交流电机主要参数为:u=260 V,f=50 Hz,np=2,Rs=0.435Ω,Lls=0.002 m H,Rr=0.816Ω,Llr=0.002 m H,Lm=0.069 m H,J=0.19 kg·m2.定转子绕组自感为0.071 m H,漏磁系数为0.056,转子时间常数是0.087.电机空载启动,给定的转速为1 200 r/min,当t=0.6 s时,电机加负载转矩TL=55 N·m.
图6和图7为电动机实际转速和估计转速波形.结合图6和图7可知,在电动机启动的初始阶段0~0.22 s时,电动机转速慢慢变大,与实际状况相符,转速误差较小,在0.22~0.6 s阶段,电动机转速始终是在所设定的转速1 200 r/min左右,虽然估算转速有波动,但是起伏较小,系统较稳定,在0.6 s时,系统外加入负载,估计转速有波动,但很快就恢复到所设定的转速1 200 r/min.由整个仿真时间内的波形可知:该系统对电动机转速估计误差很小,波动也很小,系统始终处于一个比较稳定的状态.

图6 实际转速Fig.6 Actual speed

图7 估算转速 Fig.7 Estimated speed
6 结 论
本文提出的无速度传感器矢量控制系统实质上是通过采集电动机电流电压值,然后经过MRAS算法估算出电动机转速,从而替代了传感器的作用,减少了系统的成本,扩大了系统的使用范围.仿真结果表明,该系统可以有效地对电动机转速进行估算,使系统可以获得更好的动态特性,在加入负载后电动机可以平稳达到所要求的转速.这种方法实现非常简便,特别是省略了速度传感器,提高了电动机调速的自动化水平,对实际工程有一定的指导意义.
[1]李华德,白晶,李志民,等.交流调速控制系统[M].北京:电子工业出版社,2002.
[2]夏朝英.交直流传动系统的自适应控制[M].北京:机械工业出版社,2005.
[3]Li Zhen.Sensorless field orientation control of induction machines based on a mutual MRAS scheme[J].IEEE Trans on IE,1998,45(5).
[4]Elbuluk M E,Kankam D.Speed sensorless induction motor driver for electrial actuators:schemes,trends and tradeoffs[C].Aerospace and Electronics Conference,1997.NAECON 1997,Proceeding of the IEEE1997 Nation,1997(1):137-144.
[5]洪乃刚.电力电子、电机控制系统建模和仿真[M].北京:机械工业出版社,2010.
[6]Cirrincione M,Pucci M.An MRAS based on speed estimation method with a liner neuron for high performance inductor motor drives and its experimentation[C].Proceedings of the IEEE IEMDC,2003:617-623.
[7]Marko Hinkkanen.Analysis and design of full-order flux observers for sensorless induction motor[J].IEEE Trans.Ind,Electron,2004,51(5):1033-1040.
[8]Kalman P E.A new approach to linear filtering and prediction problems[J].Transaction of the ASMEJournal of Basic Engineering,1960:35-45.
[9]Holtz J.Sensorless control of induction motor driver[J].Proc.of IEEE,2002,90(8):1359-1394.
[10]Rao S,Buss M,Utkin V.Sliding mode based stator flux and speed observer for induction machine[C].IEEE,International Workshop on Variable Structure Systems,2008:95-99.

