球扁药药型尺寸对内弹道性能的影响

刘 佳，马忠亮，程 山，萧忠良

（1.中北大学 化工与环境学院，山西 太原030051；2.江河化工科技有限公司，湖北 宜昌444200）

0 引 言

球扁发射药因其装填密度高、流散性好、渐增性燃烧特性好［1-2］，大幅度提高武器初速，提升了武器综合性能，加之制造工艺简单、经济效益显著等优点，逐渐为各国重视，并已经广泛用于中小口径速射武器、榴弹发射器等武器系统装药［3-4］.国内研制并装备部队的轻武器系统，大部分采用球扁发射装药.随着大弧厚球扁发射药的研制［5-6］，其有望应用于大口径武器系统，进一步拓展了其应用范围［7-8］.但球扁发射药尺寸小，较小的尺寸误差易对内弹道性能（最大膛压及初速）产生较大影响［9］.本文以5.8 mm枪为平台从理论上计算出不同药型尺寸球扁发射药混装时对应的最大膛压及初速，并通过实验获得球扁发射药过筛前后的初速，由此分析球扁发射药药型尺寸变化对武器系统内弹道性能的影响.

1 理论计算

1.1 球扁发射药形状函数推导

为方便计算，对球扁发射药药型进行简化处理［10-11］，药粒可看作底面为椭圆的柱体，柱体高看作药粒弧厚，椭圆短径为2a，长径为2b，高为2e1，而且2e1＜2a＜2b；起始体积为V1.按照同时着火假设和平行层燃烧规律，当燃去厚度e时，药粒的全部表面都向内燃烧推进了e.假设所有的药粒都具有相同的外形尺寸，用一个药粒推导出的Ψ代表全部装药的相对已燃部分，药的几何模型见图1.

图1 球扁药的几何模型 Fig.1 Geometry model of oblate spherical propellants

对球扁发射药药粒有

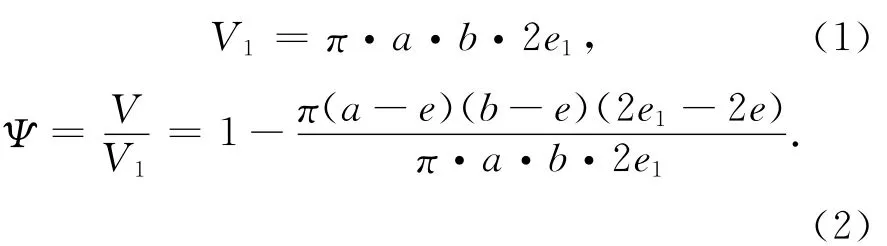
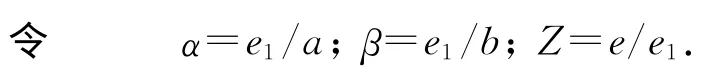
将式（2）展开，并把α，β，Z代入其中，整理得

其中

1.2 经典内弹道模型

本文中所用的内弹道方程是基于以下的基本假设［12］：①火药燃烧遵循几何燃烧定律；②药粒在平均压力下燃烧，且遵循燃烧速度定律；③用系数φ来考虑其他的次要功；④弹丸挤进膛线是瞬时完成，以一定的挤进压力p0标志弹丸的启动条件；⑤火药燃气服从诺贝尔-阿贝尔状态方程；⑥弹丸挤进膛线后，密闭良好，不存在漏气现象；⑦混合燃气质量、能量等于各单一火药燃气相应质量、能量之和；⑧只求混合燃气的平均压力，不考虑单一燃气分压问题.

根据内弹道基本假设，将内弹道方程组归纳如下：

设有i种弧厚的球扁发射药，含量为xi，对应的弧厚、已燃百分数和已燃厚度分别为ei，Ψi和Zi，对应形状特征量为χi、λi、μi，则有

1）形状函数

2）燃速方程

3）弹丸运动方程

4）弹丸速度与行程关系式

5）内弹道基本方程

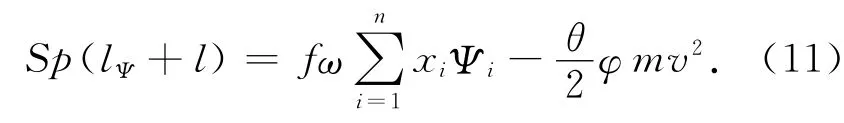
这些方程联立起来，组成了混装球扁发射药内弹道基本方程组，其中

式中：χ，λ，μ分别为形状特征量；z为相对厚度；u为火药燃速，m·s-1；u1为火药燃速系数，m·MPa-n·s-1；n为燃速指数；S炮膛横断面积，m2；m为弹丸质量，kg；p为压力，Pa；φ为次要功系数；v为弹丸运动速度，m·s-1；l为弹丸行程，m；lψ为药室自由容积缩径长，m；f为发射药火药力.

1.3 计算条件

由于生产工艺条件的限制，所生产的球扁发射药形状尺寸不可能完全一致，会含部分其他尺寸的球扁药粒，对最大膛压和初速均会产生影响.本文以可能出现的几种理想情况为例，采用C语言编程，联立内弹道方程组，结合四阶龙格库塔方法，以5.8 mm枪为平台计算出内弹道参数最大膛压及初速.

假设制得的球扁发射药弧厚含有0.13，0.14，0.15和0.16 mm四种情况，按弧厚的增加依次记作e1，e2，e3和e4.

同时假设在装药过程中球扁发射药以下几种弧厚尺寸理想混装，如表1所示.

表1 发射药各尺寸含量变化 Tab.1 Content change of propellants'grain size

1.4 计算结果及讨论

通过理论模拟计算出不同弧厚球扁药混装下的最大膛压及初速，如表2所示.

表2 理论计算结果 Tab.2 Results of theoretical calculation

本文模拟计算几种理想混合装药情况，由于工艺条件差异或是偶然因素制得球扁发射药尺寸必然存在一定误差.因此，在实际装药过程中，不同弧厚球扁药混装更为复杂.由数值计算结果可以看出，即便几种不同弧厚球扁发射药理想混装得到初速与最大膛压不尽相同，随着弧厚尺寸增加，所得初速与最大膛压均有所下降.这是由于弧厚越大，燃烧所用时间越长，能量释放相对缓慢，最大压力点出现滞后现象.由第2和第5组数据可以看出，即便单一尺寸的球扁药中混入少许其他尺寸亦可对最大膛压及初速产生较大影响；由第3，5，6，7组数据可以看出，当混装的球扁发射药弧厚数越多时，最大膛压及初速变化量越大；后3组数据较前4组数据最大膛压及初速跳动变化较小，即若不能保证发射药弧厚完全一致时可适当将不同弧厚发射药混装以减小初速及最大膛压的跳动.在实际装药中，大尺寸和小尺寸药粒对最大膛压及初速的影响相互制约，产生综合效果.

2 靶场实验

2.1 测试系统及方法

测速系统采用多普勒雷达测速系统，实验方法采用国家标准中的方法.

2.2 实验条件

以5.8 mm枪为实验平台进行两组靶场实验.第一组测试条件为：对制式弹药随机抽选20发，进行初速测试.第二组测试条件为：将双基球扁发射药用32～36目斜面振动筛进行处理，随机取100粒进行尺寸测量，其弧厚标准方差由0.023降至0.014，弧厚极差由0.1 mm降至0.07 mm，长直径标准方差由1.606降至0.830，短直径标准方差由0.492降至0.301，发射药形状尺寸更为均匀，其他参量仍为随机选取，选20发进行初速测试.

2.3 实验结果及分析

所得靶场实验结果见表3，以初速为例进行分析.

由靶场所得实验数据，计算出球扁发射药筛分前后初速极差（Δ）、平均偏差（μ）和或然误差（γ）［13-14］分别为：γ1=4.324，Δ1=28，μ1=5.05，γ2=2.817，Δ2=15，μ2=3.60.

可以看出，球扁发射药尺寸更均匀后，获得初速极差、平均偏差和或然误差均有所下降，即初速一致性变好，最大膛压亦是如此.球扁发射药较小弧厚误差不仅给武器系统带来安全隐患，亦会影响其射击精度，提高球扁药尺寸均一性是球扁发射药工艺亟需解决的难题.

表3 靶场实验结果 Tab.3 Results of range experiments

因此，提高弹道一致性的措施可从两方面入手：①改善球扁发射药的生产工艺和控制技术，提高产品初始弧厚的一致性，这对生产工艺和设备提高提出了较高要求；②在现有工艺和质量控制技术条件下，提高良品率的同时进行合理筛选分级，可将弧厚等级较薄和较厚的发射药进行混装，还可以针对弧厚较薄的发射药，通过减小装药量、提高膛压的方法达到p-l弹道曲线下面积基本不变的目的，从而保证弹道一致性，针对弧厚等级较厚的发射药，可通过增加装药量、减小膛压的方法达到相同的弹道效果.

3 结 论

1）5.8 mm枪的初速及最大膛压均随着球扁发射药弧厚的增加有所降低.当单一尺寸球扁发射药中混装少量其他尺寸给最大膛压及初速带来较大影响，并且混装尺寸量越多，最大膛压及初速变化量越大.几种混装方式较单一尺寸装药，最大膛压及初速跳动减小.

2）球扁发射药尺寸不均一性造成最大膛压及初速的跳差必然将会对武器系统寿命及射击精度带来不利影响，应改进球扁药生产工艺或装药方式，提高弹道一致性.

［1］孟凡军.球形药成型和表面钝感“一步法”工艺研究［D］.南京：南京理工大学，2010.

［2］潘仁明.径向变密度球扁药制备工艺和燃烧性能研究［D］.南京：南京理工大学，2009.

［3］殷继刚.多气孔球扁发射药结构、成型工艺及性能［D］.南京：南京理工大学，2006.

［4］陆安舫，云小侃，陈兴泉.球形药新进展［J］.火炸药学报，1998（2）：39-42.Lu Anfang，Yun Xiaokan，Chen Xingquan.Recent progress in spherical power［J］.Chinese Journal of Explosives ffPropellants，1998（2）：39-42.（in Chinese）

［5］袁伟忠.大弧厚双基球扁药的制造［D］.南京：南京理工大学，2003.

［6］王倡春.大弧厚球扁药的钝感性能研究［D］.南京：南京理工大学，2004.

［7］肖正刚，周伟良，应三九，等.球扁药应用于大口径火炮高装填密度发射装药［J］.火炸药学报，1999（4）：63-66.Xiao Zhenggang，Zhou Weiliang，Ying Sanjiu，et al.The application of oblate spherical powder to high loading density gun propellant charge［J］.Chinese Journal of Explosives ffPropellants，1999（4）：63-66.（in Chinese）

［8］肖正刚，施杰，应三九，等.大弧厚深钝感球扁药的定容燃烧性能［J］.弹道学报，2000，12（2）：6-9.Xiao Zhenggang，Shi Jie，Ying Sanjiu，et al.The isovolumetkic burning performance of deep-deterred oblate spherical power with large web［J］.Journal of Ballistics，2000，12（2）：6-9.（in Chinese）

［9］肖忠良.高精度速射武器装药研究［R］.内部报告，2012.

［10］白沐炎.新型35 mm枪榴弹发射器仿真建模与优化［D］.南京：南京理工大学，2006.

［11］李化耀.某遥控特种机械的动力学建模仿真与分析［D］.南京：南京理工大学，2008.

［12］金志明.枪炮内弹道学［M］.北京：北京理工大学出版社，2004.

［13］徐晓岭，王蓉华.概率论与数理统计［M］.上海：上海交通大学出版社，2013.

［14］于培彦.应用概率统计［M］.北京：清华大学出版社，2013.