PEMFC极化曲线半经验模型的改进

李 平，童晓敏，郝 冬，侯永平

(1.同济大学新能源汽车工程中心，上海 201804； 2.上海机动车检测中心，上海 201805)



·科研论文·

PEMFC极化曲线半经验模型的改进

李 平1，童晓敏2，郝 冬1，侯永平1

(1.同济大学新能源汽车工程中心，上海 201804； 2.上海机动车检测中心，上海 201805)

根据实验测得的数据，对燃料电池的极化曲线进行特性分析，归纳建模方法，在Kim模型和Fraser模型的基础上，针对小电流密度区间拟合精度低和拟合参数过多的问题，修正了活化损耗项，提出了改进的半经验模型。比较3个模型拟合结果的鲁棒性和精确性，建立的半经验模型拟合精度更高，实用性更强。

燃料电池； 极化曲线； 半经验模型

极化曲线特性研究可帮助分析燃料电池发动机的性能，半经验模型可根据方程中参数所代表的物理意义来描述工作过程，有助于了解和优化燃料电池的性能。关于燃料电池极化曲线的经验或半经验模型都有各自的优缺点。J.Kim等[1]提出只需测得电流、电压，就可较精确地拟合极化曲线的经验模型(Kim模型)，但在小电流密度区间拟合效果差且不能得到开路电压。D.Chu等[2]在此基础上提出的半经验模型，仅在大电流密度区间计算产生的浓差损失；S.D.Fraser等[3]引入损失电流密度和交换电流密度，并修正模型中的活化损失项，得到Fraser模型，但需要测得温度、压强等数据；H.Weydahl等[4]考虑将3种损失项都作为内部电流的影响；C.K.Poh等[5]提出可在整个电流工作区间都拟合浓差损失的经验模型。这些模型都有对浓差损失项描述太复杂、拟合参数多的问题。

本文作者对一些典型的模型进行总结，以Kim模型和Fraser模型为基础，建立了一个可在全电流密度区间拟合的极化曲线半经验模型，试图准确地预测燃料电池的性能。

1 半经验模型的比较

公式的部分参数，将所引用文献的编号数字加入下标中，公式中上标加撇号代表拟合参数，以作区别。

1.1 Kim模型

J.Kim等[1]提出的燃料电池极化曲线的经验模型为：

(1)

(2)

式(1)、(2)中：Erev为可逆电压；b为Tafel斜率；j0为交换电流密度；R为欧姆阻抗；m和n为无物理意义的拟合参数(m和n均大于0)。EO并非真正的开路电压，而仅是一个拟合参数，近似地代表开路电压；blg(j)代表活化损失；Rj代表欧姆损失；mexp(nj)代表浓差损失。该模型可在温度、湿度、压强和气体浓度等工作条件未知的情况下，仅需要电流和电压数据，即较精确地拟合极化曲线。由于blg(j)项的存在，导致即使在实验中测得了开路电压，也不能代入模型中进行拟合。该模型在小电流密度区间内的拟合效果不理想，拟合的结果与实际极化曲线偏差较大。

1.2 Fraser模型

Fraser等提出的极化曲线经验模型为：

(3)

式(3)中：jloss为损失电流密度，包括内部短路电流密度和氢气渗透电流密度。当氢气和氧气的分压和电堆工作温度已知时，可以求得可逆电压。S.D.Fraser等[3]主要针对Kim模型不能拟合开路电压及小电流密度区间拟合精度低的缺点，对模型进行了改进。由于引入了损失电流密度，可拟合得到开路电压，且提高了小电流密度区间的拟合精度。

2 模型的建立

当外部电流密度(即实验测得电流密度)为0时，燃料电池处于开路状态，开路电压为：

EOCV=Erev-blg(jloss/j0)

(4)

将式(4)代入式(3)中，可得：

Ecell=EOCV+blg(jloss/j0)-blg[(j+jloss)/j0]

2.3 初产妇、经产妇妊娠期不同类型的UI构成比情况 经卡方检验，初产妇、经产妇妊娠期不同类型UI构成比差异有统计学意义（P＜0.001）。其中，初产妇与经产妇妊娠期SUI的患病率差异有统计学意义（P＜0.001），经产妇和初产妇UUI、MUI、OUI患病率，差异均无统计学意义（P＞0.05），见表1。

-Rj-mexp(nj)

(5)

整理后消去j0，得到改进后的半经验模型：

(6)

与Fraser模型相比，建立的半经验模型去掉了Erev，用EOCV代替；不需要获取温度、压强和浓度等其他数据来估算可逆电压。测得的开路电压可直接代入模型中，若实验中不能获得开路电压，只需将EOCV改为拟合参数即可。

3 模型的验证

实验使用由57片单体电池组成的7 kW车用PEMFC堆(大连产)，其中，质子交换膜的有效反应面积为312 cm2。

在六自由度振动台上进行振动实验，在G500测试平台(加拿大产)上测试性能。通过台架实验，实时检测燃料电池堆的输出电压和电流。采用阶跃方式对燃料电池堆进行加载，采集分布在0～1.4 A/cm2电流密度区间25个点的信息，记录每个电流点对应的电堆电压值。用电流中断测试法，得到燃料电池在部分电流下的欧姆阻抗。

电堆的极化曲线和欧姆阻抗见图1。

图1 电堆的极化曲线及部分电流密度下的欧姆阻抗

Fig.1 Polarization curves and Ohmic resistance at partial current density of cell stack

实验一共在14个电流密度下进行了电流中断测试，得到的欧姆阻抗在0.106 2 Ω·cm2和0.108 6 Ω·cm2之间，平均值为0.107 1 Ω·cm2。由此可知，电堆的欧姆阻抗在不同电流密度下的差别很小，可以认为：随着电流的变化，单体电池的平均欧姆阻抗基本保持不变。

实验过程中选取分布在整个电流密度区间内的25个点，分别代入式(1)、(3)和(6)中，拟合计算极化曲线的结果。3种模型拟合所得参数列于表1，极化曲线见图2。

表1 3种模型拟合所得参数对比 Table 1 Comparison of fitting parameters for three models

图2 3种模型拟合所得极化曲线 Fig.2 Fitting polarization curves for three models

从表1可知，3种模型的参数值在同一数量级。建立的模型拟合的确定系数R2为0.999 8，说明模型是合理的。

从图2可知，3种模型的拟合曲线基本都与实验数据一致，除了Kim模型拟合曲线在电流接近0时趋近于无穷大的区别，3条拟合曲线几乎一致。

3种模型拟合所得的极化曲线见图3。

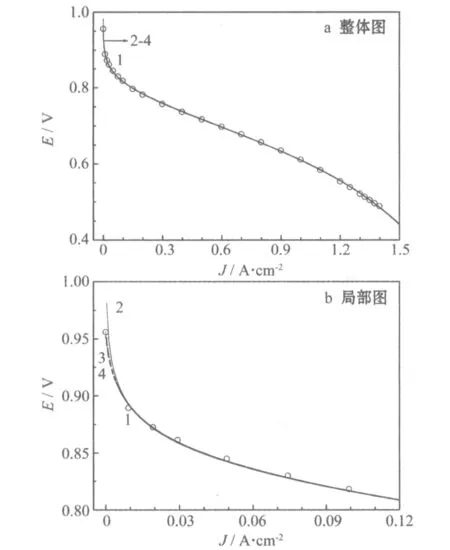
1 实验数据 2 Kim模型 3 Fraser模型 4 建立的模型

从图3可知，当电流密度为0～0.01 A/cm2时，Kim模型的拟合效果较差，与另外两条曲线差别明显。建立的模型在电流为0的时候逼近到实验测得的开路电压点,在规避了Kim模型不能在小电流密度区间拟合的缺点的同时，保留了Fraser模型整体拟合精度较高的优点，还可得到开路电压。

3.2 测试点电压的对比

将拟合参数值及实际电流密度(共25个点)分别代入式(1)、(3)和(6)，计算得到每个模型在各电流密度下的拟合电压值以及拟合值与实验值的偏差绝对值(见图4)。

图4 拟合值与实验值的偏差绝对值

从图4可知，3种模型在测试点的拟合电压值与实验值的偏差都在5 mV以内，当电流密度为0～0.5 A/cm2时，Kim模型的拟合精度最低。建立的模型的拟合精度与Fraser模型相比，在小电流密度区间高，在中、大电流密度区间几乎相同。

3.3 欧姆阻抗的验证

欧姆阻抗的验证有两个方面：①平均单体电池拟合值与57片单体电池拟合值的平均值的偏差越小，拟合效果越好；②平均单体电池拟合值和实验值的偏差越小，拟合精度越高。建立的模型拟合得到的单体电池的欧姆阻抗见图5。

图5 建立的模型拟合得到的单体电池的欧姆阻抗

从图5可知，单体电池的平均欧姆阻抗为0.116 3 Ω·cm2。由电堆极化曲线拟合得到的欧姆阻抗为0.111 2 Ω·cm2，电堆拟合值相对于57片单体电池拟合值平均值的偏差为-4.39%。由电流中断测试法可知，14个数据点测得的欧姆阻抗平均值为0.107 1 Ω·cm2，平均单体电池拟合值与实验测试平均值的偏差为3.83%，在允许的误差范围内，可认为建立的模型能够准确地反映电堆欧姆阻抗的变化特征。

4 结论

本文作者在总结大量燃料电池极化曲线经验或半经验模型的基础上，提出了一个半经验模型。

该模型结构简单，拟合参数较少，实验数据仅需要获取电堆电压和电流密度即可，并可在实验过程中直接测得，因此在实际中应用比较方便。与其他模型相比，优势主要体现在：拟合曲线非常逼近实测的开路电压点；提高了小电流区间的拟合精度。由燃料电池堆及单体电池的极化曲线拟合得到的欧姆阻抗都处在合理的范围内。此外，通过对比欧姆阻抗拟合值和断电流法测试值，可发现拟合精度较高。

[1] Kim J，Lee S，Srinivasan S，etal.Modeling of proton exchange membrane fuel cell performance with an empirical equation[J]. J Electrochem Soc，1995，142(8)：2 670-2 674.

[2] Chu D，Jiang R，Walker C.Analysis of PEM fuel cell stacks using an empirical voltage-current equation[J]. J Appl Electrochem，2000，30(3)：365-370.

[3] Fraser S D，Hacker V.An empirical fuel cell polarization curve fitting equation for small current densities and no-load operation[J]. J Appl Electrochem，2008，38(4)：451-456.

[4] Weydahl H，Moller-Holst S，Hagen Getal.Transient response of a proton exchange membrane fuel cell[J]. J Power Sources，2007，171：321-330.

[5] Poh C K，Lim S H，Pan H，etal.Citric acid functionalized carbon materials for fuel cell applications[J]. J Power Sources，2008，176：70-75.

Semi-empirical model improving for polarization curve of PEMFC

LI Ping1，TONG Xiao-min2，HAO Dong1，HOU Yong-ping1

(1.CleanEnergyAutomotiveEngineeringCenter，TongjiUniversity，Shanghai201804，China；2.ShanghaiMotorVehicleInspectionCenter，Shanghai201805，China)

Based on the measured data，the polarization curve characteristics of fuel cells were analyzed，the modeling methods were summarized.To raise low current density fitting accuracy and reduce fitting parameters，activation loss items were fixed，thereby an improved semi-empirical model derived from Kim model and Fraser model was proposed.The robustness and accuracy of fitting results of the three models were compared.The improved semi-empirical model had a better accuracy and higher practicality.

fuel cell； polarization curve； semi-empirical model

李 平(1992-)，男，安徽人，同济大学新能源汽车工程中心硕士生，研究方向：汽车试验技术，本文联系人；

国家自然科学基金(51275357)

TM911.41

A

1001-1579(2015)04-0179-03

2015-01-15

童晓敏(1968-)，男，上海人，上海机动车检测中心工程师，研究方向：新能源机动车检测技术，摩托车技术、标准等；

郝 冬(1988-)，男，天津人，同济大学新能源汽车工程中心博士生，研究方向：燃料电池，汽车试验技术；

侯永平(1971-)，男，山西人，同济大学新能源汽车工程中心教授，博士生导师，研究方向：汽车试验技术、车辆系统动力学等。