基于时间异质性的微博信息传播模型

吴联仁，李瑾颉，闫 强（.北京第二外国语学院酒店管理学院 北京 朝阳区 0004；.北京邮电大学经济管理学院 北京 海淀区 00876；3.圣母大学网络科学与应用跨学科研究中心 南本德 印第安纳州 美国 46556）

基于时间异质性的微博信息传播模型

吴联仁1，李瑾颉2，3，闫 强2
（1.北京第二外国语学院酒店管理学院 北京 朝阳区 100024；2.北京邮电大学经济管理学院 北京 海淀区 100876；3.圣母大学网络科学与应用跨学科研究中心 南本德 印第安纳州 美国 46556）

提出了具有时间异质性的SI（susceptible-infected）传播模型。通过构建异质的时间间隔序列，将微博信息传播动力学过程在无标度网络上仿真。研究结果发现信息新接受个体数n（t）以幂律形式减少，n（t）～t−β。与传统假设的时间间隔服从泊松分布的信息传播模型相比，时间间隔服从幂律分布的传播速度要缓慢很多。同时，传播动力学的幂指数β受行为时间间隔分布幂指数a影响，且具有关系β≈a−1。本文的仿真分析结果与理论预测结果一致。

BA网络；SI模型；传播动力学；时间异质性

传播动力学代表了许多真实的社会现象，如新兴传染病和信息流动，学者在这方面进行了多年的研究。传统的信息传播模型研究假设事件发生的时间和联系人的连接模式具有同质性［1］。最近学者针对经典传播动力学模型进行了改进，以说明社交网络的复杂连接模式［2］和非泊松特性的人类活动模式［3-8］。学者已经在具有连接异质性存在的情况下，对传播动力学进行了深入的研究，特别是在无标度网络中，P（k）～k−a，具有代表性的是万维网、合著者网络，以及许多其他社交网络［9-13］。

另一方面，时间异质性对人类行为的影响刚被认识。各种不同的人类活动方式，从电子邮件回复等待时间间隔、在线交易和网页访问的行为时间间隔、到及时通信行为时间间隔［14-16］，如果只考虑活动行为的时间，这些行为能够很好地用幂律的时间间隔分布来描述P（τ）～τ−a，τ表示连续两次行为的时间间隔。这些发现与传统的模型假设“人类行为时间间隔服从泊松分布”完全不同。人类行为的时间异质性是否影响信息传播的动力学？

微博作为为大众提供信息分享和交流的平台，其中的信息传播和网络结构得到了深入的研究［17-18］。本文以新浪微博为研究对象，认为转发和评论（一般评论后伴随着转发）是微博用户最常用的行为，研究微博用户转发、评论微博信息的时间特性是否影响微博信息的传播动力学。

本文基于对新浪微博数据的统计分析，建立基于时间异质性的微博信息传播模型，对模型的传播动力学给出理论分析；通过一种算法构造异质的时间间隔序列（即时间间隔序列服从幂律分布），再通过BA网络模型生成一个无标度网络，在无标度网络上进行信息传播模型仿真。

1 数据描述与分析

通过“网络爬虫”，以滚雪球抽样的方法抓取了新浪微博上某一热门话题中的所有参与用户和微博信息，一共搜集到175名用户和125 150条微博信息。这些信息总共被转发了2 260 826次，被评论了1 786 000次。收集数据的时间窗口是从2009年8月20日～2010年9月3日，共380天。针对每条信息，收集了信息ID、信息获得的转发数和评论数、信息被转发和评论的时间。收集了用户的ID、粉丝数、关注数和微博数。数据格式如表1和表2所示。

表1 信息数据格式

表2 用户数据格式

根据用户转发、评论微博的时间数据，研究用户连续两次行为的时间间隔。图1a描述的是群体层面，用户连续两次微博行为的时间间隔服从幂律分布，幂指数为2.5，并且具有明显的胖尾特征。与网页浏览、在线电影点播和社交网络中行为的时间间隔分布幂指数相近，都在1.0～3.0之间［19-20］。

以微博单位时间内获得的行为数（转发数与评论数之和）研究微博的传播情况。对125 150条微博进行筛选，选出获得行为数大于10的微博，总共有69 440条微博（微博获得的行为数太少，统计特征不明显）。以天为单位，统计每条微博每天获得的行为数，然后对69 440条微博在每天获得的行为数求平均值。微博每天获得的行为数分布情况如图1b所示。图中横坐标是时间，单位为天，纵坐标是微博获得行为数的均值。行为数以幂律形式消亡（幂指数β=1.5）。如果一个新的行为（转发或评论）认为是一个新感染个体（即一个新用户）在阅读微博后做出的行为，则微博信息新感染个体数n（t）以幂律形式减少，n（t）～t−β，β=1.5。幂指数β=1.5与图1a中用户行为时间间隔分布幂指数a=2.5相差为1。

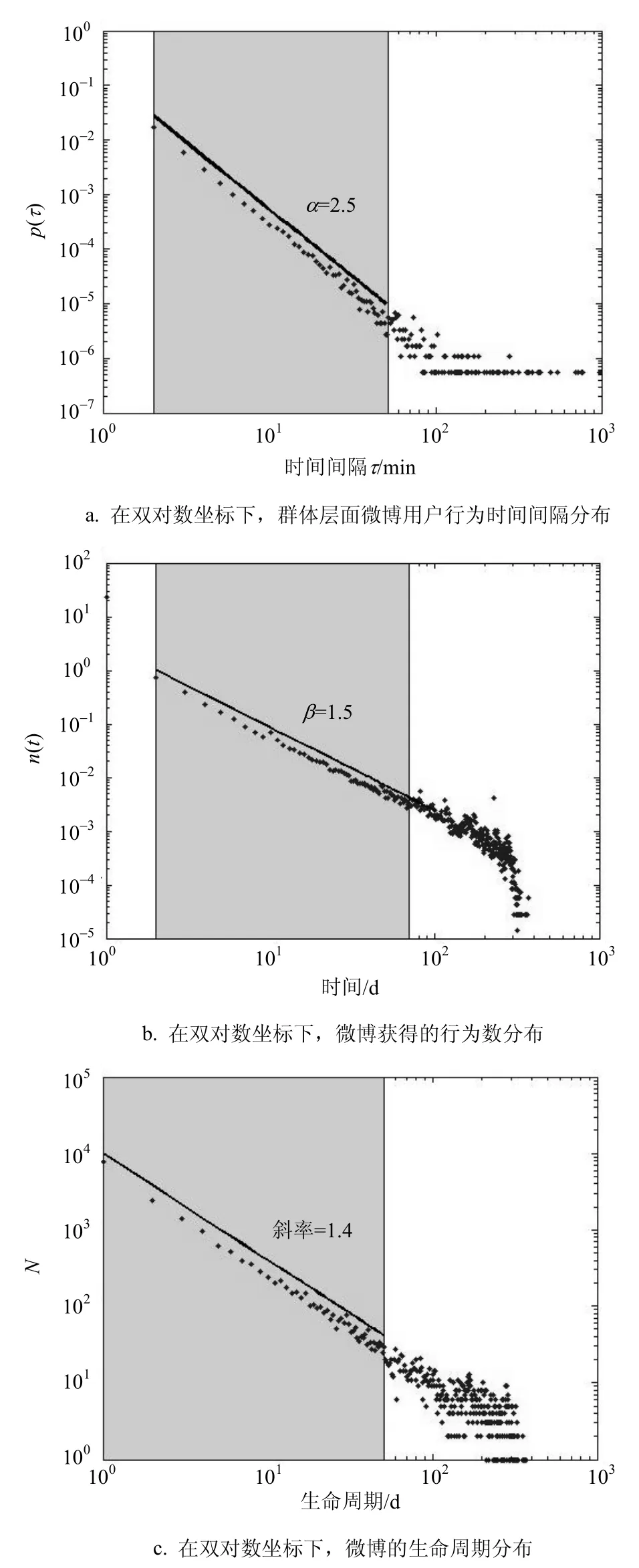
图1 新浪微博数据统计分析结果

图1c描述的是每条微博的生命周期。微博的生命周期指在数据收集时间窗口，微博首次发出时刻到最后一条与该微博相关转发或评论发出时刻的时间间隔。如图1c所示，横轴表示微博生命周期，单位为天。纵轴表示具有该生命周期的不同微博数N。微博生命周期服从指数为1.4的幂律分布，并且具有显著的胖尾特征。这说明大部分微博的生命周期很短，只有少部分微博具有长的生命周期，在微博社区中成为热点话题，具有较高的流行度。

2 模型建立

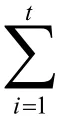
基于上述问题，对模型的描述如下。1）信息传播过程：在微博使用过程中，每个用户具有微博首页和个人页面两个列表。用户关注的对象如果发出信息，都将显示在微博首页上。因此，用户收到好友发送的信息存储在微博首页上，当用户打开微博查看信息时，就会对感兴趣的微博进行转发或评论。用户会以一定的概率转发收到的微博信息，转发信息存储在个人页面上。2）时间异质性：根据微博用户的实际使用情况，每个用户都有自己的习惯。因此，假设每个用户个体i具有一个固定的使用时间间隔τi，并且在群体层面用户行为（转发或评论行为）时间间隔服从幂律分布P（τ）～τ−a，2＜a≤3。当用户收到一条信息到将这条信息转发（或评论分享）出去的时间间隔称为转发信息的时间间隔，表示为Δ，则转发时间间隔分布记为g（Δ）～Δ−β。

基于上述模型的描述，本文提出的微博信息传播模型具有以下规则。1）假设网络中总共有N个个体，在时间步t=ti，随机选择一个个体i发出微博，其他个体对该微博信息均未知。2）个体j收到该微博，其中j∈δi，δi是个体i的邻居集合。对每个个体j，第一个转发时间步是tj0∈（ti，ti+τi）。并且时间步t=tj0+kτj，k=1，2，3，…都是j的转发时间步。其中τj是个体j的转发时间间隔。3）在每个转发时间步，个体j将以一定概率λ转发微博。如果个体j在tj时刻转发微博，可以得到j的微博转发时间Δ=tj−ti，并且满足Δ＜T，T表示微博在微博首页保留的时间上限。4）更新时间步t=tj，重复第2步到第4步直到设定的时间步。

3 理论分析

为了研究时间异质性对微博信息传播动力学的影响，本文提出了两个假设，并给出了相应的理论推导。

假设1：假设微博转发时间间隔服从幂律分布g（Δ）～Δ−β，并且1＜β＜2，则微博传播速度的消亡形式也服从幂律分布n（t）～t−β，并且具有相同的幂指数β。

证明：考虑传播过程的一般理论，假设传播过程在一个没有环形结构的网络上，并且在t=0时刻网络中只有一个感染个体，其他都是易感染个体。则在t时刻新感染个体的平均数可以表示为［21］：

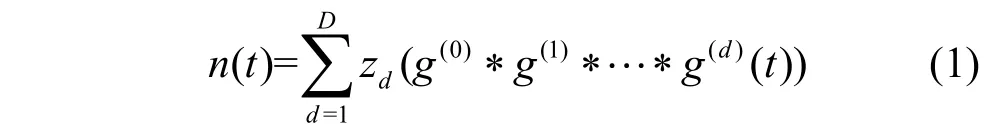
式中，zd表示在离初始感染节点第d步的平均易感个体数；D为d的最大值；∗表示卷积，如：

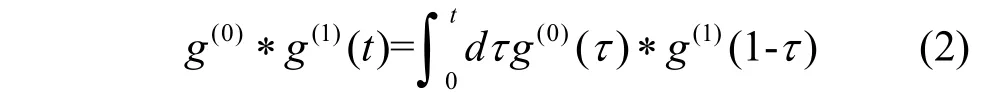
当1≪d时，可以得到：

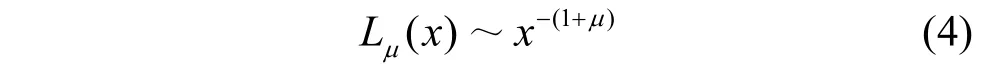
因此，式（3）为：

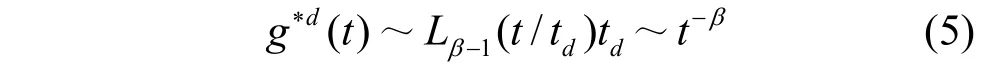
即：

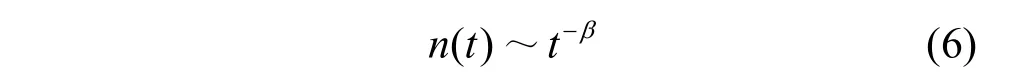
假设得证。

该假设表示如果微博转发时间间隔服从幂指数为β的幂律分布，则微博信息传播速度将服从同样的幂律分布。

假设2：假设个体行为时间间隔服从幂律分布P（τ）～τ−a，2＜a＜3，则微博信息传播速度的消亡形式服从幂律分布n（t）～t−β，1＜β＜2并且β=a−1。

证明：当个体行为时间间隔服从幂律分布P（τ）～τ−a，2＜a＜3，则时间间隔τi具有有限的平均值。

由于转发时间间隔概率密度函数与个体行为时间间隔概率密度函数有如下关系：

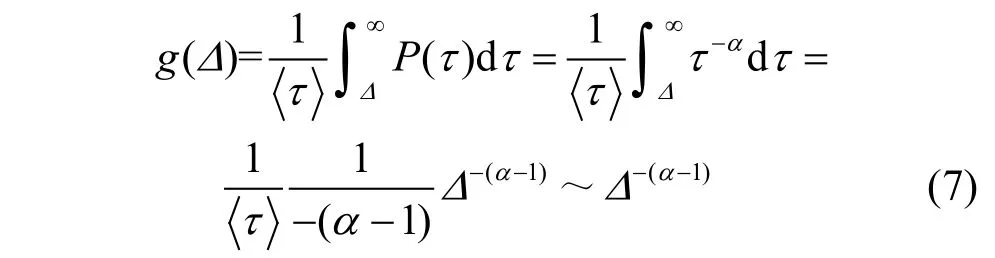
根据假设1可以得到：

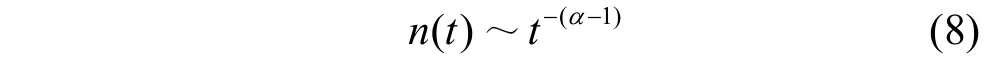
即：

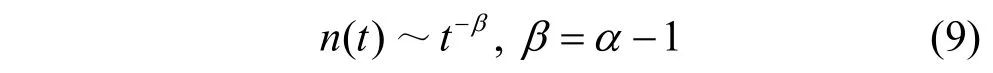
假设得证。

4 数值仿真与分析

4.1 异质时间间隔序列的构造

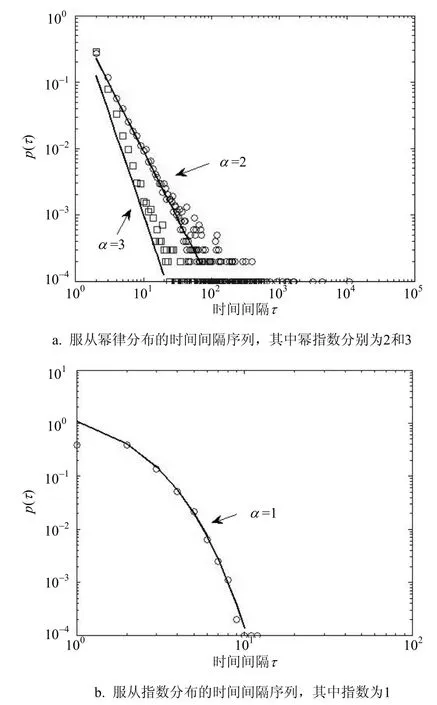
图2 构造的时间间隔序列

本文建立的模型需要给每个节点i分配一个固定的时间间隔τi，并且τi取自幂律分布P（τ）～τ−a。由于幂律分布在产生时间间隔时，可能会出现极大的值，因此需要事先对时间间隔τi设定一个上限M。即本文的目的就转变为生成一系列整数τ∈［1，M］，并且满足P（τ）～τ−a。根据文献［23］中提出的算法，在给定初值M和β，然后随机生成一个0～1之间的实数，就可以得到时间间隔序列τ，服从幂指数为β的幂律分布，且对任何β时间间隔序列τ具有相同的平均值。采用同样的方法，也可以产生服从指数分布P（τ）～τ−aτ的时间间隔序列。通过该算法获得的服从幂律分布和指数分布的时间间隔序列如图2所示。

在图2a中小圆圈代表的是幂指数a=2产生的时间间隔，小方块代表的是幂指数a=3产生的时间间隔。图2b中小圆圈代表的是泊松过程，时间间隔服从指数分布P（τ）～τ−aτ，并且指数a=1。在以上两种情况下，个体总数N=104，时间间隔的上限M=105。并且，获得的3个序列的时间间隔的平均值都为=1.96。

4.2 仿真与分析

在4.1节生成的时间间隔序列基础上，该小节首先通过Barabasi和Albert提出的BA无标度网络模型生成一个网络，仿真的微博信息传播过程在生成的网络上进行。网络节点总数量N=104，初始节点数N0=200，平均度=10，T=1 440，转发率λ=0.5。在每一个时间步，网络中添加一个新的节点来实现网络的连续增长，同时这个新的节点总是倾向于选择连接网络中旧节点中度较大的节点。模型的初始条件是：当t=0时随机选择一个感染节点，其他都是易感染节点。每个节点i给定一个固定的时间间隔τi，τi取自幂律分布P（τ）～τ−a，2＜a＜3。并且将时间间隔服从指数分布P（τ）～τ−aτ的情况加入到文中进行比较。模拟结果如图3和图4所示。

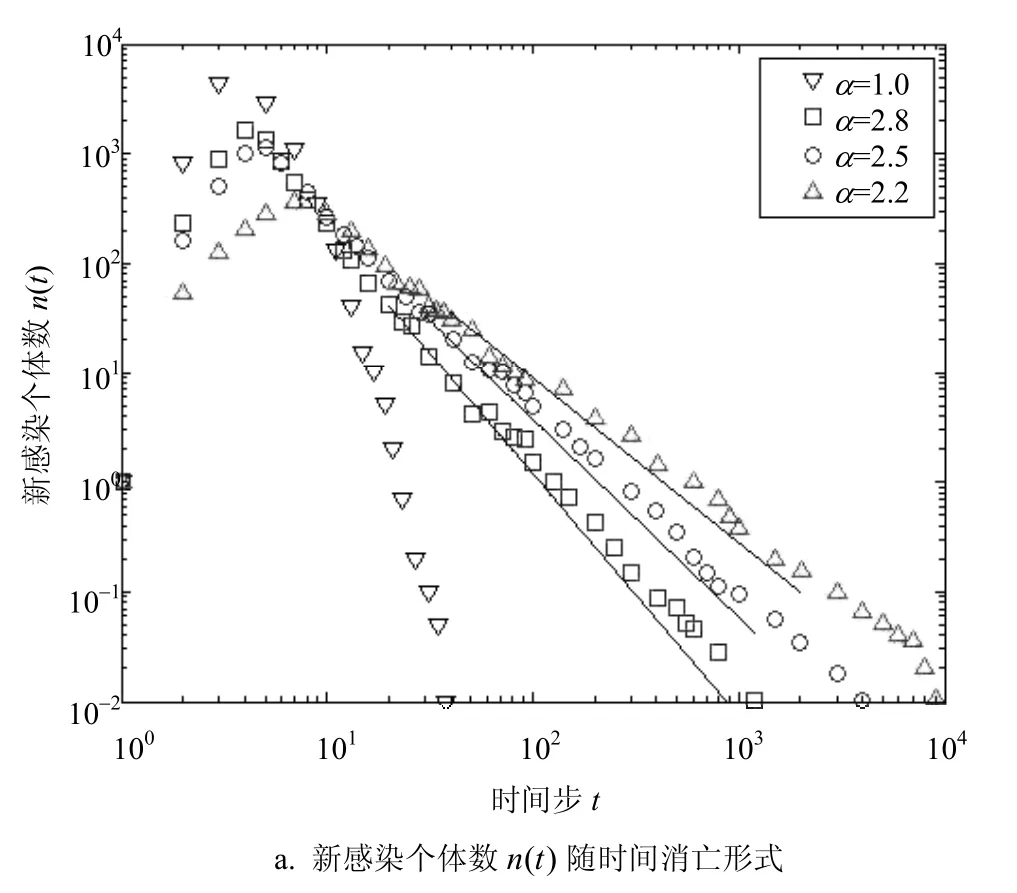
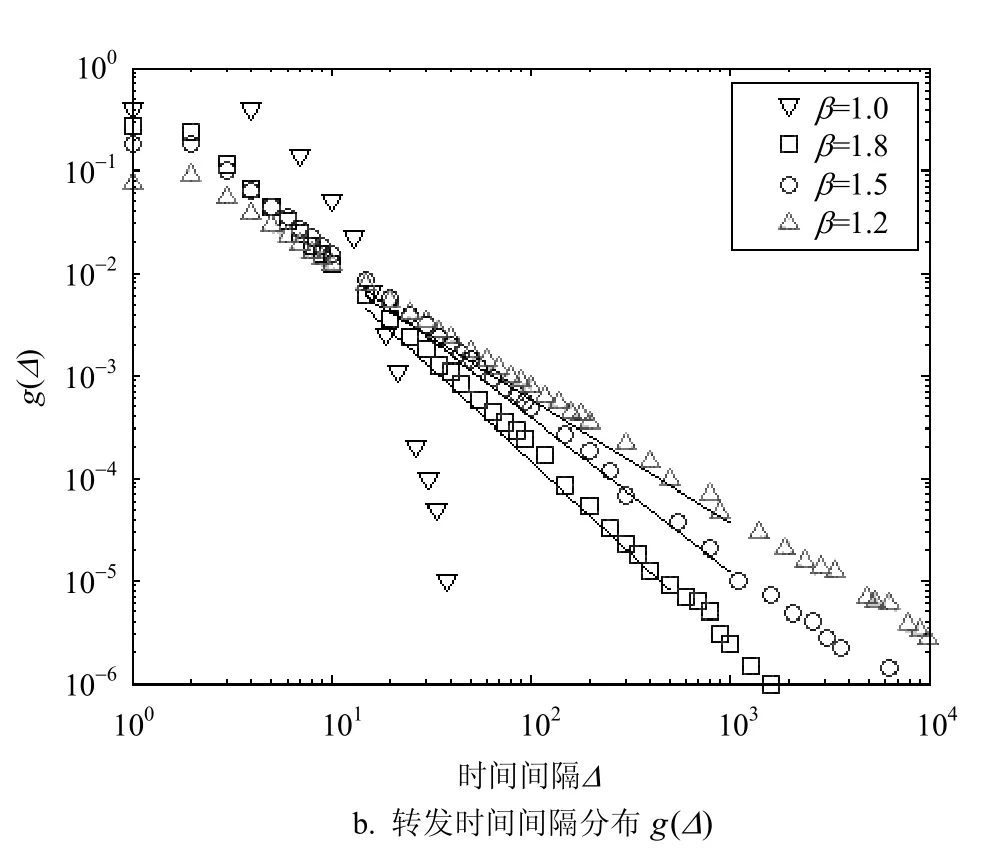
图3 数值仿真结果

图3a描述的是在初始只有一个感染节点的情况下，新感染个体数n（t）随时间消亡的形式，个体行为时间异质性幂指数分别为a=2.8、a=2.5和a=2.2的幂律分布P（τ），及a=1.0的指数分布，P（τ）～τ−aτ，所有分布P（τ）有相同的平均时间间隔=1.96。图3b所有个体行为时间间隔分布P（τ）对应的转发时间间隔分布g（Δ）。图中的连续直线分别是对应图形的拟合，两个图中的黑线斜率都分别近似等于−1.8，−1.5和−1.2，图中结果是2×103次独立运行的平均值。

从仿真结果看出在个体行为时间间隔服从幂律分布情况下新感染个体数n（t）和转发时间g（Δ）都服从幂指数为β≈a−1的幂律分布。新感染个体数和转发时间间隔与个体行为密切相关，表明个体行为对信息传播具有影响。个体行为的时间间隔幂指数越大，则新感染个体数n（t）消亡也越快。当个体行为时间间隔服从幂律分布，则新感染个体数n（t）也以幂律形式消亡。

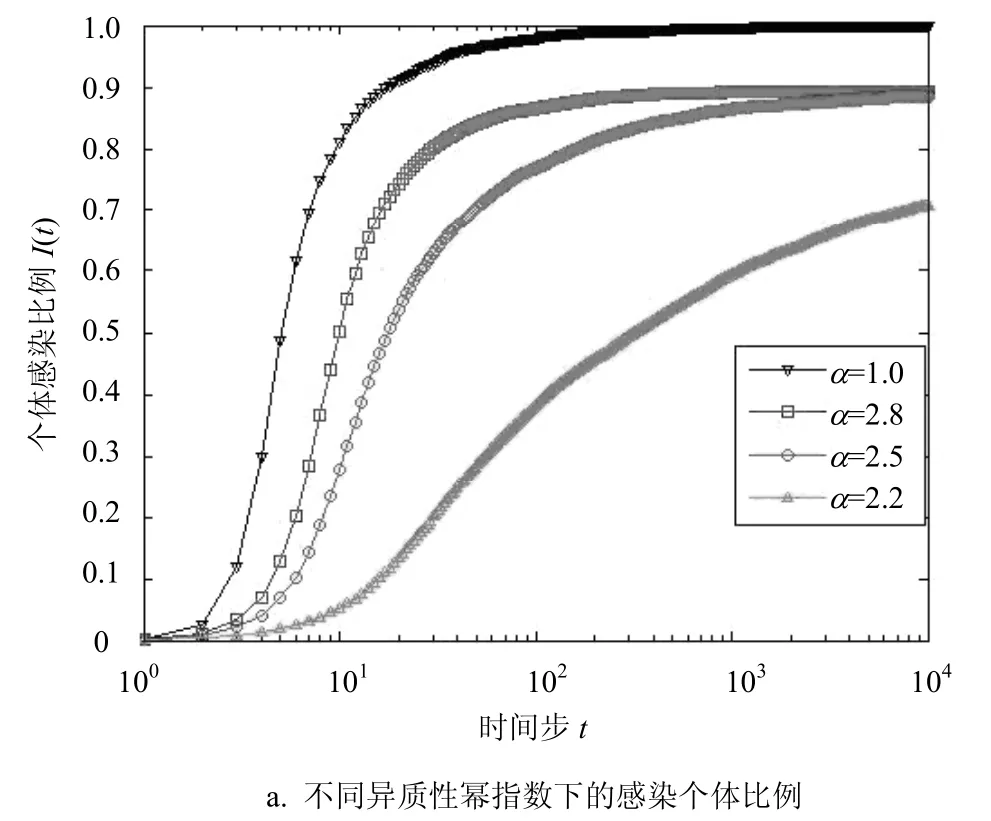
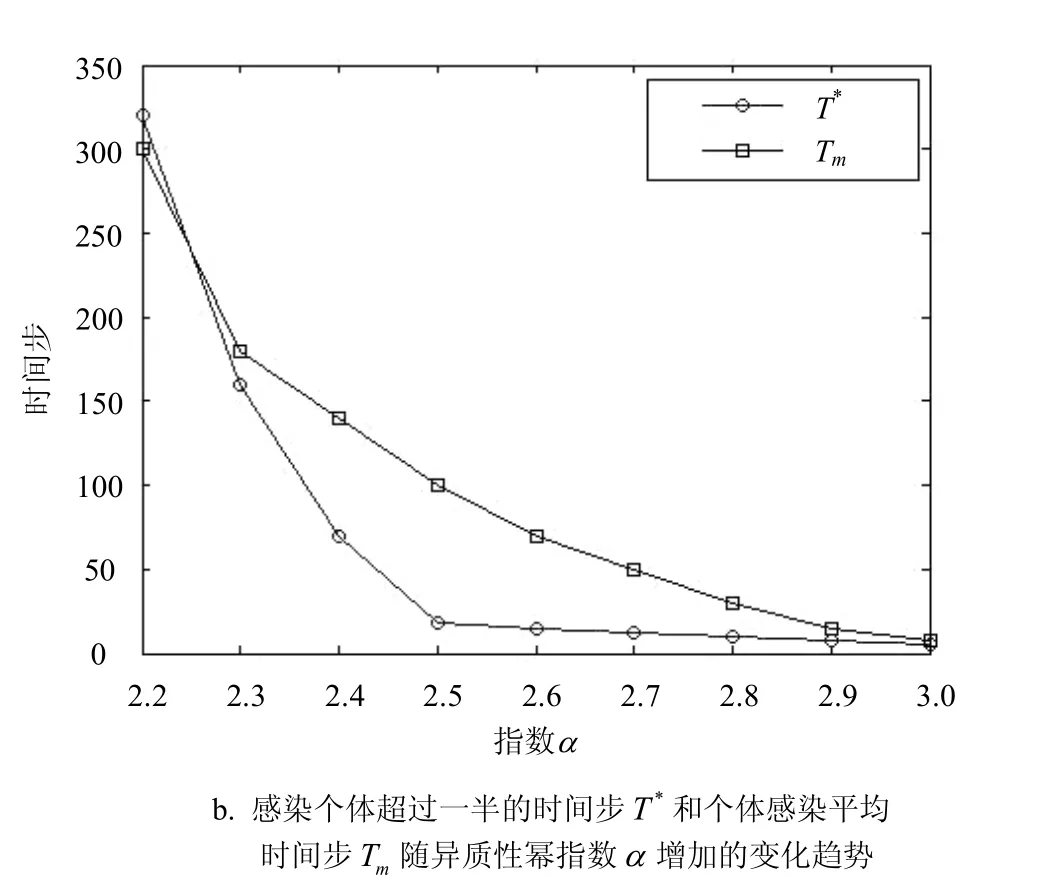
图4 数值仿真结果

图4a中显示了幂指数分别为a=2.8、a=2.5和a=2.2的幂律分布P（τ），以及a=1.0的指数分布，P（τ）～τ−aτ。从图4仿真结果可以看出，时间间隔分布幂指数a越小，时间间隔的异质性越大，信息传播的速度越慢，感染个体的比例也越低。且本文中时间间隔服从幂律分布的模型的信息传播速度显著地慢于时间间隔服从泊松布分的模型。

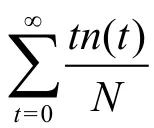
5 结论

微博系统下信息传播的影响因素有很多，例如微博网络的拓扑结构、个体行为的方式。国内外学者对异质的网络结构（如无标度网络、小世界网络）上的信息传播动力学进行了深入的研究。近年来，大量实证研究表明个体的活动行为具有时间异质性，这主要表现在不同个体对信息做出处理的等待时间不同，从而产生了服从幂律分布的行为时间间隔。通过实际微博数据统计分析说明异质的行为时间间隔对微博信息传播具有影响。

文章进一步提出了基于时间异质性的信息传播模型，强调了时间异质性对信息传播的影响。数值仿真结果和理论预测结果一致表明，先前假设传播时间间隔服从泊松分布的情况，其传播速度显著的快于时间间隔服从幂律分布的情况。并且个体行为模式对信息传播过程具有显著的影响，时间间隔分布幂指数越小，即时间间隔的异质性越大，信息传播的速度越慢，感染个体的比例也越低。

［1］DALEY D J，GANI J.Epidemic modeling：an introduction［M］.Cambridge：Cambridge University Press，1999.

［2］ALBERT R，BARABÁSI A L.Statistical mechanics of complex networks［J］.Review of Modern Physics，2002，74：47-97.

［3］BARABASI A L.The origin of bursts and heavy tails in human dynamics［J］.Nature，2005，435：207-211.

［4］KARSAI M，KIVELA M，PAN R K，et al.Small but slow world：How network topology and burstiness slow down spreading［J］.Physics Review E，2011，83：025102.

［5］张彦超，刘云，张海峰，等.基于在线社交网络的信息传播模型［J］.物理学报，2011，60（5）：050501.

ZHANG Yan-chao，LIU Yun，ZHANG Hai-feng，et al.The research of information dissemination model on online social network［J］.Acta Phys Sin，2011，60（5）：050501.

［6］SANZ J，FLORIA L M，MORENO Y.Spreading of persistent infections in heterogeneous populations［J］.Physics Review E，2010，81（5）：056108.

［7］MIN B，GOH K I，VAZQUEZ A.Spreading dynamics following bursty human activity patterns［J］.Physics Review E，2011，83（3）：036102.

［8］韩筱璞，汪秉宏，周涛.人类行为动力学研究［J］.复杂系统与复杂性科学，2010，7（2）：132-144.

HAN Xiao-pu，WANG Bing-hong，ZHOU Tao.Researches of human dynamics［J］.Complex System and Complexity Science，2010，7（02）：132-144.

［9］MIRITELLO G，MORO E，LARA R.Dynamical strength of social ties in information spreading［J］.Physics Review E，2011，83：045102.

［10］PASTOR-SATORRAS R，VAZQUEZ A，VESPIGNANI A.Dynamical and correlation properties of the Internet［J］.Physics Review Letter，2001，87（25）：258701.

［11］SANZ J，FLORIA L M，MORENO Y.Spreading of persistent infections in heterogeneous populations［J］.Physics Review E，2010，81（5）：056108.

［12］周涛，韩筱璞 闫小勇，等.人类行为时空特性的统计力学［J］.电子科技大学学报，2013，42（4）：481-540.

ZHOU Tao，HAN Xiao-pu，YAN Xiao-yong，et al.Statistical mechanics on temporal and spatial activities of human［J］.Journal of University of Electronic Science and Technology of China，2013，42（4）：481-540.

［13］李楠楠，周涛，张宁.人类动力学基本概念与实证分析［J］.复杂系统与复杂性科学，2008，5（2）：138-143.

LI Nan-nan，ZHOU Tao，ZHANG Ning.Concept and empirical results of human dynamics［J］.Complex Systems and Complexity Science，2008，5（2）：138-143.

［14］GONCALVES B，RAMASCO J J.Human dynamics revealed through web analytics［J］.Physics Review E，2008，78（2）：026123.

［15］RADICCHI F.Human activity in the web［J］.Physics Review E，2009，80（2）：026118.

［16］LESKOVEC J，HORVITZ E.Planetary-scale views on a large instant-messaging network［C］//Proceedings of the 17th international conference on World Wide Web.Beijing，China：ACM，2008：915-924.

［17］陆豪放，张千明，周莹，等.微博中的信息传播：媒体效应与社交影响［J］.电子科技大学学报，2014，43（2）：167-173.

LU Hao-fang，ZHANG Qian-ming，ZHOU Ying，et al.Information spreading in microblogging systems：Media effect versus social impact［J］.Journal of University of Electronic Science and Technology of China，2014，43（2）：167-173.

［18］邵凤，郭强，曾诗奇，等.微博系统网络结构的研究进展［J］.电子科技大学学报，2014，43（2）：174-183.SHAO Feng，GUO Qiang，ZENG Shi-qi，et al.Research progress of the microblog system structures［J］.Journal of University of Electronic Science and Technology of China，2014，43（2）：174-183.

［19］周涛.在线电影点播中的人类行为动力学模式［J］.复杂系统与复杂性科学，2008，5（1）：1-5.

ZHOU Tao.Human activity pattern on on-line movie watching［J］.Complex Systems and Complexity Science，2008，5（1）：1-5.

［20］赵庚升，张宁，周涛.网页浏览中的标度行为研究［J］.统计与决策，2009，277（1）：18-19.

ZHAO Geng-sheng，ZHANG Ning，ZHOU Tao.Scaling behavior of web browsing［J］.Statistics and Decision，2009，277（1）：18-19.

［21］VAZQUEZ A.Polynomial growth in branching processes with diverging reproductive number［J］.Physics Review Letter，2006，96（3）：038702.

［22］FELLER W.An introduction to probability theory and its applications［M］.New York：Wiley，1967.

［23］YANG Zi-mo，CUI Ai-xiang，ZHOU Tao.Impact of heterogeneous human activities on epidemic spreading［J］.Physica A，2011，390（23）：4543-4548.

编辑 蒋 晓

Micro-Blog Information Spreading Model Based on Temporal Heterogeneity

WU Lian-ren1，LI Jin-jie2，3，and YAN Qiang2
（1.School of Hospitality Management，Beijing International Studies University Chaoyang Beijing 100024；2.School of Economics and Management，Beijing University of Posts and Telecommunications Haidian Beijing 100876；3.Interdisciplinary Center for Network Science and Applications，University of Notre Dame South Bend Indiana USA 46556）

A susceptible-infected（SI）spreading model with temporal heterogeneity is proposed.By generating heterogeneous time-interval sequence，the spreading dynamics processes are simulated on scale-free networks.The results show that the number of new infectionsn（t）decays with a power law，n（t）～t−β，leading to extremely slow prevalence decay.And the power-law exponent in the spreading dynamicsβis related toa，β≈a−1.These observations are well supported by both the theoretical predictions and simulation analysis.

BA networks；SI model；spreading dynamics；temporal heterogeneity

TP391

A

10.3969/j.issn.1001-0548.2015.05.003

2014-06-06；

2015-06-16

北京市社科基金项目（13KDB011）

吴联仁（1985-），男，博士，主要从事社交媒体、信息传播方面的研究.