黏性对深水波列非线性演化的影响

张本辉， 蔡 烽， 杨 波， 吴 明， 董东东(海军大连舰艇学院 航海系， 辽宁 大连 116018)

黏性对深水波列非线性演化的影响

张本辉， 蔡 烽， 杨 波， 吴 明， 董东东
(海军大连舰艇学院 航海系， 辽宁 大连 116018)

修正的四阶非线性薛定谔方程(mNLS)所建立的数值模型能有效模拟深水波列的非线性演化，但当演化距离较长时，需考虑黏性衰减作用。在mNLS方程的基础上添加一个黏性修正项，建立更加完善的数值模型。模拟边带扰动初始条件下深水波列的演化，并对该过程中谱成分能量的变化进行分析，进而研究水池宽度、载波波陡、载波频率和尺度因子对深水波列非线性演化能量衰减的影响。

船舶工程； 四阶非线性薛定谔方程； 黏性； 非线性演化； 数值模拟

随着我国经济和综合国力显著提升、海外利益不断拓展，国家对海洋越来越关注。与此同时，伴随着我国海军逐步从近海走向远洋，维护海洋权益的使命变得日益沉重。在我国海军“走出去”的过程中，海浪环境深刻影响着舰艇的航行和作战效能，因此更加准确地把握远洋海区风浪环境的特点和规律，对提升我国海军的战斗力而言具有重要意义。

目前，从流体力学基本方程出发，大多数深水波浪数值模拟都是基于线性海浪模型进行的。近些年来大量的外海观测和实验室试验均已证明实际的海浪是非线性的，主要表现在波高的非瑞利分布、双峰乃至多峰海浪谱的大量存在、波浪变形和破碎以及海浪的非线性局域化特征等几个方面。[1]随着海洋科技发展和海洋工程需求日益迫切，线性海浪模型已不能满足越来越高的精度要求，因此对海浪的非线性进行研究得到了众多海洋科技工作者的关注。[2]研究能反映海浪非线性特征的数值模拟方法[3]是未来的发展趋势，使用非线性演化理论来模拟深水海浪将变得更加合理、有效。

Stokes波对于缓慢调制的周期性(边带)扰动而言是不稳定的，BENJAMIN和FEIR对论证事实做了关键性的工作，初步证实了深水波列传播过程中的演化具有不稳定性，且在波陡明显小于碎波条件下也会发生，这一点与真实深水波浪的情况较吻合，对该问题进行研究有助于了解实际海面上波群的形成与演化特性。[4]ZAKHAROV，BENNEY和ROSKES基于窄谱假设和弱非线性假设推导了描述表面振幅包络波演化的三阶非线性薛定谔方程，该方程具有波陡的三阶精度，比较适合描述具有较小波陡(<0.1)的波列演化;而对于较大的波陡，其模拟结果只是在波列演化的初期符合实际情形，无法准确模拟长时间的波列演化。为进一步克服三阶方程的不足，DYSTHE[5]考虑由辐射应力引起的平均流效应，推导出了四阶Dysthe方程；LO等[6]397对Dysthe方程进行小的修正，得到了mNLS方程，该方程所预测的边带稳定性和不稳定边带增长率在波陡<0.3时均与精确结果非常接近;张运秋等[7-8]则通过mNLS方程来研究深水波列的演化和畸形波的生成。mNLS方程是由基于势流理论的拉普拉斯方程组推导得到的，但是对于深水波列长时间非线性演化而言，黏性衰减影响非常重要，因此在mNLS方程的基础上添加一个黏性修正项，从而建立更加完善的数值模型，对边带扰动初始条件下深水波列的非线性演化进行模拟。

1 深水波列的数值模型

1.1控制方程

通常海面上的波浪运动在无黏无旋条件下可通过速度势函数的拉普拉斯方程和自由表面、海底等边界条件来描述，利用泰勒级数展开，将自由面边界条件展开到O(ε4)四阶形式(波陡ε=ka，k和a分别为载波波数和波幅)。经推导可得到群速度移动坐标系统下的四阶非线性薛定谔方程[6]398为

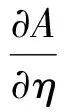
(1)

(2)

A(0,η)=A(2π,η)

(3)

A(0,z,η)=A(2π,z,η)

(4)

1.2黏性修正模型

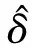
(5)

式(5)中：B为水槽宽度，当B→∞时，可理解为壁面边界层的黏性不作考虑;μ为黏性衰减系数，则考虑黏性修正之后的控制方程(式(1))就变为

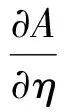
(6)

1.3离散步长的虚拟频谱方法

对于NLS方程而言，可利用逆散射变换求取其精确的解析解。四阶非线性薛定谔方程通常不适合于解析求解，因此不得不借助于各种数值算法。离散步长的虚拟频谱方法是一种有效求解mNLS方程的数值求解方法，主要分为虚拟频谱方法和中心有限差分法两部分。虚拟频谱方法是一种以傅里叶变换为基础的方法，需满足式(3)和式(4)，可有效求解mNLS方程的线性部分。在深水波浪传播过程中，线性与非线性是同时作用的，但在数值计算中，需将两者分开求解，仅考虑非线性作用(线性项为0)，则式(6)简化为

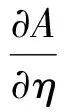
(7)

仅考虑线性作用(非线性项为0)，则式(6)简化为

(8)

复波包A(ξ,η)(0<ξ<2π)的傅里叶空间上的变换和逆变换为

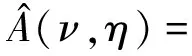
(9)

(10)

式(9)～式(10)中：v=0,±1,±2,…,±N;2N为周期2π上的离散点数;Δξ=π/N;当ν≠±N时，μν=1；当ν=±N时，μν=1/2。

在每一个空间步长上，首先将非线性部分的解作为线性部分的初值代入并求解，从而得到下一步方程的解；然后把线性部分的结果代入非线性部分方程，从而依次递进求解。

2 数值仿真及讨论

2.1初始条件

TULIN等[11]认为试验水池中的调制分为2种：一种由背景噪声扰动引起；另一种被强制加载在造波机上，既可随意改变边带频率，又可改变初始边带的振幅和调制的剧烈程度。背景噪声对波列调制演化有较大影响，而边带扰动波列则可最大程度地消除背景噪声的影响。[12]因此，模拟中采用载波加一对边带扰动形成的复波包作为初始条件，即

A(ξ,0)=1+S(eiξ+e-iξ)eiα

(11)

式(11)中：S和α分别对应着边带的初始振幅和相位，这里载波的基频取2 Hz，初始振幅S=0.05。根据Dysthe的不稳定性标准，取边带扰动的初始相位α=-π/4时，可在短时间内获得最大线性的增长。

2.2深海波列的非线性演化过程分析

仿真中,取波陡ε=0.15，尺度因子λ=0.775;当考虑黏性时，假设水池宽度B=1 m;在实验室水池中，一般取μ=1×10-6m2/s。此时可得到初始波列复波包络的非线性时空演化(见图1)。

从图1中可看出：在复波包振幅非线性演化过程中，时而高高耸起形成尖峰，时而迅速下降形成深深的波谷，大的波包近似周期性出现；但是，在考虑黏性的情况下，复波包振幅整体上出现了一定的降低，且这种趋势随着演化距离的增大而更加明显，这与实际水槽中的波列演化效果是一致的。在初始阶段，不稳定增长率比能量衰减率大时，有可能出现畸形波，之后由于能量的衰减，很可能不会出现严格满足畸形波定义的大波。就畸形波的形成而言，这是考虑黏性与否最大的不同。

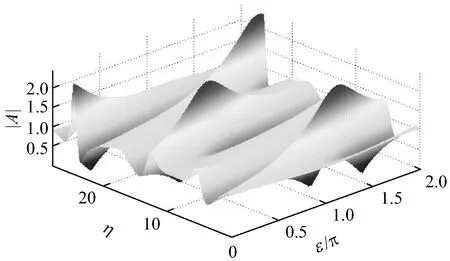
a) 不考虑黏性

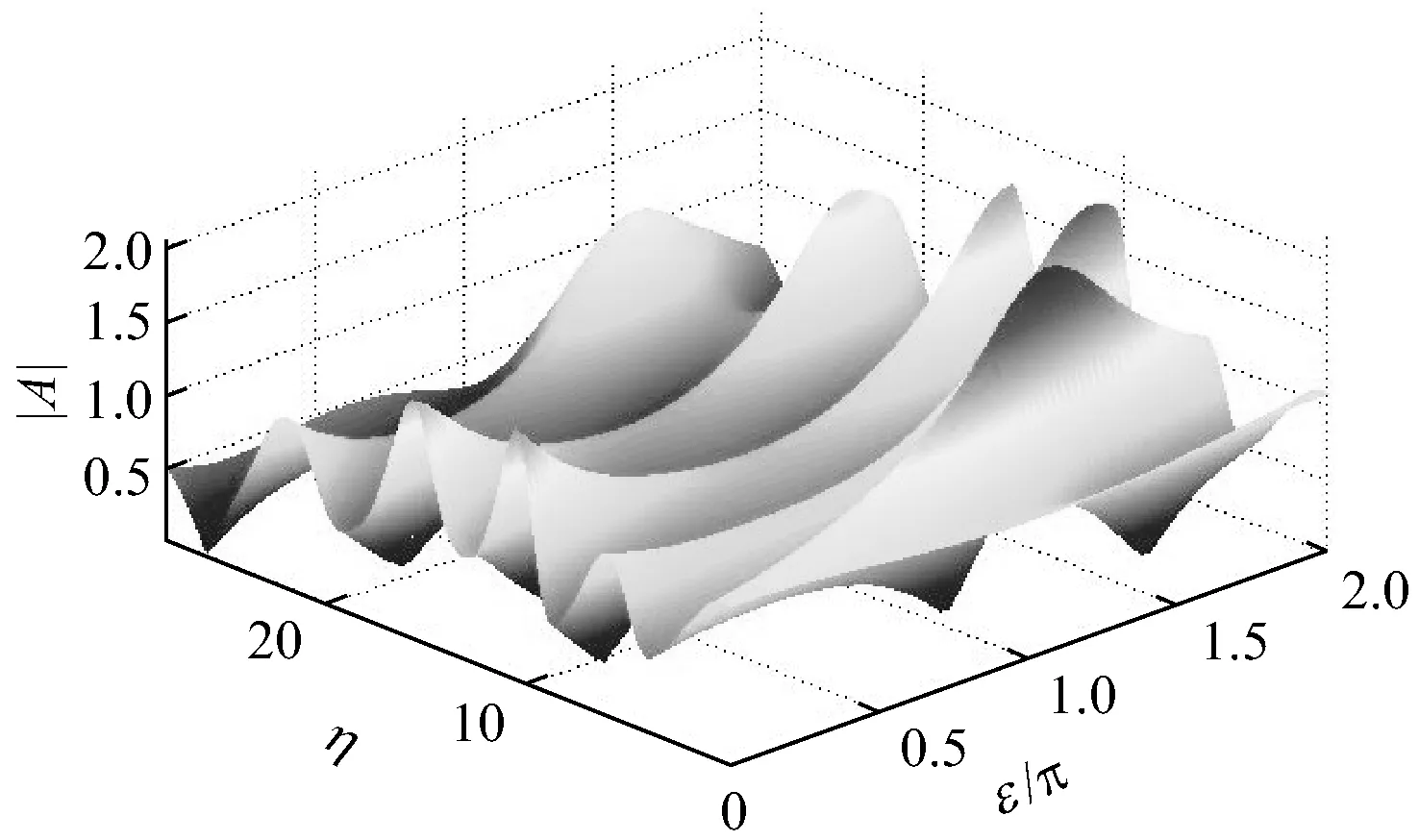
b) 考虑黏性

演化过程中，复波包振幅的变化是由其内在能量的演化决定的，图1对应的复波包谱成分能量变化见图2。

b) 考虑黏性

由图2可知：载波v=0及不稳定边带v=±1,±2的谱成分能量曲线也是以一种类周期的方式增长和衰减的，载波谱振幅快速下降处，不稳定边带谱成分能量快速上升，载波的能量迅速转移到不稳定边带中，此时对应的图1中的包络幅值在短时间内迅速增高；但是，在考虑黏性的情况下，缩短了能量在谱成分之间转移的演化距离，且载波和边带中的总能量在传递过程是逐渐衰减的。在不考虑黏性的情况下，能量相对误差随演化距离的变化见图3。

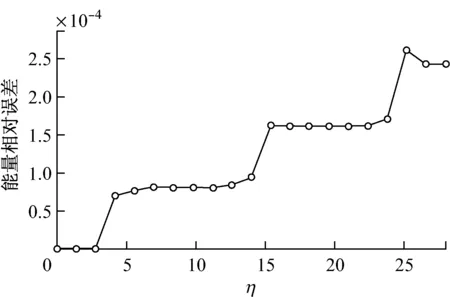
图3 不考虑黏性情况下能量相对误差随演化距离的变化

由图3可知：能量相对误差在整个演化过程中不断增大，最大值为2.6×10-4，说明演化过程中满足能量守恒定律，确保了整个模拟的有效性。在考虑黏性的情况下，包络总能量在演化过程是逐渐衰减的，则包络总能量随演化距离变化的对比见图4。

由图4可知，在考虑黏性的情况下，包络的总能量随演化距离的增大而衰减得非常明显。因此，包络总能量可看作是衡量黏性衰减对深水波列非线性演化影响强弱与否的一项重要指标。

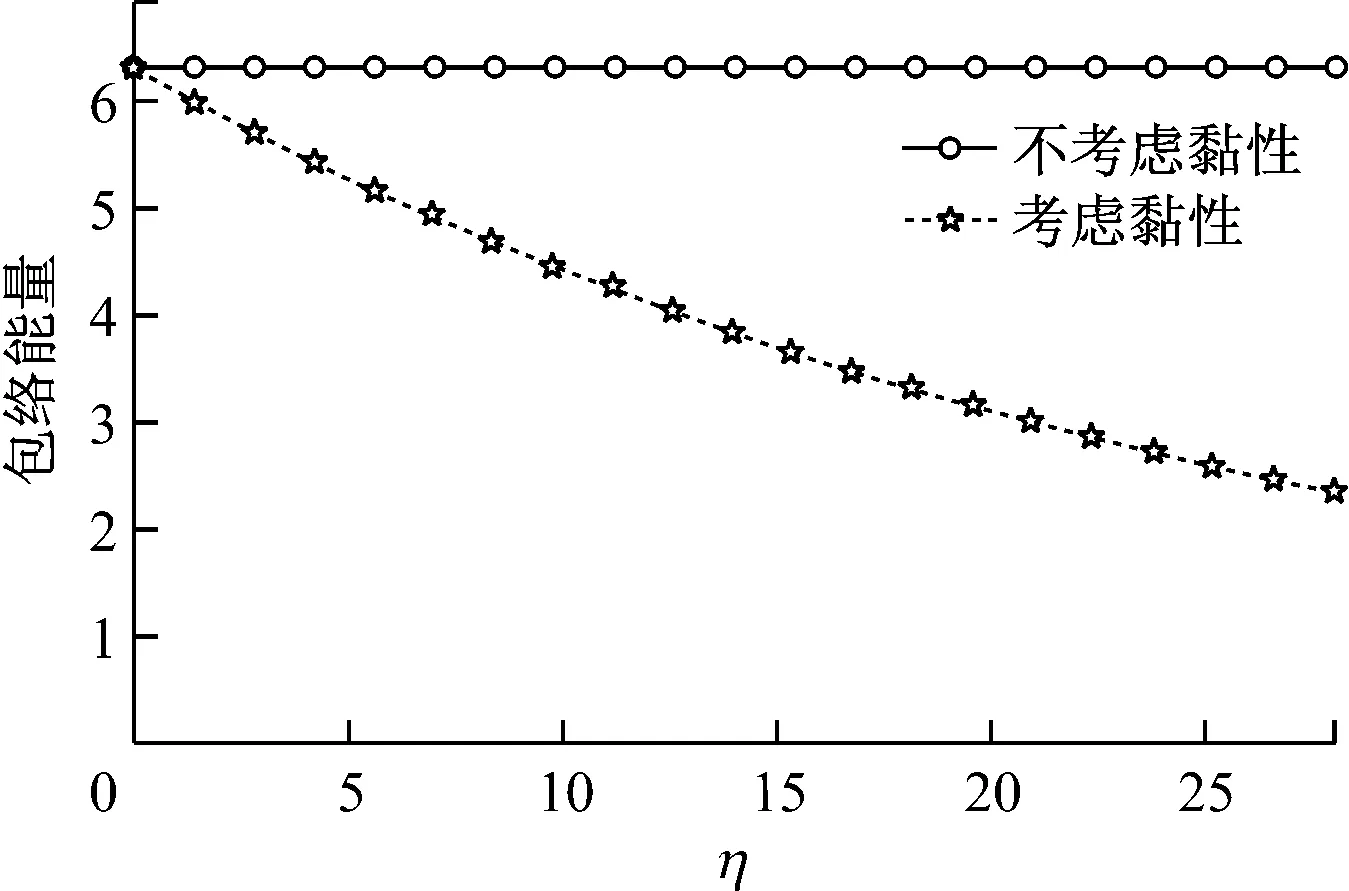
图4 包络总能量随演化距离变化的对比

2.3考虑黏性情况下深水波列非线性演化过程中能量衰减的影响因素分析

在黏性修正的mNLS方程数值模型的基础上，输入的初始条件若与“2.1”相同，则采用单一变量法，依次分析水池宽度、载波波陡、载波频率和尺度因子的改变对深水波列非线性演化过程能量衰减的影响(见图5)。

a) 水池宽度

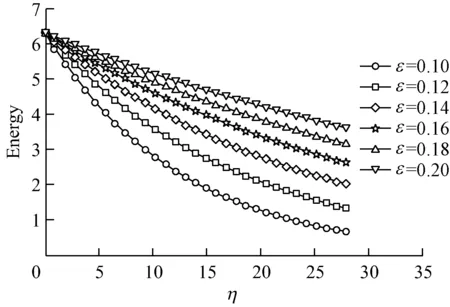
b) 载波波陡

c) 载波频率

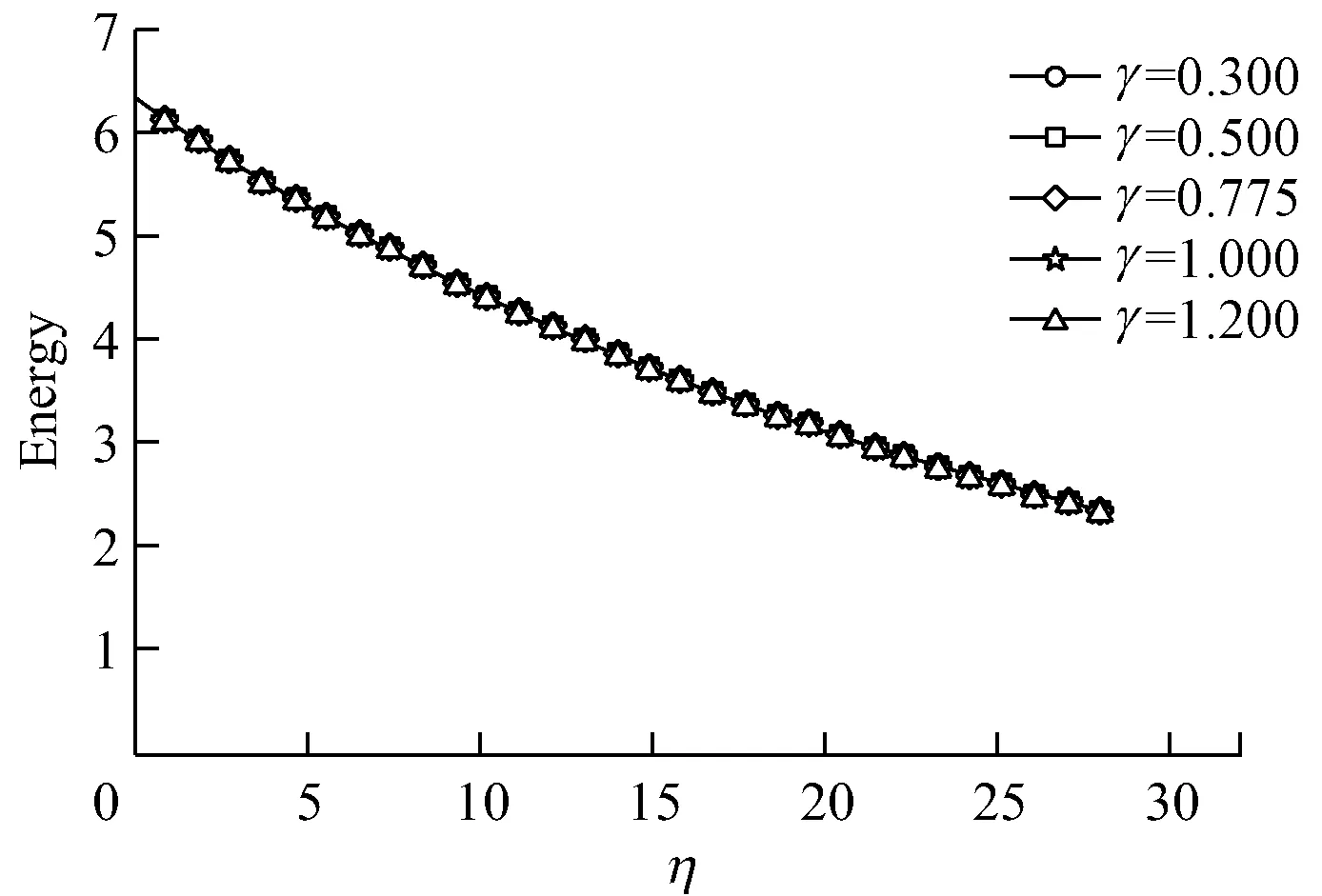
d) 尺度因子

由图5可知：总体而言，由于黏性衰减的作用，总能量随着演化距离的增大而逐渐减少；水池宽度对能量衰减的影响最大，载波波陡和载波频率次之，尺度因子的影响相对较小；随着载波波陡和载波频率增大，相同演化距离上总能量的衰减逐渐减小。

进一步的研究表明：虽然黏性很小的流体在没有边界的地方像无黏性的流体，但因摩擦的关系而在壁面上形成了一个薄的“边界层”，且在该层中，速度从相应于无黏性流体运动的数值变化到流体黏性粘附在边界层上所应有的数值，黏性越小，该边界层就越薄。因此，无论水池壁宽度如何，只要水的黏性和速度不变，形成的薄的边界层及其对靠近壁面部分的水波影响就是一致的，只不过水池越宽，对远离壁面的水波影响就越小，对整个水池中水波总的能量影响也相对越弱，相同演化距离上总能量的衰减也就越小。当水池宽度B在20 m以上时，总能量的衰减就会比较小，但考虑到模型的1+1维单方向性，水池宽度又不能太宽，因此需综合把握。

3 结束语

基于添加黏性修正项的mNLS方程，模拟边带扰动情况下深水波列的非线性演化，分析水池宽度、波陡、载波频率和尺度因子对深水波列演化过程中能量衰减的影响，得到以下结论。

1) 黏性作用会对深水波列的非线性演化产生重要影响，能量转移循环出现的演化距离缩短的同时伴随着包络能量的衰减。

2) 水池宽度对能量衰减的影响最大；载波波陡和载波频率次之，尺度因子相对较小。

以上只是基于黏性修正的数值模型进行的仿真，可为水池试验提供一定的理论指导。后续需根据实际水池试验或CFD数值波浪水池的数据进行进一步的验证。

[1] 蔡烽,缪泉明,顾民,等. 海浪的非线性效应及其产生原因[J].中国造船,2006,47(Z1):153-159.

[2] 蔡烽,沈泓萃,缪泉明,等. 海浪非线性行为的参数化表征[J].船舶力学,2008,12(2):157-167.

[3] 聂卫东,康凤举,褚彦军,等.基于线性海浪理论的海浪数值模拟[J].系统仿真学报,2005,17(5):1037-1039.

[4] 胡凯程.深水非线性波列调变之数值解析[D].台南:国立成功大学,2004.

[5] DYSTHE K B.Note on a Modification to the Nonlinear Schroedinger Equation for Application to Deep Water Waves[J]. Proceedings of the Royal Society of London, 1979,369:105-114.

[6] LO E, MEI C C.A Numerical Study of Water-Wave Modulation Based on a Higher-Order Nonlinear Schroedinger Equation[J]. Journal of Fluid Mechanics,1985,150:395-416.

[7] 张运秋,张宁川,裴玉国.畸形波数值模拟的一个有效模型[J].大连理工大学学报, 2008, 48(3):406-410.

[8] 张运秋.深水畸形波的数值模拟研究[D].大连:大连理工大学,2008.

[9] CHU V H, MEI C C. The Nonlinear Evolution of Stokes Waves in Deep Water[J].Journal of Mech.1971,47:337-351.

[10] SEGUR H. Viscous Decay of Envelope Solitons in Deep Water Waves[J].Phys.Fluids.1982,24:2372-2374.

[11] TULIN M P, WASEDA T. Laboratory Observations of Wave Group Evolution, Including Breaking Effect [J] Fluids Mech,1999,378:197-232.

[12] 张威.非线性波浪调制演化的实验研究[D].大连：大连理工大学,2012.

ViscosityEffectonNonlinearEvolutionofDeep-WaterWaveTrains

ZHANGBenhui,CAIFeng,YANGBo,WUMing,DONGDongdong
(Navigation Department, Dalian Naval Academy, Dalian 116018, China)

A numerical wave model based on the modified fourth-order nonlinear Schrodinger equation (mNLS) is good for describing the evolution of deep-water wave envelope, however, viscous attenuation effect needs to be taken into account when evolution distance is relatively long. A viscous modifying term is added to the mNLS governing equations to construct an improved numerical model, which works better in simulating nonlinear evolution. The evolution of deep-water under the sideband disturbance conditions are simulated and the energy variation of spectral components is analyzed. The energy damping in the nonlinear evolution of deep-water wave trains is investigated through varying the parameters: the pool width, the carrier wave steepness, the carrier wave frequency, and the scale factor.

ship engineering; fourth-order nonlinear Schrodinger equation; viscous effects; nonlinear evolution; numerical simulation

2015-04-29

十二五预研项目(51314030101)； 大连市科技基金(2012J21DW027);海军大连舰艇学院科研发展基金(DJK201422)

张本辉(1988—),男,河南南阳人，博士生,研究方向为非线性海浪及舰船耐波性。E-mail:fengdeyingzi123@163.com

1000-4653(2015)03-0061-04

U661.1

A