物理运动平台的三维视景补偿算法

陈国权， 尹 勇, 李丽娜， 杨神化(. 大连海事大学 航海动态仿真与控制行业重点实验室， 辽宁 大连 606；. 集美大学 航海学院， 福建 厦门 360)

物理运动平台的三维视景补偿算法

陈国权1,2， 尹 勇1, 李丽娜2， 杨神化2
(1. 大连海事大学 航海动态仿真与控制行业重点实验室， 辽宁 大连 116026；2. 集美大学 航海学院， 福建 厦门 361021)

为使船舶操纵模拟器更具真实感，在现有航海模拟器架构上增加电动杆驱动的物理运动平台，构建半物理运动平台驱动的船舶操纵模拟器。主要解决船舶操控仿真平台中船模集成、船模解算坐标与电动平台坐标系同步以及因电动平台限位而需进行的视景补偿等算法的研究与实现等问题。实际集成与测试结果表明，该方法可行。

船舶工程； 船舶智能操控仿真平台； 电动杆驱动； 坐标系统匹配； 视景补偿； 三维仿真

现代航海模拟器自诞生至今， 经历了从简单到复杂、 从单一到综合的发展历程。20世纪 80年代以来，计算机成像(Computer Generated Image，CGI) 生成视景技术的采用， 不仅使航海模拟器经历了从“盲” ( 无视景， 仅凭仪器操纵) 到 “可视”( 有视景， 能创建一种逼真的操作环境)的变革，而且使航海模拟器与飞行模拟器一起成为了虚拟现实系统成功应用的范例。[1]类似的半物理平台[2-4]已得到长足发展，但随着模拟器不断普及，使用者对航海模拟器提出了更高的要求，纯视景的航海模拟器仍停留在视觉的感受上，已无法满足当前的需求。

物理驱动平台(如电动平台)的引入可更加有效地增强用户的操纵体验[5]，但在研究实现小型船舶的物理运动仿真平台时发现，小型船舶的转动运动幅值通常较大，而物理仿真平台通常会出于安全和稳定性考虑设置运动幅度限定，此时完全依赖物理仿真平台的运动不能完全与船舶的真实运动相匹配。鉴于此，引入三维视景补偿算法。

1 船舶运动建模机理和实现

1.1建模的3套坐标体系

船舶数学运动建模通常提供惯性坐标系和附体坐标系(船体坐标系)2种形式的坐标体系。两者之间的相互转换关系模型[6-7]为

(1)

(2)

(3)

(4)

式(1)～式(4)中：φ，θ和ψ为欧拉角；u，v和w分别为附体坐标系下船舶的前进、横移和垂荡速度；p，q和r分别为附体坐标系下船舶的横摇、纵摇和艏摇角速度。船体六自由度信息具体可描述为：前进、横荡和垂荡为船体在XYZ轴上的平动效果；横摇、纵摇和艏摇为船体绕XYZ轴的转动效果。船模解算库支持输出惯性坐标体系和体坐标系下的六自由度船模运动信息。在船体坐标体系下，船纵剖面(艏艉方向)为X轴，且艏部方向为正；船横剖面(左右舷方向)为Y轴，且右舷方向为正；与船体水线面垂直的法线方向为Z轴，且指向海底的方向为正。

1.2船舶运动数学建模的基本原理

船舶操控仿真平台围绕特殊船(如小型游艇)展开，其核心模块之一是船舶运动解算数学模型[8]，考虑船舶航行环境中的各个方面的因素。

船舶运动数学建模的基本原理[1-2]为

(5)

式(5)中：m为船体质量；(xG,yG,zG)为船体的重心位置；(u,v,w)为船体的平动速度；(u°,v°,w°)为船体的加速度；(p,q,r)为船体的转动速度；(p°,q°,r°)为船体的转动加速度；(Ix,Iy,Iz)为船体轴向上的转动惯性矩;(Iyz,Izx,Ixy)为船体某两个轴耦合的惯性矩(如耦合转动惯量)；(X,Y,Z)为作用在船体上的外部合力；(K,M,N) 为作用在船体上的外部力矩。

船舶在旋回中会产生较大的横倾角，图1和图2为某游艇在3 m浪高、15 m/s风速条件下全速右满舵和全速左满舵的横倾角变化曲线。

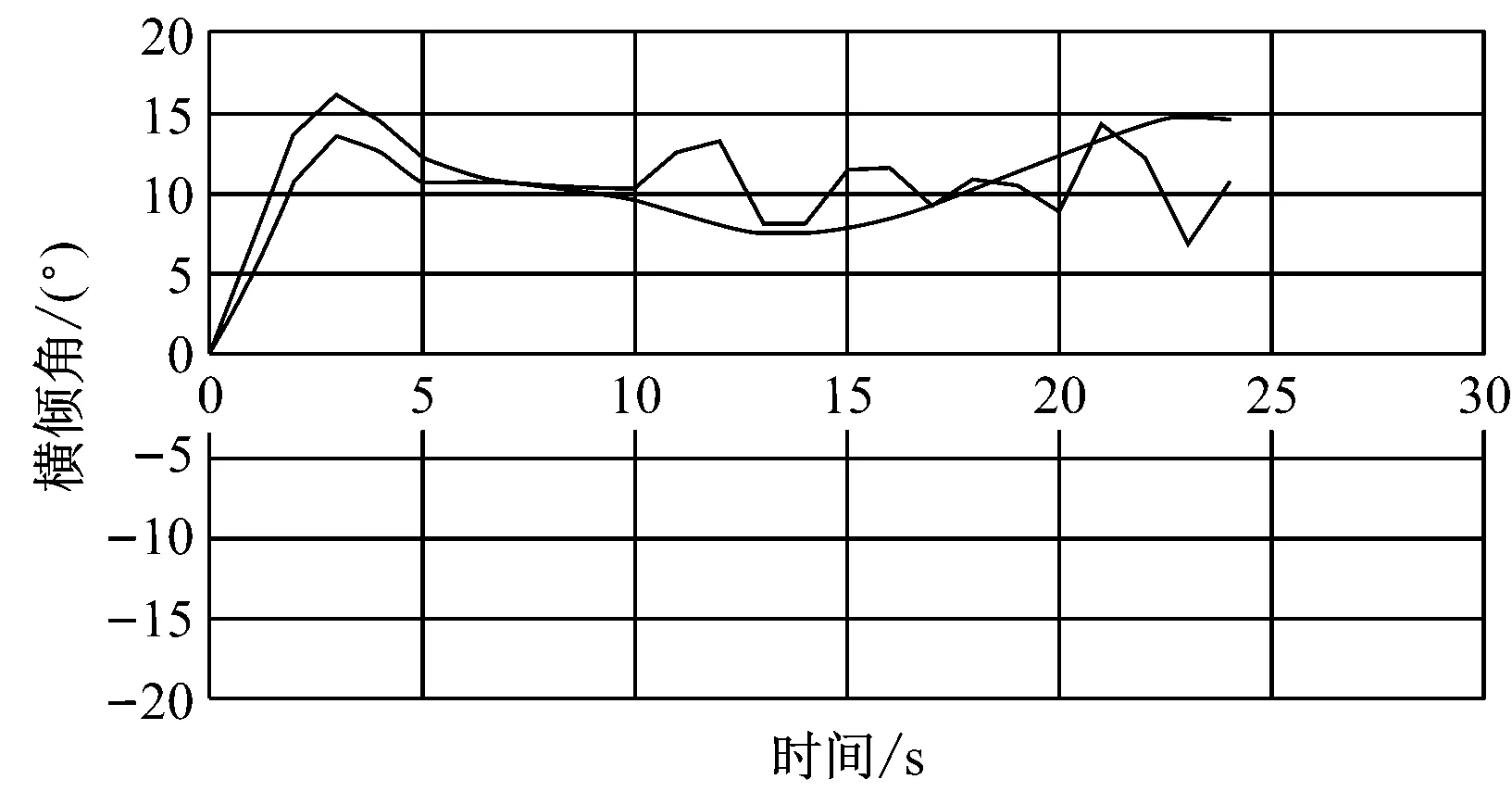
图1 全速右满舵旋回下横倾角变化曲线

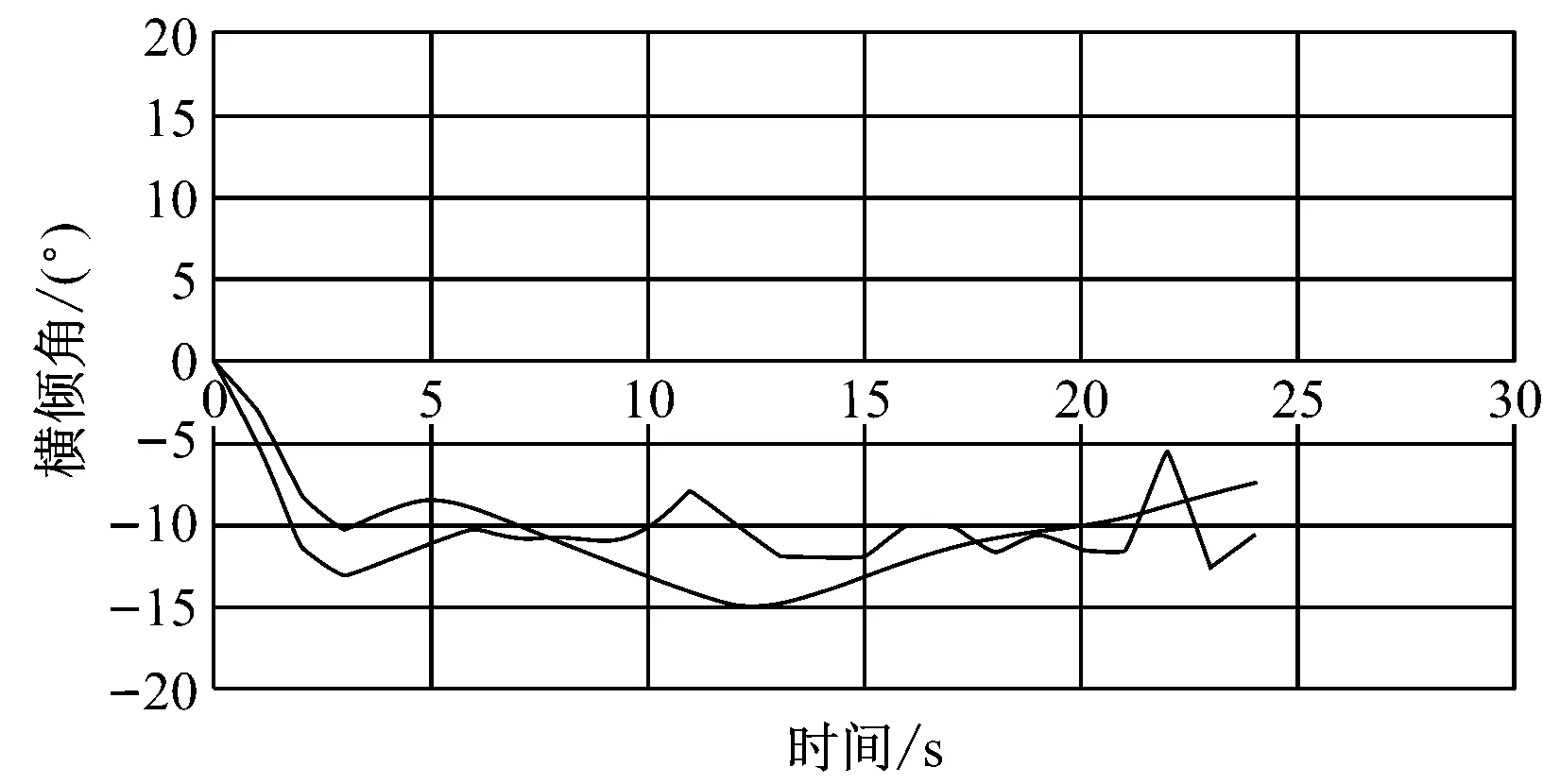
图2 全速左满舵旋回下横倾角变化曲线

从图1和图2中可发现，该游艇产生最大达15°的横倾角。

2 电动杆平台驱动原理与视景补偿系统

2.1电动杆驱动的硬件组成

船舶三自由度运动平台由PLC控制箱柜和三自由度电动运动平台组成(见图3)。其工作原理为：应用工业计算机将船模解算平台中计算的目标中心点空间位置Z及夹角α和β输入PLC控制箱柜微机，自动计算出各伺服缸的目标位移；控制器通过位置闭环以用户设定的速度到达模拟平台目标姿态。系统选用高性能的伺服运动控制器满足模拟平台的快速运动和响应要求。 三自由度平台可实现沿Z轴(垂直轴)的移动及绕X轴和Y轴(水平轴)的转动，可模拟刚体在空间的受限运动状态。三自由度平台实现的沿Z轴的移动即为船舶运动中垂荡的效果，绕X轴和Y轴的转动即为船舶运动中横摇和纵摇的效果。

电动杆驱动的船舶操控仿真平台建立在船舶操纵模拟器的基本架构上，增加了三自由电动杆驱动控制模块。其基本工作原理为：三自由度电动控制柜是三自由运动平台的核心部件，主要通过工业标准中的Modbus通信协议接收来自上位机的运动信息并驱动三自由度运动平台实体；三自由度运动实体平台主要用于接收来自三自由度电动控制柜的控制信息并驱动电动杆模拟三自由运动姿态。

图3 三自由度运动平台

2.2电动杆驱动数据解算原理与上位机通信原理

电动杆驱动硬件仿真平台由1#杆、2#杆和3#杆等3根运动杆组成，通过输入船舶运动三自由度信息(即垂荡、横摇和纵摇)反算实体平台运动杆长度。详细算法[9-10]为

式(6)～式(8)中：L1，L2和L3分别为1#杆、2#杆和3#杆的设定长度；φ为横摇角；θ为纵摇角；Z为垂荡幅度值；R为平台结构固定参数值，本系统中取值为150 mm。系统初始化后，上位机会通过Socket主动连接PLC控制柜；系统运行后，由上位机船模解算的数据便会实时输入到下位机控制箱，控制箱通过PLC控制器控制驱动电动实体运动平台。

2.3电动驱动平台和视景补偿的机理与实现

船舶运动为六自由度数学运动模型，可输出船体在XYZ轴上的平动效果和船体绕XYZ轴的转动效果。电动平台的机械设计限定了运动实体只能实现横摇、纵摇和垂荡等3个自由度的运动，剩余的3个自由度的运动必须通过三维视景系统加以补偿体现。为实现视景系统与三自由度实体运动平台的结合，需要以解决视景系统、船模输出和三自由度运动平台解算之间的坐标系统的问题及运动平台机械保护和运动限制的问题为前提。

1) 视景系统采用惯性坐标系、船模解算出来的接口数据可输出3种坐标系数据，船模提供的标准接口是EA坐标系(即惯性坐标系)下的船体六自由度运动信息。

2) 全仿真船舶操纵模拟器视景只有与电动平台联合才能构建真正意义上的六自由度半物理运动仿真平台，即3物理运动+3虚拟场景运动。

3) 为有效保护实体平台的稳定性、解决其固有的机械限位问题，必须引入视景补偿机制。

为解决视景和物理平台之间的相互补偿问题，制定全仿真船舶操纵模拟器视景和电动平台联合运动策略表(见表1)。

表1 全仿真船舶操纵模拟器视景和电动平台联合运动策略表

物理电动平台的本体因机械限制和保护电动杆等原因，在工作状态下横摇的最大幅度为左右10°，纵摇的最大幅度为前后10°，垂荡的最大幅度为上下80 mm，同时伴有横摇、纵摇和垂荡等耦合运动。因此，为保护电动平台并延长其使用寿命、保证训练学员的安全，需进一步限定横摇、纵摇和垂荡的幅度值。目前限定电动平台的横摇最大值和纵摇最大值为5°，垂荡最大值为50 mm。由于船模输出的数据值会超出这些限定值(比如小型船舶在高速航行中操满舵时会使横倾最大至15°左右(如图1和图2所示)，遇到风浪时可能会更大直至出现翻船的情况)，且电动平台只能体现船舶运动的3个维度上的运动信息，因此提出视景补偿的基本概念算法。电动杆驱动游艇运动与视景补偿原理图见图4。

图4 电动杆驱动游艇运动与视景补偿原理图

1) 图4中的U，V，W，R，P和Q分别为船舶的前进、横荡、垂荡、横摇、纵摇和艏摇等6个自由度的信息。

2) 对于U，V和Q(即前进、横荡和艏摇运动)，受平台的限制，将直接输入到三维视景驱动模块中。

3) 对于W，R和P(即横摇、纵摇和垂荡运动)，在不超出电动物理平台限定值的情况下，直接输入到三自由度控制箱，并通过PLC电路驱动物理电动平台。

4) 若W，R和P中的任意一个或多个超出限定值，则需进行视景的补偿处理。其补偿处理方式为：W-50 mm =W′;R-5°=R′;P-5°=P′。

5) 若需要视景补偿，则最后体现在视景中经过坐标转换之后的视坐标六自由度信息为U′,V′,W″,R″,P″和Q′，相应的坐标转化公式如式(1)～式(4)。

3 船舶运动模型的系统集成

基于电动杆平台驱动和OSG视景驱动[11]的船舶操控仿真平台通过引入物理电动平台，能有效增强操船的真实感、提升训练人员的操纵乐趣。基于半物理仿真的船舶模拟器将虚拟现实和物理运动平台有机结合在一起，能让用户切身体会到航行的真实感。船舶在航行中的横摇、纵摇和垂荡等运动姿态会对船舶操纵人员的生理和心理产生影响，引入物理仿真机构大大提升了船舶模拟器的航行操纵真实性。船舶操纵模拟器引入视景和电动平台需考虑的一个问题是某些小船(如游艇)在高速和大舵角情况下行驶或在大风浪情况下行驶时会有很大的横倾角，由于物理机械上的限位及出于保护电机和运动杆强度考虑，需对电动动作部分运动幅度进行一系列限制。因此，需在仿真环节引入视景补偿算法，游艇的六自由度运动有策略性地分为视景驱动和电动杆驱动两部分，从而真正实现运动解算和电动运动与视景补偿的统一。

在有效解决船舶运动视景与真实电动平台的坐标统一和视景补偿后，即可将三自由度运动平台增加到船舶操控仿真平台中。具体做法为：将三自由度控制箱连入交换机中，为更好地完成视景补偿效果，目前采用的方式是将三自由度控制箱通过TCP/IP网络通信协议与视景端机连接，而本船端与视景机端已在原有架构上连接，船模解算的六自由度信息已通过UDP广播至视景机端，视景机端已通过TCP/IP与三自由度控制箱相连，在每个时隙里视景端都会比较电动三自由度的实际姿态决定是否需要视景补偿。最后经过集成的整套系统见图5。

图5 电动杆驱动游艇仿真实物与电子海图显示

4 结束语

通过认真分析船模、视景和三自由度运动平台的坐标体系以及研究三自由度平台与视景间的姿态补偿，基本实现了基于三自由度电动平台驱动的船舶操控仿真平台，有效增强了船舶运动仿真的操船真实感和使用者的航行体验感。

[1] 金一丞, 尹勇. STCW公约与航海模拟器的发展[C]// 全国防止船舶航行事故新经验新技术学术研讨会, 2004.

[2] 吴海彬. 基于半物理仿真的海上平台沉浮运动研究[D]. 杭州：浙江大学, 2002.

[3] 陈小亮. 基于VxWorks的船舶运动半物理仿真系统平台的设计与实现[D]. 哈尔滨：哈尔滨工程大学, 2011.

[4] 杨灏泉, 赵克定, 吴盛林,等. 飞行模拟器六自由度运动系统的关键技术及研究现状[J]. 系统仿真学报, 2002, 14(1):84-87.

[5] 延皓. 基于液压六自由度平台的空间对接半物理仿真系统研究[D]. 哈尔滨：哈尔滨工业大学, 2007.

[7] FOSSEN T I. Marine Control System [M]. Trondheim: Marine Cybernetics, 2002：10-12.

[8] 张显库，贾欣乐. 船舶运动控制[M]．北京：国防工业出版社，2006:14-15.

[9] 姜虹, 贾嵘, 董洪智,等. 六自由度并联机器人位置正解的数值解法[J]. 上海交通大学学报, 2000, 34(3):351-353.

[10] 徐炜. 基于Pro/E和ADAMS的三自由度运动平台仿真分析[J]. 现代制造工程,2010(8):69-72.

[11] 王锐，钱学雷. OpenSceneGraph三维渲染引擎设计与实践[M]. 北京:清华大学出版社, 2009:168-171.

3DSceneCompensationAlgorithmforPhysicalMotionPlatform

CHENGuoquan1,2，YINYong1,LILi’na2,YANGShenhua2
(1. Key Laboratory Marine Dynamic Simulation & Control for Ministry of Communications, Dalian Maritime University, Dalian 116026, China;2. Navigational College， Jimei University, Xiamen 361021, China)

The electric driven ship motion simulation platform is developed for the current navigational simulator to be mounted on to enhance the realty of the ship handling simulation. The following issues are solved: to integrate ship mathematical motion model with the present navigational simulator, to synchronize the ship model calculation output, the 3D visual scene and the electric driven platform; and to adapt the 3D visual scene to the motion limitation of the platform . Tests indicate that the proposed method is feasible.

ship engineering; intelligent ship handling and control platform; electric putter; coordinates match; visual compensation; 3D simulation

2015-05-11

国家自然科学基金(51109090; 60774066)

陈国权(1981—)，男，浙江诸暨人，讲师，博士生，主要从事船舶航行自动化及仿真方面的研究。E-mail:cgq0802@foxmail.com

尹 勇(1969—)，男，湖北郧县人，教授，博士生导师，主要研究方向为实时图形算法、虚拟现实技术、航海仿真技术及多通道视景系统等。E-mail:bushyin@163.com

1000-4653(2015)03-0057-04

TP391.9

A