基于分散模型的混凝土流动机理研究
张 雄,赵 明,季 涛,张永娟
(1.同济大学 材料科学与工程学院,上海 201804;2.同济大学 先进土木工程材料教育部重点实验室,上海 201804)
混凝土的工作性,尤其是流动性的设计是现代混凝土配合比设计中重要的组成部分.合适的流动性设计方法能够在原材料的选择、配合比最优化设计上起到指导作用,而建立系统化的流动性设计理论模型是规范配合比设计的前提,在此基础上才能在材料变化、时间变化、环境变化时对混凝土性能进行准确判断[1],这对混凝土工业的自动化可起重要作用[2].
混凝土是一种多相非均质复杂材料,基于组成、结构与性能的材料学在对其进行研究过程中,建立了3种结构模型:第1种是以颗粒堆积理论为支撑,将混凝土性能研究转化成各组成材料的最优化堆积问题[3].这种方法能较好解释细颗粒组分对混凝土性能提高的作用[4].但是,混凝土各组分之间尺寸变化非常大,堆积算法无法区分堆积密度的贡献作用.第2种方法是利用水泥净浆、砂浆以及混凝土的几何相似性,建立模型化的流变参数方程[2,5-6].该方法是利用相对简单的净浆或砂浆来模拟研究复杂的混凝土[1,6],如CEM[7]方法.然而,水泥净浆、砂浆、混凝土的流动机理尚不明确,简单的模型化可能造成较大的偏差.第3种为分散模型,将混凝土视为固体材料(分散相)分散在黏性液体(介质相)中,其性质会受介质相性质的影响[5,8-11].该模型将复杂的混凝土转化成二元模型,两相性质与比例是决定混凝土性能的根本因素.
本文在第3种方法的基础上,将混凝土视为粗骨料分散在砂浆中,通过模型化划分,研究了砂浆流变性及用量对其流动性的影响规律,并深入探讨基于分散模型的混凝土流动机理.
1 试验
1.1 试验材料
水泥:P·Ⅱ52.5硅酸盐水泥;减水剂:萘系高效减水剂,粉剂;细骨料:普通中砂,细度模数2.8;粗骨料:5.0~31.5mm 碎石.
1.2 试验方案
定义砂浆中水泥浆体与细骨料的体积比为φP/F,通过改变φP/F(0.78~1.11),配制了8种流变性砂浆,部分砂浆配合比见表1;定义混凝土中砂浆与粗骨料的体积比为φM/C,利用8种流变性砂浆,通过逐步调整φM/C配制了8个系列共40组混凝土试样.表2为部分混凝土配合比.
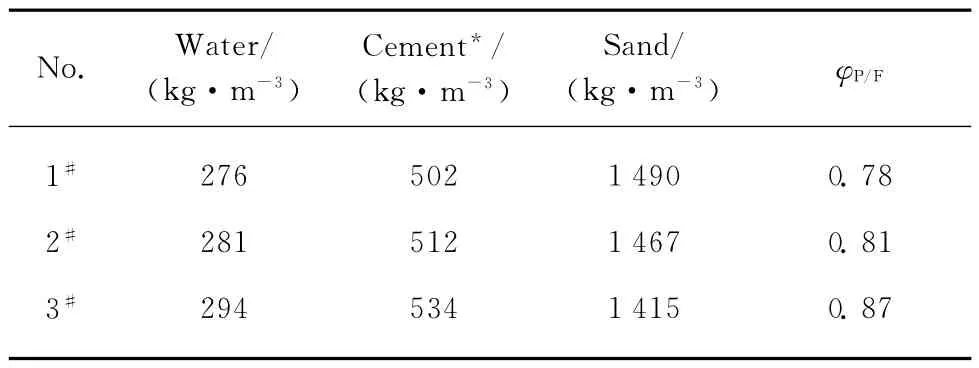
表1 部分砂浆配合比Table 1 Mix proportion of part mortars
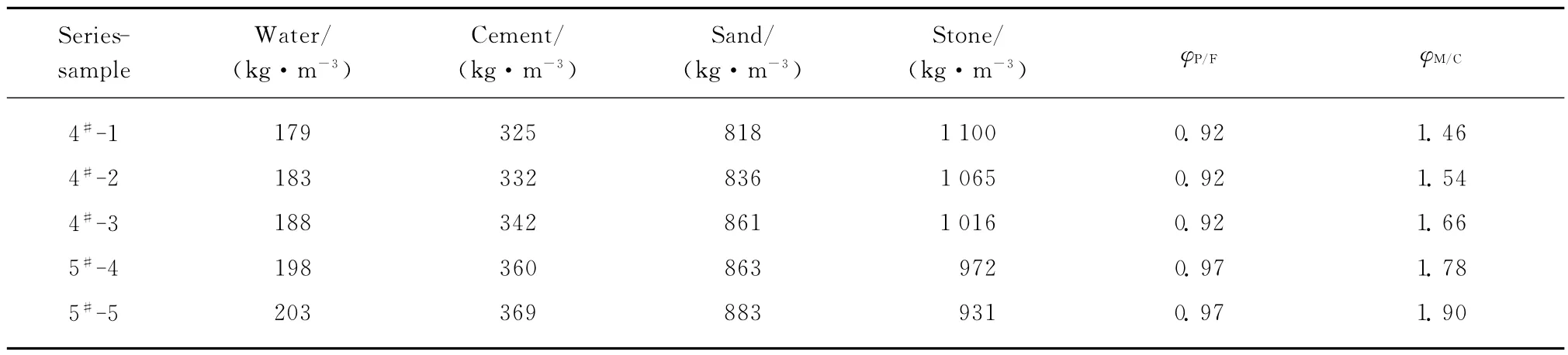
表2 部分混凝土配合比Table 2 Mix proportion of part concrete
1.3 性能检测
参照GB/T 2419—2005《水泥胶砂流动度测定方法》,采用相同的流动度试模,在不施加振动的条件下进行砂浆流动度测试.采用NXS-11B型旋转黏度计测定砂浆的流变参数.
2 结果分析与讨论
2.1 砂浆流变性能的聚类分析
图1为φP/F对砂浆流动度的影响规律.由图1可见,开始时砂浆流动度随φP/F的增加大幅度提高,而后相对平稳.当浆体用量继续增加,砂浆离析,流动度出现波动.砂浆流变性能随φP/F的变化趋势见图2.由图2可见,在φP/F小于0.81时,砂浆屈服应力较高,大于22Pa;当φP/F大于0.87时,砂浆屈服应力显著下降;当φP/F大于0.97时,砂浆屈服应力相对稳定.在φP/F小于0.97的情况下,砂浆的塑性黏度由较高值下降到一个相对稳定值.但是,当φP/F大于0.97时,塑性黏度又会显著提高.在砂浆出现离析之前,砂浆流动度与流变参数的变化趋势一致;当砂浆出现离析时,其塑性黏度急剧增加,同时,砂浆的流动度也出现波动.

图1 浆体用量对砂浆流动度的影响Fig.1 Effect of paste amount on the flowability of mortar
根据流变参数的变化,塑性黏度以0.5Pa·s为分界线,屈服应力以22Pa为分界线,可将上述砂浆分为3类:Ⅰ区砂浆(φP/F为0.78,0.81)为典型的双高(高塑性黏度、高屈服应力)砂浆,这类砂浆由于浆体含量低、润滑作用小,其变形能力较差;Ⅱ区砂浆(φP/F为0.87~0.97)为低塑性黏度、低屈服应力砂浆,其塑性黏度、屈服应力均处于一个相对稳定且偏低的区间,变形能力较强,当φP/F继续增大时,会出现泌水离析,导致黏度较大;Ⅲ区砂浆(φP/F 为1.01~1.11)为高塑性黏度、低屈服应力砂浆.本文通过对砂浆的聚类分析,重点研究了不同类型砂浆对混凝土性能的影响规律.
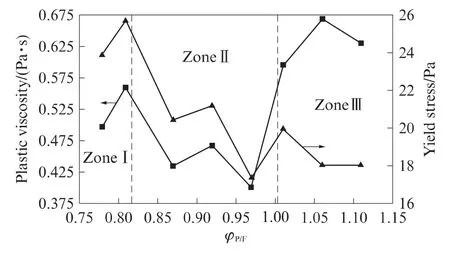
图2 浆体用量对砂浆流变参数的影响Fig.2 Effect of paste amount on the rheology parameters of mortar
2.2 砂浆的润滑与空间分离作用对混凝土流动性的影响
由Ⅰ区砂浆配制的混凝土坍落度随砂浆用量的变化规律如图3所示.由图3可见,随着砂浆用量增加,混凝土的坍落度逐渐增加,且φP/F不同的两种砂浆有着相同的变化规律.由于Ⅰ区砂浆变形能力差、润滑作用小,作为粗骨料相互作用的过渡区,如果增加其厚度,可提高这类混凝土的流动度.

图3 高塑性黏度高屈服应力砂浆混凝土的流动度变化曲线Fig.3 Flowability change of concrete produced by mortar with high plastic viscosity and yield stress
由Ⅱ区砂浆配制的混凝土坍落度随砂浆用量的变化规律如图4所示.由图4可见,随着砂浆用量提高,混凝土坍落度逐渐增大,但增幅并不显著.3个系列混凝土的变化曲线也较为接近,当φM/C由1.40增加到2.00时,混凝土坍落度增加约20mm.提高该类砂浆用量对于混凝土整体流动性影响不大.这说明在此类砂浆作用下,润滑效果对体系的失稳作用比空间分离效果更为显著.
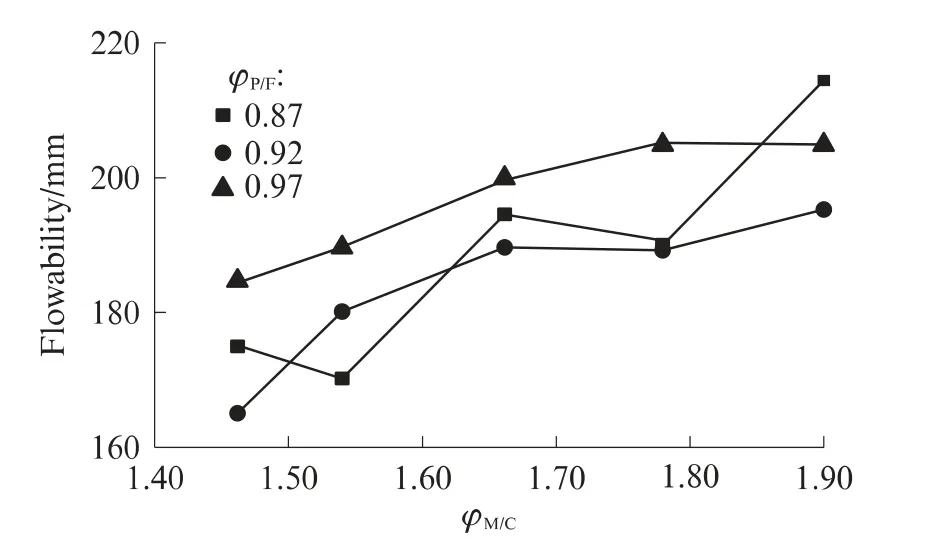
图4 低塑性黏度低屈服应力砂浆混凝土的流动度变化曲线Fig.4 Flowability change of concrete produced by mortar with low plastic viscosity and yield stress
由Ⅲ区砂浆配制的混凝土坍落度随砂浆用量的变化规律如图5所示.由图5可见,随着砂浆用量提高,坍落度逐渐增大,达到极值后逐渐下降至平缓状态.这类砂浆由于存在自由水,可充分润湿粗骨料,从而提高混凝土的流动度.因此,提高砂浆用量可起到润滑和空间分离的双重作用.
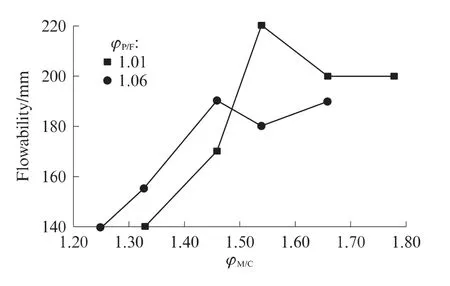
图5 高塑性黏度低屈服应力砂浆混凝土的流动度变化曲线Fig.5 Flowability change of concrete produced by mortar with high plastic viscosity and low yield stress
2.3 混凝土体系失稳因素的相互影响
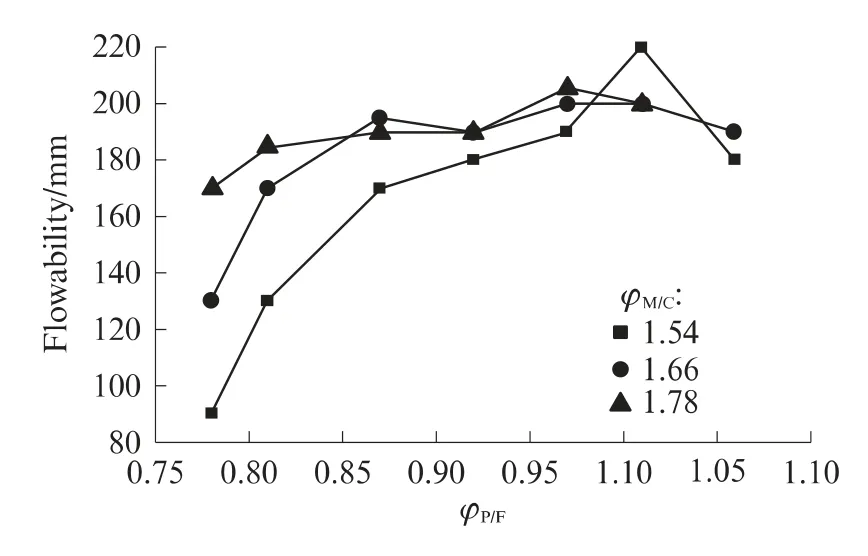
图6 砂浆组成对混凝土流动度的影响Fig.6 Effect of mortar proportion on the flowability of concrete
砂浆流变影响的润滑作用和砂浆用量影响的粗骨料分离作用决定了混凝土的流动性.图6为不同砂浆组成对混凝土流动度的影响.由图6可见,当砂浆用量为粗骨料体 积的1.54 倍时,随着φP/F 的增加,砂浆的变形能力及润滑性能不断提高,导致混凝土的流动度逐渐增大.当φM/C为1.66时,随着砂浆中浆体用量的提高,混凝土的流动度先逐渐增加,之后趋于平稳;当φM/C为1.78时,φP/F产生效果的极限值为0.81,超过0.81,混凝土的流动度提高幅度不大;当φM/C 为1.66 时,φP/F产生效果的极限值为0.87;当φM/C为1.54时,混凝土的流动度随φP/F增加而逐渐提高,且φP/F产生效果的极限值未在本试验检测范围之内.这说明,随着砂浆用量的提高,其润滑作用产生效果的极限值逐渐降低.即当砂浆用量足够大时,砂浆的流动性对混凝土流动性影响不大.
试验表明,砂浆的润滑作用受其流变学参数限制,当砂浆的塑性黏度、屈服应力分别大于0.5Pa·s和22Pa时,砂浆用量提高对混凝土流动性无显著影响;当砂浆体积大于粗骨料体积1.8倍时,其润滑作用不大.
2.4 分散模型对配合比设计的意义
本文利用分散模型来研究混凝土的流动性.在分散模型中,提高浆体用量会同时提高砂浆的流动性和砂浆的用量,导致混凝土坍落度增加,因此,提高砂率具有降低砂浆流动性和增加砂浆用量的双重效果.图7为混凝土坍落度等高图,其中3条连续曲线分别表示浆体体积为0.27,0.29,0.31m3的混凝土,沿曲线由下而上表示砂率逐渐提高.当浆体体积为0.27m3时,随着砂率的提高,混凝土坍落度沿曲线向左上方移动,与不同流动度的等高线依次相交,混凝土坍落度逐渐降低;当浆体体积为0.29m3时,随着砂率的提高,混凝土坍落度逐渐增加;当浆体体积为0.31m3时,混凝土坍落度无显著变化.这说明,砂率的变化同时影响砂浆的流变和用量,而这2个参数的变化趋势正好相反.
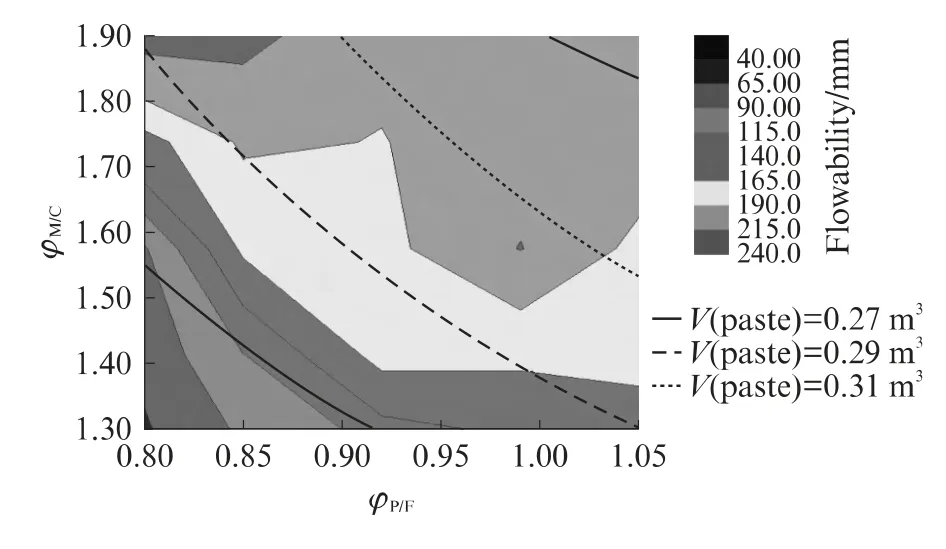
图7 混凝土坍落度等高图Fig.7 Contour map of concrete slump
由图7可见,提高减水率,混凝土坍落度等高线有向上移动的趋势.这是因为固定φP/F后,掺加引气剂一方面可提高砂浆的流动度,另一方面可增加砂浆的体积.砂浆性能的改变方式很多,本文仅采用改变φP/F来调控砂浆性能.
综上可见,改变砂浆用量与砂浆流变这2个参数,可有效调控混凝土性能.
3 结论
(1)随着φP/F的变化,基于流变性可对砂浆进行聚类划分.塑性黏度以0.5Pa·s为分界线,屈服应力以22Pa为分界线,可以将砂浆分为3类,不同类型的砂浆对混凝土流动性的影响规律不同.
(2)基于砂浆流变的粗骨料润湿和依赖于砂浆用量的粗骨料空间分离是造成混凝土体系失稳进而流动的主要因素,并且这两个因素相互影响,当一个因素超过临界值时,另一因素的作用效果被削弱.砂浆的润滑作用受其流变学参数限制,当砂浆塑性黏度、屈服应力分别大于0.5Pa·s和22Pa时,砂浆用量提高对混凝土流动性无显著影响;当砂浆体积大于粗骨料体积1.8倍时,砂浆的润滑作用不大.
(3)利用分散模型能够简便、深入研究混凝土的流动机理.同时,将现有混凝土调控参数分解、转化成砂浆流变和用量2个参数,可为混凝土性能预测及调控提供新思路.
[1]BANFILL P F G.Rheological methods for assessing the flow properties of mortar and related materials[J].Construction and Building Materials,1994,8(1):43-50.
[2]PETIT J Y,WIRQUIN E,VANHOVE Y,et al.Yield stress and viscosity equations for mortars and self-consolidating concrete[J].Cement and Concrete Research,2007,37(5):655-670.
[3]KWAN A,LI L G,FUNG W.Wet packing of blended fine and coarse aggregate[J].Materials and Structures,2012,45(6):817-828.
[4]WONG H,KWAN A.Packing density of cementitious materials:Measurement and modelling[J].Magazine of Concrete Research,2008,60(3):165-175.
[5]LACHEMI M,HOSSAIN K,PATEL R,et al.Influence of paste/mortar rheology on the flow characteristics of high-volume fly ash self-consolidating concrete[J].Magazine of Concrete Research,2007,59(7):517-528.
[6]NOOR M A,UOMOTO T.Rheology of high flowing mortar and concrete[J].Materials and Structures,2004,37(8):513-521.
[7]ERDEM T K,KHAYAT K H,YAHIA A.Correlating rheology of self-consolidating concrete to corresponding concreteequivalent mortar[J].ACI Materials Journal,2009,106(2):154-160.
[8]SAFIUDDIN M,WEST J S,SOUDKI K A.Flowing ability of self-consolidating concrete and its binder paste and mortar components incorporating rice husk ash[J].Canadian Journal of Civil Engineering,2010,37(3):401-412.
[9]DOMONE P.Mortar tests for self-consolidating concrete[J].Concrete International,2006,28(4):39-45.
[10]NG I,NG P L,KWAN A.Rheology of mortar and its influences on performance of self-consolidating concrete[J].Key Engineering Material,2009,400:421-426.
[11]GEIKER M R,BRANDL M,THRANE L N,et al.On the effect of coarse aggregate fraction and shape on the rheological properties of self-compacting concrete[J].Cement Concrete and Aggregate,2002,24(1):3-6.

