2MW风机叶片梁帽与腹板的强度优化设计*

冯消冰，孙树立

（北京大学工学院，北京 100871）

在60年代，Holland 在做了关于自然进化现象和生物的遗传在与人工自适应系统有何相似关系的研究之后，提出了一个全新的概念，就是利用群体进化来模拟适应性系统。而“遗传算法”一词，是在1967年由Holland 的学生Bagley 在他的博士论文[1]中首次提到，并发展了一系列的遗传算子[2]：复制、交叉、变异、倒位、显性等。遗传算法的基本理论-模式定理(Schema Theorem)是在70年代初由Holland 提出来的，遗传算法的理论基础主要由其来奠定。《Adaptation in Natural and Artificial Systems》是第一本系统论述遗传算法和人工自适应系统的专著，它于1975年由Holland 出版。《遗传自适应系统的行为分析》[3]也是于1975年发表， 在De Jong 的这篇博士论文中，进行了很多的纯数值函数优化实验，同时结合模式定理，构建了遗传算法的工作框架，用几个测试函数搭建了著名的五函数测试平台，定义了在线指标和离线指标[4]，用来评价遗传算法的性能。第一本遗传算法教科书《Genetic Algorithm in search，Optimization and Machine Learning》[5]于1989年由Goldberg 出版，该书奠定了现代遗传算法的科学基础。《Handbook of Genetic Algorithms》[6]于1991年由Davis 出版，该书主要阐述了大量应用实例，主要是在工程技术和社会经济这两方面的。Genetic Programming 的概念[7-8]在1992年由Koza 提出，他可以使计算机程序的优化设计及自动生成通过遗传算法来实现。到目前为止，遗传算法还在不断地提高自身的性能，它的发展并没有结束，许多研究者对它表现出很浓厚的兴趣，也在不断地促进它的发展，扬其长避其短，使遗传算法可以更好地发挥其本身的优越性。

在国内的工程领域中，越来越重视遗传算法的优化技术。求解带有离散设计变量或者混台离散设计变量的优化问题尤其适合使用遗传算法，其中的一个比较典型的应用就是复合材料铺层优化设计。许玉荣[9]研究了相对厚度对优化结果的影响，系统的可靠度指标最大为目标，把复合材料层压板结构的重量设置为一定，优化设计了纤维的铺设角。鲁大伟[10]进行层压板设计时采用了免疫遗传算法，由于免疫遗传算法中有对抗体的抑制和促进的机制，这样可以保证种群众个体的多样性，基于给定的层压板面内弯曲因子与几何因子，求解最优的铺层顺序，最终以较高的收敛效率得到了待求解问题的最优解。徐超[11]提出了免疫算法其实具有更高的收敛效率，并将层压结构的优化设计问题使用免疫算法来求解，计算得到了复合材料层压板铺层顺序的优化结果，也认为优化结果受免疫算法记忆抗体群大小控制参数的影响，记忆抗体群值越大，导致运算量也越大，从而收敛精度越高。晏飞[12]得到了较高的收敛速度相比于标准的遗传算法，因其研究复合材料层压板的铺层顺序优化设计问题时，采用的是多级优化技术和自适应遗传算法，这样能够通过适应度的大小，自适应地选取突变概率和杂交概率。任茶仙[13]也用遗传算法进行了层压板的铺层顺序优化，给出了一种新方法，用于求解结构组合优化问题，此方法基于生物免疫系统抗体浓度调节原理，采用抗体选择概率算子与抗体浓度成指数递减，与抗体的适应度成正比，同时也考虑到抗体调节系数随着搜索的进行，而动态变化，这样可以有效地把高适应度的抗体保留，又可以确保种群的多样性，最主要的是可以保证得到的是全局最优解。唐文艳[14]采用整数编码的方式，并对遗传算法做了一些改进，还对解码的过程进行了特别的处理，使得个体满足了对称均衡铺层要求，也是采用遗传算法求解了层压板铺层顺序优化的问题，把临界屈曲载荷系数或固有振动频率极大化作为优化的目标，较有效率地搜索到最优解。李磊[15]合理设置了遗传算法的运行参数，使得“早熟”现象避免发生，同时使单次计算中，可以得到全局最优解的概率高至0.95 以上，最终实现了使用遗传算法对含弹性支撑与集中质量的层压板固有频率的最大化问题进行了优化。王共冬[16]考虑的优化模型的约束条件为相关的铺层知识，考虑到铺层结果受铺层的一些启发式知识的约束，对层压板铺层进行了优化时使用了自适用遗传算法，优化的过程之中，选中知识规则的校验应用于每次迭代之中，这样可以加快收敛速度。王向阳[17]的优化目标为最终失效强度，设计变量为层压板厚度与纤维方向角度，来进行复合材料结构的优化。

本文在实现强度优化设计之中，也应用了遗传算法，引入强度比的概念来进行复合材料结构的强度优化，同时也构建了合适的适应度函数。考虑到复合材料结构的离散型优化特点，层压结构参数用整数型编码方式来表征。最后实现了使用遗传算法对2MW 大型风机叶片的梁帽和腹板进行强度优化设计。

1 复合材料层压结构弹性特性

1.1 单层应力-应变关系

正交各向异性材料，平面应力状态下单层复合材料在材料方向上的应力应变关系为：

将(1)写成应力-应变关系式：

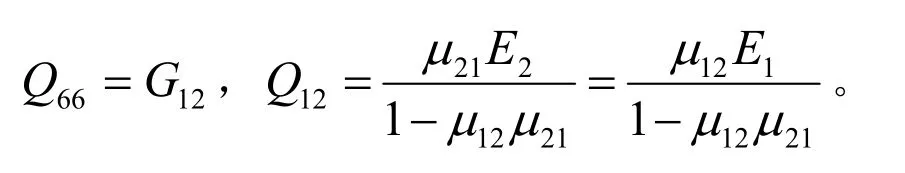
Qij是二维刚度矩阵， E1、 E2、 G12、 μ12、 μ21分别为正交各向异性材料的面内工程弹性常数。 复合材料结构设计和分析所取的整体坐标系往往不完全与材料的正轴坐标系重合。为了能在统一的x-y 坐标系下计算材料的刚度，需要知道单层材料在非主方向，即图1 中x、y 方向上的弹性系数(称为偏轴的弹性系数)与材料主方向的弹性系数之间的关系，θ表示从x 轴转向l 轴的角度，以逆时针转为正。

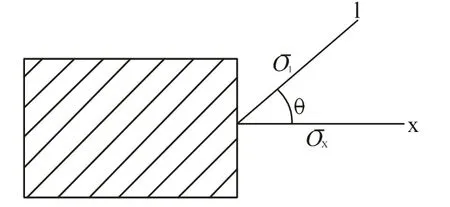
图1 单层复合材料偏轴方向的应力表示 Fig.1 The stress of monolayer composite in direction apart from the axis

记转换矩阵[T]为：

则偏轴方向上的应力和应变与正轴方向间的关系分别为：

则偏轴方向上的应力-应变关系为：

将式(6)改写成

记转换后的折算刚度矩阵为：

1.2 层压板的应力-应变关系

层压板任意层的应力可以通过应变计算如下：

1.3 层压板的内力-应变关系

复合材料经典层压板内力与应变的本构方程为：

式中

2 复合材料的蔡-吴(Tsai-Wu)强度准则

蔡-希尔准则考虑了材料的正交异性，并照顾到纤维增强复合材料的某些特点，但是大量的实验结果表明，纤维增强复合材料在材料主方向上的拉压强度并不相等，某些复合材料的横向拉压强度竟相差几倍之多，用蔡-希尔准则来判定会有很大的误差。因此蔡和吴(E.M.Wu)在综合了许多准则的基础上，于1971年提出了蔡-吴（Tsai-Wu）准则：

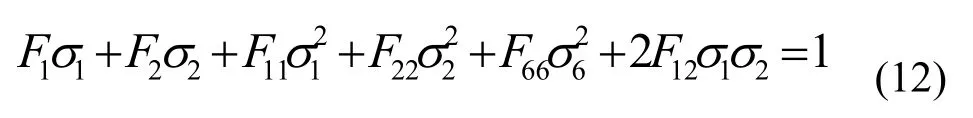
对于实际的应力状态，(12)式左端各项之和正好等于1，表示材料处于开始破坏的临界状态；若小于1，表示材料处于安全状态；若大于1，表示材料已经破坏。

3 复合材料结构强度优化设计的遗传算法实现

3.1 编码

遗传算法常采用有限长度的二进制串来表示所求问题的解。对离散变量问题，二进制编码串的长度与变量的可选离散值有关.当离散值个数与二进制所能表示的离散值个数不能一一对应时，往往是从离散值列表中选值进行补充，这样某些离散值就有不同的二进制编码表示。但是整数编码表示解决了这个问题，编码的长度就是设计变量的个数，变量离散值和编码表示能够一一对应，而且节省了二进制向整数的转换过程。故采取整数编码方式。用整数{0，1，2，3，…}来代表铺层的角度。层压结构设计采用的铺层角度多为：{0°，-45°，45°，90°}，则分别用0、1、2、3 来表示0°铺层角、-45°铺层角、45°铺层角、90°铺层角。采用这种整数编码方式的主要优点是：(1)符合有意义基因块编码原则[18]；(2)比较直观反映了层压结构通过调整铺层顺序进行优化设计的特点，便于在遗传算法中利用所求解问题的专门知识。

3.2 适应度函数

所选的优化目标选为层压板的强度，这里引进强度比的概念。所谓强度比就是，在作用应力下，极限应力某个分量与其对应的作用应力分量的比值称为强度/应力比，简称强度比，记为R，即：

式中，)(aiσ 并不仅仅是材料的单向载荷许用应力值，它可以是复杂应力状态下的许多分量， iσ 表示工作载荷在层压壳结构件上引起的工作应力分量。 将许用应力代入蔡-吴准则方程中，有：

这是一个关于R 的二次方程，称为强度比方程。

强度比R 是安全系数的一种度量，R 的具体数值表明，作用应力或者应变达到失效时，尚可以增加应力或应变的倍数为R-1。

遗传算法进行计算时使用的适应度函数表示如下：

其中，n 为层压板总层数，R(i)为每一单层的强度比。由此可见，遗传算法进行层压板最大强度的优化过程就是寻找群体中最小单层强度比的最大值的过程。

4 叶片梁帽铺层优化设计

叶片主要由上、下壳体和前、后腹板构成，前、后腹板开口相对与壳体构成矩形盒式结构。腹板内填充泡沫夹芯。壳体前缘、后缘部分，填充泡沫夹芯以减轻叶片重量，增加结构刚度。叶片的典型切面示意图见图2。

图2 叶片典型切面结构示意图 Fig.2 The sketch scheme of typical profile structure

4.1 叶片梁帽载荷计算

表1 是将叶片的梁帽起始位置处所受各种载荷分别组合在表中，同时找出每种计算工况的最大值与最小值。这些载荷是在GL 坐标系中计算得到的、以公制单位的形式给出(运用了安全系数)。

表1 叶片极限载荷 Table1 The ultimate load of blades

4.2 叶片梁帽铺层优化

材料为高模量E 玻璃纤维/环氧树脂，铺层角度在0°、-45°、45°、90°之间选择，层数选为35层。层压结构为一般斜交层压结构，由不同方向并以非规则顺序的正交单层组成(非均衡、非对称)，所计算的所有刚度系数均非零，存在拉弯耦合效应和层间应力，同时考虑相关的铺层规则。选择各单向层为等厚度，厚度t=0.87038mm。应用遗传算法中，种群规模选为80，进化代数为100，竞赛规模为70，交叉概率为0.85，变异概率为0.05。

考虑到叶片梁帽的受力情况应为在GL 坐标中的Nz 为最大，故选取1.6t 工况进行计算，经坐标转换之后，在 1.6t 工况中取 Nx=476032N/m，Ny=25318N/m，Nxy=0，Mx= -975N，My= -6388N，Nxy=0。遗传算法求解的结果如表2。

表2 1.6t 工况的叶片梁帽铺层优化 Table 2 The optimization of layer in blade cap of load case in 1.6t

4.3 叶片梁帽铺层优化方案与原方案的比较

叶片梁帽原铺层方案为35 层，全部为0°铺层。具体的铺层顺序如表3。

表3 叶片梁帽原铺层方案 Table 3 The original laminate project of blade cap

因原铺层方案仅考虑叶片在展向方向的受力，并未考虑弦向方向的力及所受的弯矩，也未考虑相关的铺层规则，故铺层设计较为简单，强度比也较低，安全余量不足。在经过遗传算法优化铺层之后，叶片梁帽铺层的强度比有了较大的提高，原铺层方案与优化铺层方案的比较见表4。

表4 叶片梁帽铺层优化方案与原铺层方案的比较 Table 4 The compare of layer in blade camp between original project and optimized project

5 叶片腹板铺层优化设计

5.1 叶片腹板铺层优化

材料为高模量E 玻璃纤维/环氧树脂，铺层角度在0°、-45°、45°、90°之间选择，层数选为8 层。选择各单向层为等厚度，厚度t=0.61018mm。应用遗传算法中，种群规模选为80，进化代数为50，竞赛规模为70，交叉概率为0.85，变异概率为0.05。

叶片腹板的主要作用是抗剪，故选择叶片腹板起始位置处的极限工况1.3b，因此位置处的弯矩主要由叶片蒙皮及叶片梁帽来承担，故计算值选取中忽略了弯矩作用，取Nx=116347N/m，Ny=67586N/m，Nxy=0，Mx=0N，My=0N，Mxy=0。遗传算法求解的结果如表5。

表5 1.3b 工况的叶片腹板铺层优化 Table 5 The optimization of layer in blade shear web of load case in 1.3b

5.2 叶片腹板铺层优化方案与原方案的比较

叶片腹板原铺层方案共为8 层，全部为-45°与45°铺层。具体的铺层顺序如表6。

表6 叶片腹板原铺层方案 Table 6 The original laminate project of blade shear web

在经过遗传算法优化铺层之后，叶片腹板铺层的强度比略有提高，原铺层方案与优化铺层方案的比较见表7。

表7 叶片腹板铺层优化方案与原铺层方案的比较 Table 7 The compare of layer in blade shear web between original project and optimized project

以上叶片梁帽及叶片腹板的优化铺层全部是根据起始位置处的极限工况进行计算，在后续工作之中，应根据各截面的计算载荷，沿着叶片展向方向对各截面的铺层层数进行删减，具体计算过程就不在此一一列出了。

叶片蒙皮的结构形式为封闭型的薄壳三明治结构，铺层设计时除了应考虑强度比外，还应主要考虑叶片蒙皮的屈曲问题。

6 结论

本文在所计算叶片载荷的基础之上，应用遗传算法在强度优化设计中的计算方法，针对叶片梁帽铺层及叶片腹板铺层，进行了铺层的强度优化设计，得到了较好铺层优化结果。

(1)在经过遗传算法优化铺层之后，叶片梁帽铺层的强度比有了较大的提高，从原铺层方案的1.1523 提高到了优化铺层方案的3.2244。

(2)在经过遗传算法优化铺层之后，叶片腹板铺层的强度比也有所提高，从原铺层方案的3.5079 提高到了优化铺层方案的3.7657。

(3)铺层只在0°、-45°、45°、90°这四种角度之间选择，故存在较大的局限性。如可以在任意角度下铺层，则得到的优化后的强度比会更大，表明层压板的设计性具有很大的潜力。

[1]Bagley J D. The behavior of adaptive systems which employ genetic and correlation algorithms[D]. University of Michigan, 1967.

[2]陈永兵. 遗传算法及其在结构工程优化中的应用研究[D]. 西北工业大学，2000.

[3]De Jong K A. An analysis of the behavior of a class of genetic adaptive systems[D]. University of Michigan，1975.

[4]周敏. 遗传算法的若干改进及应用[D]. 中国科学院，2001.

[5]Goldberg D E. Genetic algorithms in search，optimization and machine learning[M]. MA: ：Addison-Wesley Publishing Company，1989：37-39.

[6]Davis L D. Handbook of genetic algorithms[M]. New York：Van Nostrand Reinhold，1991:20-23.

[7]Koza J R. Genetic programming 1[M]. Cambridge：MIT Press，1992：65-68.

[8]Koza J R. Genetic programming 2[M]. Cambridge：MIT Press，1994：45-56.

[9]许玉荣，陈建桥，罗成，等. 复合材料层合板基于遗传算法的可靠性优化设计[J]. 机械科学与技术，2004，23(11)：1344-1347.

[10]鲁大伟，李书. 应用免疫遗传算法优化设计层合板铺层顺序[J]. 北京航空航天大学学报，2005，31(2)：247-250.

[11]徐超，聂常胜，张铎. 基于免疫算法的复合材料铺层顺序优化设计[J]. 机械强度，2008，30（3）：376-380.

[12]晏飞，李为吉. 基于自适应遗传算法的复合材料层合板铺层顺序优化设计[J]. 西北工业大学学报，2001，19(1)：156-159.

[13]任茶仙，张铎. 复合材料层合结构铺层顺序优化设计的免疫遗传算法[J]. 强度与环境，2007，34(2)：44-50.

[14]唐文艳，顾元宪，赵国忠.复合材料层合板铺层顺序优化遗传算法[J]. 大连理工大学学报，2004，44(2)：186-189.

[15]李磊，雷勇军，唐国金. 基于遗传算法的含集中质量和弹性支撑复合材料层合板固有频率优化设计[J]. 强度与环境，2008，35(3)：20-26.

[16]王共冬，等. 基于启发式知识的自适用遗传算法的复合材料铺层优化设计[J]. 玻璃钢/复合材料，2009(2)：3-5.

[17]王向阳，郭奔. 基于最终失效强度的层合板结构优化分析[J]. 武汉理工大学学报(交通科学与工程版)，2006，30(1)：140-143.

[18]Sun C T，LI Si jan. Three-dimensional effective elastic constants for thick laminates[J]. Composite Materials，1984，22.