偏微分方程解的数值验算
蔡姝婷
(福建江夏学院 数理教研部,福建 福州 350108)
偏微分方程解的数值验算
蔡姝婷
(福建江夏学院 数理教研部,福建 福州 350108)
本文提出一种偏微分方程解的数值验算方法.首先应用有限元的方法求偏微分方程的数值解,然后将偏微分方程的解转化为一个紧算子的不动点,我们验证算子在某一个集合中满足不动点定理,从而偏微分方程的解存在.接着通过分析的方法将不动点定理的条件转化为计算机可以计算的条件,最后结合区间验算的方法避免计算机计算过程中存在的截断误差,从而证明所求近似解的附近存在精确解.
偏微分方程;数值验算;不动点定理;区间验算
1 引言
偏微分方程在自然科学和技术科学领域中都具有很广泛的应用.在每年的各类型数学建模竞赛中,运用偏微分方程进行建模是一种常见的建模方法.如反应扩散型方程中的食饵-捕食者模型,可以模拟两个不同的种族间的相互作用,其中一个种族捕食另一个种族;Schnakenberg模型描述发育生物学中的一些模式形成等等.如何求这些偏微分方程的解是能否完成一个数学建模过程的重要的问题.到目前为止,能够运用解析的方法求解的偏微分方程类型相对有限.但是,随着计算机计算能力的增强以及数值计算方法的发展,偏微分方程的数值解法越来越多,通常运用一些有限元的方法将偏微分方程离散化后进行求解,之后需要求出相应的误差.有部分的数学软件如Matlab可以用自带的软件包直接进行数值计算,但这样的数值计算过程都带有一定的误差,无法严格地证明方程的解确实在某个范围内是存在的.本文的方法是对传统的数值计算方法的发展,提出通过数值验算的方法验算偏微分方程解的存在性.我们先用有限元的方法求出偏微分方程的数值解,然后将偏微分方程的解转化为一个方程的不动点,根据不动点定理,验证在一个小区域内,这个方程的不动点存在.这个验证的过程是通过计算机来完成的,而计算机在内部计算的过程中,存在一定的截断误差,我们应用区间演算[1]的方法来避免这个误差.整个计算过程我们将在Matlab上实现.通过我们的方法,一方面可以得出方程解的大致形态,另一方面,也可以用计算机进行严格的证明解确实是存在的以及解所存在的小范围.
我们选取较为简单的偏微分方程说明本文的方法.考虑具有Dirichlet边界条件的偏微分方程

其中Ω=(0,1)×(0,1),f(x,y)是关于x,y的函数,d是一个常数.
方程(1)近似解的求法有很多种,在[2]中介绍了多种求解偏微分方程数值解的有限元方法.本文同样将应用有限元的方法求解方程(1),只是对于基函数的选取有所不同.
首先,对于任意的整数m,我们定义Hm=Hm(Ω)为m阶的L2-Sobolev空间.同时我们定义H01:=H01(Ω):={u∈H1|u=0 on Ω},并具有内积〈ø,ψ〉=(▽ø,▽ψ),其中(·,·)表示L2(Ω)空间上的内积.我们考虑方程(1)在H01空间中解的存在性.
我们选取基函数φi1i2为

对于一个固定的非负整数N,我们按以下规则对基函数重新排序,

从而基函数成为

假设H01中的所有元素ψ可展开为傅利叶级数

选取适当的N,我们在有限维空间

2 近似解
在这一节中,我们将在空间SN中计算方程(1)的近似解.对任意的vN∈SN令

因此我们现在的问题是,求uh∈Sh,使得

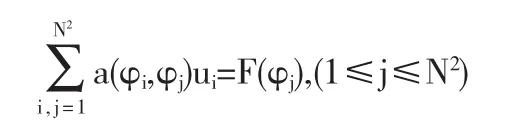
将上述问题写成矩阵形式,即

其中

我们运用Matlab即可求出方程(1)的数值解.
3 解的数值验算
我们知道对于任意的ψ∈L2(Ω)下列的泊松方程存在一个唯一的根ø∈H1∩H'0:

将方程(2)的解记为ø=L-1ψ则L-1:L2→H01是一个紧算子.
令K(u):=L-1(f(x,y)+du),那么K是H01上的紧算子,并且方程(1)的解为算子K的不动点:

因此由Schauder不动点定理,如果我们能在H01中找到一个非空的,有界的,凸的闭集合满足

那么在K(U)中就存在一个元素u使得u=Ku.我们的做法是在计算机中构造一个侯补的集合U=UN⊕U⊥,其中UN⊂SN,U⊥⊂SN⊥.这里SN⊥表示SN在H01空间中的正交补空间.这样,我们可以将验证条件(4)转化为

Moore在[1]中介绍了区间演算的方法.由于在计算机计算的过程中存在截断误差,比如在数学软件Matlab中,以双精度符点型数据进行计算,当我们计算1/3时,计算机内部以64位小数进行计算,截断了小数点后的值,由此产生了误差.我们应用区间演算来避免这种误差,如同样计算1/3时,计算机内部以[0.33333333333333,0.33333333333334]计算.此时既有1/3落于这个小区间内,避免了截断误差,同时这个区间的范围较小,满足一定的精度要求.为了计算的顺利进行,我们定义了区间演算的加减乘除法.对于实数集上的任意两个区间,X=[a,b],Y=[c,d],我们定义下列运算:

其中x=min{ac,ad,bc,bd},y=max{ac,ad,bc,bd}.同时还定义

例如:[1,2]·[-2,1]+[0,1]=[-4,3].另外,区间X的幅度定义为:d(X)≡b-a.绝对值为:|X|≡max{|a|,|b|}以及中点为m(X)≡(a+b)/2.Rump根据这些运算规则,在[3]中建立了一个基于区间演算的区间实验室,实现了在计算机上完成区间演算的过程.
我们这里将用这种区间演算的方法验证条件(4)的成立.对于条件(4)的有限维部分PNK(U)⊂UN的验证,我们把候补集合UN定义为


其中Bi是由方程

所确定的.
而对于无限维部分的验证,我们需要一个引理:
引理1 对任何的ø∈H2∩H01,存在一个正常数CN,使得


定理1如果

成立,那么在U中存在一个方程K(u)=u的解.
根据这个定理,我们可以得到验证解存在性的一个算法:
算法1


4 数值结果
我们选取具体的d及f进行计算.若d=1,f(x,y)=x+y.取N=20.我们用Matlab软件得到方程(1)的近似解如图1所示.接着利用区间演算实验室[3]以及算法1进行数值验算,得到区间长度的最大值为0.004,β0=0.0175.本文所得到的计算结果是在HP ENVY 6 Notebook PC [Intel(R)Core(TM)i5-3317U@1.70 GHz]电脑上用Matlab (Ver.7.0)完成的.

图1
注:本文的方法针对于相对较为简单的方程(1)进行求解,具有一定的局限性.如果所遇到的方程关于u是非线性的,同样是可以用数值验算的方法进行求解.在求近似解时,可以先用Newton法,而后的数值验算过程可以采用一种近似的牛顿法,结合不动点定理加以验证.这是我们今后的研究方向.
〔1〕Moore R.E.Intervalanalysis[M].Englewood Cliffs: Prentice-Hall,1966.
〔2〕马昌凤.有限元方法讲义[Z].2006.
〔2〕Rump S.M.,INTLAB-INTerval LABoratory[Z],a Matlab toolbox for verified computations,Version 5.5.Inst,Informatic,TU Hamburg-Harburg,http://www.ti3.tuharburg.de/rump/intlab/.
O175.2
A
1673-260X(2015)09-0007-03
本文由教育部留学回国人员科研启动基金资助项目资助

