奇异积分算子在BLO空间特殊界性介绍

陈杨洋

（安徽理工大学 地球与环境学院，安徽 淮南 232001）

奇异积分算子在BLO空间特殊界性介绍

陈杨洋

（安徽理工大学 地球与环境学院，安徽 淮南 232001）

BLO空间是随着BMO空间的发展而发展起来的，BLO空间起的作用正如Hp空间在L1空间中所起的作用一样，本文研究BLO空间中的奇异积分算子的有界性质，首先先给出BLO空间的定义，为研究奇异积分算子在BLO中的作用做好准备.其次给出了奇异积分算子在BLO空间特殊有界性.

BLO空间；BMO空间；奇异积分；有界性

对于Rn(n≥2)，定义Ω为该域上的零次齐次函数，由第一章已经知道，奇异积分算子和极大奇异积分算子可以表示如下：

我们可以知道，对于T和T*而言，在Lp(Rn)(1＜p＜∞)区域内有界，并且T*对于所有的f∈Up≥1Lp(Rn)都存在有界性.那么就有

此时，BLO(Rn)⊂BMO(Rn)，即BLO(Rn)是BMO(Rn)的一个子空间.基于此，我们首先将函数空间域局限在BLO(Rn)中.

特殊有界性定理

极大奇异积分算子T*满足上述条件情况下，并且Ω域内为一个可积的单位球，平均积分值为零.对于q＞2，Ω∈L1(∑)q(Sn-1)，那么有

并且在L1上Ω的连续模满足

对于任意f∈BMO(Rn)，T*要么是处处有限的，要么几乎是处处无限的.更细致的讲，如果f∈BMO(Rn)，对于x0∈Rn而言，T*f(x0)＜∞；对于其他的x0，则T*f(x0)是无限的.所以有

并且有对于一个球型的B和γ＞1：

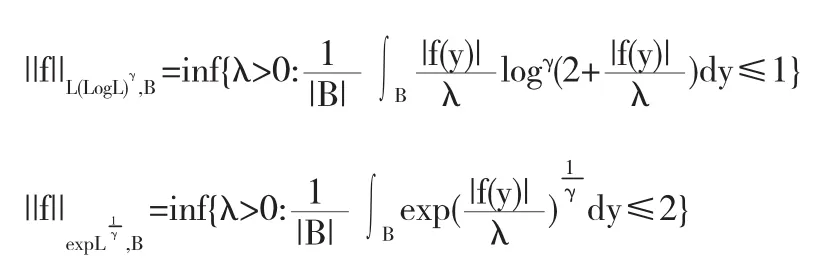
因此我们得到

特殊有界性定理证明

引理1 假设Φ(t)是一个Young函数，ψ(t)是它的互补Young函数，那么就存在一个正常数C使得对于任意0＜t1,t2＜∞，

比如说Φ(t)=tlog(2+t)，ψ(t)=exp(t)，那么对于任何a＞0和0＜t1,t2＜∞，

引理2 对于任意f∈BMO(Rn)并且τ＞0，存在一个正常数C，使得

关于引理2的证明如下：

不失一般性而言，我们可以假设||f||BMO(Rn)=1，对于每一个固定的R≥2τ，记为：

同理，我们可以得到G≤C，I1≤C.从而综合I1，I2，I3可得特殊有界性定理成立.

〔1〕Colin Bennett.Another characterization ofBLO[J].Proceeding of the American Mathematical Society,Volume 85,Number 4,August 1982.

〔2〕G.E.Yan&D.C.Yang,Estmates for Marcinkiewica integrals in BMO and Campanato spaces[J].Glasgow Math J.2007,(49):167-187.

〔3〕E.Stein.Harmonic analysis real-variable method,orthogonality,and oscillatory integrals[M].Princeton Univ Press,1993.

〔4〕张恭庆,林源渠.泛函分析讲义[M].上册.北京:北京大学出版社,1987.

〔5〕程民德,邓东皋,龙瑞麟.实分析[M].高等教育出版社,1993.

〔6〕韩永生.近代调和分析方法及其应用[M].科学出版社,1988.

〔7〕Leckband,M.,Structure resultson maximalHilbert transform and tow-weight inequalities,Hadiana Uviv.Math.J,1985,34:259-275.

O175.5

A

1673-260X（2015）09-0004-03