基于小波分析的MEMS加速度计输出噪声消除

童姣叶，李荣宽，杜 微

（电子科技大学电子工程学院，成都611730）

基于小波分析的MEMS加速度计输出噪声消除

童姣叶，李荣宽*，杜 微

（电子科技大学电子工程学院，成都611730）

目前MEMS加速度计普遍存在信噪比低、灵敏度不高等缺点，其主要原因是系统内部电路中的干扰与噪声使得有用信号完全淹没在噪声之中，其中1/f分形噪声是主要的噪声。由于1/f分形噪声在小波域中展示出某些特殊性质，且小波分析兼具时-频分析与尺度分析的功能，为了有效消除1/f分形噪声，提出了一种基于小波分析与自适应阈值滤波的多尺度滤波算法。以信噪比、均方根误差作为去噪效果的定量指标，将本文算法与Donoho小波阈值滤波算法进行比较，仿真结果表明，改进的自适应阈值滤波算法优于Donoho阈值滤波算法。运用于MEMS加速度计噪声消除上科学有效。

MEMS加速度计；1/f分形噪声；小波分析；自适应阈值滤波

自MEMS技术及IC工艺发展以来，MEMS加速度计以其简单结构、低成本和高精度在应用范围上迅速扩展。由于MEMS传感器非常小，除通常的电子设备中的噪声源之外，检测质量块布朗运动产生的噪声即分形噪声（1/f噪声）也会对加速度计输出信号产生明显的影响，而输出噪声会直接影响到加速度计的输出精度。

1/f噪声是一类具有自相似性、长相关性以及非平稳性的随机噪声。其非平稳性要求进行时间分析，而其自相似性却要求进行尺度分析［1］。小波变换是时空频率的局部化分析，在时域和频域同时具有良好的分辨性，利用多尺度分析方法，可以在不同的尺度下观测信号不同精度的局部特征。由于信号和1/f噪声经过小波变换后的统计特性不同，从而在多尺度分析中呈现出不同的传播行为［2］，且小波分析可以把非平稳过程分解成一系列平稳过程，可以利用这一特性采用小波阈值消噪分别对每一个平稳过程进行消噪［3］。但传统的硬阈值和软阈值消噪都存在一定的缺陷，如硬阈值去噪会因断点而造成局部震荡，软阈值去噪会丢失奇异点信息等［4］。

本文将含1/f噪声的信号进行多尺度正交小波分解，在各尺度上选取不同的阈值对细节系数进行滤波处理，滤除掉包含噪声信息的系数，最后通过逆正交小波变换对滤波后的系数进行重构，从而达到提取有用信号的目的。

1 算法原理

1.1 1/f噪声模型与其性质

本文指的1/f噪声采用Mandelbrot与Van Ness建立的分数布朗运动（FBM）模型，因其在数学处理上的简便性而成为统计自相似信号的一个最经典模型。分数布朗运动BH(t)是一类非平稳、零均值、高斯分布的随机函数。其定义如下［4］：

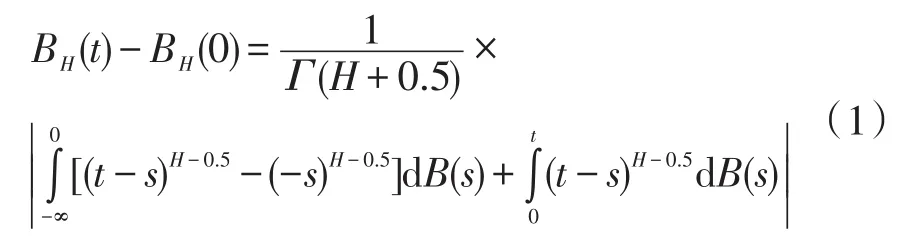
式中：BH(0)=0，H指数称为Hurst指数，代表自相关参数，且0＜H＜1。当H=0.5，分数布朗运动是维纳过程，即为经典的布朗运动。

分数布朗运动的自相关以及增量性质如下：

式中：s,t∈R，

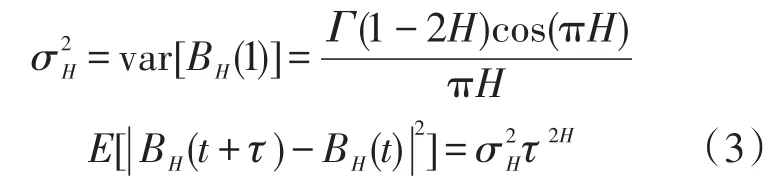
由式（2）可知，分数布朗运动BH(t)是非平稳的随机过程。式（3）是其增量的方差公式，直观地反映了其在时间域的统计自相似性。由于BH(t)是非平稳的随机过程，因此并不具有通常意义上的功率谱，其经验形式的功率谱密度呈幂指数规律变化：

式中g=2H+1，表明分数布朗运动是以谱参数为1＜g＜3的1/f过程。

从统计意义上看，分数布朗运动以H参数自相似。对于任意实数a＞0，存在如下尺度关系：

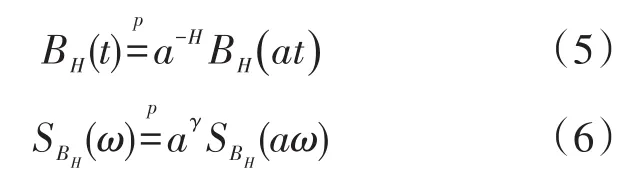
1.2 1/f噪声的小波变换特性

通过1.1节的描述，可以知道分数布朗运动可作为谱指数为1＜g＜3的1/f噪声的模型。由于传统的信号检测理论如相关检测、匹配滤波等都假定背景噪声是平稳的白噪声，同时传统的分析方法大多不能有效去除自相似及长程相关性，要从具有局部自相似及长相关性的1/f噪声中检测出有用信号，在处理上遇到了很大困难。小波变换是傅里叶变换的继承和发展，具有时频局部化、多分辨率和去相关性的特点，很适合处理1/f噪声［4］。Wornell等研究了1/f过程的小波变换特性，发现其小波系数序列的特殊性质，方便了1/f噪声的分析与处理。

Wornell在文献［1］中详细研究了1/f分形信号二进制小波变换系数（j为尺度，K为j尺度上对应点）的特性，并证明当基本小波的消失矩为R，且谱指数满足：0＜g＜2R，则对任意两个不同尺度间的细节系数的归一化相关系数如下［5］：

上述性质使得利用离散小波变换处理1/f噪声变得有效、便捷，它能将1/f噪声时间域上的自相似性变换到小波域的尺度上去，此时小波系数序列的长相关性与自相似性将被大大衰减。若选取高阶消失矩的正交小波函数处理，可以认为其是不相关或者弱相关的，从而可以采用传统的平稳信号处理方法对其小波系数做进一步处理［7］。

2 自适应阈值滤波算法设计

Donoho在文献［8］中提出了软阈值的小波滤波方法从噪声中恢复有用信号，该方法比较简洁且计算量小，能满足通常的消噪需求。假设信号的基本模型为：

其中，ti=i/n,zi是标准的高斯白噪声且σ是噪声水平，阈值为：，γ1阈值常数，软阈值函数定义为：

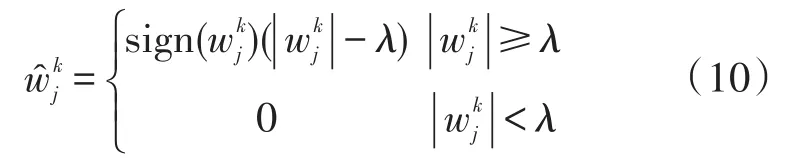
对信号连续做多次小波分解后，由MEMS加速度计的有用输出信号s(ti)所对应的各尺度上小波系数在某些特定的位置有较大值，这些点对应于原始信号s(ti)的奇变位置和重要信息，而其他大部分位置的值较小，对应于信号的缓变部分；白噪声zi所对应的小波系数在每一尺度上的分布是均匀的，并随着尺度的增加而减小［9］。文献［10］指出各尺度下细节分量的自相关系数反映了噪声与信号比重的大小关系，从而证明了噪声分量开始较大，随着分解尺度的增加迅速减小然后趋于稳定，也就是说，在较低分解尺度上，噪声引起的小波系数幅值很大，而在较高分解尺度上很小，这就需要小波阈值在较小分解尺度上取较大值，从而尽可能多地去除噪声，随分解尺度增加阈值迅速减小并趋于稳定，从而保留更多的有用信号。

为此本文在在Donoho提出的软阈值消噪方法的基础上，本文提出了一种改进的方法，即在不同尺度j上自适应选取不同的阈值，将阈值修正为式（11）其中a、b、c为调节因子，b＜0。

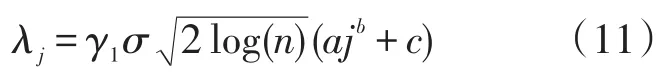
多次实验发现，对于MEMS加速度计的输出噪声而言，当a=1.22，b=-1.16，c=0.29时，去噪效果较好。

基于小波分析的MEMS加速度计消噪按以下三个步骤进行：

①信号分解：选择合适的小波基并确定分解尺度j，对信号进行多尺度正交小波分解，得到各尺度小波系数

②细节系数的阈值量化：按照式（11）选取各尺度阈值λj，采用式（10）的阈值函数对各尺度细节系数进行处理，处理后的细节系数基本可认为是由信号产生的。

由1.2节对1/f噪声的小波特性分析可知，对1/f噪声采用高阶消失矩的小波基进行分解，其细节系数的均值为0，方差为σ2(2j)γ，因此对MEMS加速度计中1/f噪声进行滤波时，应将σ调整为σ=σ2γj/2。考虑到除1/f噪声外，加速度计信号中还有高斯白噪声，此时σ应调整为，其中为高斯白噪声的方差，这样可将1/f噪声和白噪声同时滤除掉［11］。

③信号重构：利用小波逆变换对处理后的系数进行重构，即可得到去噪后的信号。

算法实现框图如图1所示。

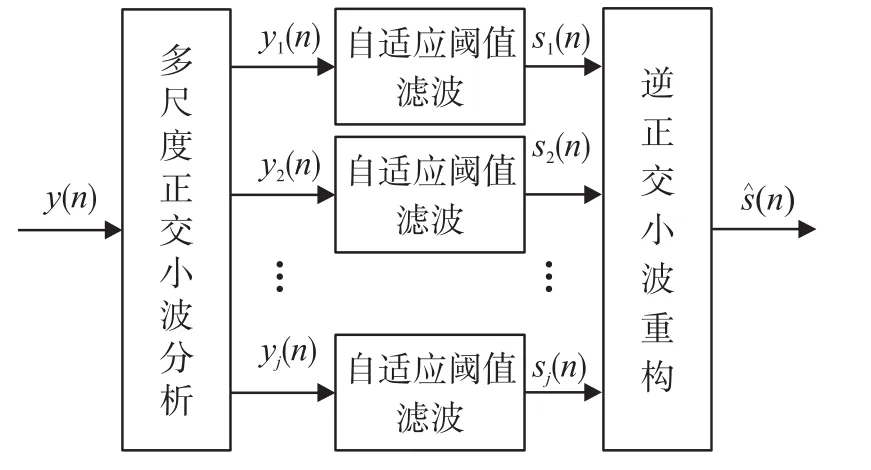
图1 1/f噪声消除算法实现框图

3 仿真实验

为验证上述去噪方案的有效性，在MATLAB 8.3平台上进行了数值仿真实验。1/f噪声由文献［12］提供的方法拟合生成，原始信号采用两个不同频率 f1=1 000 Hz,£¬f2=1 500 Hz的正弦信号之和：

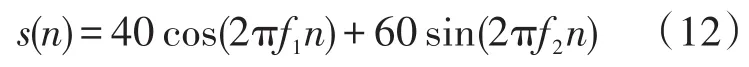
于是输入信号：f(n)=s(n)+x(n)+w(n)，其中x(n)为1/f噪声，谱参数γ=2H+1=2.6，w(n)为高斯白噪声，数据采样点数为512。小波基选择Daubechies10正交小波，最大分解尺度为4，根据式（11）算出每层的阈值分别为：λ1=138.356，λ2=100.378，λ3=97.245，λ4=96.841。

为了定量的分析改进算法的有效性，本文采用信噪比（SNR）与均方根误差（RMSE）作为评价指标来检验改进算法是否优于传统的阈值算法，其定义式分别为：

式中，N为采样点数，s（n）为原始信号，s^(n)为滤波后信号。SNR越大，RMSE越小，说明信号的整体去噪效果越好。本次实验评价指标测试结果如表1所示。原始含噪信号信噪比为4.5 dB。

表1 滤波评价指标测试比较

表1表明本文算法比Donoho阈值滤波算法使得信噪比提高了8 dB左右，且均方误差得到了一定的减小。

图2为滤波前1/f分形噪声、原始信号与叠加1/f噪声后的输入信号，图3为采用Donoho提出的阈值滤波与本文改进阈值滤波后的信号图形比较。

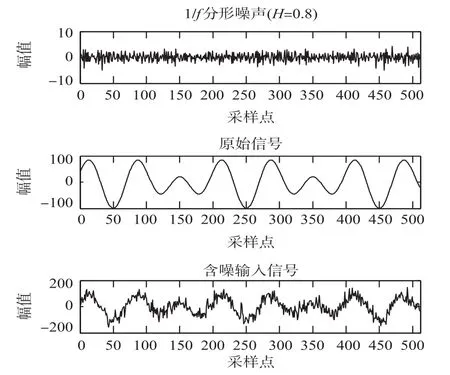
图2 滤波前信号图形比较

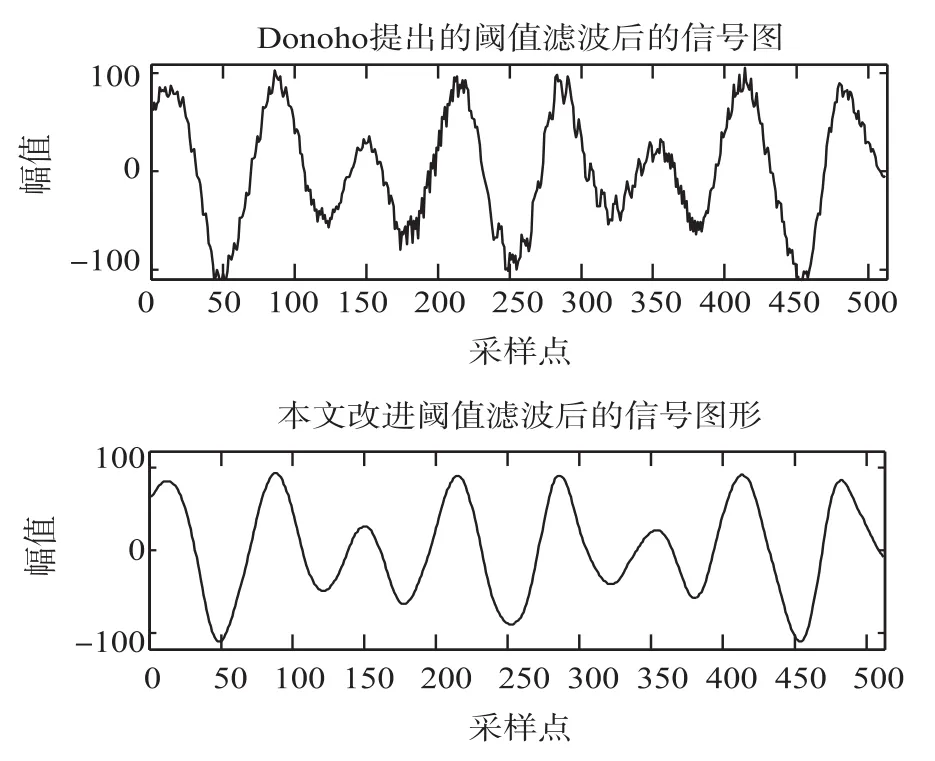
图3 滤波后信号图形比较

为验证上述算法对MEMS加速度计输出信号噪声消除的有效性，在MATLAB 8.3平台上，对本实验室设计的MEMS加速度计BJ1表头的输出电压进行多尺度自适应阈值滤波处理。采集点数为705。计算各尺度阈值之前，先采用文献［13］提出的1/f分形信号参数估计方法对输出信号的1/f噪声的谱参数γ及方差进行估计，估计值为γ=2.7，=5.3×10-8。加速度计输出信号去噪前后图形比较如图4所示。

图4 MEMS加速度计输出信号滤波前后对比

4 结束语

在MEMS加速度计系统中，加速度传感器以及测试电路引入的1/f分形噪声影响了整个系统的精度与灵敏度。本文根据1/f分形噪声的小波变换系数特性，提出了一种多尺度自适应阈值滤波方法来消除1/f分形噪声并恢复有用信号。本文先从原理上阐述了其可行性，并通过算法仿真验证了它的有效性，最后再将该算法运用到真实MEMS加速度计输出信号中，仿真结果表明，该方法行之有效。

［1］Wornell G W.Wavelet-Based Representations for the 1/f Family of Fractal Processes［J］.Proceedings of IEEE，1993，81（10）：1428-1450.

［2］赖吉强.1/f噪声小波分析软件及长程相关性研究［D］.西安：西安电子科技大学，2008.

［3］刘清君，叶伟伟.小波变换在神经细胞传感器信号去噪中的应用［J］.传感技术学报，2009，11（22）：1586-1590.

［4］马玉良，许明珍.基于自适应阈值的脑电信号去噪方法［J］.传感技术学报，2014，27（10）：1368-1372.

［5］Tewfik A H，Kim M.Correlation Structure of the Discrete Wavelet Coefficients of Fractional Brownian Motion［J］.IEEE Transac⁃tions on Information Theory，1992，38（2）：904-909.

［6］邵鸿翔，高宏峰.改进小波阈值去噪方法处理FBG传感信号［J］.激光与红外，2014，44（1）：73-76.

［7］胡英，杨杰，周越.基于多尺度Wiener滤波器的分形噪声滤波［J］.电子学报，2003（4）：560-563.

［8］Donoho D L.De-Noising by Soft-Thresholding［J］.IEEE Transac⁃tion on IT，1995，41（3）：613-627.

［9］Hui Wang，Zijian Cheng.Research on Wavelet De-noising Meth⁃od Based MEMS Accelerator Signal［R］.Proceedings of the 2010 IEEE International Conference on Information and Automation.2010：2001-2004.

［10］王丽萍，李醒飞.一种用于磁流体陀螺微弱信号检测的小波降噪方法研究［J］.传感技术学报，2014，27（10）：1355-1362.

［11］王爱萍，王惠南.基于小波分析的1/f噪声降噪［J］.数据采集与处理，2006，21（2）：217-221.

［12］孔彤.小波分析在分形信号中的应用［D］.重庆：重庆理工大学，2011.

［13］冯建昌.高斯白噪声背景下1/f分形信号波形与参数估计方法研究［D］.吉林：吉林大学，2011.

童姣叶（1990-），女，硕士研究生在读，MEMS加速度计噪声消除算法研究，369851431@qq.com；

李荣宽（1980-），男，博士，副教授，从事混合信号集成电路设计研究与教学，wilson2799@gamil.com。

MEMS Accelerometer Noise Elimination Based on Wavelet Analysis

TONG Jiaoye，LI Rongkuan*，DU Wei
（School of Electronic Engineering，University of electronic science and technology，Chengdu 611730，China）

The MEMS accelerometer has poor effects on SNR and sensitivity because desired signal is often flooded by interference and noise，especially by 1/f noise inside MEMS accelerometer system.Due to some special proper⁃ties showed by 1/f noise in the wavelet domain，time-frequency and scale analysis functions owned by wavelet analy⁃sis，wavelet analysis can be served as an effective tool for 1/f noise cancellation.An adaptive threshold filtering algo⁃rithm based on wavelet analysis is presented in this paper.The final results show that the proposed adapted thresh⁃old filtering algorithm has perspective of higher SNR and lower RMSE compared to Donoho threshold filtering algo⁃rithm and is effective on MEMS accelerometer noise elimination.

MEMS accelerometer；1/f noise；wavelet analysis；adaptive threshold filtering

TN911.4

A

1004-1699(2015)10-1503-05

��7230

10.3969/j.issn.1004-1699.2015.10.015

2015-05-20 修改日期：2015-07-20