路基曲线段土方计算偏差分析及修正

潘 丹,黄志才,彭晓彬

(湖北省交通规划设计院,武汉市 430051)

路基曲线段土方计算偏差分析及修正

潘 丹,黄志才,彭晓彬

(湖北省交通规划设计院,武汉市 430051)

公路项目中路基土方通常采用断面法,但对不规则线形段如曲线、互通内等特殊工点,采用常规断面法计算土方会出现较大偏差,给工程造成争议甚至损失,结合高速公路项目中实例,对曲线段路基土方计算的偏差原因及修正算法进行了分析,可供类似问题提供参考。

曲线段;路基土方;算法;偏差;修正

在公路工程项目建设中,确保土方计算的准确性非常重要,它涉及到工程计量、调运方案、借土或弃土等,对工程造价有直接显著的影响。

1　常用土方计算方法

常用的土方计算方法有断面法、DTM法、网格法等。

(1)断面法

断面法是沿某一平直方向每隔一段距离在其垂直方向测量一个断面,断面间土方量等于断面间平均截面积与截面间距的乘积。设断面间距为Li,横断面面积是A1、A2—Ai等,则填挖方体积V为:

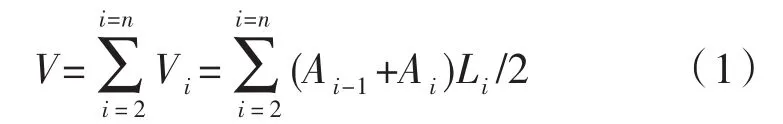
式中:Ai-1、Ai分别是第i段起终点断面的填挖方面积,Li是断面间距。

公路项目一般呈带状,路线长度较大,路基土方计算采用最普遍的是断面法,在《公路工程标准施工招标文件》规定土方是按中线长度乘以横断面面积进行计量「1],该方法具有计算方便、直观的特点,便于工程管理、计量。

(2)DTM法

数字地面模型(DTM)计算土方是利用实测地形数据进行三角构网,对计算区域土方按三棱柱法计算,累计得到指定范围内的填挖方量,实质是在坐标数据的基础上建立不规则三角网后再计算土方量。DTM土方计算方法可分为3种:根据坐标文件计算、根据图上高程点计算、根据图上三角网计算「2]。

DTM法对于计算某个区域内的土方有其优势,如对大面积的近似方形区域,原地面高程可通过地形图采集或测量后给定,施工后的顶面高程也需要通过模型给定,如顶面高程不规则,变化交频繁,则指定施工后的顶面高程工作量也较大。目前公路项目多为带状,路基宽度、填挖高、填挖边坡率都在不断变化,采用DTM法工作量较大,且计算过程不直观,不方便随土方施工进度逐次计量。

(3)网格法

该方法是将地面划分为若干个规则矩形块,原则是细分到使每个网格对应的地面高程相等,通过地表单元来划分体积单元,每个体积单元的地形被简化为四棱柱体,其高程通过空间插值来确定「3]。常见的方格网边长为5～20 m,在复杂地形区域,网格尺寸需适当划小以保证精度。

网格尺寸越小,精度越高,但会大量增加计算量;该方法点适用于较大面积的场区土方计算,而对公路这种带状体,由于各桩号处设计标高不一致,拟合出施工后的各个桩号路基断面形状工作量很大,计算过程不直观,不利于计量管理。

因此,在公路项目中,目前使用最广泛的还是断面法。

2　曲线段土方计算的偏差

对不规则线形段如曲线、互通内等特殊工点,采用常规断面法在有些情况下会有一定偏差。特别是断面左右面积不等,导致断面形心与路中线偏离较远时,偏差相对较大。

2.1曲线段

(1)常规断面算法:如图1示为某互通匝道横断面,横断面按道路中线分为左右两部分,面积分别为S左、S右,假设其该段平面近似为一圆形,半径为r,则圆周长即为路线长度,按常规断面法计算匝道填方体积:

图1　曲线段路基断面示意图

(2)将左右断面分解算法:假设S左=S右,将断面分为左右两部分,且各自以面积形心为中线分别计算体积再累计,则体积为:

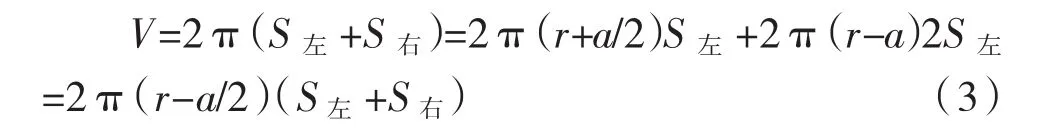
即总体积为以该完整断面的形心为道路中线,按断面法计算出的结果,相当于将路线长度(即断面间距总和2πr)按实际行心所在位置折减为2π(r-a/2)。从上可看出,式(2)、(3)是有明显差异的,则左右面积差别越大,则a值越大,土方总量偏差越大。

2.2互通内封闭区域

如单喇叭互通、苜蓓叶形式互通环圈匝道半径多为55～60 m,环圈内部设计时从景观、排水等因素考虑多需整平至某标高,目前常用有2种方法:

(1)近似法:按面积与平均填高、挖深之积来估算土方数量;因平均填挖确定人为偏差较大,特别是地面凸凹不平时,最后结果偏差很大,且该方法无法在路基断面中直观体现出来。

(2)断面法:将环圈内部分也体现在路基逐桩横断面中,则匝道内侧的路基断面宽度即为环圈半径,如图2示,该方法将环圈内土方进行了量化,相比近似法更直观,利于施工控制。但也存在2.1节提到的问题,应根据情况对断面面积或路线长度进行必要折减。

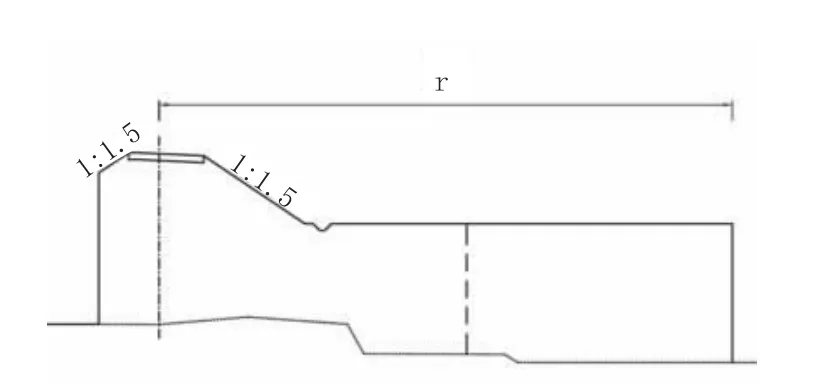
图2　环圈匝道路基断面示意图

3　传统断面法的修正

3.1修正后的断面算法

从式(2)、(3)可看出,采用传统断面计算曲线段土方是有明显偏差的,根据前述分析,提出两种修正方法,可得出近似精确的计算结果。

(1)修正算法1

断面面积不变,将桩间距折减,即将路线中线长度进行折减,折减至面积实际形心位置,折减系数λ=折减后路线长/折减前路线长。如图1中,折减后的中线长是个比r小的圆周。

(2)修正算法2

由表5可知，级配碎石基层竣工后其横坡度平均值为0.15%，可以满足规范要求，级配碎石基层在施工时对横坡度指标的控制良好。

路线中线长度不变,考虑曲率将断面面积进行折减,即断面面积乘以折减系数λ;最终折减效果与方法1相同。如图2中,折减后虚线右侧的面积不再计入断面面积中。

考虑路基土石方表直观,便于利用程序自动计量,对曲线段土方一般采用方法2进行修正计算。

3.2计算案例

结合笔者参与设计的部分高速公路设计中的土方计算分析如下:

(1)枢纽互通小半径匝道

麻城至武穴高速公路团破枢纽互通为全苜蓓叶十字枢纽,互通填方总量为199万m3、挖方数量为192万m3。其中有四个环圈匝道A、B、C、D,见图3，匝道圆曲线半径均为60 m,环圈匝道内侧为填方,平均填土高度为10～12 m,设计时采用修正断面法计算土方,将环圈内侧断面面积进行了折减,折减系数约为0.5。

图3　枢纽互通内小半径匝道示意图

分别按传统断面法、修正断面法、数字地面模型3种算法计算这4条匝道的土方结果见表1。

表1

表中DTM法采用数字地面模型进行核实的结果,利用EICAD软件的数模土方计算功能,将互通内环形匝道填筑区域模拟为一个顶面底面均为曲面的柱体(对顶面曲面指定高程点、对底面曲面由测量点指定高程),是相对较准确的结果。从表中可看出,修正断面法的精度远远优于传统断面法,如采用传统断面法,按合同单价将多支付约254万工程费。

武汉至鄂州高速公路鄂州东互通为单喇叭互通,受地形地物限制,环圈匝B内部为一山体,中线最大挖深为26.7 m,匝B中线圆曲线半径为57.5 m,见图4。考虑匝B内挖方量大,设计时未将环圈内整平至某个标高,而是按1:3坡率的设置挖方边坡,挖方体积按修正断面法计算,考虑了折减系数。如断面面积不进行折减,将路基断面中线右侧的断面宽度取半径即57.5 m,则会多计挖方约5万方。

4　结语

断面法是路基土方计算中的常规算法,方便直观,使用广泛。在实际工程中,曲线段路基土方计量易出现明显偏差,特别是满足以下曲线半径较小和断面中线左右两侧面积偏差较大两个条件时。在工程实践中该问题并没有广泛出现,主要是因为高速公路圆曲线半径一般比较大,如速度100 km/h对应的主线最小圆曲线半径R=700 m,可近似认为是直线;另外,对大部分断面来说,中线左右侧的填挖方面积偏差不是特别大。但对互通匝道等特殊路段,这种情况还是普遍存在的。

图4　一般互通内小半径匝道示意图

当出现满足以上两个条件的工点时,需引起注意,传统断面法计算土方量的局部偏差甚至可达50%,本文提出了一个修正断面法的思路,即通过调整中线位置、或调整中线两侧的填挖断面积,引入修正系数,修正后的断面法消除了传统断面法的偏差,使得断面法用于土方计量的准确度大为提高,且直观方便,可供类似特殊工点土方计算提供参考。

「1] 公路工程标准施工招标文件「M].北京:人民交通出版社,2009.

「2] 涂群生.利用建立坐标数据文件的方法计算土石方量「J].测绘通报,2007(8):45-47.

「3] 王先鹏,曹荣林.土方量计算的原理与方法及ArcGIS的应用前景「J].地理空间信息,2009，7(4):139-141.

U416.1+11

B

1009-7716(2015)12-0030-03

2015-08-05

潘丹(1982-),女,湖北黄冈人,工程师,主要从事公路工程的设计及研究。