港区道路出入口喉深长度设计方法仿真研究

朱先智

(深圳市城市规划设计研究院有限公司,广东深圳 518031)

港区道路出入口喉深长度设计方法仿真研究

朱先智

(深圳市城市规划设计研究院有限公司,广东深圳 518031)

港口是货流集散中心,多为公路或者城市道路的起迄点,并具有不同的交通特性。在港区道路出入口处由于衔接不畅容易产生交通安全、交通延误问题。分析港区道路出入口交通特性,建立仿真模型;分析喉深长度与控制延误时间的对应关系,确定港区道路设计合理喉深长度,确保行车安全、顺畅。

港区道路;出入口;喉深长度;设计

0　引言

近年来,港口外贸额在国民经济所占份额日益提升。新港规划设计、旧港改扩建成为重点工程,但设计方法沿用城市道路理论,制约港区道路效益发挥,其中衔接港区设施内部道路和港区道路的出入口处矛盾最为突出,易发生车辆排队、阻塞延误。合适的喉深长度起着联系、过渡和流线转换的作用,协调土地开发与交通需求的保证,是港区出入口设计主要技术指标,而对于港区道路喉深长度设计一直沿用城市道路研究成果,缺乏针对性研究。

1　港区道路出入口交通特性分析

对于港区内的物流公司堆场和保税区等设施区域,交通需求产生于货物运输的需求,而非基于人的出行,港区道路的主要交通参与者是运载货物的卡车及少量的办公车辆和工程车辆,几乎没有步行者和自行车。

2　港区道路出入口喉深长度建模

以接入码头大门为界,将外部抽象为一个T型交叉口并划分为3个区域:T型交叉口区域、接入道路区域、接入单位内部冲突区域,如图1所示。假定车辆到达分布为泊松分布,车辆到达的时间间隔服从负指数分布,根据车辆的行驶路线绘制行驶轨迹,并按大小划分元胞,利用一维元胞自动机模型对该区域的交通流进行描述。

图1　仿真模型示意图

2.1初始化模型［1］

(1)车辆类型

由于港区设施交通特性,进出物流公司码头堆场和保税区等区域的车辆都是大型集装箱车,设定与路段3有关的车辆全部为大型集装箱车。在主路直行车流中加入一定比例的小型车。

(2)驾驶员类型

本文将港区驾驶员分为3种类型:激进型、一般型和保守型。区别主要体现在:车辆加减速度、临界间隙、期望间距、随机慢化概率、最大速度等几个方面。

(3)行驶目的地

对于进出接入单位的车辆需要赋予目的地属性,用于确定车辆在路段3是否需要转换车道。

2.2交通冲突模型［2］

(1)交通流优先次序

在T型出入口处交通流分为3个优先等级,见图2。等级1:流向1、2、4,即主路直行交通和主路右转交通;等级2:流向3、6,即主路左转交通和次路右转交通;等级3:流向5,即次路左转交通。等级低的车流要给等级高的车流让路或让行。

图2　T型交叉口交通流等级示意图

(2)临界间隙和跟车时间

临界间隙是主路交通流中可提供次路一辆车驶入交叉口的最小时间间隔,计算值根据实验观测的最大拒绝间隙和最小接受间隙确定。美国临界间隙计算方法:

式中:tc-x为交通流向x的临界间隙,s;tc0为理想临界间隙,s;te为修正参数,当车流为次路左转时,该值为1.7,其它情况为0。

当次路车流为饱和流时,即该车流行驶速度较低,车头间距较小,速度趋于一致,次路中相邻两辆车使用主路同一间隙驶离交叉口的时间,称作跟车时间。若高等级的流向没有冲突车辆时,跟车时间为该车道饱和流率的车头时距。计算公式如下:

式中:tf-x为次路交通流向x的跟车时间,s;tf0为理想跟车时间,s。

2.3车辆运行规则［3］

2.3.1最大速度

由于驾驶员及车流的不同,最大车速也不同。

2.3.2期望间距

车辆的跟驰行为主要受与前车间距大小的影响,当车辆与前车的间距大于期望间距时,车辆会加速,当车辆与前车的间距小于期望间距时,车辆会减速。公式如下:

式中:h为期望间距;L为前车的车身长;q为跟驰车驾驶员的敏感系数,激进型取0.9,一般型取1,保守型取1.1;vt为跟驰车的运行速度;ut为前车的运行速度;b为待定常数。

当前车为重型卡车时,用DL(Discomfort Level)来衡量跟驰车辆的不适度,期望间距的模型为:

式中:β为不适度的影响系数,取值为8.15;DL的取值范围为1～1.6。

车辆换道时还要考虑与目标车道后方车辆的距离,其可用前车期望间距乘以调整系数λ估计,即。

2.3.3直行车流的车辆加速度

式中:xt+δ为前车在时刻t+δ的位置;yt为跟驰车在时刻t的位置;q为驾驶员对前车的敏感度衡量因子。

前车为重型卡车时,跟驰车辆的加速度为:

2.3.4转弯车流的车辆加速度

加速度干扰值越大,驾驶员所采取的减速度也越大,两者存在非线形的正相关关系。当加速度干扰值超过0.7时,应考虑加速度干扰对驾驶员减速度的影响。根据车辆性能,加速度设置为:

式中:acure-car为前方车辆为小汽车时的车辆加速度; acure-truc为前方车辆为重型卡车时的车辆加速度;σ表示加速度干扰值。

2.3.5运行规则

针对港区设施接入道路出入口仿真模型,建立车辆的运行规则如下。

(1)跟驰规则:设置车辆加速度、随机减速,限制最大最小车速。

(2)换道规则:根据车辆是否在目标车道上行驶判断车辆是否存在变换车道需求,并根据与目前车道前车、跟驰车的期望间距判断是否存在变换车道的条件。

(3)避让规则:在无信号出入口处,根据车流优先次序确定优先规则。

(4)信号交叉口规则:根据信号交叉口通行规则,设置车辆满足安全、舒适条件下的运行规则。

3　港区道路出入口喉深长度仿真实验

3.1无信号交叉口仿真实验［3］

在仿真区域内,按照前述冲突模型建立优先行驶规则,喉深长度由50 m变化到150 m,仿真时长选取10 000 s,仿真不同流量组合条件对应的控制延误时间。

观察图3,可得到如下结论。

图3　不同流量组合条件下喉深长度与控制延误时间关系

(1)当主路与接入道路交通流量都达到饱和时,即流量组合为(1 200，700)时,控制延误时间一直都保持在一个较高水平,与喉深长度关系不大,说明在这种情况下加长喉深长度不能有效提高接入道路的通行能力和服务水平,需要考虑其它组织方式,如禁止车辆左转或加设信号灯控制等。

(2)在既定的流量组合条件下,控制延误时间与喉深长度成反比,即喉深长度越长,则控制延误时间越小;喉深长度越短,则控制延误越大。

(3)当流量较小时,喉深长度对控制延误有较大的影响,如交通流量组合(1 200，500)情况下,喉深长度为100 m时趋于缓和。

3.2信号交叉口仿真实验［3］

在仿真区域内,设置信号周期时长为90 s,每个相位时间为30 s,设置喉深长度由50 m变化到150 m,得到不同流量组合条件对应的控制延误时间。

观察图4可以得出如下结论。

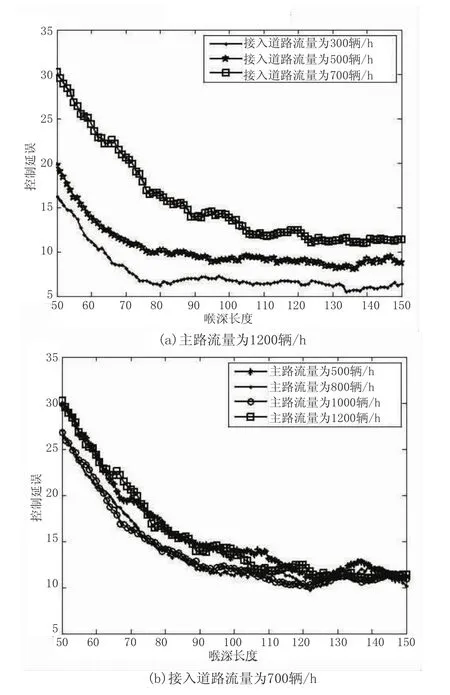
图4　不同信号周期喉深长度与控制延误时间关系

(1)从整体趋势上来看,同无信号交叉口的结论是相同的,即喉深长度越长,控制延误时间越短,并且在降低到一定数值时趋于平缓,说明喉深长度的增加可以降低控制延误时间,但是超过到一定值时,效果明显降低,应该考虑其它措施,如改变信号周期,禁止左转等交通组织方式。

(2)主路流量一定时,接入道路流量越小,车辆控制延误时间越短。

考虑信号周期对控制延误时间的影响,选取90 s,60 s,30 s三种信号周期,确定主路与接入道路的流量组合为(1 200、700),分别进行仿真实验,得到喉深长度与控制延误时间的关系如图5所示。

观察图5知,当信号周期增加时,控制延误时间减少,即信号控制交叉口处信号周期不宜设置过短,会导致车辆的延误。

4　结语

本文针对不同信控条件,采用仿真模型对不同主路、接入道路流量组合条件下描述控制延误时间与喉深长度的关系,得到:(1)喉深长度不适合饱和交通流;(2)非饱和交通流条件下,控制延误时间与喉深长度成反比;(3)喉深长度存在适度值,超过适度值时对降低出入口控制延误时间效果不明显。

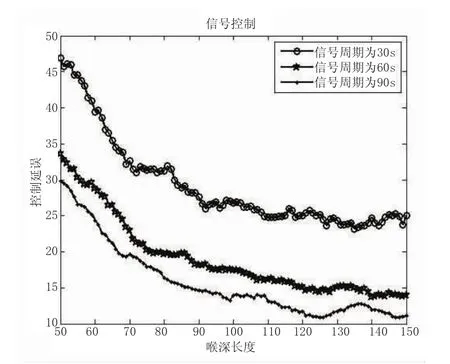
图5　不同信号周期条件下喉深长度与控制延误时间关系

「1] 周骊巍，白子建.港区道路交通行车安全分析「J].城市道桥与防洪，2010，(12):15-17.

「2] 贾斌.基于元胞自动机的交通系统建模与模拟「M].北京:科学出版社，2007.

「3] 康迪.港区道路出入口设计的仿真研究「D].天津:天津大学，2012.

U412.37

A

1009-7716(2015)12-0009-03

2015-06-06

朱先智( 1962-) ,男,贵州兴仁人,副总工程师,高级工程师,现从事市政交通规划设计工作。