构建衔接视野下的PBL数学教学模式
庄惠芬
儿童在数学学习过程中要经历小学—初中—高中这样的发展阶段,新课程实施以来,为了促进各学段之间的衔接,九年义务教育分为三个学段,名称也相应地改为第一学段—第二学段—第三学段,数学内容的四个领域和课程目标也有了衔接。但是在具体实施过程中,教材编者各自为政地编写、实施教学的教师也独自在自己学段进行研究,因此课程实施过程中出现了断层、脱节、重复等现象。我们常常觉得学生的问题解决意识与问题解决能力弱,这是因为每个学段的编者和教者都没有一种整体的视野,缺少一种从衔接视野的角度进行数学教学模式的构建。
PBL是Problem-Based Learning(基于问题的学习)的缩写,是一种以问题为驱动力和以培养学习者问题意识、批判性思维技巧以及问题解决的实践能力为主要目标的学习。(胡庆芳、程克拉语)对学生而言,在数学学习中,大抵都要经历问题情境—数学问题—建立模型—解释拓展应用—检验等这样的过程。发现问题、提出问题、分析问题、解决问题也成为新课程标准中的“四能”。如果能以PBL理念下基于问题的学习作为儿童数学学习衔接的载体,那么通过对教学内容、教学方式与思维方式进行有机整合和衔接,形成可操作的衔接策略,就能促进儿童数学素养的发展。
一、衔接学科本质,重塑PBL数学教学的特点
PBL教学应用在数学中,主要是培养学生的数学素养,即有数学知识、数学技能、数学能力和数学态度。其中数学能力主要是数学思维能力,还包括应用数学方法观察、分析和解决实际问题的能力;数学态度则是相信数学,热爱数学,用数学的态度以及大胆创新的态度,使其真正做到数学来源于实践,应用于实践。
1.情境性
基于问题学习,采用有趣的方式(如浏览图片、欣赏音乐、观察实物、故意设疑、谈话引导、现场游戏、案例分析、讲故事、做实验等),巧妙地创设问题情境。注重把学习置于具有挑战的、有意义的问题情境中,让学生去经历、去感悟、去观察、去理解、去认识,最终掌握之;让学生通过合作探索解决实际问题,形成解决问题的方法与策略,建构数学模型,获得自主学习的能力与数学思维的发展。
2.体验性
PBL数学教学模式主张以问题为载体并贯穿整个教与学的过程中,在实践中不断优化自主学习方法。这种教学方式要求学生亲身体验数学活动,让他们积极进行探究和创造性思维活动,使“主体”真正地主动联系已有的知识、技能、经验,进行有理有据的猜想、推理,一丝不苟地研究、分析,不拘一格地创想、创造,在这个过程中不断变换角度、思路进行审视、调整,自我否定、自我修正。在这个过程中认识到现实生活中的实际问题,面对实际问题,组织学生采取板演、讲解、对话、挑战、辩论、评价等多种形式展示交流,彼此思维碰撞,点燃创新火花,建立合适的数学模型,用积累的解决问题策略、数学活动经验探索其应用价值。
3.思维性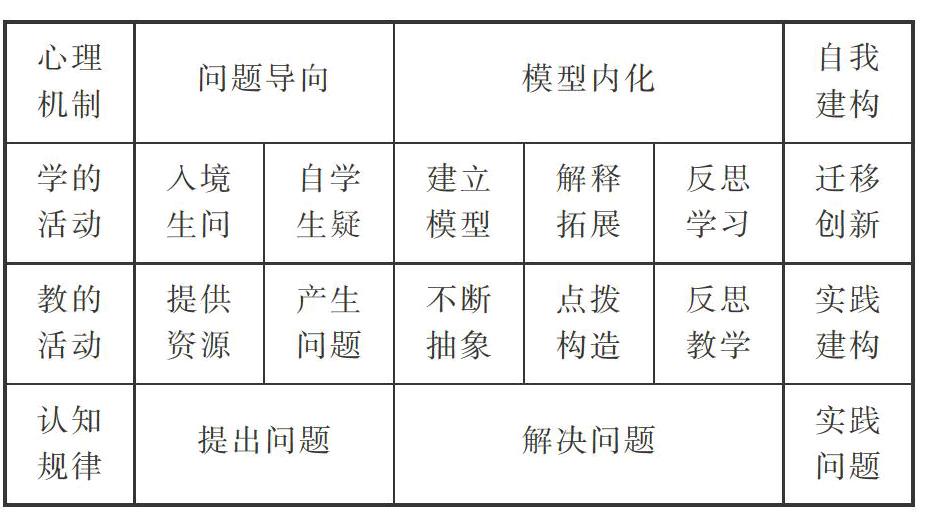
在PBL数学教学模式的建构中,真正让学生得益的是获得数学的思想精神、浸润数学的文化力量、习得科学的数学思维方式。在问题解决过程中,通过观察、猜想、实验、推向、归纳、类比等过程获得探究的思想与思路,并能进一步验证、拓展和应用。在这个过程中,引导学生有条有理地表达、有根有据地探索,运用数学语言进行合乎逻辑地质疑和思辨。在这个过程中,不仅获得知识,更多的是获得一种思维方式,做到心中有数、自我完善、自我激励。
4.模型化
广义地说,数学即模型,基于PBL理念下的问题解决过程就是学生针对数学概念、规律等特征,以及数量间的关系,进行建立模型的过程。因此基于PBL理念下的数学教学,是从学生已有的生活经验出发,不断经历问题情境—建立模型—解释:对模型求解—应用与拓展的过程。儿童经历的这个过程就是对数学模型建立、理解、运用、把握的过程,利用数学的思想方法、知识技能、经验策略解决问题的过程。
5.思想性
在PBL理念的指导下,我们看到的是数学学科本质的充分体现,理趣与情趣的交融、思维和思想的生成。“求真”:让学生拥有数学的头脑,从数学中寻找真理的力量,放手让他们自己去实验、自己去争辩、自己去探索,学会从数学的角度思考问题。“臻善”:汲取数学的精神养分,让学生从理性精神中汲取力量,从历史演进中汲取力量。“尚美”:分享数学世界的美妙、数学方法的优美、解决问题过程中思路的简洁、不同视角的独特、不同方法的殊途同归、探索过程的一波三折、问题结果的出人意料。
二、衔接课程旨归,重觅PBL数学教学的内容
“衔接”是按照数学课程目标的内在联系,将数学课程内容进行核心内容的梳理、思维方式的有机结合,在这过程中关照知识的衔接、心理的调适、方法的指导、行为的跟进、思想的顺应、生活的适应,建构促进儿童可持续发展的课程内容和教学素材。
1.立足数学模型解读内容
(1)从局部到整体。从知识的一棵树到体系的一片林,我们往往是一课时一课时展开教学,却忘记背后的体系,所以解读内容需要有结构化的眼光、体系化的视野。
(2)从意义到结构。数学即模型,数学即抽象了的结构,在儿童理解数学的意义基础上需要进行必要的抽象和模型建构。
(3)从结构到思想。按照具体情境,经历探索过程,建立模型,解释拓展运用。让学生借助直观体验,进行猜想、举例验证,运用多种策略解决问题。
(4)从探究到应用。在基于问题解决的数学学习中,注重的是解决问题的情景和背景,让学生经历数学的发生发展过程,同时突出运用数学模型不断解释、拓展、解决新的问题。
(5)从建构到解构。在数学建构过程中,学生不断丰富和完善自己的观点和模型,并在解决问题的过程中不断取舍完善、体会结构的合理性。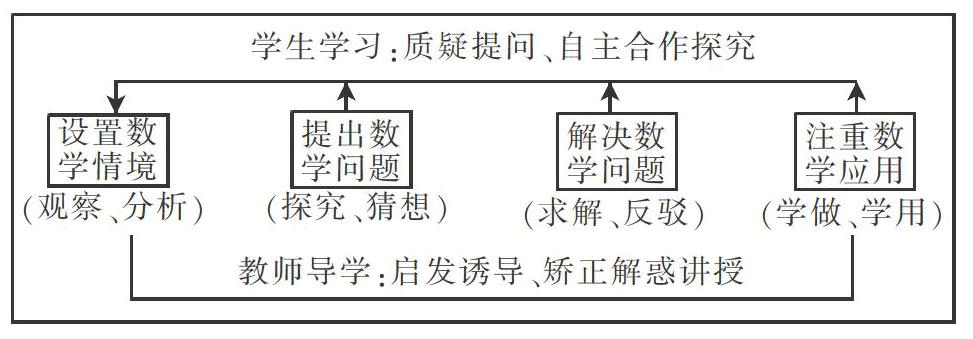
2.立足数学建模把握价值
教材对于教师与学生来说,是冰冷的文本、是静态的结果、是抽象的内容,在编排中也是一种封闭的回环的体例。小学教师要用课程的视野进行同一内容不同学段的衔接,梳理不同学段的内容脉络,将冰冷的文本化作火热的思考。
(1)从知识扩充中把握规律本质。在小学阶段的运算律教学中,有学生询问为什么有乘法运算律、加法运算律,却没有除法和减法运算律,只有运算性质呢?其实,如果用衔接的视野来看,就会发现在自然数集中,减法、除法与加法、乘法互为逆运算;如果学习了负数,那么减法不就自然变成了加法;如果学习了分数除法,除法不就转化成了乘法。因此,减法和除法的运算性质是流,而不是源。
(2)从数学模型中抽象方法模型。教材的编排有一个共同的特点,会让学生在解决问题的过程中有几种方法、几种不同的思路;在备教材过程中,对核心问题的提出非常关键,在让学生发现不同思路的同时更要让学生知道观察结果的相同,并且理清为什么结果会相同,不同中的相同,偶然中的必然。在建立模型的基础上要让学生举例验证、拓展运用,在解决新问题中发现与之前模型的相同与不同,不断经历发现问题—实验验证—得出结论—拓展应用的过程。
数学是研究数量关系和空间形式的科学,因此在衔接中要注重数与形两大方面的相互衔接,要注意在内容上的“瞻前顾后”,方法上的“上衔下接”,思想上的“左顾右盼”,着力凸现出“创设问题情境—现实问题数学化—问题解决与数学建模—应用与拓展”的逻辑结构,体现“让学生做数学、研究数学”的价值取向。
三、衔接教学程序,重建PBL数学教学的模式
PBL数学教学方式是以问题为起点,以学习者为中心,置身于真实情境中的问题式的学习。PBL数学教学方式以学生作为问题的解决者和知识能力的建构者,有学生个人、小组和集体的讨论、探索、表达的机会,是一种以自主学习为核心解决问题的教学模式。
1.基于“模型建构”的教学
PBL课堂教学的特点:重自主、重体验、重童性、重素养、重人格。基本教学模式:
[原型唤醒] → [问题简化] → [经历创造] → [协作会话] → [拓展延伸]
(1)“原型唤醒”,让学生亲身体验生活,让学生主动获取真实信息,增强学生的数学意识。
(2)“问题简化”,意义赋予,实现问题简化的过程。
(3)“经历创造”,创设一些把所学知识运用到生活实际的环境,来促进学生把数学模型建构得更好,感受数学之真。
(4)“协作会话”,主要通过儿童、文本、教师三者之间的有效协作,体悟数学之美,为儿童合理建模奠定基础,在儿童的世界里共生。
(5)“拓展延伸”,通过寻找知识与学生生活的最佳结合点,丰富儿童心智,完善儿童人格,获得数学之善。
学生在真实情境中将生活问题抽象成数学问题,不同的学生采用不同的方法,学习过程围绕问题展开,把现实生活中的实际问题所包含的数学知识、规律抽象出来,建成数学模型,让儿童在问题、挑战、挫折、取胜中交替体验,在选择、判断、协作、交流的轮换操作中经历,进而发现问题、提出问题、建立模型、解释拓展应用,走向新的学、用知识的过程。
2.基于“学习共同体”的教学
案例:有一次来家中抄天然气表的阿姨无意间说:“这个月,你家的天然气用量怎么比往常增加了?”让一凡同学产生了思考:是不是我家的天然气存在浪费现象?如何研究?
一凡和大家共同研究:在相同的条件下,煮沸相同器皿中相同水量的水,天然气的耗量与天然气点火旋钮的角度打开度是否有关系。经过多次实验,发现当旋钮开度为30°~45°和135°~150°时,天然气耗量最少。由此可以得出结论,减小天然气流量,适当延长加热时间,具有节气的效果。
这是一种类似于数学课题学习的模式,形成“基于数学、源于数学、始于课堂、源于生活”的教学模式。教学内容和教材内容紧密联系并进一步拓展深化,主要有生活问题、社会问题、实践问题三类。在这个过程中,注重数学模型的建构、数学思想的渗透,不断从单项模型深化为模型群。比如:(1)手机收费“全球通88系列套餐”选择的分析;(2)自行车与儿童身高的问题;(3)小动作大作用——谈改装后抽水马桶的节能;(4)游园路线;(5)安全疏散模型;(6)大课间学生行进的最佳路线;(7)峰谷电合算不合算?(8)红绿灯的时间分配合理吗?等等。数学模型问题应运而生。在这个过程中,不仅有数与式的运算、数量关系的抽象、数据分析的明晰、空间与图形的想象,还伴随着观察、分析、判断、分析、概括、选择、统计等诸多方面。
3.基于“模块整理”的教学
在数学教学实践过程中,我们也研制了“加减乘除的整理”“图形之间的关系”“运算律的整理”等。“数学整理课教学模式”中诸环节和心理机制、认知规律之间的基本关系可用下表表示:
这样基于问题学习的整理课,不同内容有所不同,让学生亲身经历将实际问题抽象成数学模型并进行解释与应用的过程,重在衔接模型之间的联系与沟通,即在单个模型的基础上,把相关联的各个模型构建成一个数学模块,形成一个网络式的模块体系。在这个过程中,知识的整理是载体、模型群的建立是关系、方法链的衔接为要义,要在学生的头脑中形成知识框架、方法结构、数学模型。
4.基于“情境问题”的教学
从设置数学情景—提出数学问题—解决数学问题—注重数学应用,基于问题的数学学习能够通过好问题场的设置,让儿童亲身体验、自主探究,实现“提出问题─解决问题─提出新问题─解决新问题”的螺旋式发展,获得发现问题、分析问题、解决问题的思维方式,对数学模型的建构有着直观和深刻的理解和把握。
模式的核心是问题的提出,将儿童的问题意识、问题能力贯穿于学习过程中,让儿童能从发散性提出问题—主题性提出问题—自主创设问题情境中不断发展。内在联系:创设情境是前提,提出问题是核心,解决问题是目标,应用知识是归宿。
PBL强调以学生为中心,学生学得轻松、理解得透、掌握得牢、应用得趣,创想有乐;让我们启迪智慧、开发悟性、挖掘潜能、培养能力、陶冶情操,基于问题的学习让学生享受贯通的酣畅、豁然开朗的喜悦、自主建构的兴奋、应用自如的徜徉,让课堂成为学生快乐的生命之旅!

