高速陶瓷电主轴结构设计及静动态特性分析

饶成晨 陈 涛



高速陶瓷电主轴结构设计及静动态特性分析

饶成晨1陈 涛2

（1. 浙江大学 机械工程学院 杭州 310002；2. 武汉理工大学机电工程学院 武汉430070）

高速电主轴作为高档数控设备的核心部件，其性能的优劣直接影响着加工零件的精度。针对现有某高速精密磨削加工中心，对其电主轴的材料、轴承配置形式及预紧方式等基本结构进行设计与选择，完成三维模型的建立。通过ANSYS对其刚度、强度、固有频率及临界转速等静动态特性进行分析，结果表明该结构的合理性，对该类电主轴的设计与使用具有一定的参考价值和指导意义。

有限元分析 高速电主轴 静态特性 动态特性 结构设计

进入21世纪，现代机械制造业蓬勃发展，正朝着高效率、高速度、高精度的方向不断进步。随着数控技术的广泛应用，机床高速加工技术在航空航天、汽车、材料、模具等行业迅速崛起。机床高速加工能获得机械产品较高的加工精度和表面加工质量，是现代制造业又一次革命性的飞跃。高速机床作为实现高速加工的基础设备，是现代制造业的战略性产业[1]。而电主轴作为高速机床的核心部件，成为今后机床的重点发展领域。

电主轴单元的静动态特性主要包括刚度、强度、固有频率和临界转速等，其对电主轴的精度、速度等性能有很大的影响。关于主轴静动态特性的研究，在上世纪60年代，一般采用经验类比法来进行选择主轴参数、设计主轴结构，计算精度低[2]。

而近20年来，随着计算机技术和计算策略的不断改进，出现了有限单元法、传递矩阵法、模态法、结构分析法等大量计算方法[3]。其中，在简化模型的基础上，通过有限元分析的方法已经逐步发展起来。利用动静态有限元分析的方法，可以从仿真模型中判断出电主轴各部件结构的合理性及高速机床存在的薄弱环节[4]，依据这些数据在设计电主轴参数时进行相应的改进，从而改善高速机床的性能，提高其加工精度和产品质量。

本文以某精密磨削加工中心电主轴为研究对象，分析其基本结构及原理，并应用三维机械设计软件Proe进行整体结构设计建模；通过有限元软件Ansys将三维电主轴模型划分为有限元模型，进行静动态特性的仿真分析。

1 电主轴结构设计

随着加工技术的进步和新型材料的不断涌现，氮化硅(Si3N4)陶瓷在电主轴上的应用逐渐扩大，其具有硬度高、耐高温腐蚀、密度小、线膨胀系数低、弹性模量大、不导电及不导磁等优点，与传统的钢制材料相比，在高速旋转下主轴以及轴承产生的离心力小、热量少，能在很大程度上提高高速电主轴的工作性能，使其具有更高的速度和更大的转矩，因此本文主轴单元选定为陶瓷高速电主轴。

高速电主轴是一个完整的系统，其组成部件主要包括轴壳、转轴、轴承、定子与转子、润滑系统以及冷却系统等，某精密磨削加工中心电主轴系统总体结构装配图如图1所示。

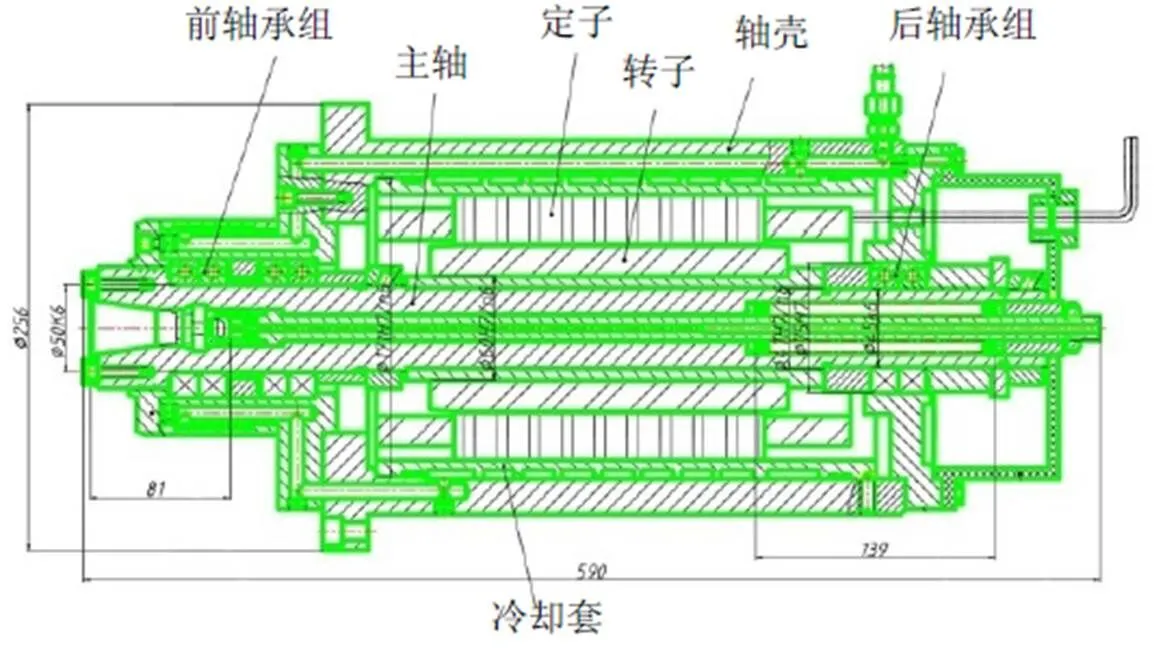
图1 高速电主轴装配图

1.1 轴承的选用

1）轴承类型

高速轴承是电主轴实现高速、高精度的核心部件。当电主轴高速运转时，轴承会受到载荷冲击和内部的剧烈摩擦[5]。因此，在选择电主轴轴承时，必须考虑该轴承动负荷承载能力和高速性能，除此之外，还需保证轴承径向、轴向刚度和有较低的温升。而陶瓷球轴承具有重量轻、弹性模量高、寿命长、膨胀系数低、硬度高、耐高温、热导率低、结构简单的特点，符合高速电主轴的需要。

2）轴承材料

对比Si3N4陶瓷和轴承钢两种材料性能，其中Si3N4陶瓷的密度仅为轴承钢的40%，而弹性模量、硬度、热导率、线膨胀系数以及极限温度值也明显更优[6]。

3）轴承结构

按轴承的结构分类，轴承可以分为角接触球轴承、调心球轴承、深沟球轴承、推力球轴承、推力调心滚子轴承、圆柱滚子轴承、圆锥滚子轴承和推力滚子轴承等，其中角接触球轴承通常成对使用，且极限转速较高，适用于转速高、同时承受径向和轴向载荷的场所[7]。

根据以上的分析，本文电主轴采用陶瓷角接触球轴承为支撑轴承。

1.2 轴承的配置方式

因为电主轴的转速较大，而角接触球轴承接触为点接触，刚度比较低，所以为了提高轴承的刚度和承载能力，考虑用多个轴承组配的形式使用。多联组配能够提高主轴系统的刚度，但轴承组配数过多会限制电主轴达到最高转速，同时每个轴承的误差会累加[8]，因此，该电主轴的前轴承选用成对串联的背对背(QBC)配置形式，后轴承选用双联组配的背对背(DC)配置形式，两端能同时承受较高的倾覆力，如图2所示。

图2 电主轴轴承配置形式

1.3 轴承预紧

轴承预紧的方式主要有径向预紧和轴向预紧两大类。其中径向预紧法多用在承受径向载荷的圆锥轴承中。而轴向预紧主要有定位预紧和定压预紧两种方式，本文采用轴向预紧中定位预紧方式进行轴承预紧：采用定位预紧时，轴承径向刚度随着转速的增加而增加，而轴向刚度和角刚度随着转速的增加呈先大后小的趋势变化[9]；轴承高速运转时，定位预紧的轴承刚度值要比定压预紧的轴承刚度值更大[10]。

综上所述，本文电主轴选用陶瓷角接触球轴承；配置形式采用前轴承为成对串联的背对背(QBC)的方式，后轴承采用双联组配的背对背(DC)的方式，前支撑轴承型号为7010C/HQ1P4QBC，后支撑轴承型号为7009C/HQ1P4DB；预紧方式采用定位预紧，前后轴承的预紧力分别为152.2 N和112.5 N，主要技术参数如表1所示：

表1 前后轴承主要参数

1.4 电机选择

除此之外，选用油气润滑方式和油水热交换循环冷却系统，确定了本文研究的的高速陶瓷电主轴的整体结构的设计，三维模型如图3所示。

图3 高速陶瓷电主轴三维图

2 主轴系统受力分析

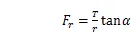
3 静力学分析

3.1 主轴结构简化条件

本文利用ANSYS对该高速陶瓷电主轴进行静力学分析，电主轴实体模型采用SOLID185单元，轴承则采用COMBIN14弹簧-阻尼单元，而简化条件为以下四个：(1)将电主轴的主轴、转子、定子及套筒作为一个整体处理，且其材料均布且属性相同，等效到所有的主轴单元上[11]；(2)将所用的角接触球轴承简化为弹性约束，两个相邻的串联轴承采用一个弹性单元表示，且只考虑径向力；(3)轴承的支承点在接触线与主轴的轴线交点处[11]；(4)弹性单元刚度用轴承径向刚度表示，且忽略轴承负荷及转速对轴承刚度的影响，并视轴承刚度为定值[12]。

3.2 有限元模型建立

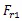
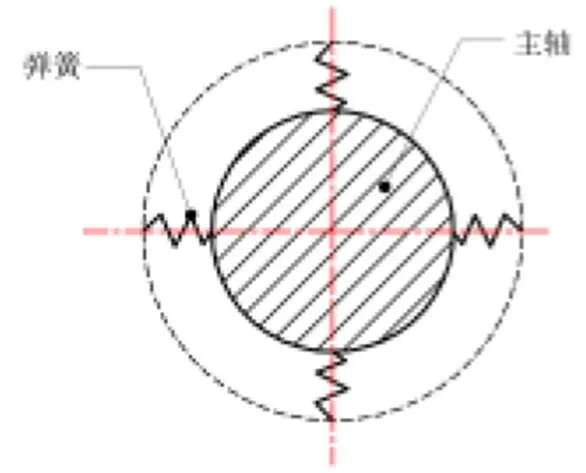
图4 轴承有限元模拟图

图5 施加载荷后有限元模型

3.3 电主轴刚度分析

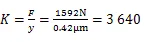
远远大于一般高速电主轴所要求的刚度值300 N/μm，满足使用要求。

3.4 电主轴强度分析

主轴材料为Si3N4，其抗弯强度为[]=700 MPa，查看该电主轴的环形应力云图，如图7所示，可得电主轴上的最大应力为max=112.1 MPa，小于材料的许用应力[]，所以该电主轴的强度满足使用要求。

图7 电主轴环形应力云图

4 模态分析

电主轴模态分析的基本有限元模型与静力分析时的大体相同，各项属性均不变。本文采用常用的分块法(Block Lsnczos)模态提取法，取该电主轴前6阶模态进行分析。

4.1 固有频率及振型图

该电主轴的前六阶模态固有频率如表2所示：

表2 电主轴前六阶模态固有频率

六阶模态的振型图如图8所示。从表2可以看出，一阶和二阶模态的固有频率很接近，且从图中能看出振型图表现为正交，两者固有频率可以作为重根；同理，四阶和五阶模态的固有频率也为重根。

4.2 临界转速

主轴的临界转速和频率的关系为:

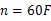
式中：为主轴转速(r/min)；为频率，单位为Hz。

则该电主轴的临界转速表如表3所示：

表3 电主轴前六阶模态固有频率及对应的临界转速

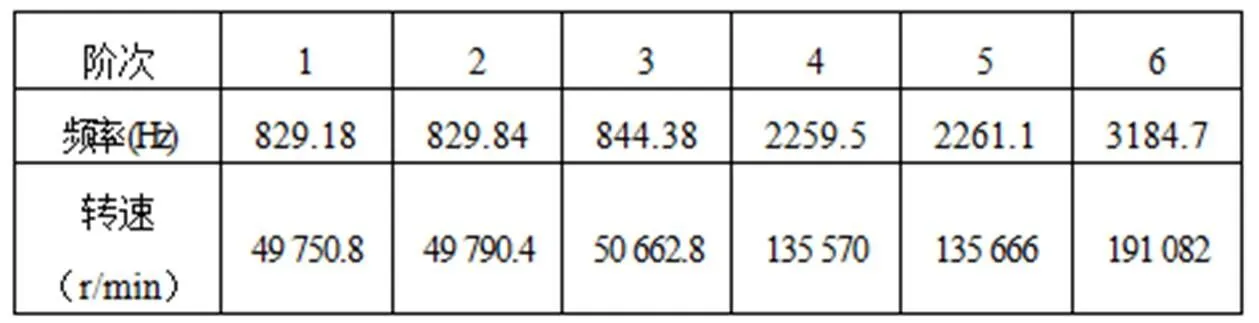
该电主轴的最高工作转速为20 000 r/min，远远低于一阶模态下的临界转速49 750.8 r/min。因此，所研究的精密磨削加工中心的电主轴的结构是合理的，能够有效的避免共振区域，满足使用要求。

5 谐响应分析

当主轴系统所受激振力的频率与主轴的固有频率相同时，电主轴会产生共振，所以必须对电主轴进行谐响应分析。基于前文的模态分析，采用模态叠加法对该高速陶瓷电主轴进行谐响应分析。

5.1 整体位移-频率曲线分析

该高速陶瓷电主轴前六阶模态所对应的频率范围为829.18 Hz~3 184.7 Hz，所以取激振力的频率范围为0 Hz~3500 Hz，设置载荷步数为250步。再分别取电主轴前端、中部以及后端的三个节点进行分析，三个节点分别为175号、25 268号以及44 650号节点，对应的位移-频率曲线如图9所示，其中UX_2为主轴前端变形曲线，UX_3为主轴中部变形曲线，UX_4为主轴后端变形曲线。

图9 主轴前端、中部和后端的径向位移-频率曲线图

从图9可以看出，在0~3 500 Hz范围内，该处的位移有一个脉冲式的突然增大，此时主轴的刚度也随之下降，发生共振现象，所以电主轴在高速运转时应避免这一频率。图中位移-频率曲线变化规律符合实际情况。

5.2 一阶模态固有频率分析

为了保证电主轴运转过程中的正常工作状态，避免出现共振现象，需要对最关键的一阶模态的频率进行局部精确分析，以检验其位移变化情况是否会影响加工。为了提高分析的精度，局部频率范围取为800Hz~900Hz，载荷步为100步，同样对比分析该电主轴前端、中部和后端三处在=829.18 Hz时的位移-频率变化曲线。

对于电主轴前端，取175号节点进行分析，其径向位移-频率变化曲线如图10所示。图中可以看出激振力频率达到主轴一阶模态固有频率时，位移变化增大，发生共振现象。计算可得该电主轴刚度所允许的最大位移量为5 μm，而图中最大位移量远小于5 μm，刚度满足设计所要求的300 N/μm。

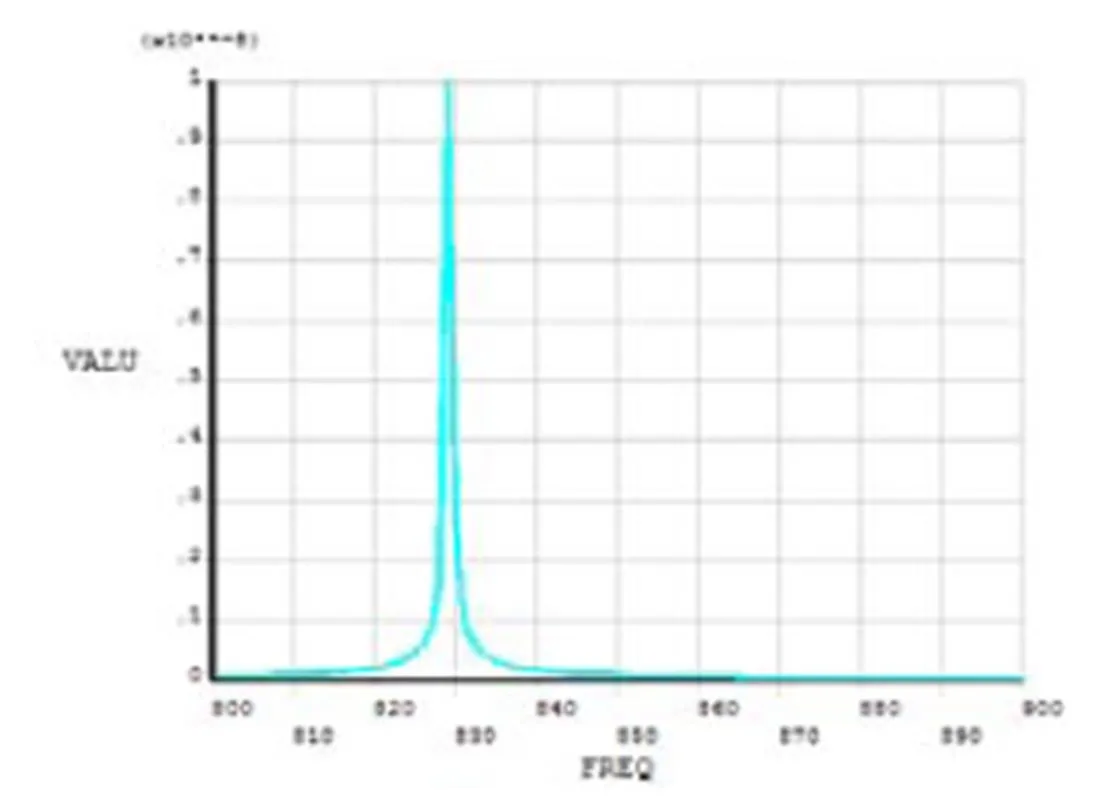
图10 主轴前端径向位移-频率曲线图

对于电主轴中部，取25 268号节点进行分析，因为在模态分析时该处应力值最大，其径向位移-频率变化曲线如图11所示。图中可以看出当激振力频率达到主轴一阶模态固有频率时，位移变化增大，发生共振现象。同时，其最大位移约为0.43 μm，计算此时电主轴刚度为3 555.8 N/μm，满足高速电主轴刚度一般所要求的300 N/μm。

对于电主轴后端，取44 650号节点进行分析，其径向位移-频率变化曲线如图12所示。图中可以看出激振力频率达到主轴一阶模态固有频率时，位移变化增大，发生共振现象。该电主轴刚度所允许的最大位移量为5 μm，而图中最大位移量远小于5 μm，刚度满足设计所要求的300 N/μm。

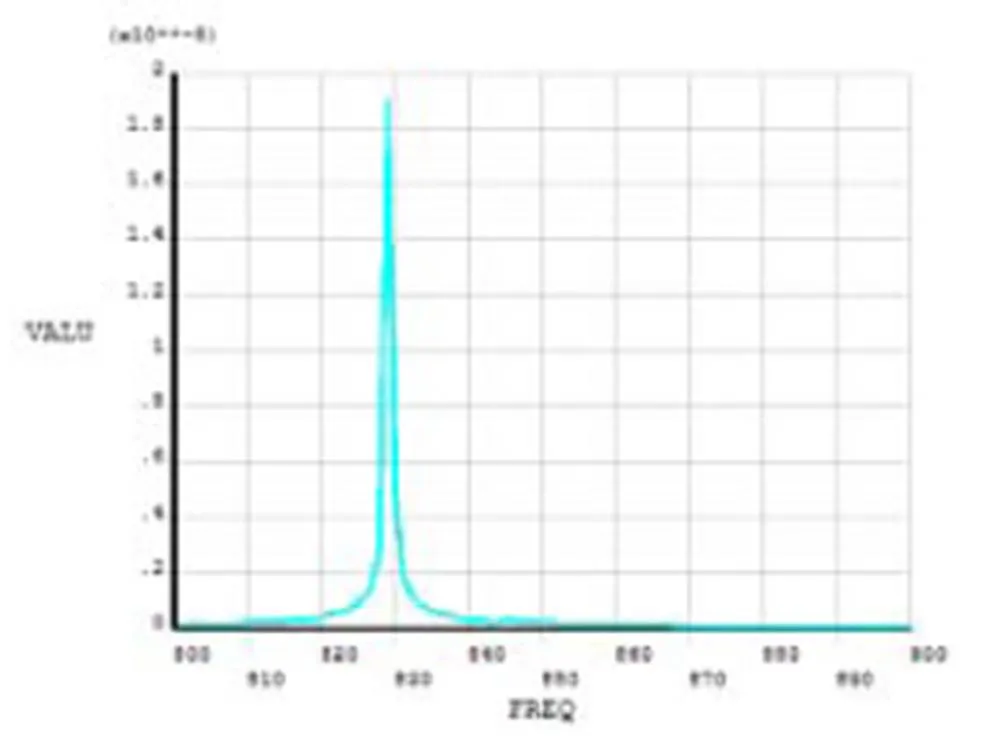
图12 主轴后端径向位移-频率曲线图

综上所述，可以看出，电主轴中部转子在频率达到829.18 Hz时，该处出现最大位移，为危险点，易产生裂纹。频率在800 Hz~900 Hz范围内，主轴前端、中部和后端的径向位移-频率变化曲线对比如图13所示，其中UX_2为主轴前端变形曲线，UX_3为主轴中部变形曲线，UX_4为主轴后端变形曲线。

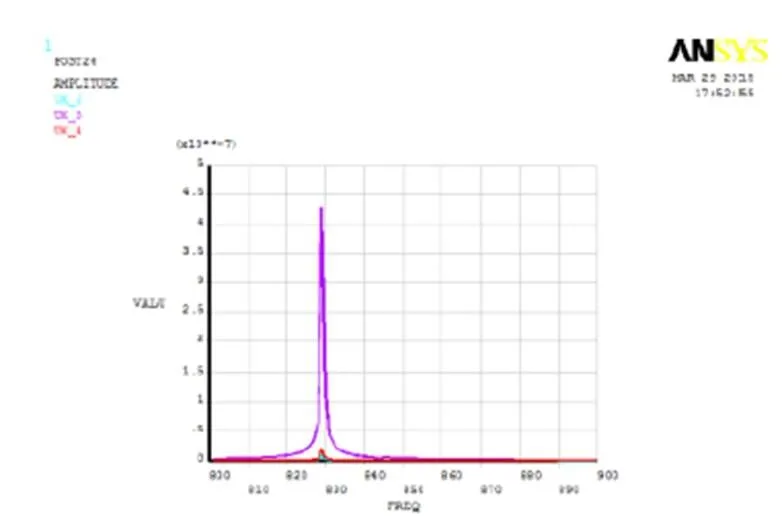
图13 主轴前端、中部和后端的径向位移-频率曲线图

5.3 工作频率分析

由于本文高速电主轴最高转速为20 000 r/min，正常工作状态下均为低频工作，一般不会达到829.18 Hz的工作频率，主要工作频率集中在0~350 Hz，所以需要检验电主轴在低频状态下的位移量及变形情况。

为保证分析的精度，取激振力频率为0~350 Hz，子步数为100，同样选取电主轴的前端、中部和后端三个部位的节点进行比较，其位移-频率变化曲线对比如图14所示，其中UX_2为主轴前端变形曲线，UX_3为主轴中部变形曲线，UX_4为主轴后端变形曲线。可以看出在低频工作范围内，电主轴中部的转子部分的变形量最大，但其最大位移远远小于5 μm，刚度满足使用要求。

图14 主轴前端、中部和后端的径向位移-频率曲线图

6 结语

通过分析某精密磨削加工中心电主轴的基本结构，重点讨论了轴承材料、配置形式及预紧方式的选择过程，最终完成高速陶瓷电主轴基本结构的设计，并对其进行相关的静动态特性分析，分析结果如下：

（2）通过模态分析获得了前六阶模态的固有频率和临界转速，其中一阶模态的固有频率为829.18 Hz、临界转速为49 750.8 r/min，远远大于该电主轴的最高转速20 000 r/min；

（3）谐响应分析获得了该电主轴的不同位置在一定激振力下随频率变化的位移响应曲线，其中在一阶固有频率829.18 Hz附近的最大位移量发生在主轴前端，大小为0.43 μm，远小于该电主轴刚度所允许的最大位移量5 μm，满足使用要求。

[1] ABELE E,ALTINTAS Y,BRECHER C. Machine tool spindle units[J].CIRP Annals-Manufacturing Techno logy,2010,59(2):1-22.

[2] 徐化文.电主轴单元结构及静动态性能的研究[D].兰州:兰州理工大学,2010.

[3] 张海杰.轴承对高速电主轴静动刚度影响的研究[D].兰州:兰州理工大学,2011.

[4] 汪维康,彭阳阳.基于ANSYS的陶瓷电主轴振动模态分析[J].电子测试,2013,08:136-138.

[5] 解文志.高速电主轴动静态特性的有限元分析[D].哈尔滨:哈尔滨工业大学,2006.

[6] 文怀心,夏田.数控机床系统设计[M].北京:化学工业出版社,2005.5,97-103.

[7] 彭文生,李志明,黄华粱.机械设计[M].北京:高等教育出版社,2008.

[8] 崔康.高速电主轴的结构设计与性能研究[D].西安:陕西科技大学,2013.

[9] 王保民,胡赤兵,邬再新等.预紧对高速角接触球轴承动态刚度的影响[J].兰州理工大学学报,2009,02:29-32.

[10] 刘艳华,李志远,张朝煌等.高速角接触球轴承动态刚度的分析与计算[J].轴承,2005,09:1-3.

[11] 王玉丹.转子动力学基础理论及其在电主轴动力特性分析中的应用[D].武汉:武汉汽车工业大学,2000.

[12] 刘道钱,陈涛,沈顺成等.数控铣床主轴部件动态特性分析[J].机械设计与制造,2008,04:172-174.