车用液压减震器外特性仿真

魏文鹏 王姝宁 王天任 闻邦椿



车用液压减震器外特性仿真

魏文鹏 王姝宁 王天任 闻邦椿

（东北大学机械工程与自动化学院 沈阳110819）

针对某车用液压减震器的物理结构及其工作原理，做出合理的模型假设，建立了液压减震器的阻尼特性数学模型。该模型将减震器油液流动情况分为活塞阀系、底阀阀系和储油腔三部分讨论，并且考虑了减震器工作过程中的油液泄露以及储油腔内的气体压力。采用Matlab软件对液压减震器的阻尼特性模型进行仿真，将仿真结果与试验结果对比，发现仿真数据与试验数据之间的误差不超过10%。由此可以得出，建立的减震器阻尼特性模型是准确可信的，该模型可以为减震器外特性设计提供直接参考。

减震器 阻尼特性 仿真 试验

目前，汽车悬架中广泛采用双筒式液压减震器来提供悬架阻尼，减震器的特性对整车的操纵稳定性、行驶平顺性和乘坐安全性都有重要影响。传统的减震器设计方法依靠经验来确定各个参数，然后通过实验对各个参数进行修正，对于不同要求的减震器，需要反复修改参数与进行实验，导致减震器的生产周期长、成本高，而且精度也常常得不到保证[1]。因此，采用仿真软件对减震器的性能进行预测，在设计阶段即能对减震器的性能进行优化成为了重要的研究方向。

在减震器建模仿真研究中，前人建立了各种各样的仿真模型：1970年代Lang建立了包含83个参数的模型，利用模拟电路对减振器的特性进行仿真分析[2,3]；1999年，美国Tenneco汽车部件集团Herr等人采用FEM和CFD相结合的方法分析了减振器阀系的节流特性[4,5]；Duym等人建立了减振器各腔室之间油液流动的模型，对减振器速度特性的滞后性做了专门的研究[6,7]；重庆大学的徐中明根据环形薄板阀片变形微分方程以及内外径处的边界条件，建立了较全面的双筒式液压减振器的数学模型，并用Matlab软件对所建立的模型进行仿真分析[8,9]；武汉理工大学的冯雪梅利用Ansys有限元分析软件对汽车减振器建模，基于稳态分析条件下对所建立的二维模型进行简化[10]等等。这些模型各有优缺点，也有各自的适用范围。其归纳起来即为三种模型：物理参数模型、等效参数模型和非参数模型[11]。

本文在上述模型理论的基础之上，考虑活塞与工作缸之间的油液泄露以及储油腔内的充气压力的影响，建立了减震器的阻尼特性数学模型，并利用Matlab软件，对减震器的阻尼特性模型施加正弦激励进行仿真。仿真结果与实验数据吻合良好，证明本文中所提出的减震器阻尼特性模型是合理可靠的。

1 减震器阻尼特性分析

1.1 减震器的结构

如图1为液压减震器的结构示意图。上吊耳与车身相连接，下吊耳与车轮相连接；工作缸被活塞分为上腔和下腔，活塞杆分别与上吊耳和活塞相连；活塞与底阀座上有不同的阀系结构。当车身与车轮相对运动时，活塞杆带动活塞相对于工作缸运动，工作缸与储油缸内的油液则通过阀系相应流动，产生阻尼力，从而减缓车身与车轮的相对运动，达到减震的作用。

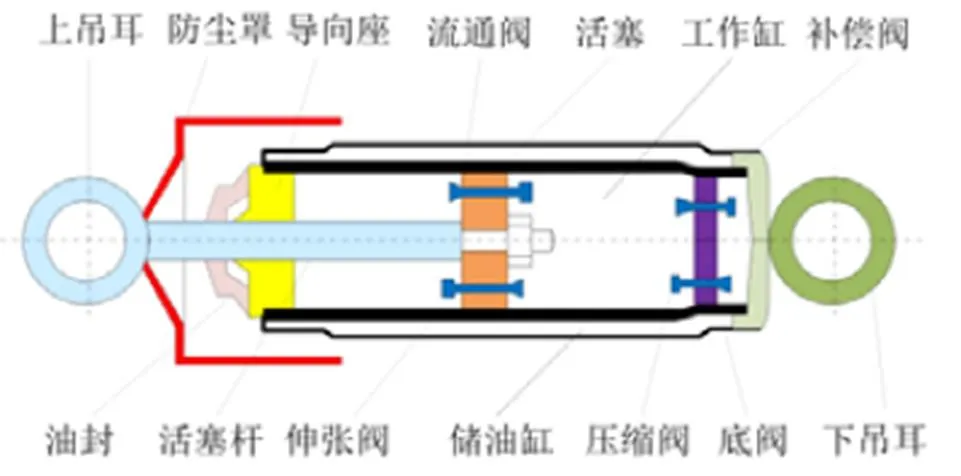
图1 液压减震器的结构示意图

1.2 阻尼力的数学模型

减震器的阻尼特性主要由复原行程和压缩行程决定，复原行程与压缩行程的工作原理类似，以下以复原行程为例讨论减震器的阻尼特性。

根据减震器的工作原理以及其物理结构，以活塞为分析对象进行受力分析，可以得到减震器阻尼力的数学模型如下：

1.3 活塞阀系

活塞总成在复原阀开阀前，由于上腔油液的压力较小，不足以克服复原阀的预紧力，油液只经过活塞上的复原阀常通孔而流入下腔。随着活塞杆继续向上运动，上腔油液压力逐渐增大，将复原阀打开，开阀后油液流经常通孔和复原阀而流入下腔。由于复原阀常通孔的孔长与孔径之比约为2.5，由流体力学知识可知，油液在常通孔中的流动属于管嘴流动；开阀后油液流经复原阀形成圆环平面缝隙流动。所以有：

不管复原阀是否开启，活塞与工作缸之间的缝隙泄露一直存在。油液流经活塞缝隙的泄露属于环形偏心缝隙。由于活塞速度不大，取偏心率=1，则泄漏量可表示为：

1.4 底阀阀系

当活塞杆向上运动，下腔体积逐渐增大，则储油腔的油液会通过底阀阀系流向下腔。此时压缩阀不开启，只能通过常通孔从储油腔流向下腔，压缩阀常通孔的流动形式也是管嘴流动；补偿阀阀片刚度很小，且没有预紧力，当储油腔与下腔的压差很小时补偿阀即会完全打开，其流动形式是圆环平面流动。所以根据流体力学理论有：

复原行程活塞杆向上运动，活塞杆在上腔所占的体积减少，从储油腔流入下腔的油液流量就等于活塞杆体积减少的部分，其表达式为：

1.5 储油腔

式中：为活塞的位移，它随时间变化，与速度之间是导数关系。

综合以上各式可以得到阻尼力与速度之间的关系，即可得到减震器的阻尼特性。

2 仿真与试验

2.1 仿真分析流程

在实际应用中，按照上述理论推导来指导生产显然不太现实，企业需要的是在设计过程中即能得出减震器的特性图，进而分析减震器的性能。基于上述需求，利用Matlab软件的GUI界面设计，开发一套求解减震器特性曲线的仿真软件，仿真求解流程如图2所示。仿真过程中所用的主要参数如表1所示。

图2 液压减震器阻尼特性仿真流程图

表1 仿真过程主要参数

2.2 仿真分析与实验结果对比

根据我国减震器台架试验标准JB3901-85规定，对减震器施加正弦激励

则活塞与工作缸的相对运动速度为

结合上述减震器的数学模型，得到了减震器的阻尼特性曲线如下图所示。图3为减震器的速度特性图，图4为减震器的示意图。

图4 减震器示意图

表2 仿真数据与试验数据对比

根据仿真所得的减震器阻尼力与试验所得阻尼力值比较，其误差不超过10%，即仿真模型所得出的结果与实际试验结果吻合良好，从图3中可以看出在本文所用参数下，减震器的开阀速度约为 0.12 m/s。

3 结语

根据减震器的实际结构以及做出的合理假设，建立了减震器外特性即速度特性和示功特性的计算模型，由模型仿真得出的外特性数据与厂家提供的实测数据的误差不超过10%，仿真特性与实际特性良好吻合，证明本文建立的减震器阻尼特性模型是合理正确的。

[1] 任卫群,赵峰,张杰.汽车减震器阻尼特性的仿真分析[J].系统仿真学报,2006,18(Suppl.2):957-960.

[2] Lang H.H. A Study of the Characteristics of Auto motive Hydraulic Dampers at High Stroking Frequencies[J].University Mivhigan.1977,(1):256-327.

[3] L.Segel. H.H.Lang. The Mechanics of Automobile Hydraulic Dampers at High Stroking Frequencies [J]. Vehicle System Dynamies.1981(10):568-593.

[4] Herr F,Mallin T,Lane J,et al.A shock absorber model using cfd analysis and Easy[J].1999(11):13-22.

[5] C.Surace,K.Worden.An Improved Nonlinear Model for an Automotive Shock Absorber[J]. Nonlinear,Dynamics,1992(3):413-429.

[6] Stefaan.W.Duym, Randy Stiens. Physical Modeling of the Hysteretic Behavior of Automotive Shock Absorbers[J].SAE Paper ,1997(1):46-51.

[7] Lee K. Numerical Modeling for the HydraulicPerformances Prediction of Automotive Mon tube Dampers[J].Vehicle Sysdyna,1997(28):25-39.

[8] 徐中明,李仕生.汽车减振器外特性仿真与试验分析[J].振动与冲击,2011,30(8):92-96．

[9] 徐中明,李仕生.基于Matlab/Simulink的汽车减振器外特性仿真与性能分析[J].汽车工程,2011, 33(4):329-334.

[10] 冯雪梅,刘佐民,魏东.减振器双节流孔闭式油路稳态行为特征有限元分析[J].机械设计与研究.2003,19(1):66-69.

[11] 李世民,吕振华.汽车筒式液阻减振器技术的发展[J].汽车技术,2001(8):10-16.