基于Deform 3D对磨削表面残余应力的仿真研究

贾亚凯 李 静 沈南燕 何永义



基于Deform 3D对磨削表面残余应力的仿真研究

贾亚凯 李 静 沈南燕 何永义

（上海大学 上海大学机械自动化及机器人重点实验室 200072）

针对钛合金材料磨削加工难的特点，利用有限元软件Deform 3D通过建立能够反映材料在磨削过程中表现出的大应变、高温及高应变率的Johnson-Cook材料本构模型来模拟钛合金TC4的磨削加工过程，并对磨削后工件所受的残余应力进行了分析。验证了有限元模型的有效性和正确性，为完善钛合金残余应力的研究以及工艺参数的优化选择指明了方向。

钛合金 表面残余应力 Deform3D

钛合金是典型的难加工材料。其磨削加工难点表现如下:（1）砂轮粘附严重，粘附物脱落将导致砂轮磨粒的破碎与脱落；（2）磨削过程中变形复杂, 生成层叠状挤裂切屑；（3）磨削力大、磨削温度高；（4）化学活性强，容易与空气中的氧气发生化学反应释放出大量的热量，使得磨粒表层逐层剥蚀，最终导致砂轮氧化磨损。

钛合金的应用领域以及磨削加工的高精度决定了其运用磨削加工的必要性。因钛合金应用领域之广泛，对其加工表面质量的研究尤为重要，而加工后表面残余应力对工件的使用性能影响极大是表面质量评价的主要指标之一。

但在实际加工过程中的表面残余应力、应变、温度等的测量及其困难，仅通过实验无法对磨削机理进行深入的研究，而且也不切实际。

利用有限元分析技术分析对磨削过程进行仿真分析不仅能对机理进行深入研究，并可方便地对磨削加工工艺进行优化，同时还能节约加工成本降低加工中带来的安全隐患。

利用软件Deform 3D，对难加工材料钛合金(TC4)进行高速磨削（砂轮速度在45~94 m/s之间）工艺仿真。

分析不同磨削参数下（砂轮速度、工件速度和磨削深度）磨削加工后表面残余应力的分布规律。同时将仿真结果和实际试验结果进行对比分析，阐述高速外圆磨削的表面残余应力与加工参数之间的关系，从而为钛合金磨削工艺参数的优化选择提供指导。

1 有限元模拟的理论基础

1.1 材料本构模型的建立

在外圆磨削过程中，难加工材料钛合金（TC4）处于高温、大应变和高应变率的情况并会发生热弹塑性变形，因此构建能够反映材料特点的材料本构模型是仿真结果的正确性和可靠性的基础和前提。选用Johnson-Cook(J-C)材料本构模型[1]描述工件材料最为合适。J-C材料模型是一个能反应应变率强化效应和温升软化效应的理想刚塑性强化模型，该模型利用变量乘积关系分别描述应变、应变率和温度的影响。该模型具体表达式如下：

1.2 模型的简化和假设

磨削加工的本质仍然是磨粒的切削作用[2]，而且实际参加磨削的磨粒数甚少，因此可以将整个砂轮简化为单颗磨粒，如图1所示，使仿真过程得以简化。

单颗磨粒以一定的速度和工件发生相互作用，在磨削区发生了复杂的物理化学变化，同时工件也会产生相应的塑性变形。

(a)

(b)

图1 单颗磨粒三维图及磨粒磨削工件的二维模型

2 仿真模型的建立与求解

2.1 几何模型的建立

在SolidWorks中画出单颗磨粒的砂轮及工件的三维实体图，保存成.stl文件形式输出，在Deform 3D前处理中导入三维几何模型，其中Top-Die为砂轮，设置成刚性（rigid）；Workpiece为工件，设置为塑性（plastic）。为了方便进行工件的预处理设置以及提高求解速度，在本研究中，取工件的1/18作为研究对象。

2.2 预处理设置

预处理设置作为加工仿真分析的准备工作，主要完成前处理设置、生成数据库和模拟运算三个步骤[3]。在仿真控制（Simulation Control）中设置仿真步数为1 000步，时间增量为1x10-6s，存储增量为每25步保存一次，时间步长不能太大，否则会降低求解精度，导致网格严重畸变甚至不收敛。采用国际单位标准SI，仿真模式为热传递（Heat Transfer）和变形（Deformation）；迭代方法（Iteration Method）采用Direct iteration；求解器（Deformation Solver）采用共轭梯度法（Conjugate0Gradient Solver）。采用四节点四面体对工件进行网格划分，砂轮和工件均采用绝对类型，砂轮网格数2.5万，转动中心（0,0,0）；工件网格数为10万，材料为TC4，工件的热导率如表1所示[4]。

表1 工件的热导率

3 仿真结果分析

3.1 磨削区应力分布

3.1.1 等效应力场（stress-effective）的分析

从图2中可以看出，不论磨削用量如何变化，等效应力场的分布规律都是一致的。在磨削区内，应力场曲线基本上是平行的，均匀的，并向两边逐渐减小，这是由于温度梯度对材料的软化作用；随着磨削深度的增加，表面变形加剧。

（a）s= 45m/s，v= 40r/min，a=1 µm

(b) v=45 m/s，v=40 r/min，a=2 µm

(c)vs=45 m/s，vw=40 r/min，ap=3 µm

图2 等效应力场分布云图和等值线图

3.12 最大主应力(stress 一maximum principal)的分析

图3为磨削区最大主应力分布曲线。由图3中可以看出，在磨粒前侧、靠近磨粒尖端处为压应力，最大压应力为-3 430 MPa；在磨粒后侧为拉伸应力区，最大拉应力为3 900 MPa；在刃口区明显存在着应力分流点，磨粒-工件接触区受压应力作用，磨粒后区受拉应力作用。

（a）

(b)

图3 最大主应力分布云图和等值线图

3.1.3 磨削方向上的应力

在图4中，应力等值线E相当于磨粒后侧的延长线，可以看出：从磨粒刃口区开始至磨粒前侧，E线之下全部受压应力作用，最大压应力在磨粒尖端处，为-4 280 MPa，说明磨粒尖端出现应力集中，这就是实际加工中将刀尖做成圆弧过渡的原因。在E线以上磨粒与工件接触的上半部分（接近工件表层）受到拉伸应力作用，最表层拉应力值为552 MPa，里层受到的拉应力值为3 450MPa。

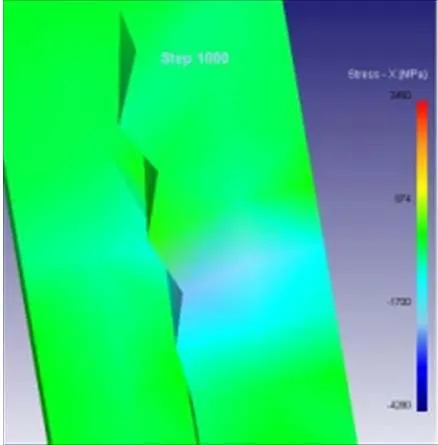
(a)

（b）

图4 磨削方向上的应力场

通过以上分析可知，在磨削过程中剪切区的等效应力和变形最大，刀屑接触区次之，磨粒-工件接触区的应力场最小。剪切区的应力场中的应力分布均匀并且有延伸到磨粒后侧的趋势，这对第三变形区会产生直接影响。此外，磨削方向的应力是磨削过程中工件表面所受的主要应力，以及拉压残余应力的分界线在分流点处，工件表面基本受残余拉应力作用而垂直于磨削方向上的残余应力因其数值太小可以忽略。

3.2 磨削速度对表面残余应力的影响

这里的磨削速度是砂轮速度和工件速度的合成速度（其中砂轮速度占主导地位）在磨削过程中，金属的变形只发生在磨削平面，即X-Y平面。已加工表面残余应力以磨削方向残余应力为主，而垂直于磨削方向残余应力只是磨削方向残余应力的产生结果。本文对砂轮速度分别为45 m/s、60 m/s和94 m/s，工件速度为200 r/min，磨削深度为3mm进行仿真分析。在此磨削条件下进行磨削过程仿真，通过Deform 3D的后处理模块提取工件表面的残余应力值，并将不同的磨削速度进行对比，得到如图5所示的曲线。

从图5可以看出，当v越大，磨削产生的压应力值越大。这是因为随着磨削深度的增加，工件的热量不易传入里层，最终削弱了热载荷的作用，挤光作用占主导地位，从而表现出压应力状态。当压应力值达到最大值后，又开始减小，变化较平缓，最终应力值趋于零。

这是因为当深度继续增加时，里层的金属受到磨削的影响很小，导致机械应力的作用逐渐减弱。在工程中，由于残余压应力对加工后工件的机械性能有益，结合仿真结果可知，砂轮速度达到一较大值时有利于提高工件的残余应力。

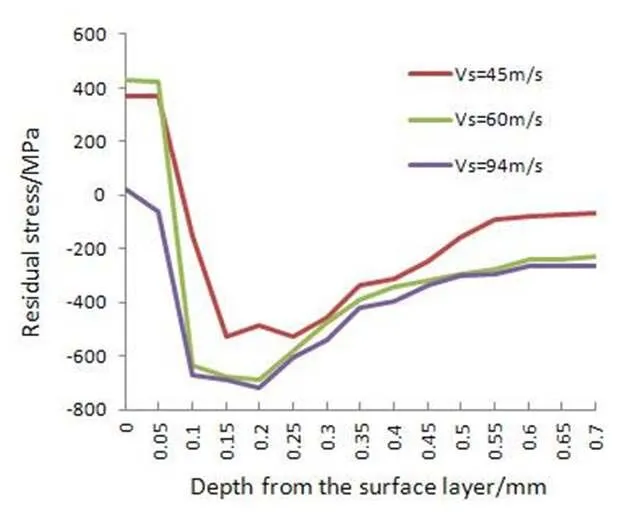
图5 不同砂轮速度对残余应力的影响

3.3 磨削深度对表面残余应力的影响

磨削条件：磨削深度分别为1 mm、2 mm和3 mm，工件速度为200 r/min，砂轮速度为60 m/s。在此磨削条件下进行模拟磨削过程，通过Deform 3D的后处理模块提取工件表面的残余应力值，并将不同的磨削深度进行对比，得到如图6所示的曲线。在次表层中，残余拉应力迅速下降并且转变为压应力，在0.1~0.2 mm处出现压应力峰值，随之逐渐减小。随着磨削深度的增大，残余压应力的峰值增大，并且其位置逐渐向工件内部深入。这是因为在磨削表层热应力占主导地位，而随着距离表层距离的增加塑性变形引起的机械应力逐渐增大，即表现为残余压应力。而当磨削深度增加时，工件塑性变形越明显，表现为残余压应力增大的现象。

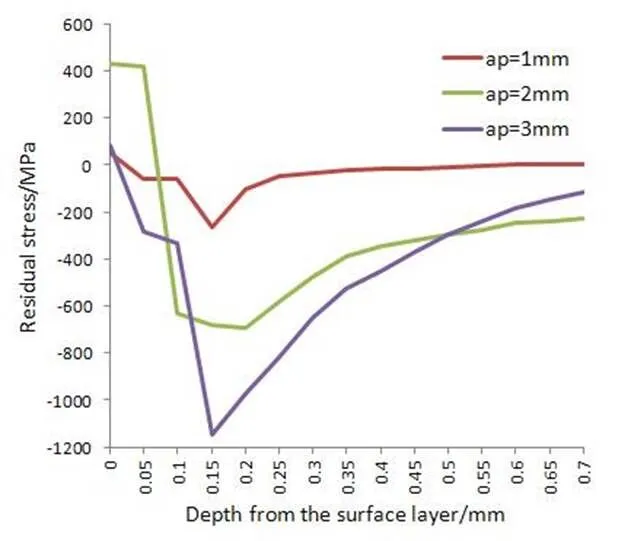
图6 不同磨削深度对残余应力的影响

3.4 仿真结果与试验结果对比分析

磨削加工后工件所受的残余应力不仅影响零件的表面质量，而且影响着零件的尺寸精度、疲劳强度、精度稳定性等性能。高速磨削作为现代先进加工手段之一越来越受到重视，在国内外有关外圆磨削或是高速外圆磨削都取得了很大进展。盛晓敏等[5]在314 m/s的超高速磨床上分析了磨削参数对工件表面温度的影响，验证了高速磨削的有效性。Gong等[6]对超高速磨削中的冷却系统进行了研究和仿真,分析指出砂轮速度和砂轮宽度是磨削区最大动压力的显著影响因素。

试验[7]结果表明：表面残余应力随着砂轮速度v的增大而增大，且砂轮速度对表面残余应力的影响最大；轴向表面残余应力与磨削深度a之间有着单调递增的关系，而周向表面残余应力随着磨削深度a先减小后增大，当磨削深度a取可行范围中间值时，表面残余压应力最小，同时表明磨削深度对表面残余应力的影响弱于砂轮速度对其的影响。

对比仿真结果与试验结果，可知有限元仿真得到的砂轮速度和磨削深度对表面残余应力的影响规律与实验所得规律基本一致，但在数值上有些误差。二者共同表明：砂轮转速v影响最显著并且高速磨削和大的磨削深度更有益于得到综合性能优异的零件。这验证了有限元磨削模型的有效性和准确性。同时有限元仿真方法还对不同深度的表面残余应力分布进行了研究，其分析出的残余应力分布规律为完善残余应力的研究指明了方向。

4 结语

通过对钛合金的磨削过程数值模拟，得出了磨削加工后表面残余应力的分布规律：

(1) 砂轮速度对工件表面残余应力影响最显著，且高速磨削得到的表面质量更好，磨削深度对工件表面残余应力影响较次之，在可行范围内较大的磨削深度有于获得表面残余压应力。

(2)砂轮速度和磨削深度对残余应力场分布深度有直接影响，且随着磨削深度和砂轮速度的增大残余压应力最大值增大。

(3)仿真分析与实验结果在砂轮速度和磨削深度对表面残余应力的影响规律分析方面基本吻合，但数值上有所差异，因为仿真过程中存在着某些简化和假设，与实际情况存在差距。

[1] Johnson G R,Cook W H. Fracture Characteristics of Three Metals Subjected to Various Strain,Strain Rates, Temperatures and Pressures[J].Engineering Fracture Mechanics, 1985,21(1):31-48.

[2] 李伯民,赵波.现代磨削技术［M］．北京:机械工业出版社,2003.

[3] 李传明,王向丽,闫华军.DEFORM5.03金属成型有限元分析实例指导教程[M].北京:机械工业出版社,2007.

[4] 编辑委员会,工程材料实用手册第4卷第2版，北京：中国标准出版社,2001.

[5] 盛晓敏,陈涛,张国华等.超高速磨削工艺对45钢表面磨削温度影响实验研究[J].机械设计与制造,2006,09:177-179.

[6] Gong YD,Li H, zhao, X X, Wang W S. Researches and simulations on hydrodynamic in super high speed grinding area[J].KeyEngineeringMaterials,2006,315-316:541-545

[7] Shen Nanyan,Jia Yakai，Li, Jing. Surface roughness of titanium alloys TA2 and TC4 in high-speed cylindrical grinding[J]. WIT Transactions on Engineering Sciences,Advanced Materials and Information Technology Processing 2014,87:213-220.