抗滑桩设计推力计算的有限元方法

雷 达，蒋关鲁，林展展，张树明，王智猛

(1.西南交通大学土木工程学院，四川成都 610031;2.西南交通大学 道路与铁道工程铁道部开放实验室，四川成都 610031;3.中铁二院工程集团有限责任公司，四川 成都 610031)

抗滑桩加固滑坡已经成为滑坡灾害治理的主流工程措施，它充分利用抗滑桩和桩周岩土体的交互作用，平衡滑坡推力，同时分担部分下滑推力到基岩锚固段。目前，利用传递系数法和相应修正公式进行抗滑桩设计的方法，因其简单实用的力学原理和成熟的工程应用而成为主流方法。潘家铮［1］提出，先计算达到设计安全系数时滑坡断面的下滑推力，再计算自然条件下的下滑推力，差值为抗滑桩设计推力。由于忽略岩土体自身稳定能力，计算结果偏于保守。贺建清等［2］认为抗滑桩在受荷的同时对桩前土体或围岩产生反力，假定桩前抗力传递系数为a，设计推力必须减去桩前抗力，但取值条件有待商榷。和海芳等［3］认为抗滑桩前后滑体拥有相等的安全系数，提出以滑坡剪出口附近滑块推力是否收敛于0为判别条件，确定桩前剩余下滑力，以抗滑桩前后推力差值作为设计标准。王培勇等［4］分别从上往下计算滑坡推力，从下往上计算抗滑力，以两者差值作为抗滑桩设计推力。

以上计算遵守刚体极限平衡假定，滑面满足静力平衡，但不满足力矩平衡。只能进行近似分析，不能真实表现土的弹塑性应力—应变关系，抗滑桩设计推力计算存在一定误差。程建军等［5］研究表明有限元法的滑坡推力计算结果相对合理，应该推广应用。本文结合成兰铁路右所屯滑坡，利用有限元软件FLAC3D模拟滑坡地应力场、位移场、边界条件等，进行非线性分析，并与传递系数法进行比较。

1 有限元法计算原理

主要用到两个本构计算模型:各向同性弹性模型、摩尔—库伦模型［6-7］。低应力水平时使用各向同性弹性模型，认为土体近似产生各向同性弹性变形，根据胡克定律有

式中:K，G分别为体积模量、剪切模量，δij为克罗内克δ函数，Δσij为应力张量增量，Δεij，Δεkk为应变张量增量，应力计算没有残余变形分量。使用摩尔—库伦模型模拟滑坡塑性流动破坏时，弹性变形产生的广义应力增量仍然用胡克定律进行计算。

滑坡破坏是由降雨、地震等工况引起的滑面强度参数的降低，弹性模型不涉及。利用摩尔—库伦模型得到的剩余下滑力应扣除弹性解，即:F剩余下滑力=

2 有限元法算例

2.1 工点概况

右所屯工点位于成兰铁路 D3K247+788—D3K247+846段，滑体轴向长100 m，宽40～60 m，滑体厚3～15 m，为一中型堆积层滑坡，线路从滑坡前缘通过。滑体为粉质黏土，滑带为细角砾土，基岩为以弱风化为主的炭质板岩夹砂岩。根据前期地质调查结果，滑体和滑带之间存在潜在滑动面，在降雨、地震等恶劣工况下，将沿滑面发生整体滑动破坏。为简化计算分析，滑体粉质黏土换为细角砾土，滑坡土层物理参数如表1所示。

表1 滑坡土层物理参数

2.2 建立数值计算模型

监测断面划分如图1所示，共8个，监测断面受力为网格节点合力，滑体和滑带分界面附近存在10 cm厚细角砾土潜在滑动面。根据右所屯工点滑坡主轴断面图，建立单位宽度的有限元计算模型，共有单元体2 542个、节点5 284个。在滑坡模型的X方向两侧边界和Y方向，用fix设置固定节点速度和位移的边界条件，底部边界同理为X，Y，Z三向的速度位移固定约束。

图1 监测截面示意(单位:m)

2.3 剩余下滑力分步计算

计算前，移除监测截面沿滑坡剪出口方向的岩土体。以x=64 m监测截面为例，移除监测截面至左侧边界之间的岩土体，并对x=64 m岩土体边界施加固定节点位移和速度的约束，按照以下三步计算:①利用弹塑性求解法生成初始地应力，鉴于黏聚力为0，对滑面摩擦角进行折减，在摩尔—库伦本构模型下数值计算得到受力稳定后的截面合力F1，运行时步5万步。②利用弹性本构模型生成初始地应力，得到计算截面的弹性合力F3。③由于滑坡失稳的根本原因是摩尔—库伦本构模型中，潜在滑动面的摩擦角变小产生下滑力［8］，而弹性本构模型只涉及体积模量、剪切模量、密度，故在推力中扣除弹性解部分，F1和F3的差值F4为滑面摩擦角折减时监测断面的剩余下滑力。

传递系数法计算公式见式(9)和(10)，为便于和传递系数法的计算结果进行比较，分为4种工况分别计算剩余下滑力，即潜在滑动面内摩擦角分别折减为30°，25°，20°，10°。

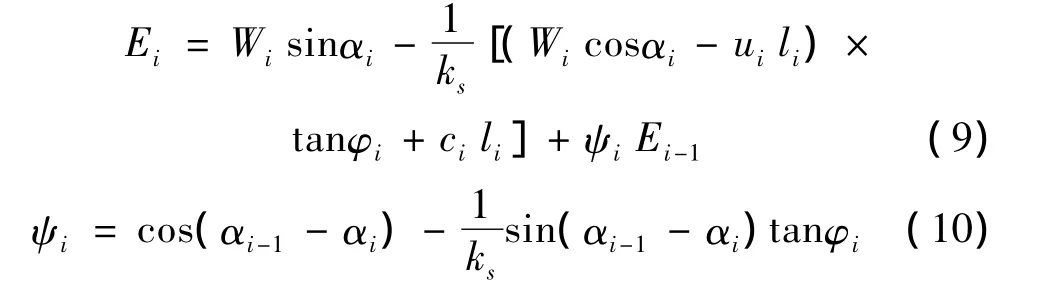
式中:Ei为第i个条块末端的滑坡推力，kN/m;ks为安全系数(视工程重要性、整治难易程度);Wi为第i个条块滑体重力，kN/m;αi－1为第 i－1个条块所在滑动面的倾角，(°);αi，φi，ci，ui，li分别为第 i个条块滑动面的倾角、内摩擦角、单位黏聚力、单位孔隙水压力和长度。

2.4 结果分析

图2为有限元法和传递系数法剩余下滑力对比，为便于分析，剩余下滑力均取X方向(水平方向)分力。传递系数法下滑推力变化的线性特征明显，有限元法曲线变化缓和平稳，能较好地模拟推力的非线性变化。随着滑动面土层摩擦角减小，滑动面摩阻力变小，滑体内部弹塑性作用效果减弱，推力曲线线性特征逐渐明显。当滑动面摩擦角为10°时，两种算法推力曲线的线性特征非常显著。传递系数法在滑面摩擦角大幅折减时，抗滑段下滑推力没有收敛减小趋势，一直传递到最后一个土块;有限元法则能清晰分辨下滑段和抗滑段。当滑动面摩擦角为30°时，传递系数法推力曲线在距离坡脚26 m时已经收敛为0，这与实际工况不符。有限元法则能显示滑坡推力先增加后减小的规律，没有截面推力突变为0的情况。由于两种算法的理论基础不同，传递系数法的推力峰值大于有限元法，曲线变化规律一致，下滑力峰值都出现在X方向88 m处。

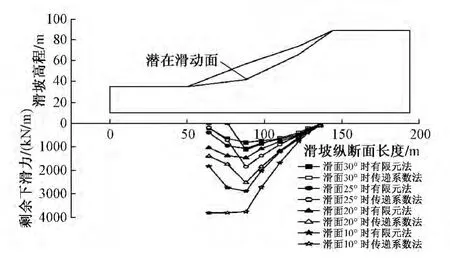
图2 剩余下滑力对比

图3 剩余下滑力增量对比

图3为滑动面摩擦角变化时的剩余下滑力增量对比。当滑动面摩擦角变化区间为30°～25°，25°～20°时，两种方法的剩余下滑力增量变化趋势一致，且传递系数法增量均大于有限元法，说明传递系数法对剩余下滑力增量有放大效应，这种方法对工程设计偏于安全。随着滑动面摩擦角折减加剧，理论上25°～20°区间的剩余下滑力增量应大于30°～25°时的，但传递系数法下滑段的5个监测截面不满足此规律。当滑动面摩擦角变化区间为20°～10°时，抗滑力急剧减少导致滑体产生剧烈位移，两种方法的增量变化在下滑段相近。但在抗滑段表现出不同的趋势，传递系数法的下滑力增量不断增加，没有收敛趋势。

2.5 设计推力计算

自然状态时储备的抗滑力使滑体处于稳定状态。随着滑面摩擦角不断减小，当滑坡处于极限破坏平衡状态时，临界摩擦角出现，抗滑力已发挥全部作用，监测截面的剩余下滑力和抗滑力平衡。有限元法利用FISH程序语言编写LOOP循环语句［9］，对滑面摩擦角进行折减试算。以程序内置力不平衡比率＞1×10－5为终止标准，得到滑面临界摩擦角为27.63°，安全系数为1.338，计算显示滑坡上部表层发生溜塌。传递系数法按照式(9)和式(10)试算，直到滑坡剪出口附近滑块推力近似为0，得到滑面临界摩擦角为24.85°，安全系数为1.512。

以滑面摩擦角20°时为基准，比较抗滑桩设计推力。有限元法按照剩余下滑力的计算步骤，得到临界极限状态和基准条件时的剩余下滑力，两者差值即为抗滑桩设计推力。

2.6 结果分析

图4显示两种算法的设计推力曲线有一致的变化规律，但传递系数法各点设计推力均大于有限元法，这种差异在抗滑段达到最大。

图4 设计推力曲线

3 结论

1)和传递系数法相比，利用有限元法模拟塑性流动和破坏，曲线变化相对平缓，能缩小剩余下滑力的计算误差，不会出现抗滑段剩余下滑力计算不收敛或提前收敛于0的情况。

2)有限元法的设计推力变化趋势与传递系数法一致，且小于传递系数法的计算结果。

［1］潘家铮.建筑物的抗滑稳定和滑坡分析［M］.北京:水利出版社，1980:155-184.

［2］贺建清，张家生，梅松华.弹性抗滑桩设计中几个问题的探讨［J］.岩石力学与工程学报，1999，18(5):600-602.

［3］和海芳，祁生文，伍法权，等.抗滑桩设计推力计算方法研究［J］.工程地质学报，2008，16(5):694-698.

［4］王培勇，刘元雪，冉仕平，等.基于传递系数法确定支护桩设计推力的新方法［J］.四川大学学报(工程科学版)，2010，42(6):73-78.

［5］程建军，廖小平，王浩，等.滑坡推力计算方法的对比研究与应用［J］.水文地质工程地质，2008(1):44-47.

［6］陈育民，徐鼎平.FLAC/FLAC3D基础与工程实例［M］.北京:中国水利水电出版社，2009.

［7］Itasca Consulting Group，Inc..Fast Language Analysis of Continua in 3 Dimensions，Version 3.0，User's Manual［M］.Itasca Consulting Group，Inc.，2005.

［8］DAWSON E M，ROTH W H，DRCSCHER A.Slope Stability Analysis by Strength Reduction［J］.Geotechnique，1999，49(6):835-840.

［9］彭文斌.FLAC3D实用教程［M］.北京:机械工业出版社，2008.