柱面QR 码的识别及实现

刘烽杰，蔡 明

(江南大学物联网工程学院，江苏 无锡 214122)

0 引言

QR 码又称快速响应矩阵码，是一种最常用的二维码。如今，扫码软件通过智能手机自带的摄像头便可轻松扫出QR 码信息，但这仅限于平面上的QR码。当条码被粘贴或打印在圆柱面上时，由于无法检测到探测图形，识别困难。

本文的研究背景是实现校园的自主导游，QR 码粘贴于白色柱面上，背景相对清晰。平面QR 码的校正首先是获取到3 个位置探测图形，然后根据坐标判断旋转角度来确定方位。柱面QR 码在三维空间产生了畸变，导致无法准确定位探测图形，因此采用传统识别方法行不通。文献［1］利用探测图形的特征进行定位，接着利用逐像素映射还原算法重构QR码，但必须保证获得的初始图像为正投影图像，且三维空间的畸变程度不能太大。文献［2］利用探测图形具有相同的重心来定位，虽然在畸变较大的场合下仍适用，但也必须满足正投影的要求。而在实际扫描时，图像往往在二维空间也产生了畸变，因而很难满足正投影的要求。

考虑到此刻柱面QR 码环境的特殊性(背景清晰)，根据几何学中辅助线的理念(即辅助线是在原图基础上所作的具有极大价值的直线或线段)，提出了在QR 码外部加一个平行于4 条轮廓的黑色辅助矩形，利用它进行平面的校正。接着利用定位图形重心相同的特征获取到定位图形坐标，再应用直线最佳逼近法获取4 条轮廓。之后进行区域分割还原进行三维图像的校正，形成标准的QR 码图像。

1 二维空间校正及条码定位

QR 码是由深浅正方形模块组成的一个正方形阵列，主要包括功能区域和编码区域［3］。功能区域由探测图形、分隔符、定位图形和校正图形等组成。其中位置探测图形位于3 个边角，用于快速定位QR码在原图中的位置。

如图1 所示，L 为一根水平穿过平面探测图形和柱面探测图形的直线。其中，平面探测图形从左往右具有固定的比例1∶1∶3∶1∶1。由QR 码的编码规则可知，出现如探测图形特征的区域基本不可能［3］，因此通过查找类似比例的区域来确定探测图形是可行的。传统的识别算法一般是在获取到探测图形的基础上，利用Hough 变换将图像旋转至水平，再用双线性变换和双线性插值算法校正几何形变。在此基础上经傅立叶滤波得到比较精确的条码模块，最后提取码字信息［4］。对圆柱面而言，畸变程度不大时，该比例尚明显。当畸变程度较大时，从图1 可以看出，比例发生了改变，导致通过获取探测图形来识别QR 码的方案行不通，再加上二维平面上的畸变，使得柱面QR 码的识别更加不易。为了准确识别，必须先将畸变的QR 码进行平面的校正，在这基础上，才能再次进行三维空间的校正。经过思考，可以通过添加辅助矩形来达到这一目的。

图1 平面及柱面定位图形比较

1.1 二维几何校正

对添加了辅助矩形的QR 码(见图2)校正，具体步骤如下［5］:1)利用Hough 变换提取出该矩形，求得4 个顶点坐标。因为Hough 变换不仅可以用于直线的提取，对于曲线同样适用［6］。2)对图像做几何运算校正失真，并旋转至水平。在做几何运算时，首先进行空间变换，描述每个像素如何从初始位置转换至终止位置，同时还要进行灰度级插值，因为在一般情况下，输入图像的位置坐标为整数，经过运算，输出图像的坐标往往为非整数。因此，这里采用双线性插值算法，即对每一个目标像素设置坐标，通过反向变换来得到浮点坐标(i +u，j +v)。其中i，j 均为非负整数;u，v 为［0，1)区间的浮点数。设这个像素的值为f(i+u，j+v)，则该值可由原图像中坐标为(i，j)、(i+1，j)、(i，j+1)、(i+1，j +1)所对应的周围4 个像素的值决定，即:

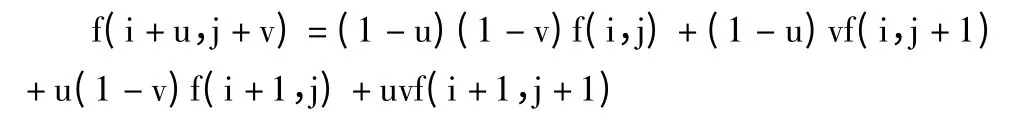
其中f(i，j)表示原图像(i，j)处的像素值。以此类推，得到平面校正后的图像(见图3)，即正投影图像。

图2 添加辅助矩形的QR 码

图3 平面校正后的QR 码

1.2 定位图形定位

在利用辅助矩形实现了柱面QR 码的平面校正后，得到的相当于正投影的图像。此刻，如果畸变程度比较大，采用符号特征定位显然不行。从图3 可以看出，在扫描后，3 个探测图形具有很明显的特征，即重心相同。因此，抓住这一点来确定探测图形的坐标。探测图形的重心可以通过式(1)计算得出［7］:

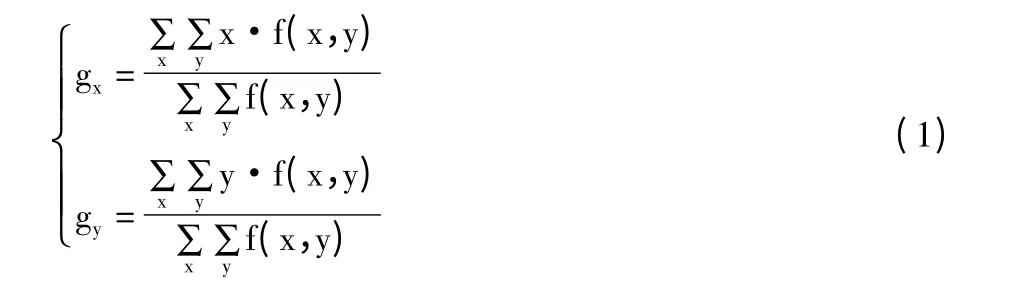
式中:gx和gy分别代表重心点的x，y 坐标;f(x，y)是(x，y)点处的灰度值。在轮廓图像中取逻辑值0 或1，式(1)可以简化为:

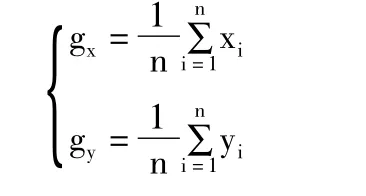
1.3 条码边界提取

QR 码与其他条码不同的是它不存在起始符和终止符，因此要直接扫描得到条码边界是不可能的。多数文献中采用Hough 变换来提取，但无论是应用于整幅图案还是隔行应用，都是比较浪费CPU 资源的。本文在已知定位图形坐标的基础上，采用直线最佳逼近法获取条码的轮廓［8］，如图4 所示，具体算法如下:

1)设1.2 节中所获得的3 个定位图形的重心分别为P1，P2，P3。过任意2 点作直线，共得到3 条直线(图中直线P1P2，P1P3和P2P3)。

2)使3 条直线分别向远离另一个点的方向移动(如图中P1P2向上移动，箭头代表移动方向)，每次偏移2 个像素，求出各条直线扫描图像得到的波形。根据扫描线所得波形进行对比、判断。在到达边界时来回扫描，微调直线斜率，得到最佳逼近直线。

3)移动过程中，由于直线P2P3无法得到最佳逼近效果而被抛弃，因此获得PAPB和PAPC两条直线。接着分别作过点P2平行于P1P3的直线和过点P3平行于P1P2的直线，使直线向箭头标识方向进行扫描，从而得到另外2 条边界直线。图中PAPB，PAPC，PCPD，PBPD这4 根直线即为QR 码轮廓，PA，PB，PC，PD为4 个顶点。

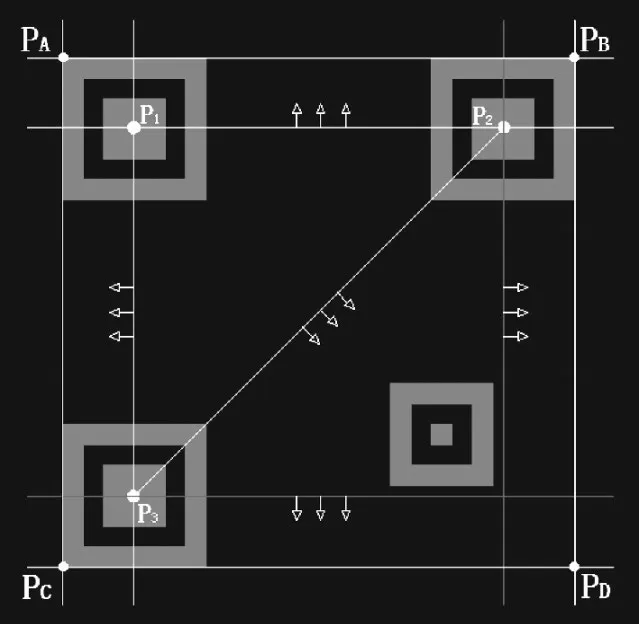
图4 直线最佳逼近法示意图

2 三维空间校正

利用辅助矩形进行平面矫正以及直线最佳逼近法提取出边界后，得到的图像仍为长方形(如图5 所示，其中AC ＞AB，由于主视图太长，这里简化)，需再次对图像进行三维空间的校正。校正的关键在于如何将长方形校正为正方形［9］。从图中可以得到公式(2)和公式(3):

联合式(2)、式(3)可得:sin(α)=n ×α/m，其中m和n 的值经过图像检测可以直接求得，α 的值一定在0至π/2 之间，并且是唯一的，可通过二分法求得α 的近似值。得到α 后，根据式(2)可求得R 的值为m/2α。

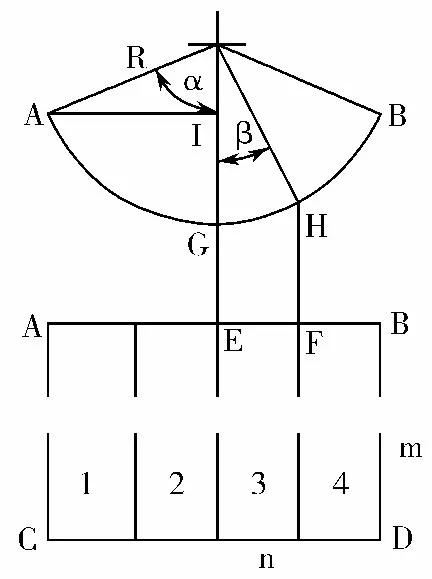
图5 区域还原算法示意图

由于QR 码的特征比较简单，当畸变不是很大时，没必要采取逐个像素映射还原的方法，采用区域分割还原法即可［10］。根据获取到的n/m 的比例，把提取出的QR 码图像以中线为基准分割成n 等分，分割结果如下:

图5 是将QR 图像分割成4 等分的示例，其余分割类似。采用区域还原就是将每一个区域进行不同程度的拉伸。这里以区域3 为例说明，如图有EF=n/4，sin(β)=EF/R，半径R 在之前已经求过了，所以可以很容易求出β，此时弧长GH=R×β。对于区域3，区域还原就是将EF 拉伸到弧长GH。对于其他3 个区域同样可以求得拉伸后的各自的长度。最后采用图像处理函数分别进行拉伸即可获得校正后的图像。

3 算法的实现

得到二维及三维校正后的图像后，还需要对图像进行二值化处理，其关键点是确定二值化的阈值，最大类间方差法在一般情况下能较好地解决该问题［11］。该方法将采集图像分为物体类和背景类，当2类间的灰度值方差取最大值时，对应的灰度值为二值化阈值。最后，使用文献［12］提出的一种基于图像熵的Otsu 改进算法，缩短计算时间，并使分割后的图像更加细腻，得到的标准QR 码图像如图6 所示。

图6 校正后的图像

最后使用Google 提供的ZXing 开源类库在Android 平台上实现了圆柱面QR 码识别软件［13］，使用安卓手机自带的摄像头完成拍摄及识别。流程图如图7 所示。

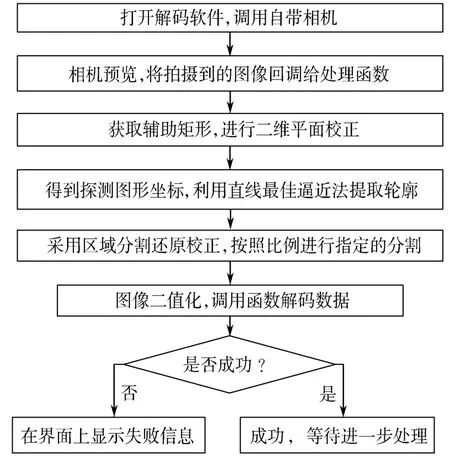
图7 柱面QR 码识别流程

4 结束语

本文通过几何学中添加辅助线的理念，站在平面几何的角度上提出了在QR 码外侧添加辅助矩形，利用它进行平面的校正，获取到正投影图像，对之后进行区域还原做好铺垫。当然本文所研究QR 码的场合是比较特殊的，即QR 码背景相对清晰，适宜添加辅助矩形而不影响其它内容。在三维校正时，又站在三维立体几何的角度上采用了效率相对较高的区域还原算法，而没有采用逐个像素重构，毕竟一个一个像素重新绘制是比较耗时的。最后在Android 平台上进行实现。

［1］Li Xiaochao，Shi Zhifeng，Guo Donghui.Reconstruct argorithm of 2D barcode for reading the QR code on cylindrical surface［C］// International Conference on Anti-Counterfeiting，Security and Identification(ASID 2013).2013:178-182.

［2］史志锋.基于三维透视变换的圆柱面QR 码识别方法［J］.现代电子技术，2014，37(8):16-18.

［3］GB/T18284，中华人民共和国国家标准—快速响应矩阵码(QR Code)［S］.

［4］张名，张建立.基于符号特征的QR 码识别算法［J］.计算机工程，2011，37(4):278-280.

［5］刘宏伟，严研.快速响应码的识别和解码［J］.计算机工程与设计，2006，26(6):1560-1562.

［6］冈萨雷斯.数字图像处理［M］.第2 版.北京:电子工业出版社，2007.

［7］谷口庆治.数字图像处理—应用篇［M］.北京:科学出版社，2002.

［8］杜秀伟，章兢，翟景瞳.基于轮廓特征的快速响应码定位与提取方法［J］.电子技术应用，2009，35(6):47-49.

［9］刘慧娟.一种快速响应码图形的分割和校正方法［J］.电子测量与仪器学报，2006(1):32-36.

［10］司国东，陈仲.柱面二维码识别算法的设计与实现［J］.现代计算机(中旬刊)，2013(8):25-27.

［11］Otsu N.Athreshold selection method from gray-level histograms［J］.IEEE Trans.on Systems Man and Cybernetics，1979，9(1):62-66.

［12］肖超云，朱伟兴.基于Otsu 准则及图像熵的阈值分割算法［J］.计算机工程，2007，33(14):188-189.

［13］陈二阳，雷霖.QR 条码图像识别及解码技术的实现［J］.电视技术，2013，37(7):16-19.