基于均衡更新蚁群算法的飞机排序调度

李媛祯，杨 群，段 汐

(南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

0 引言

随着航空运输业的飞速发展，空中交通日趋繁忙，空中交通管制(Air Traffic Control，ATC)的重要性愈加突出。飞机排序调度问题(Aircraft Arrival Sequencing and Scheduling，ASS)研究在空中交通繁忙的机场终端区，如何在保证飞机安全飞行间隔的前提下，有效地优化到港飞机着陆序和着陆时间，达到使飞机总延误最小、提高系统容量、增加飞行安全性等目标［1-2］。它是空中交通管制的一个关键问题。飞机排序调度中，到港飞机到达机场终端区以后，按照预定的进港路线飞行并着陆，n 架到港飞机的着陆次序可以有n!种排列，其组合优化是NP-难解问题。蚁群算法是一种能行之有效地解决组合优化问题的智能进化算法，本文拟采用一种基于均衡更新的蚁群算法处理飞机排序调度问题。

1 相关工作

随着我国经济迅速发展，航空运输量持续增加，合理有序地调度到港飞机的顺序是目前空中交通管制急需解决的问题。近年来，国内外学者已有许多相关研究，提出了许多解决飞机排序调度问题的方法［6-9］。传统飞机排序调度采用先到先服务(First Come First Service，FCFS)的调度算法［4］，这种方法基于航空管制员人工经验进行，在满足一定约束条件的前提下对飞机着陆序可以进行调整，保持大部分飞机之间的相对位置，最终确定着陆时间。虽然算法简单易行，但造成的飞机延误时间较大，不能很好地满足空中交通流量管制需求［16-17］。Hu 等［2-3，5］使用改进的遗传算法处理飞机排序调度问题，取得一定效果，但算法模型中未考虑实际旅客数量，没有区别对待不同载客量的飞机，忽略了不同载客量的飞机延误所带来的不同影响。Zhao［7］等将贪婪随机自适应搜索和蚁群算法相结合，处理非正常航班的再次调度问题，结合后算法能较好地发挥蚁群算法的正反馈特点，且具有较高鲁棒性，但该特殊情况并非当前空中交通管制的重要方面。Wang［14］采用Pareto 优化方法，构建一个数学模型，实现加权航班延误时间与延误时间数量之间的平衡，然后灵活地选择解决方案，从而达到优化飞机着陆序列的目的，然而未考虑到实际情况中搭载旅客数因素，这会造成旅客机场滞留的情况。

针对以上不足，本文提出一种信息素均衡更新的蚁群算法处理飞机排序调度问题:在安排飞机着陆序时，增加飞机实际载客量因素，对搭载旅客数量较多的飞机给予优先着陆概率，尽可能避免该到港飞机即将搭载的离港旅客滞留;同时，尽量保障飞机按照预期时间着陆，如已延误，则尽量缩短延误时间，减轻了管制员的负担，也提高飞行安全性。另一方面，对蚁群算法信息素局部堆积导致容易陷入局部最优解的缺陷，则改进信息素更新模式，使用均衡更新方法更新信息素，以求生成更优的到港飞机序列。

2 均衡更新蚁群算法

蚁群算法(Ant Colony Optimization，ACO)由意大利学者Marco Dorigo 于1992 年的博士论文中提出，最初应用于旅行商问题［11］。近年来，蚁群算法因其独特的正反馈机制和离散分布式特性，被众多学者应用于作业调度、车辆路径、网络路由、信息检索等方面［12］。飞机排序调度问题属于NP-难解问题，可以通过转化为作业调度问题或者旅行商问题来方便地求解［13］。

本文针对现有算法［1-10］的不足之处，提出一种均衡更新蚁群算法:

1)从旅客的实际利益出发，为提高航空运输服务质量，安排飞机着陆序时增加飞机实际载客量因素，使载客量大的飞机具有更早着陆的概率。

2)考虑到管制员负担较重会影响飞行安全性，尽可能减少飞机延误，减轻管制员的负担。

以上2 方面体现在均衡更新蚁群算法的转移概率和目标函数中，在转移概率中本文增加了相应的启发式信息，目标函数的计算考虑了旅客数和延误信息。

3)考虑到蚁群算法中信息素局部堆积，容易造成算法陷入局部最优解，改进蚁群算法的信息素更新过程，使用信息素均衡更新的方式，避免信息素局部堆积，使得算法能在解空间中更加充分地搜索，提高了算法的全局搜索能力，从而生成更优的解。

均衡更新蚁群算法流程如图1 所示。

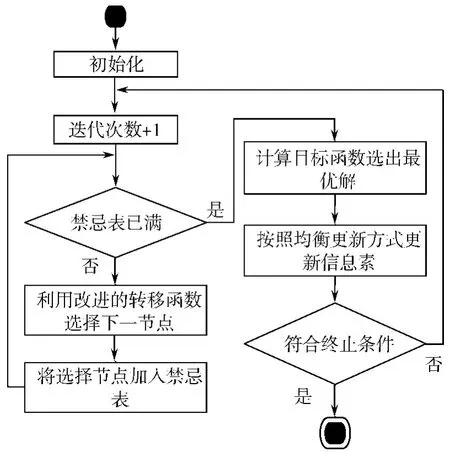
图1 均衡更新蚁群算法流程图

在均衡更新蚁群算法中，每只蚂蚁根据路径上的信息素和启发式信息计算转移概率，选择下一节点，即下一架到港飞机，并将此节点加入该蚂蚁所维护的禁忌表(禁忌表存放已遍历的节点)中，直到遍历完所有节点，此时可认为生成一个可行解。计算并比较本次迭代中所有蚂蚁生成的解对应的目标函数值，选择其中最优解作为当前迭代的最优解，并和迭代至今的全局最优解做比较，较优者为新的全局最优解。最后，每只蚂蚁根据全局最优解和自己构建的可行解之间的差异对信息素做均衡更新。

1.飞机排序调度模型。

在本文中，飞机排序调度模型如下，其目标是针对当T 时间内有n(n ＞0)架飞机待着陆时，在满足最小安全时间间隔限制基础上，安排合理的飞机着陆序列，使得含有飞机延误时间和延误旅客数参数的目标函数最小化。

定义1 G=(V，E)表示飞机排序调度模型，其中，V 表示待着陆飞机的节点集合，E 表示着陆飞机之间的先后关系的边集合。

其中，与模型有关的符号如下:

Sij:对于任意2 架连续到港飞机，较先着陆的飞机i 为前机，紧邻到港的飞机j 为后机，Sij表示前机i和后机j 之间的最小安全时间间隔。

Ai:飞机i 的实际着陆时间。

Ei:飞机i 的预期着陆时间。

Pi:飞机i 实际搭载的旅客数。

Iij:指示飞机i 和飞机j 之间的先后关系，i 为前机、j 为后机时为1，其余为0。

c:可容忍的飞机最大延误时间，为常量。

2.算法约束条件。

均衡更新蚁群算法求解时，模型和算法必须符合如下约束条件:

1)对于任意2 架到港飞机，或者i 为前机，或者j为前机，或者i 和j 之间不存在连续序列关系，即:

2)任意一架到港飞机i 实际延误时间不得超过可容忍的最大延误时间，即:

3)连续2 架飞机着陆时，若i 为前机，j 为后机，则需满足最小安全时间间隔:

4)任意2 架飞机i、j，到港过程中都必须满足最小安全时间间隔:

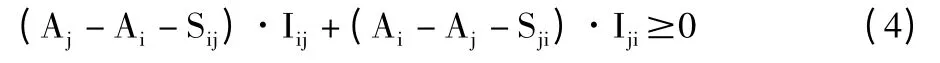
3.算法转移概率。

蚁群算法模拟自然界中蚂蚁种群行为，在算法中存在由一定个数的人工蚂蚁构成的搜索群体，每只蚂蚁逐步遍历节点直至生成单个解，蚂蚁每到达一个节点，都会计算转移到当前节点邻域中节点的概率，概率性地选择下一节点，并将选择后的节点加入该蚂蚁维护的禁忌表中。转移概率计算方式如下:

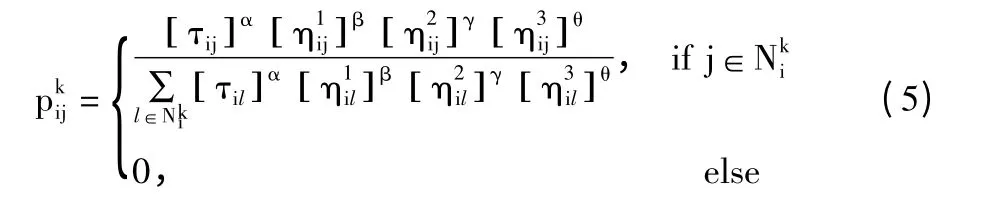
其中:

τij:代表节点i 到节点j 上的信息素;

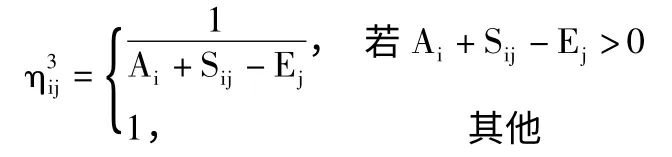
α:代表信息素的影响力因子;

β:代表安全时间间隔启发式信息的影响力因子;

γ:代表旅客数启发式信息的影响力因子;

θ:代表延误时间启发式信息的影响力因子;

本文中，蚂蚁选择下一架着陆飞机时，综合考虑了信息素、安全时间间隔、搭载旅客数以及飞机延误时间的影响，充分发挥了蚁群算法的正反馈特性，保证飞机降落的安全性，尽可能为绝大多数旅客提供高质量的航空运输服务，且减少飞机延误的可能也从一定程度减轻管制员的工作负荷。

4.算法目标函数。

根据上述描述，本文利用提出的算法，在给定时间T 内，利用蚁群算法中蚂蚁的遍历，安排飞机着陆序，使以下目标函数值最小:

该目标函数既考虑了飞机延误时间因素，也考虑了每架飞机实际载客量的因素，目的是得到使所有乘客延误总时间最小的飞机着陆序列，以便提供高质量的民航运输服务。

5.信息素均衡更新机制。

蚂蚁利用转移概率逐步构建出一个完整的可行解。首先，计算目标函数，即式(6)，并比较所有结果取其中最优者作为当前迭代最优解，也即局部最优解。然后，与迭代至今为止得到的最优解，即全局最优解做比较，其中较优者作为新的全局最优解。完成以上步骤后，用如下方法更新信息素:

1)根据全局最优解对应的目标函数值计算信息素增量，其中，fglobal_best是全局最优解对应的目标函数值，Q 是一个常量:

2)各个蚂蚁根据各自所构造的解和全局最优解之间的差异来均衡更新信息素，避免信息素局部堆积，增强算法全局搜索能力。更新规则如下:

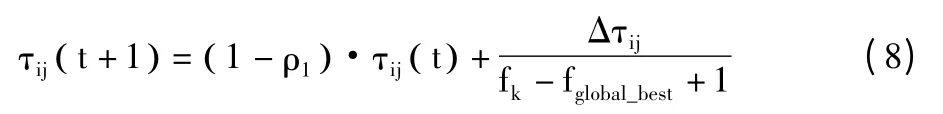
其中，ρ1是均衡更新信息素蒸发率，fk是蚂蚁k 所构造解对应的目标函数值。

3)采用得到最优解的蚂蚁，更新与之相关联的路径上的信息素，强化全局最优路径的影响。更新规则如下，其中，ρ2是全局更新信息素蒸发率:

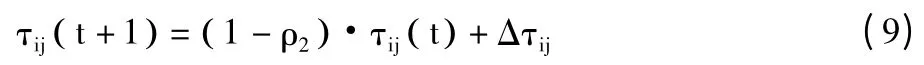
总之，上述方法从2 个方面提高算法的效率、优化算法得到的解。一是利用当前迭代的可行解和全局最优解之间的差异均衡地更新信息素，该方式既体现了蚁群算法利用已有搜索信息探索未知解空间的正反馈能力，又有效地避免了信息素局部堆积可能导致的陷入局部最优解问题。二是采用得到全局最优解的蚂蚁更新相关路径，进一步强化全局最优解的影响力，使得搜索朝着最优解存在的空间移动。

3 实验与结果

本文利用VC ++实现提出的算法，并与先到先服务(FCFS)算法以及文献［14］中侧重飞机延误时间和延误架次的蚁群算法求解的结果比较，评估均衡更新蚁群算法对飞机排序调度模型的求解结果，其中，文献［14］实验的目的主要是评价航空公司每天在飞机延误数量与平均时延，以验证其算法的有效性。限于篇幅，实验数据取国内某枢纽机场30 分钟内预期到港飞机信息，共计22 架飞机，实例具体数据见表1。

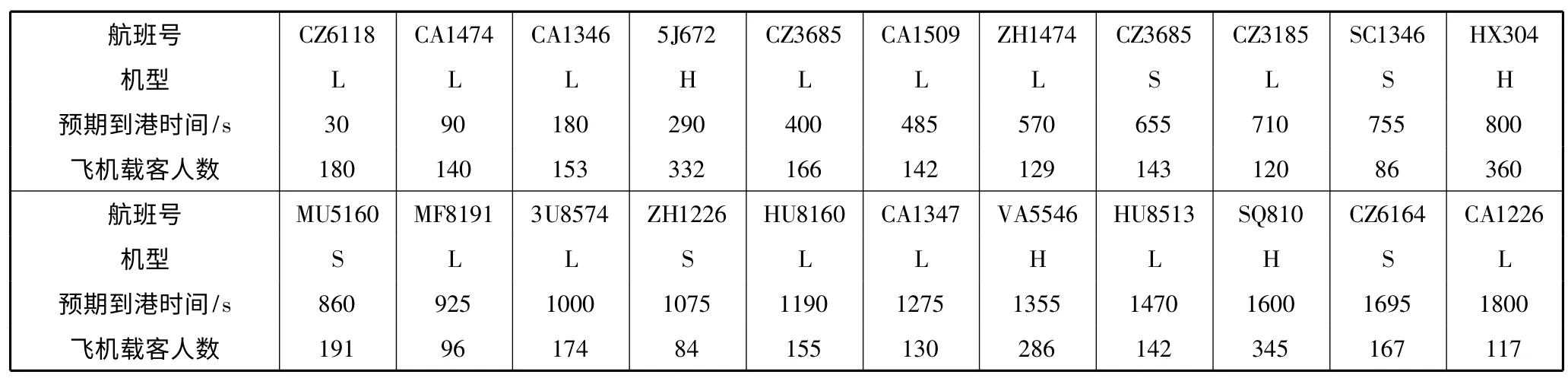
表1 预期到港飞机信息

利用表1 数据，分别取前5、10、16、22 架待着陆飞机数据进行对比实验(即n=5，10，16，22)，并取10次实验结果的平均值。本文算法参数设置为:迭代总次数NCMAX=100;蚂蚁总数M=20;信息素影响力因子α=1;安全时间间隔启发式信息影响力因子β=2;旅客数启发式信息影响力因子γ=2;延误时间启发式信息影响力因子θ=3;均衡更新信息素蒸发率ρ1=0.05;全局更新信息素蒸发率ρ2=0.1;常数Q=10n;a=70;b=0.2;c=1200。实验结果如表2，其中，列2～列4 分别为各算法求解n 架飞机排序后着陆的总用时，列5 表示本文算法运行耗时，列6、列7分别表示采用本文所提出的算法计算得到的n 架飞机排序后着陆总用时相对于FCFS、文献［14］所得的总用时降低的比率，其计算方法是:(被比较算法总用时-本文算法总用时)/被比较算法总用时。

由表2 可见，本文均衡更新蚁群算法求解飞机排序调度问题能取得优于先到先服务算法和文献［14］算法的解，优化后的飞机着陆序列完成时间比先到先服务算法最多可降低12.9%，比文献［14］降低4.7%。从上述实验数据还可以看出，本文算法计算得到的飞机着陆总用时与其他算法相比较，其降低的程度与待排序飞机数目没有直接关联，这是因为飞机之间的安全时间间隔占着陆总用时的绝大部分，而安全时间间隔由前后机机型决定，与飞机数量无关。另外，

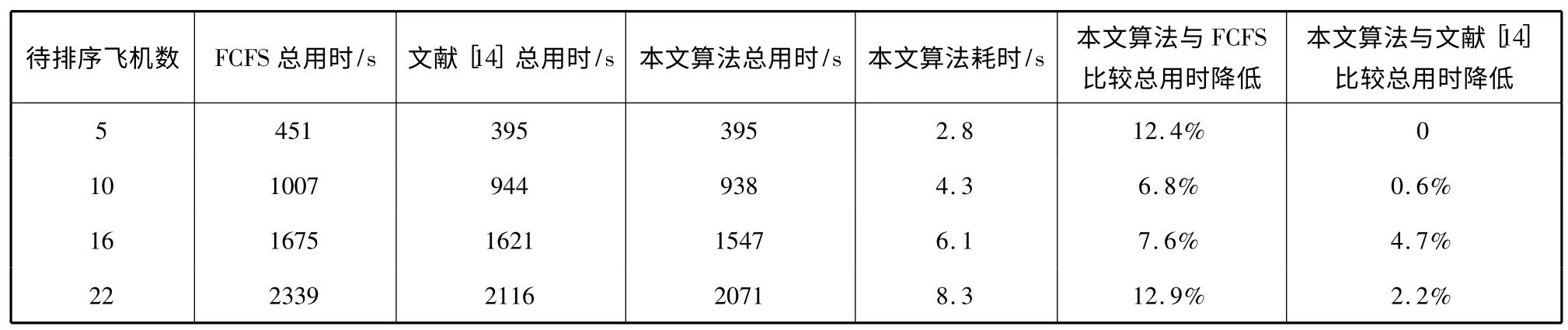
表2 不同算法实验结果

本文算法和文献［14］算法均考虑到延误时间对排序结果的影响，因此可以通过适当调整飞机顺序来减少延误发生，但本文算法还考虑到飞机实际搭载旅客数，优化时兼顾大部分旅客的航程正常进行，能从一定程度上避免到港飞机延误带来的离港旅客滞留，为来往旅客提供更好的服务;而文献［14］算法求解时倾向于减少飞机调换顺序的次数，优化过程不如本文算法灵活，效果也较本文算法差。本文算法还具有计算用时少的特点，因此可以为实时在线自动化空中交通管制提供支持。

总之，本文算法求解结果优于传统先到先服务算法和文献［14］算法，同时能加入飞机服务对象——旅客的切身利益因素，尽量保证为大部分旅客提供准点、高效的服务，较好地优化飞机着陆次序和时间，达到飞机延误时间最小化，有效提高系统容量。

4 结束语

中国民航运量位居世界第二［15］，如何在现有空域结构下优化飞机着陆顺序，提高运行效率，并且减少延误时间是一个重要的研究内容。飞机排序调度问题属于NP-难解问题，蚁群算法是一种能有效处理NP-难解问题的启发式算法。本文针对飞机排序调度问题，提出一种均衡更新蚁群算法，实现多约束优化。由于传统蚁群算法存在因信息素局部堆积导致易陷入局部最优解的不足，本文利用蚂蚁当前迭代计算所得可行解与全局最优解之间的差异，均衡地更新信息素，既保留计算所积累的经验，发挥蚁群算法的正反馈作用，又有利于探索更优解。实验结果表明，针对飞机排序调度问题，本文算法优于对比算法，优化后的排序可使飞机着陆序列完成时间减少12.9%，同时还兼顾了大部分旅客的时间，且计算用时较短，能为空中交通管制员实时在线协调管理提供支撑。

［1］Zhan Zhi-hui，Zhang Jun，Li Yun，et al.An efficient ant colony system based on receding horizon control for the aircraft arrival sequencing and scheduling problem［J］.IEEE Transactions on Intelligent Transportation Systems，2010，11(2):399-412.

［2］Hu Xiao-bing，Di Paolo E.Binary-representation-based genetic algorithm for aircraft arrival sequencing and scheduling［J］.IEEE Transactions on Intelligent Transportation Systems，2008，9(2):301-310.

［3］Hu Xiao-bing，Chen Wen-hua.Genetic algorithm based on receding horizon control for arrival sequencing and scheduling［J］.Engineering Applications of Artificial Intelligence，2005，18(5):633-642.

［4］Robinson J E，Davis T J，Isaacson D R.Fuzzy reasoningbased sequencing of arrival aircraft in the terminal area［C］// AIAA Guidance，Navigation and Control Conference.1997:1-11.

［5］Hu Xiao-bing，Di Paolo E A.A ripple-spreading genetic algorithm for the aircraft sequencing problem［J］.Evolutionary Computation，2011，19(1):77-106.

［6］Psaraftis H N.A dynamic programming approach for sequencing groups of identical jobs［J］.Operations Research，1980，28(6):1347-1359.

［7］Zhao Xiuli，Guo Yanchi.Study on GRAPS-ACO algorithm for irregular flight rescheduling［C］// IEEE 2012 International Conference on Computer Science ＆ Service System(CSSS).2012:266-269.

［8］刘洪，杨红雨，彭莉娟.基于分组的进近航班着陆调度算法研究［J］.电子科技大学学报，2013，42(4):615-620.

［9］赵嶷飞，朱潇，王红勇.终端区飞机排序的人工蜂群算法［J］.科学技术与工程，2013，13(31):9258-9262.

［10］冯兴杰，孟欣.基于免疫粒子群优化算法的航班着陆调度研究［J］.计算机工程，2012，38(13):273-279.

［11］Dorigo M.Optimization，Learning and Nature Algorithms［D］.Milan:Dipartmento di Elettronica，Politecnico di Milano，1992.

［12］Dorigo M，Birattari M，Stutzle T.Ant colony optimization［J］.Computational Intelligence Magazine，IEEE，2006，1(4):28-39.

［13］Bencheikh G，Boukachour J，Alaoui A E H.Improved ant colony algorithm to solve the aircraft landing problem［J］.International Journal of Computer Theory and Engineering，2011，3(2):224-233.

［14］Wang Shi-dong，Zhang Yue，Zhang Zhi-hai，et al.Multiobjectives optimization on flights landing sequence at busy airport［J］.Journal of Transportation Systems Engineering and Information Technology，2012，12(4):135-142.

［15］于剑，王文涛，李航.对中国航空公司中欧市场运量的影响分析［J］.中国民航大学学报，2011，29(1):42-45.

［16］Cao Song，Sun Fuchun，Hu Laihong，et al.Departure aircraft sequence optimization using EDA［J］.Journal of Tsinghua University Science and Technology，2012，52(1):66-71.

［17］许军海，何长青，王昭.机场终端区飞机排序的遗传算法［J］.信息系统工程，2013(10):132-134.