基于改进遗传算法的大规模TSP 问题求解方案

雷玉梅

(阜新高等专科学校，辽宁 阜新 123000)

0 引言

TSP(Traveling Salesman Problem)问题，也称旅行商问题或货郎担问题，是一个典型的NP(Non-deterministic Polynomial)完全问题。它不仅描述了商人从一个城市出发，经过其他多个城市，且只经过一次之后，又回到出发城市的问题，也是数学领域一个复杂的组合优化问题，更是诸多领域内许多复杂问题的概括的形式化描述。凡是可以抽象地表示为遍历且只遍历所有结点一次，最终回到初始结点，求代价最小的回路问题，都可以仿照求解TSP 问题的方法进行求解。因此，TSP 问题的解决方案在计算机理论和实际应用中得到广泛的关注。

目前解决TSP 问题的方法大致可以分为2 大类［1］，一类是拥有较好的数理逻辑和理论基础的精确的计算方法(Exact Algorithm)，能够找到问题的最优解，另一类是近似的计算方法(Approximation Algorithm)，没有严密的数理逻辑，但通常能够更为高效地求得可接受的问题的解，因此在实际中应用更为广泛，遗传算法就是一种典型的近似计算方法。

遗传算法是根据优胜劣汰的生物进化理论设计出来的一种优化的搜索算法，主要通过遗传染色体信息，选择对“环境”的“适应能力”高于父代的子代，直到适应能力满足一定的要求。高经纬等人在文献［2］中证明了使用遗传算法求解TSP 问题时具有结果准确、收敛速度快的特点。文献［3-9］从不同的方面对遗传算法进行改进，提升了其解决TSP 问题的能力。然而，对于大规模的TSP 问题，始终没有较好的解决办法，也吸引了越来越多的研究学者的关注。

本文结合启发式的思想和改进的遗传算法，提出了新的解决大规模TSP 问题的HG 方法，采用分而治之和启发式的初始化方法，利用改进的遗传算子，提高了遗传算法的性能，多个数据集上的实验结果证明了HG 算法的有效性。

1 相关概念

1.1 TSP 问题形式化描述

给定N 个城市的集合，城市用ci，i∈{0，1，...，N-1］表示，R=(c0，c1，...，cN-1)表示经过所有N个城市的一条路线，当路线R 满足公式(1)取得最小值时，R 即为TSP 问题的最优解:

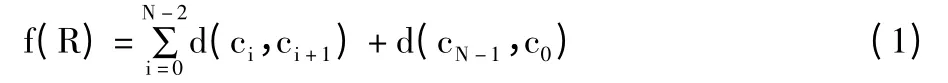
其中，d(ci，ci+1)表示城市ci与城市ci+1之间的距离，f(R)表示路线R 的距离。

解决TSP 问题的目标就是找到一条路线R*，使得f(R*)取得最小值。对于N 个城市的TSP 问题，采用全局搜索的方式，可行的组合有(N-1)!种，当N 变得很大时，全局搜索的方法已经不可能解决TSP 问题。

1.2 遗传算法

遗传算法首先对问题中的参数集进行编码，形成初始种群，计算适应度，然后通过染色体信息的代代相传(利用选择、交叉和变异算子不停地进行算法迭代)搜索具有最高适应度的个体，算法流程可用图1 表示。

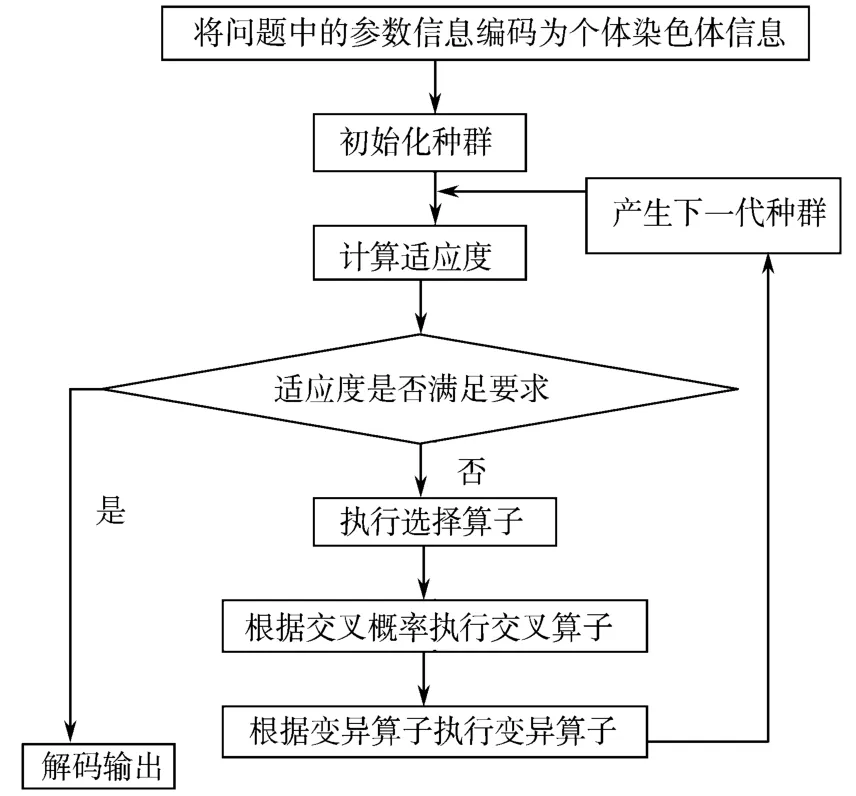
图1 遗传算法流程图

2 HG 算法

2.1 聚类

本文沿用分而治之的思想解决大规模的TSP 问题，根据坐标位置进行聚类操作，把相对位置较近的城市划分到一个类簇(聚类的结果)中。城市之间的“相似性”采用欧式距离描述，如公式(2)所示:

其中，p 表示结点的属性的数量，这里是2(城市的经度和纬度)，wij表示结点ci与cj的相似性。在TSP问题中，结点之间的欧式距离表示城市之间的位置距离，因此聚类操作会把距离较近的城市划分到同一个类簇，符合进行聚类操作的初衷。

经过聚类操作，把一个大规模的TSP 问题，划分为多个类簇中的子TSP 问题，然后采用本文改进的遗传算法求解各个子TSP 问题。

2.2 编码与初始化

本文采用序号编码的方式，把每个类簇中的城市编号为1，2，3，…，ni，ni表示第i 个类簇的城市数量。一条路径编码为一条染色体，用1～ni的任一排列组合表示。

初始化过程用来构造初始的种群(染色体的集合)，初始化结果的好坏，一定程度上决定了遗传算法收敛所用的时间。传统的遗传算法中，一般采用随机的方式产生初始化种群，但是这种方法的不稳定性极高，遗传算法的收敛可能需要很长时间。Osaba 等人在文献［9］中指出，使用启发式的初始化函数能够有效地提升遗传算法的性能。本文就采用了NN［10］的启发式初始化函数，具体地，在类簇i 中随机选择一个起始城市c0∈{1，2，...，ni}，然后根据公式(3)依次选择剩下的ni-1 个城市，组成初始路线:

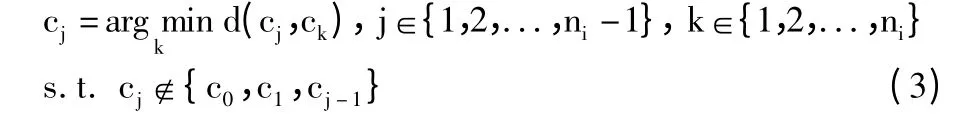
HG 的初始化方法，使最初的路线拥有较高的适应度，有利于从根本上提升算法的收敛速度以及优化收敛结果。

2.3 适应度函数

适应度是用来评价个体对“环境”的适应能力，适应度越高，说明适应能力越强。在TSP 问题中，适应度可以用路线的距离来表示，路线的距离越短，说明路线越优。为方便后续的遗传算子的操作，HG 方法采用公式(4)所示的适应度函数:

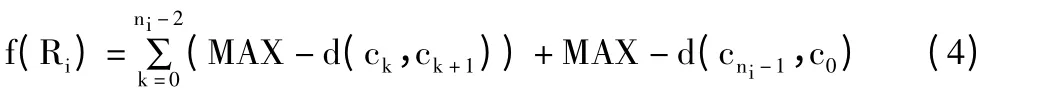
其中，MAX 表示无穷大，f(Ri)表示种群中个体i 的适应度，其值越大，表示个体的适应能力越强。

2.4 交叉算子

交叉是指父代2 个个体的部分染色体信息进行互换，重组为新的个体的操作，在生物进化的过程中发挥着核心作用。遗传算法中的交叉算子同样发挥着重要作用，但不是任意2 个父代的个体都会进行交叉操作，交叉行为的发生有一定的概率，发生交叉行为的个体占种群个体总数的比例称为交叉率。由于HG 方法采用的是序号编码，因此采用单亲遗传的方法，在单条染色体内进行单点交叉操作。对满足交叉率的染色体，利用公式(5)选择交叉点:

其中，tik表示染色体i 的第k 个交叉点，S 表示交叉点的总数。由公式(4)可知，根据路线Ri中连续2 个城市之间的距离最远的S 个位置，依次选择S 个交叉点，把染色体i 切成S +1 个片段，然后将这S +1 个片段重新组合成完整的一条染色体。

HG 的交叉算子消除了个体中对适应度影响最大的染色体信息(切断路线中距离最远的连续的2 个城市)，有利于促进算法的收敛进程，同时能够增加种群的多样性，有利于避免过早收敛的现象。

2.5 变异算子

变异算子是指对染色体上某位置的信息进行变动，比如，交换路线上任意2 个不同城市的位置。跟交叉操作一样，变异操作同样有变异率的约束，是指发生变异的个体占种群中个体总数的比例。传统的遗传算法通常为变异率选择固定的数值，而HG 算法利用公式(6)定义动态的变异率:

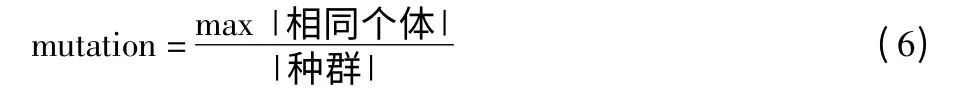
其中，mutation 表示变异率，分子表示种群中染色体信息相同的个体数目的最大值，分母表示种群的数量。比如，随着算法的迭代，在某一世代的种群中染色体A 出现了2 次，染色体B 出现了3 次，且A≠B，且没有其他染色体对应多个个体，则公式(6)的分子值为3。

在满足变异率的前提下，随机交换染色体2 个位置的信息，而且在算法迭代初期，只针对染色体的前段信息进行变异操作，以扩大解空间的搜索范围，到算法迭代后期，则只变异染色体的后段信息，否则可能会影响算法的收敛。

HG 算法的动态变异算子，保证了种群的多样性，有利于避免过早收敛的问题，同时还保证了较大的解空间的搜索范围和较好的收敛结果。

2.6 选择算子

选择算子用来把种群中的优良个体直接选入下一代。轮盘赌方法是一种简单又常用的选择方法，每个个体对应一个选择概率，适应能力强的个体，选择概率大，适应能力低的，选择概率小，选择概率通过公式(7)计算:

其中pik表示种群i 中个体k 的选择概率。

由公式(7)可知，种群中所有个体的选择概率之和为1，因此可以通过累加的方式为每个个体确定一个概率区间。比如个体1 的选择概率为0.1，个体2的选择概率为0.2，则个体1 的概率区间为0～0.1，而个体2 为0.1～0.3。然后根据0～1 区间内的一个随机数，确定被选中的个体。

2.7 全局TSP 问题的解

在求得各子TSP 问题的解之后，需要将它们集成为全局的TSP 问题的解，即把各个类簇连接起来。HG 方法仿照单链接的聚类方法，在2 个待连接的类簇之间应用2 次单链接方法，把2 个类簇连接起来，但要求2 次单链接方法选中的4 个点必须是2 对点，即同一个类簇中的2 个点是直接相连的。单链接聚类是指根据2 个类簇对象之间的最短距离连接类簇的方法，具体可由图2 表示。

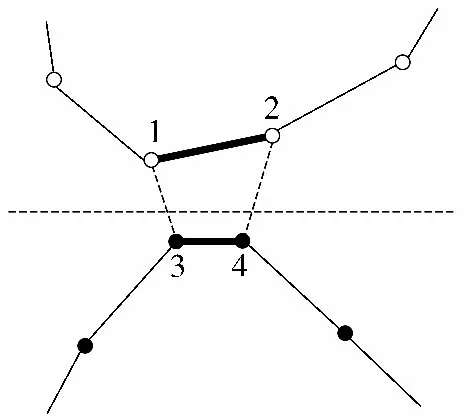
图2 聚类连接

图2 中，中间的虚线分割的上下2 个类簇就是待连接的类簇。2 次单链接方法，分别可以找到结点1和3 之间的虚线，以及结点2 和4 之间的虚线，然后把结点1 和2 之间以及结点3 和4 之间的黑色加粗连线剪断，把结点1 和3 以及结点2 和4 连接起来，就成功地把2 个类簇连在了一起。实际操作过程中，是先找到2 个类簇距离最近的4 个点，如图2 中的1，2，3，4，然后比较1-3，2-4 的距离之和与1-4，2-3 的距离之和，选择较短的一组进行连接。这样就把2 个类簇连接成了一次类簇，再继续与其他的类簇连接，就可以得到全局的TSP 问题的解。

2.8 HG 算法流程

根据前文的阐述，可用表1 描述HG 算法的流程。

表1 HG 算法流程

3 实 验

为了验证HG 算法解决大规模的TSP 问题的性能，本节选用标准问题库 TSPLIB 的 A280 和NRW1379 两个数据集进行实验，采用标准的遗传算法(SGA)以及Le 等人［10］和金聪［11］提到的利用启发式思想改进的遗传算法作为对比算法。文献［10］主要将NN 的启发式思想用于初始路径的选取(HNN)，而文献［11］则选用梯度寻优技术对变异算子进行了改进(H-GO)。

实验中选用k-means 的聚类方法［12］，A280 数据集聚成10 个类簇，NRW1379 数据集聚成25 个类簇。实验均在Intel i5 处理器、2G 的PC 机上运行。

方便自学：教师应根据学员的现有水平从互联网上筛选适宜的视频资料帮助学员课后复习消化，如“交流接触器工作原理及内部结构”视频资料。

图3 和图4 分别展示了HG 和H-NN 算法在2 个数据集上随着迭代次数的增加，所计算出来的全局联通路径的长度的变化，而图5 和图6 则是与SGA 算法以及H-GO 算法的对比结果。

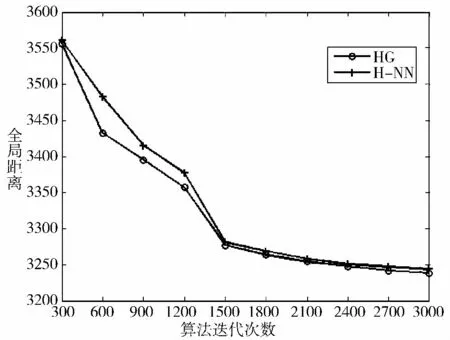
图3 路径长度随迭代次数的变化(A280)

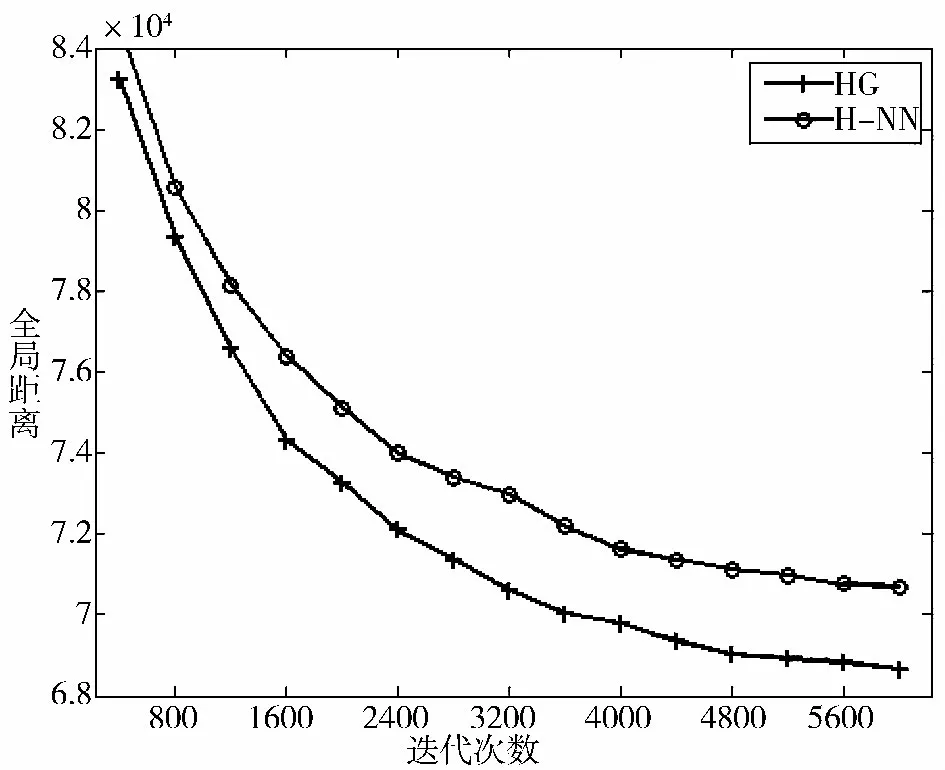
图4 路径长度随迭代次数的变化(NRW1379)

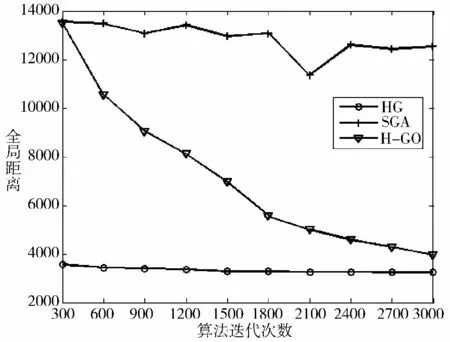
图5 HG VS(SGA ＆＆ H-GO)(A280)

图6 HG VS (SGA ＆＆ H-GO)(NRW1379)

从图3～图6 可以看出，随着迭代次数的增多，HG 算法计算得到的路径长度逐渐减小。在A280 数据集上，HG 算法经过3 000 次迭代之后，路径长度已减小到3 200 左右，而SGA 算法仍徘徊在13 000 附近，大概是HG 计算结果的4 倍。H-NN 与HG 算法的效果比较接近，但H-GO 算法由于采用了梯度优化的方法，在算法迭代后期，收敛速度较慢。在NRW1379 数据集上，HG 算法经过5 000 次迭代，路径长度已减小到68 000 左右，而SGA 算法的计算结果却仍相当于HG 的7 倍之多。H-NN 算法由于并没有考虑样本的多样性，出现了过早收敛的趋势，而HGO 算法同样存在后期收敛速度减缓的问题。此外，SGA 算法在A280 数据集上表现出了不稳定，距离长度曲线有回升的情况，这是由于算法运行一段时间后，路径的前段序列已接近最优，而在变异算子随机交换了2 个结点之间的顺序之后，使得原本较优的路径变差所导致的，采用动态变异算子的HG 算法就没有出现这种情况。

迭代次数的增加，必然伴随着运行时间的增加，图7和图8 展示了算法计算结果随着运行时间的变化。

图7 路径长度随运行时间的变化(A280)

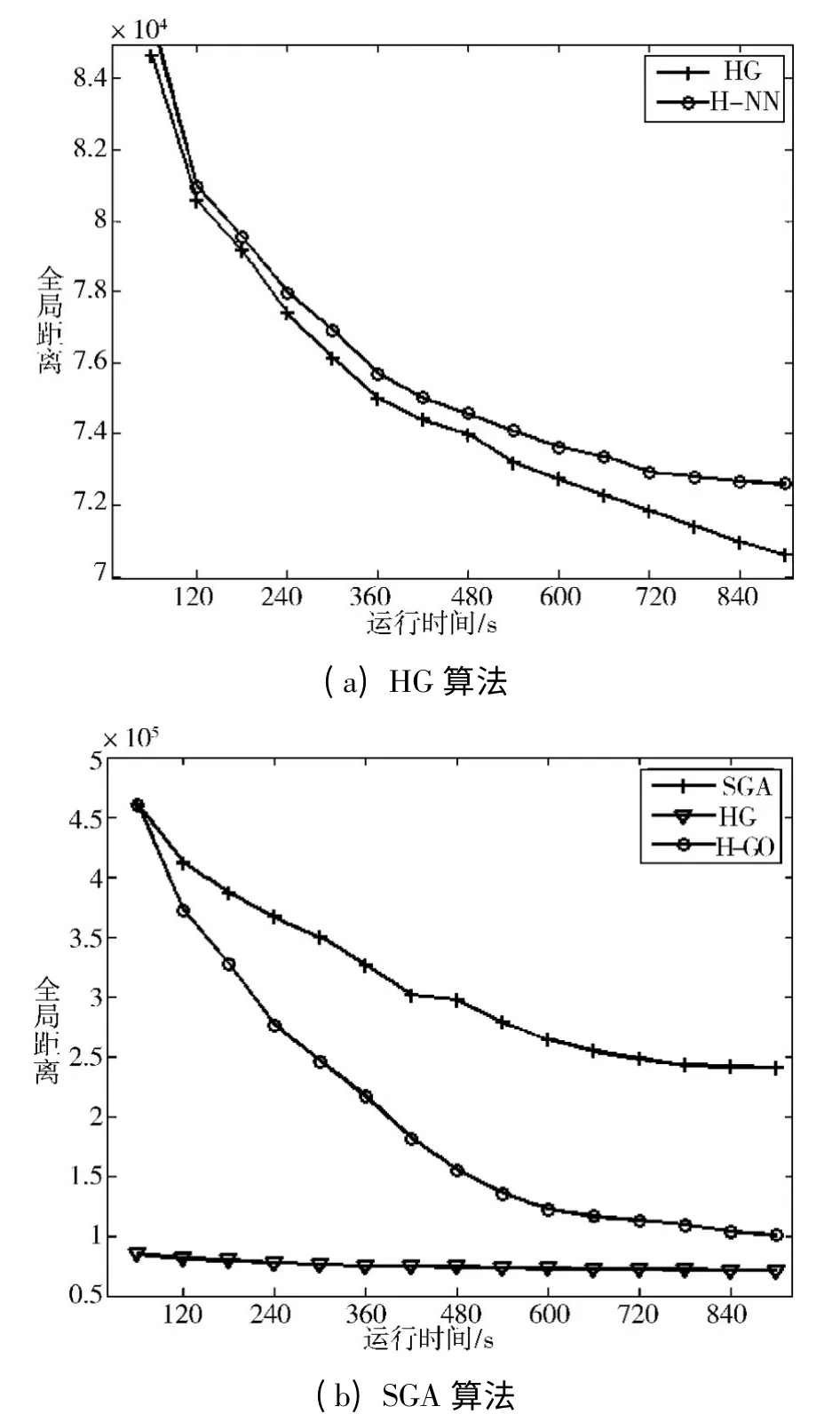
图8 路径长度随运行时间的变化(NRW1379)

从图7 和图8 中可以看出，随着运行时间的增加，HG 算法和SGA 算法计算的路径长度大体都呈下降趋势，但两者之间仍存在很大差距。例如在NRW1379 数据集上，当HG 算法的计算结果达到70 000 左右时，SGA 的计算结果还停留在250 000 附近，并且有出现过早收敛的迹象，而HG 算法则始终呈现较好的下降趋势。在图7 和图8 中，H-NN 算法过早收敛的问题和H-GO 后期收敛速度缓慢的问题表现的更加明显。

此外，为了直观、明显地观察HG 算法分而治之的思想，以及各个类簇连接的效果，图9 展示了NRW1379 数据集上HG 算法在迭代5 000 次之后的路径(并没有把各个聚类连接)，而图10 则展示了A280 数据集上类簇连接前后的路径结果图，同样证明了HG 算法的有效性。

图9 NRW1379 数据集路径

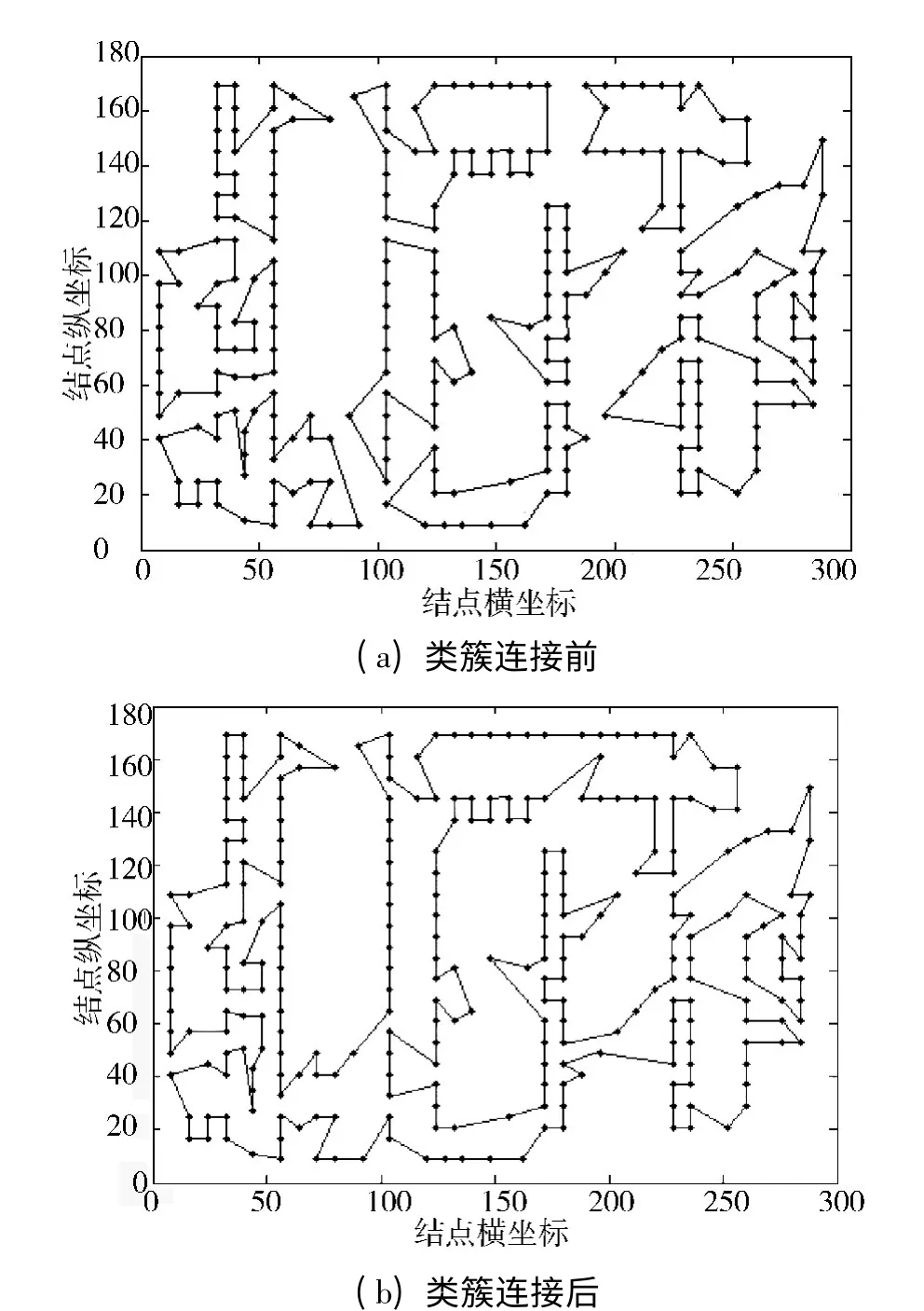
图10 A280 数据集路径

从图9 和图10 中可以分析出，最终算法的计算结果，受聚类结果的影响很大。表2 给出了2 个数据集上进行20 次实验所统计的HG 方法计算的全局路径长度的均值和均方差。

表2 HG 全局路径长度均值与均方差

其中，MSE 表示均方差，AVG 表示均值，N 表示进行实验的次数，此处取20。

实验过程中可能出现多次实验的聚类结果不尽相同的情况。因此，如何选择聚类算法，聚类的数量如何确定，以及是否存在最适合TSP 问题的聚类方法，这些都将成为笔者后续研究的课题。

4 结束语

大规模的TSP 问题不仅描述了旅行商人的路径选择问题，同时也是计算机、物流等诸多领域的复杂非线性问题的抽象模型。本文提出的HG 算法，化繁为简，把大规模的TSP 问题分割成多个子TSP 问题，并利用改进的遗传算法对各子问题求解，高效地解决了大规模的TSP 问题，同时有效地解决了过早收敛的问题。在标准问题库TSPLIB 的多个数据集上的实验结果，验证了HG 算法的有效性。

［1］Li Ying，Ma Kai，Zhang J iong.An efficient multicore based parallel computing approach for TSP problems［C］// 2013 the Ninth International Conference on Semantics，Knowledge and Grids (SKG).2013:98-104.

［2］高经纬，张煦，李峰，等.求解TSP 问题的遗传算法实现［J］.计算机时代，2004(2):19-21.

［3］张煜东，吴乐南，韦耿.智能算法求解TSP 问题的比较［J］.计算机工程与应用，2009，45(11):11-15.

［4］Yu Yingying，Chen Yan，Li Taoying.A new design of genetic algorithm for solving TSP［C］// Proceedings of the Fourth International Joint Conference on Computational Sciences and Optimization.2011:309-313.

［5］王斌，李元香，王治.一种求解TSP 问题的单亲遗传算法［J］.计算机科学，2003，30(5):73-75.

［6］李茂军，朱陶业，童调生.单亲遗传算法与传统遗传算法的比较研究［J］.系统工程，2001，19(1):61-65.

［7］Chen Junhong，Hu Junxiang，Zhen Xunyan.Application of improved partheno-genetic algorithm in distribution network switch optimal planning［C］// 2010 International Conference on Electrical and Control Engineering(ICECE).2010:467-470.

［8］Yang Jinqiu，Yang Jiangang，Chen Genlang.Solving largescale TSP using adaptive clustering method［C］// The Second International Symposium on Computional Intelligence and Design.2009:49-51.

［9］Osaba E，Carballedo R，Diaz F，et al.On the influence of using initialization functions on genetic algorithms solving combinatorial optimization problems:A first study on the TSP［C］// 2014 IEEE Conference on Evolving and Adaptive Intelligent Systems (EAIS).2014:1-6.

［10］Le Ny J，Feron E，Frazzoli E.On the Dubins traveling salesman problem［J］.IEEE Transactions on Automatic Control，2012，57(1):265-270.

［11］金聪.启发式遗传算法及其应用［J］.数值计算与计算机应用，2003，24(1):30-35.

［12］戴文华，焦翠珍，何婷婷.基于并行遗传算法的K-means聚类研究［J］.计算机科学，2008，36(6):171-174.

［13］戚玉涛，刘芳，焦李成.求解大规模TSP 问题的自适应规约免疫算法［J］.软件学报，2008，19(6):1265-1273.

［14］赵连朋，金喜子，王娜，等.求解超大规模旅行商问题的纵深遗传算法［J］.计算机工程与应用，2009，45(4):56-58.

［15］左国才，杨金民.K-means 算法在电信CRM 客户分类中的应用［J］.计算机系统应用，2010，19(2):155-159.

［16］温光辉，王明旭，郭嗣琮.一种求解TSP 问题的新型遗传编码方案［J］.科学技术与工程，2006，6(2):206-208

［17］滕奇志，唐棠，何小海，等.基于交换-单亲遗传算法的砂岩三位显微图像重建［J］.数据采集与处理，2010，25(3):364-368.