基于空域NSS 的无参考图像质量评价
夏裕建,孙 涵
(南京航空航天大学计算机科学与技术学院,江苏 南京 210016)
0 引言
自然图像指的是通过设备获取的客观世界的图形化描述,是对客观世界的真实描述,例如风景人物照、卫星遥感图等。与计算机生成的人工图像在统计上毫无规律的情况不同,自然图像被发现存在着内在的统计规律,已知的自然图像特性有以下几点:自相似性、尺度不变性、非高斯性和边缘主导特性、高维奇异性[1]。
自相似性是指自然图像的局部和全局较为相似,尺度不变性指的是自然图像的统计规律并不随图像尺寸的变化而变化,边缘主导性指的是Ann B.Lee和David Mumford[2]发现的边缘占据自然图像中的主导部分的特性,高维奇异性指的就是图像的边缘实际上是非连续点连接而成的曲线而不是孤立的非连续点。
近几年来,研究人员也建立了不少统计模型来描述自然图像的统计特性,并对无参考图像质量评价进行了深入的研究,提出了一些有效的无参考的图像质量评价方法。无参考图像质量评价方法主要可以分为针对特定失真类型的无参考图像质量评价算法和通用的无参考图像质量评价算法2 种。其中,自然场景统计(NSS)模型在无参考图像质量评价算法中得到成功的应用,使得NSS 模型受到越来越多的关注。
针对特定失真类型的无参考图像质量评价需要已知图像失真类型来对图像质量进行评价。Wang 等人针对JPEG 压缩图像,计算平均块边界的差异、块内活动以及零交叉密度,通过函数拟合方法来计算图像质量[3]。Narvekar 等人提出JNB(Just Noticeable Blur)模型得到模糊图像的质量评价方法[4]。Z.M.P.Sazzad 等人提出了针对JPEG 2000 失真图像的质量评价模型[5]。X.Zhu 等人基于局部梯度信息建立模型,提出了针对图像模糊和噪声的评价方法[6]。H.R.Sheikh 与A.C.Bovik 等人利用NSS 模型来预测JPEG2000 压缩过的图像的质量[7]。
而通用型无参考图像质量评价不需要已知图像失真类型,具有更广泛的应用价值。Moorthy 和Bovik提出了一个基于两步模型的NR-IQA 算法BIQI[8],包括失真类型分类以及针对特定失真类型的质量评价步骤,其中也使用了NSS 特征。后来,Moorthy 和Bovik 又利用该模型在小波域提取出相关NSS 特征来对图像质量进行预测,提出DIIVINE[9]算法。Saad 等人提出了BLIINDS-II[10]算法,该算法在离散余弦变换域提取NSS 特征来对图像质量进行评价。Mittal等人提出BRISQUE[11]算法,该算法利用局部归一化亮度因子的NSS 特征来量化图像中的失真,提取特征之后利用SVM 和SVR 来评价图像质量。Bovik 等人提出NIQE[12]算法,该算法利用BRISQUE 算法中提取出来的特征,利用多元高斯模型来建立模型拟合提取出的特征,最后计算从失真图像块中提取的拟合MVG 模型特征与从自然图像集中提取的特征间的距离作为图像质量的评价。NIQE 算法不需要对失真类型做出判断,也无需对主观分值进行训练,实现了盲评价。
以上算法中,基于特定失真类型的无参考图像质量诊断算法需要事先知道图像的失真类型,这在实际应用中是比较困难的。而通用型算法则大多需要利用已知主观评分的图像,采用机器学习的方法训练数据得到模型。NIQE 算法无需这些过程,但是其评价性能一般,且耗时也较长。本文认真研究了以上算法,在NIQE 算法的基础上进行改进,利用梯度强度代替NIQE 算法中的方差来选取自然图像的兴趣区域,然后提取NSS 特征进行建模。实验证明,本文的算法与NIQE 相比,Pearson 相关系数和Spearman 相关系数有所提高,与主观评价结果更为一致。
1 基于兴趣区域提取的无参考图像质量评价方法
改进的算法描述如下,首先利用人工选取的自然图像来建立自然图像的多元高斯分布(Multivariate Gaussian,MVG)模型。具体建模步骤如下:
1)对自然图像进行预处理,灰度化之后计算图像的归一化亮度系数;
2)对预处理后的图像进行分块处理,同时计算图像的梯度信息;
3)根据梯度强度进行兴趣区域的选取;
4)再在选取的图像块中提取出建立模型所需要的空域NSS 特征;
5)根据提出来的空域特征建立自然图像的MVG模型。
然后根据同样的步骤提取测试图像的空域NSS 特征,建立测试图像的MVG 模型,对于测试图像不需要选取兴趣区域的步骤,具体原因见1.4 节相关说明。
最终根据建立的自然图像和测试图像的MVG 模型,计算模型之间的距离,即测试图像与自然图像在NSS 规律上的偏离程度,并用此偏离程度来度量测试图像的质量。
下文将对建立MVG 模型的各个步骤逐一进行详细的说明。
1.1 预处理阶段
对图像进行预处理主要是为了计算出图像的归一化亮度系数。预处理首先将彩色图像转为灰度图像,然后根据图像分块大小进行裁剪图像边界的处理,保证分块阶段顺利进行并减少计算量,然后对图像的每一个像素通过以下公式来计算图像归一化亮度系数(i,j)。
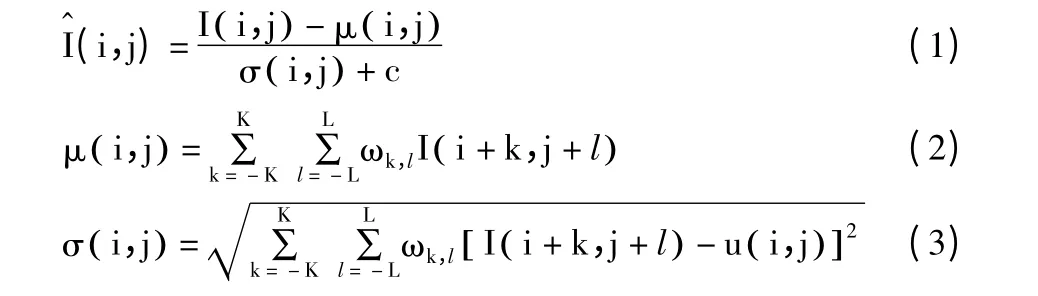
在式(1)~式(3)中,I (i,j)为对应的原始图像的灰度值,i∈{1,2,…,M},j∈{1,2,…,N},M 和N 分别为图像的高度和宽度,c 为一个较小的常量,是为了防止分母接近于0 的时候造成的计算结果不稳定的情况。μ (i,j)和σ (i,j)分别为加权的均值和方差,维圆对称高斯加权函数。求得的归一化系数被称之是一个二为归一化亮度(MSCN)系数。
Ruderman[13]认为自然图像的归一化亮度系数的统计特征趋向于服从广义高斯密度分布,而对于引入失真的图像,该归一化亮度系数的统计分布就会偏离高斯分布,所以这种偏离的程度就可以用来度量图像的失真程度。本算法思想就是通过比较测试图像和自然图像的归一化亮度系数的不同,计算测试图像和自然图像的归一化亮度系数的距离来评价图像质量。
原始图像及预处理过后的灰度图像如图1 所示,对照原图中添加的线条可以看出,灰度图像较原图右侧和下侧都有被裁剪的部分。

图1 原始图像与预处理后的灰度图像对比
1.2 兴趣区域提取
由1.1 节计算出图像的归一化亮度系数之后,对自然图像进行分块,分块大小为P ×P。后续提取图像的空域NSS 特征就是从各个分块图像中分别提取的,由于人眼更倾向于从图像中更清晰的部分来判断图像质量高低,所以本文对分块后的图像提取兴趣区域,选择相对更清晰的图像分块来进行后续的空域NSS 特征提取。进行兴趣区域提取之后,由于只需要对图像兴趣区域中的图像块进行特征提取,能提高算法性能。
本算法中提取图像兴趣区域是提取出图像中的高频部分以选取图像中的清晰区域,图像的清晰度可以看作图像细节的保真程度,边缘细节部分保留的越多,图像越清晰。目前清晰度评价方法主要有基于空域的梯度函数算法、基于频域的频域变换算法以及基于图像信息的熵函数评价算法。本算法是基于提取空域的NSS 特征,采用了基于空域的梯度函数的算法来进行图像清晰度评价准则最终用来进行兴趣区域的选取。
本文采用的提取兴趣区域的算法首先利用差分代替求导计算图像的水平、垂直方向的梯度值,具体计算公式如式(4)、式(5)所示:

式(4)、式(5)中,输入图像为经过上文预处理步骤后的处理过边界的灰度图像,I(x,y)为该灰度图像的亮度值。ΔxI(x,y)与ΔyI(x,y)分别为图像点的水平和垂直方向的梯度值。
然后利用上面计算得到的水平和垂直梯度值计算得到图像的梯度算子,具体计算公式如式(6):

式(6)中G(x,y)代表图像的梯度算子即本文使用的清晰度评价值,式中min 函数是进行越界处理的步骤,即将计算得到梯度大于255 的像素点赋值为255。然后对上文计算得到的梯度图像进行二值化,最终得到二值化后的图像。最终求得的梯度图像及二值化图像如图2 所示。

图2 梯度图像及二值化图像示意图
本文把通过上述步骤得到的二值化图像作为最终提取兴趣区域的基础,通过确定图像块是否位于二值化图像的兴趣目标内来选取兴趣区域。对于图像块的选取,采用的原则是只要图像块中有超过一定比例的像素点在兴趣目标内,则认为该图像块对于质量评价是有效的,选定该图像块作为后续特征提取的输入。具体公式如式(7)所示:

式(7)中G(i,j)为二值化图像的像素值,取值为1 或者0;row 和col 分别为预处理步骤中对图像进行分块得到的图像块的行和列的宽度;m 和n 分别为进行预处理之后的图像的长和宽;γ 为本文求得的图像块兴趣相关度的评价值。对于一个图像块,使用取舍原则取其中γ 值大于一定值的图像块作为兴趣图像块。
最终原图及提取的兴趣区域示意如图3 所示,本文选取了NIQE 中选取自然图像清晰区块的算法效果图进行对比,可以看到本算法基本可以选取到图像中的兴趣目标,对于目标兴趣区块来说比NIQE 算法选取的目标兴趣区块更为完整、合理。

图3 本文算法与NIQE 算法求得的兴趣图像块对比
1.3 空域特征提取
经过以上步骤的处理,得到兴趣区域内的图像分块,用于建立MVG 模型的空域NSS 特征就是从这些图像块中提出来的。研究发现,广义高斯密度函数(Generalized Gaussian Distribution,GGD)能够有效地捕获自然图像和失真图像的MSCN 系数的统计规律[14]。广义高斯密度函数如式(8)所示:
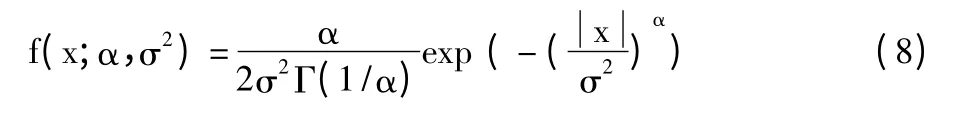
式(8)中,Γ(·)是gamma 函数。
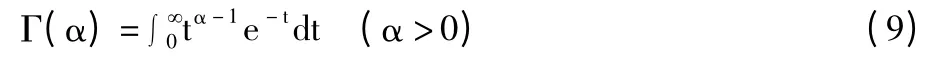
式(9)中参数α 决定了高斯分布的形状,σ2决定了高斯分布的方差,当α 为1 时,该分布就退化为拉普拉斯分布。
因此,对于一幅图像,GGD 模型提取了2 个参数(α,σ2)来评价图像质量,这2 个参数可以使用文献[15]中提到的基于时刻匹配的方法进行估算。
观察发现,自然图像相邻像素归一化亮度系数的乘积也符合一定的统计规律,可以表示图像的结构信息,而失真的引入会减弱这种结构性,因此,相邻像素的归一化亮度系数乘积也可以用来评价图像的质量。
本文对自然图像,在水平、垂直、主对角线、副对角线4 个方向提取结构信息,具体如下:
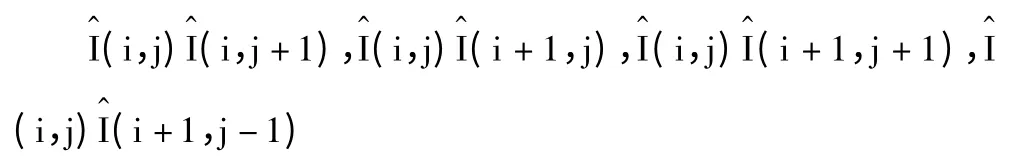
其中i∈{0,1,…,M-2},j∈{1,2,…,N-2},M 和N分别为图像的高度和宽度。
图像中相邻像素的归一化亮度系数乘积可以用非对称的广义高斯模型(Asymmetric Generalized Gaussian Distribution,AGGD)来近似模拟[16]。零均值的非对称广义高斯分布的表达式如式(10)所示:

AGGD 参数可以使用文献[16]中提到的基于时刻匹配的算法进行估算。AGGD 的平均值η 也提取出来作为特征:

这样,对于每一幅图像,在灰度空间对MSCN 系数建立GGD 模型提取2 个特征(α,σ2),并在水平、垂直、主对角线、副对角线4 个方向计算对相邻像素的MSCN 系数乘积建模,在每个方向上提取(η,v,)四个特征,共有18个特征用于评价图像的质量。为了更好地捕获结构信息,该方法又对图像进行2 倍下采样,使用同样的方法再提取出18 个特征,最终得到36 维的特征向量用于最终的质量评价,提取出的特征如表1 所示。
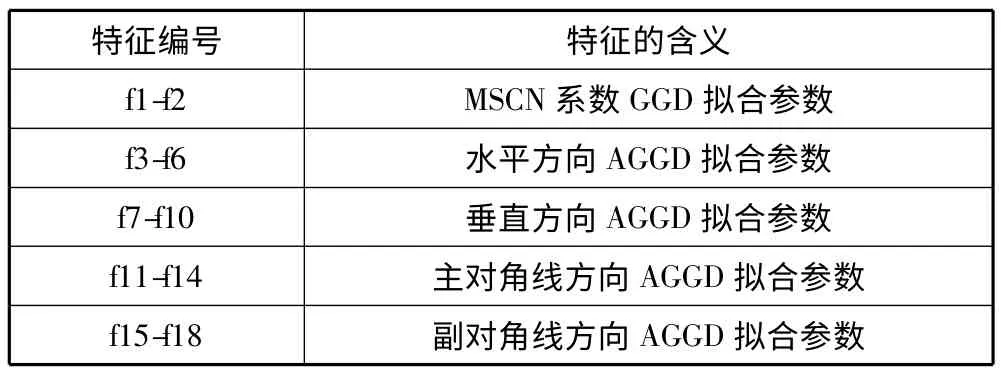
表1 提取的特征
1.4 MVG 模型建立与图像质量评价
上述步骤从自然图像中选定的兴趣区域图像分块计算得到了36 维的空域NSS 特征,通过式(12)MVG 密度函数来匹配这些特征,可以很好地表现这些特征的信息。

式(12)中(x1,...,xk)是计算得到的NSS 特征,ν 和Σ 代表了使用最大似然估计程序估算得到的MVG 模型的均值和协方差矩阵[17]。
通过对选取的一系列自然图像进行以上步骤最终得到自然图像的MVG 模型。前面提到本文算法是通过计算自然图像MVG 模型和测试图像MVG 模型的距离来评价图像质量的。
建立测试图像的MVG 模型跟建立自然图像的MVG 模型步骤相似,同样需要经过预处理、对图像分块、提取空域特征、建立MVG 模型等步骤。与建立自然图像MVG 模型不同的是,在建立测试图像MVG模型时没有引入兴趣区域选取的步骤,而是针对整幅图像建立MVG 模型的。具体原因是因为失真图像中不清晰就意味着失真的存在,如果忽视不清晰的图像分块,将会导致对失真严重程度的误判。而且失真的引入也会对兴趣区域的提取造成干扰,可能出现对于一幅失真严重的图像并不存在一个明显的兴趣区域的极端情况。
最终,失真图像的质量被表示为自然图像MVG模型和测试图像MVG 模型的距离,测试图像和自然图像MVG 模型距离的计算公式如式(13):
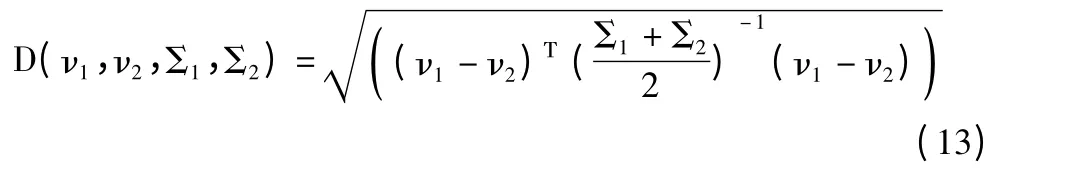
式(13)中ν1和ν2是自然图像MVG 模型和测试图像MVG 模型的均值向量,Σ1和Σ2是自然图像MVG 模型和测试图像MVG 模型的协方差矩阵。
2 实验结果和分析
本文使用LIVE IQA 图像数据库[18]来对本算法进行测试。LIVE IQA 图像数据库是由29 幅原始参考图像以及779 幅失真图像组成。失真图像是由原始参考图像通过不同类型的失真运算得到的,失真类型包括以下几种:JPEG2000 压缩失真、JPEG 压缩失真、白噪声、高斯模糊失真以及Fast-Fading 失真。LIVE IQA 图像数据库中的每一幅失真图像都提供有对应的DMOS(Difference Mean Opinion Scores)分值来代表该图像的主观评价分值,DMOS 分值范围为0到100,值越大代表图像主观评分越差,参考图像的DMOS 值为0。
为了对比客观评价算法的优劣,本文采用Spearman 等级次序相关系数(Spearman's Rank Ordered Correlation Coefficient,SROCC)和Pearson 线性相关系数(Pearson's Linear Correlation Coefficient,PLCC)来验证客观评价加过和主观评价结果直接紧密程度。计算得到的SROCC 与PLCC 两者的值越大,表示算法的性能越好。本文使用的SROCC 与PLCC 参数的计算公式如式(14)、式(15)所示:
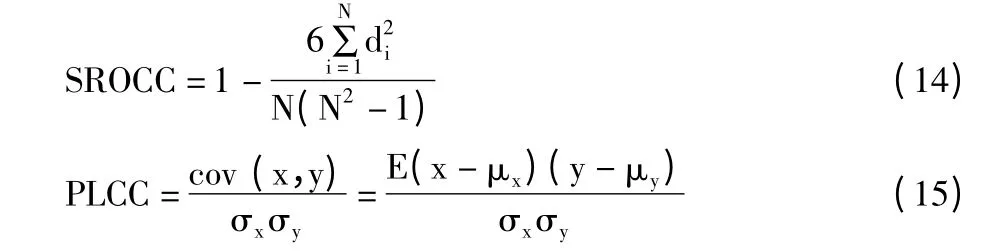
为了更好地测试本算法的性能,本文选取了全参考图像质量评价算法PSNR 与无参考图像质量评价算法NIQE[12]算法来与本算法进行比较,通过比较各算法的SROCC 和PLCC 评分来评价算法效果,并对实验结果进行比较。实验中计算过程重复多次,最终取多次实验结果的平均值作为实验的最终结果。具体结果如表2、表3 所示。
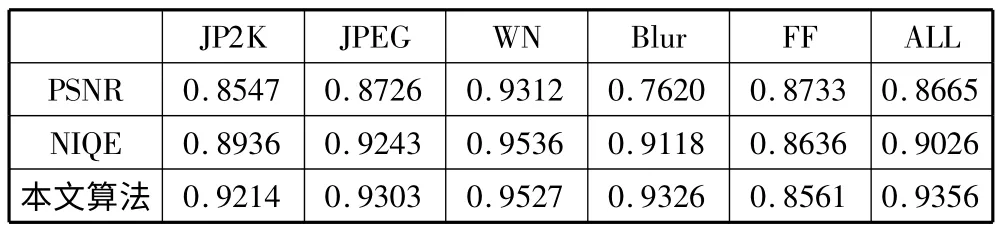
表2 实验SROCC 得分

表3 实验PLCC 得分
由上可知,对于全参考图像质量评价算法PSNR,本文提出的算法在JP2K 压缩、JPEG 压缩、白噪声、高斯模糊失真类型上的评价效果上全面优于全参考评价方法PSNR,在Fast-Fading 失真类型的评价效果差距不大,可以接受。由此可见本文算法较全参考图像质量评价算法有一定的优势。
对于无参考图像质量评价算法NIQE,通过上述表格可以看出,由于对兴趣区域的选取更加合理,本算法在JP2K 压缩、JPEG 压缩、白噪声、高斯模糊的失真类型与全类型失真的评价效果较NIQE 算法都有所提升,而在Fast-Fading 失真类型的评价结果差距较小,可以接受。
总体而言,本算法在NIQE 基础上加上了兴趣区域的选取,更好地提取了兴趣特征,故本算法优于PSNR 算法且较NIQE 算法效果有了一定的提升。
3 结束语
本文在经典的无参考图像质量评价算法NIQE的基础上进行了改进,利用空域自然场景统计特征,修改了原算法中自然图像MVG 模型建立过程中选择兴趣图像区块的算法为梯度密度的方法,提出了一种无需机器学习参与的无参考图像质量评价算法。该算法无需事先知道图像失真类型,也无需利用主观评分来训练,仅仅利用图像的自然场景统计特征来进行计算获得图像质量。实验证明,该算法与人类主观判断较为一致,跟NIQE 算法相比算法效果有所提升,且评价效果不逊色于当前主流无参考图像质量评价算法的效果。
本文提出的图像质量评价方法的思路也可以扩展到视频质量评价领域。在视频质量诊断领域,对应的方法为先提取出运动目标区域,作为视频帧的兴趣区域,然后基于提取的兴趣区域进行视频质量评价算法的设计,这样可以大大减少运算量,在实时性要求比较高的场景有很大的应用前景。
[1]高新波,路文.视觉信息质量评价方法[M].西安:西安电子科技大学出版社,2011:114-115.
[2]Lee A B,Pedersen K S,Mumford D.The nonlinear statistics of high-contrast patches in natural images[J].International Journal of Computer Vision,2003,54(1-3):83-103.
[3]Wang Z,Bovik A C,Evan B L.Blind measurement of blocking artifacts in images[C]// Proceedings of IEEE 2000 International Conference on Image Processing.2000,3:981-984.
[4]Narvekar N D,Karam L J.A no-reference image blur metric based on the cumulative probability of blur detection(CPBD)[J].IEEE Transactions on Image Processing,2011,20(9):2678-2683.
[5]Parvez Sazzad Z M,Kawayoke Y,Horita Y.No reference image quality assessment for JPEG2000 based on spatial features[J].Signal Processing:Image Communication,2008,23(4):257-268.
[6]Zhu X,Milanfar P.A no-reference sharpness metric sensitive to blur and noise[C]// IEEE 2009 International Workshop on Quality of Multimedia Experience(QoMEx).2009:64-69.
[7]Sheikh H R,Bovik A C,Cormack L.No-reference quality assessment using natural scene statistics:JPEG2000[J].IEEE Transactions on Image Processing,2005,14(11):1918-1927.
[8]Moorthy A K,Bovik A C.A two-step framework for constructing blind image quality indices[J].Signal Processing Letters,IEEE,2010,17(5):513-516.
[9]Moorthy A K,Bovik A C.Blind image quality assessment:From natural scene statistics to perceptual quality[J].IEEE Transactions on Image Processing,2011,20(12):3350-3364.
[10]Saad M A,Bovik A C,Charrier C.Blind image quality assessment:A natural scene statistics approach in the DCT domain[J].IEEE Transactions on Image Processing,2012,21(8):3339-3352.
[11]Mittal A,Moorthy A K,Bovik A C.No-reference image quality assessment in the spatial domain[J].IEEE Transactions on Image Processing,2012,21(12):4695-4708.
[12]Mittal A,Soundararajan R,Bovik A C.Making a“completely blind”image quality analyzer[J].Signal Processing Letters,IEEE,2013,20(3):209-212.
[13]Ruderman D L.The statistics of natural images[J].Network:Computation in Neural Systems,1994,5(4):517-548.
[14]Moorthy A K,Bovik A C.Statistics of natural image distortions[C]// IEEE 2010 International Conference on Acoustics Speech and Signal Processing(ICASSP),2010:962-965.
[15]Sharifi K,Leon-Garcia A.Estimation of shape parameter for generalized Gaussian distributions in subband decompositions of video[J].IEEE Transactions on Circuits and Systems for Video Technology,1995,5(1):52-56.
[16]Lasmar N E,Stitou Y,Berthoumieu Y.Multiscale skewed heavy tailed model for texture analysis[C]// IEEE 2009 the 16th IEEE International Conference on Image Processing(ICIP).2009:2281-2284.
[17]Bishop C M.Pattern Recognition and Machine Learning[M].New York:Springer,2006:200-202.
[18]Sheikh H R,Wang Z,Cormack L,et al.LIVEImage Quality Assessment Database Release 2[EB/OL].http://live.ece.utexas.edu/research/quality,2007-07-17.

