代价敏感相关向量机

苏乐群，冯爱民

(南京航空航天大学计算机科学与技术学院，江苏 南京 210016)

0 引言

传统的分类算法通常在假定样本均衡并具有相同的误分代价的基础上致力于提高分类器的泛化精度，但是在实际的数据挖掘问题中，不同的分类错误往往带来不同的损失，这种情况下应当致力于减少错误分类带来的代价而不是提高分类准确率［1］。在数据极端不平衡或者误分类代价存在很大差异的情况下，不考虑不同的样本误分类代价建立的分类模型是没有意义的。以当前出现的埃博拉病毒为例，明显将病毒感染者划分为健康人比将健康人划分为病毒感染者的代价高得多，此时分类精度并不能代表分类性能，因此将代价考虑进学习过程具有现实意义。

从1974 年Habbema［2］等人提出代价敏感问题开始，针对基于错误分类代价的代价敏感问题已经展开了大量的研究工作。目前代价敏感学习的方法主要分成2 大类:

1)重建训练集，然后使用现有的算法实现代价敏感学习，主要方法为重采样法，重采样方法是根据样本不同的误分类代价，增加高误分代价类训练样本的上采样和减少低误分代价类样本的下采样方法，代表算法有Boost 算法和Chawla［3］等人提出的SMOTE算法，由于在不平衡问题中更容易错分的是稀有类样本，Boost 算法(Schapire，1999)通过在每次迭代中添加错分样本使得分类器在下一次分类中更注重稀有样本达到对非平衡数据分类有良好的效果;SMOTE方法首先为每个稀有类样本随机选出几个邻近样本，并且在该样本与这些邻近的样本的连线上随机取点，生成无重复的新的稀有类样本，将原始不平衡的训练样本变得平衡，从而提高分类器对稀有类的识别率。随后Chawla 在2003 年提出SMOTEBoost 算法，它结合了SMOTE 和Boost 算法的优点，在每次迭代后为稀有类增加人工合成样本，实验表明该算法能够获得比原始2 种算法更好的性能，但都有着增加训练时间或损失样本信息的缺点。

2)重新设计分类器，包含阈值移动法和样本加权法，MetaCost［4］是一种典型的阈值移动方法，它利用了bagging 集成方法［5］来估计后验概率，然后使用阈值移动方法对训练集中的样本重新标记，最后在改变后的训练集上学习一个最小化错误率的分类器。样本加权法则是对不同类别中的样本被赋予不同的权值，使得高代价样本具有更大的权值，然后在带有权值的数据集上利用权值信息学习的方法训练一个以最小化错误率为目标的标准分类器，代价敏感支持向量机［6-9］也是基于这个思想实现的，此外Chen 等人在2005 年提出的支持向量修剪方法，针对不平衡数据通过改变2 类在软分类器中松弛变量前的系数来达到效果。

近年来许多学者在代价敏感问题上基于前人基础提出了一些更加优越的算法，如曹莹(2012)等人针对Boost、Adacost 等算法在不平衡问题中进行权值调整策略损坏了这些算法最重要的Boosting 特性提出了AsyB 与AsyBL［10］算法，通过对分类间隔的指数损失函数以及Logit 损失函数进行代价敏感改造，在理想情况下，优化这些损失函数最终收敛到代价敏感贝叶斯决策，通过实验证明了该2 种算法能够合理逼近最优代价敏感贝叶斯决策，使得错分类代价随着迭代的进行呈指数下降，最终得到具有更低错分类代价的代价敏感分类器。而在考虑到不同属性存在不同代价的情况，阮晓宏(2013)等人提出异构代价敏感决策树分类算法［11］，充分考虑了不同代价在分裂属性选择中的作用，构建了一种基于异构代价的分裂属性选择模型，设计了基于代价敏感的剪枝标准，避免了基于HCAl 分裂属性选择中的因属性信息特征值过小而被忽略的风险和误分类代价过大而被放大的可能，实验结果表明该方法在处理异构代价问题上能够获得稳健有效的性能。

2000 年，M.E.Tipping 提出一种稀疏概率模型即相关向量机(Relevance Vector Machines，RVM)［10］，它是在一种基于贝叶斯框架的稀疏学习模型。同支持向量机(SVM)相比，RVM 不仅具备由于运用自相关决策理论(Automatic Relevance Determination，ARD)获得的更强的稀疏性，而且具有极大地减少核函数的计算量、克服所选核函数必需满足Mercer 条件的缺点及更强的泛化能力等优点。

即使RVM 具有如此优越的性能，但同其它分类算法一样不具有代价敏感性，不能适用于代价敏感学习。为将性能优越的RVM 用以解决代价敏感问题，本文基于上述代价敏感性学习方法中的第二类方法的样本加权法，提出代价敏感相关向量分类算法(CSRVC)。

1 相关向量机

在模式分类中，相关向量机使用基于贝叶斯框架的稀疏学习模型，在先验参数的结构下基于自相关决策理论(ARD)来移除不相关的点，从而获得稀疏化的模型，具备着良好的稀疏性和泛化性能。

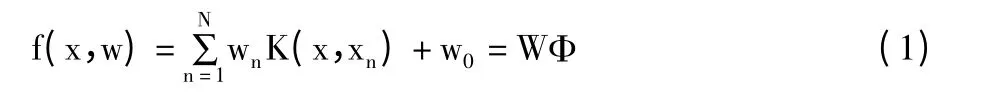
其中w=(w0，w1，w2，…，wn)，Φ=(1，φ1，φ2，…，φn)T为基函数，φn=K(x，xn)

RVM 核函数假设使用的是RBF 核函数:

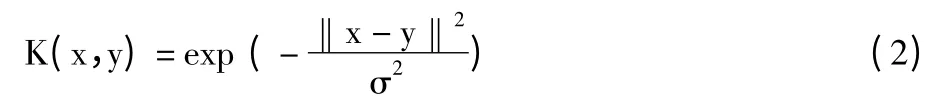
这里不要求基函数为正定的，因此核函数不必要满足Mercer 条件。

相关向量机［12］的分类模型就是计算输入属于期望类别的后验概率，实际上，相关向量机的分类模型将f(x，w)通过logistic Sigmoid 函数:

转换线性模型，则似然估计概率可写为(伯努利分布)［13］，假设样本独立同分布情况下，有:

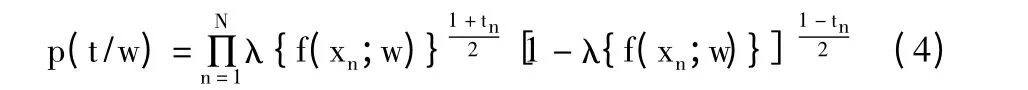
为了保证模型的稀疏性，相关向量机提出了通过在参数w 上定义受超参数α 控制的Gaussian 先验概率，在贝叶斯框架下进行机器学习，利用自相关决策理论(Automatic Relevance Determination，ARD)［14］来移除不相关的点，从而实现稀疏化。即假设权重向量w 的第i 个分量wi服从均值为0，方差为的Gaussian 分布。

定义权重的高斯先验:

其中α 为N+1 维参数。这样为每一个权值(或基函数)配置独立的超参数是稀疏贝叶斯模型最显著的特点，也是导致模型具有稀疏性的根本原因。由于这种先验概率分布是一种自动相关判定(Automatic Relevance Determination，ARD)先验分布，模型训练结束后，许多权值为0，与它对应的基函数将被删除，实现了模型的稀疏化。而非零权值的基函数所对应的样本向量被称为相关向量，这种学习机被称为相关向量机。

2 代价敏感相关向量分类

2.1 模型的提出

尽管标准RVM 是一种强大的模式分类算法，但它依然是基于精度的，不能直接用于代价敏感问题。鉴于不同样本的误分类具有不同的代价，本文把每类样本的不同误分类代价集成到RVM 的设计中，以最小化平均误分类代价为目的设计CS-RVC 算法。

假设样本的误分代价是基于类别的代价，即正类样本和负类样本的误分类代价不同，误分类代价只与类别有关。CS-RVC 通过样本加权方法在2 类样本上集成不同的代价敏感因子c+和c-，样本标记tn重新表示为:

由于不同误分类代价的引入，式(3)所表示RVM中使用λ(fn)和1 -λ(fn)来表示正确分类为正类和正确分类为负类的概率的Sigmoid 函数不能直接用于代价敏感问题。因此CS-RVC 使用了一种改进的Sigmoid 函数:

相应的误分类代价似然函数表示为:

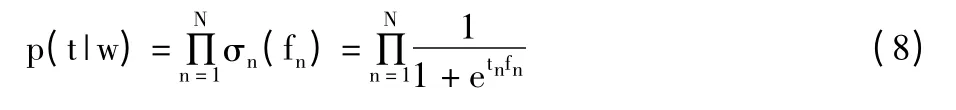
其中fn=f(xn，w)，求解最小误分类代价似然即为解决代价敏感分类问题的关键。

改进后的Sigmoid 函数可用性可用图1 来说明，虚线表示负类样本，y 轴左侧为负类面，同理实线表示正类样本，y 轴右侧围正类面，从图中可以看到当样本代价因子相同时，改进后的σ(y)与λ(y)等价适用到解决平衡分类问题，当负类的误分代价高于正类误分代价时，错误地分类负类样本将带来更高的误分代价，抑制了负类样本错误分类的概率，达到了代价敏感分类的目的。

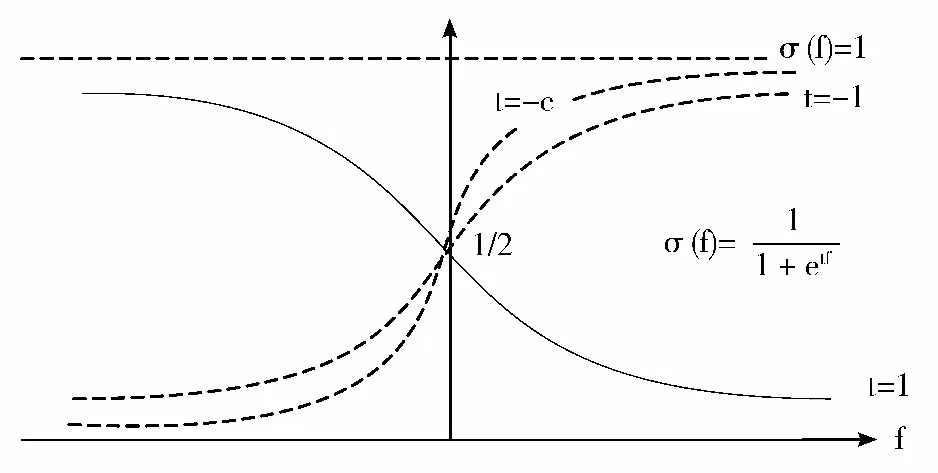
图1 改进Sigmoid 函数

利用自相关决策理论(ARD)，定义权重的高斯先验为:

根据贝叶斯理论推导出，w 的后验概率表示为:

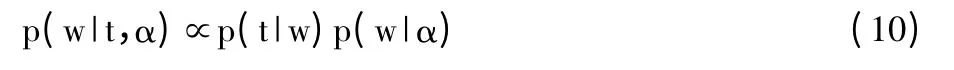
2.2 模型的求解

对w 和α 求解时，使用Mackay［15］提出的高斯二次逼近方法，当α 一定时，要找到最大后验概率值wMP，即要找到高斯近似分布的众数位置μMP，因此后验概率最大估计等同于:

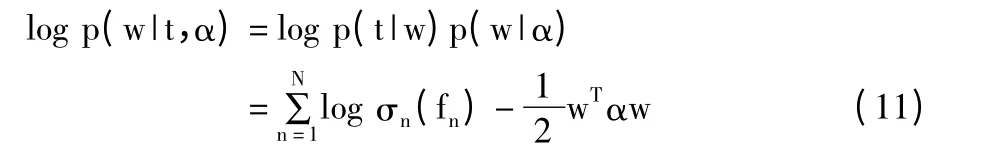
式中fn=f(xn，w)。

求得后验概率函数关于w 的梯度向量及海塞因(Hessian)矩阵:

式中A=diag(α1，α2，…，αn)。

通过牛顿方法(Newton’s Method)可以较快找到wMP，计算如下:

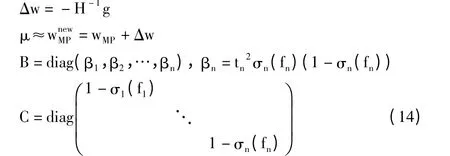
Gauss 正态分布来逼近后验概率分布的Laplace方法，是对后验概率分布的众数位置uMP处的函数的二次逼近。在IRLS 迭代收敛后，得到以权值向量μMP≈wMP为中心的近Gauss 分布，均值uMP，方差Σ=(ΦTBΦ+A)-1。

同样地，使用Laplace 逼近方法可以将边缘似然函数近似表示为:

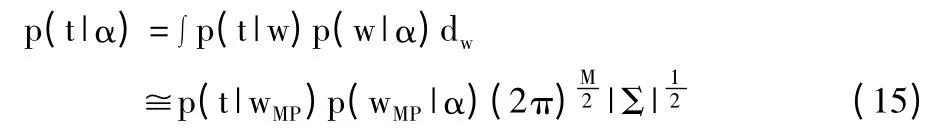
近似的边缘似然函数对数的形式为:

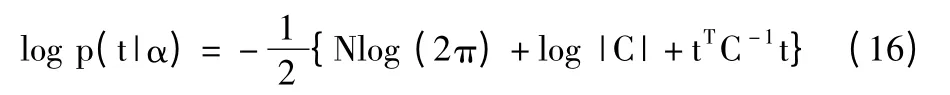
式中C=B+ΦA-1ΦT

2.3 超参数优化

将权重向量w 看作成一个隐藏变量，用EM 算法［16］来估计超参数α 的值，表达为:

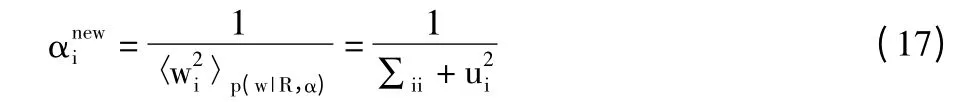
直接对式(15)求偏导有:

式中，μi=0 是后验概率p(w|R，α)的均值向量μ 的第i 个后验概率，Σii是后验概率，p(w|R，α)的方差Σ的第i 个对角元素。

2.4 模型求解步骤

模型的求解步骤如图2 所示。

图2 模型的求解步骤

3 实 验

3.1 二维人工数据实验

为观察相关向量分类算法(RVC)和代价敏感相关向量分类算法(CS-RVC)分类边界的位置，在随机生成的二维样本上实验。设类1 样本的误分代价为1，类2 的误分类代价为5，代价矩阵如表1 所示，使用高斯核函数，高斯核带宽参数width 搜索范围取2t，其中t∈{-2，-1，0，1，2}，搜索步长为1。

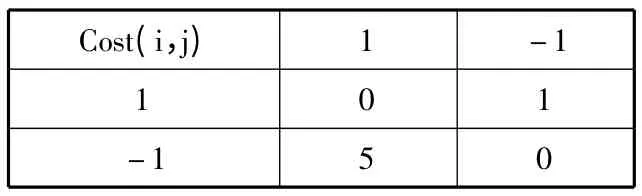
表1 代价矩阵

从表2 中可以很清晰地看到核带宽参数的选择对代价敏感分类带来的影响，选择一个合适核带宽同样显得很为重要。通过查资料可知SVM 的稀疏性为20%左右，由此可以看到CS-RVC 优越的稀疏性。

表2 核带宽参数选择对RVC 与CS—RVC 的分类性能影响

由图3 可以清晰地看到，相对于RVC 而言，CSRVC 的分类边界明显趋向于尽量分对误分类代价高的2 类样本，尽管分类精度下降，但是分类代价较高的类2 样本的分类正确率明显提高，使误分类的代价大大降低。

3.2 UCI 数据集实验

实验使用了2 个UCI 数据集Heart Disease 和German Credit，2 个数据集的符号属性转化成整型，Heart 数据集中标记为‘健康人’的样本为正例，‘病人’和‘欺诈’为负例，Heart 数据集包含139 个正例与164 个负例。German 数据集中包含300 正例和700 负例，2 个数据集的代价矩阵同为图3 所示，在每个数据集上取10 次实验的平均值，每次递增的选择一定数目的样本组成训练集，其余样本为测试集，图4 和图5 为实验结果。

如图4 中所示的RVC 和CS-RVC 在2 个UCI 数据集上的平均误分类代价，可以很清晰的看到由于引入了代价敏感因子使得CS-RVC 比RVC 相比有着小得多的平均分类代价，实现了代价敏感挖掘。

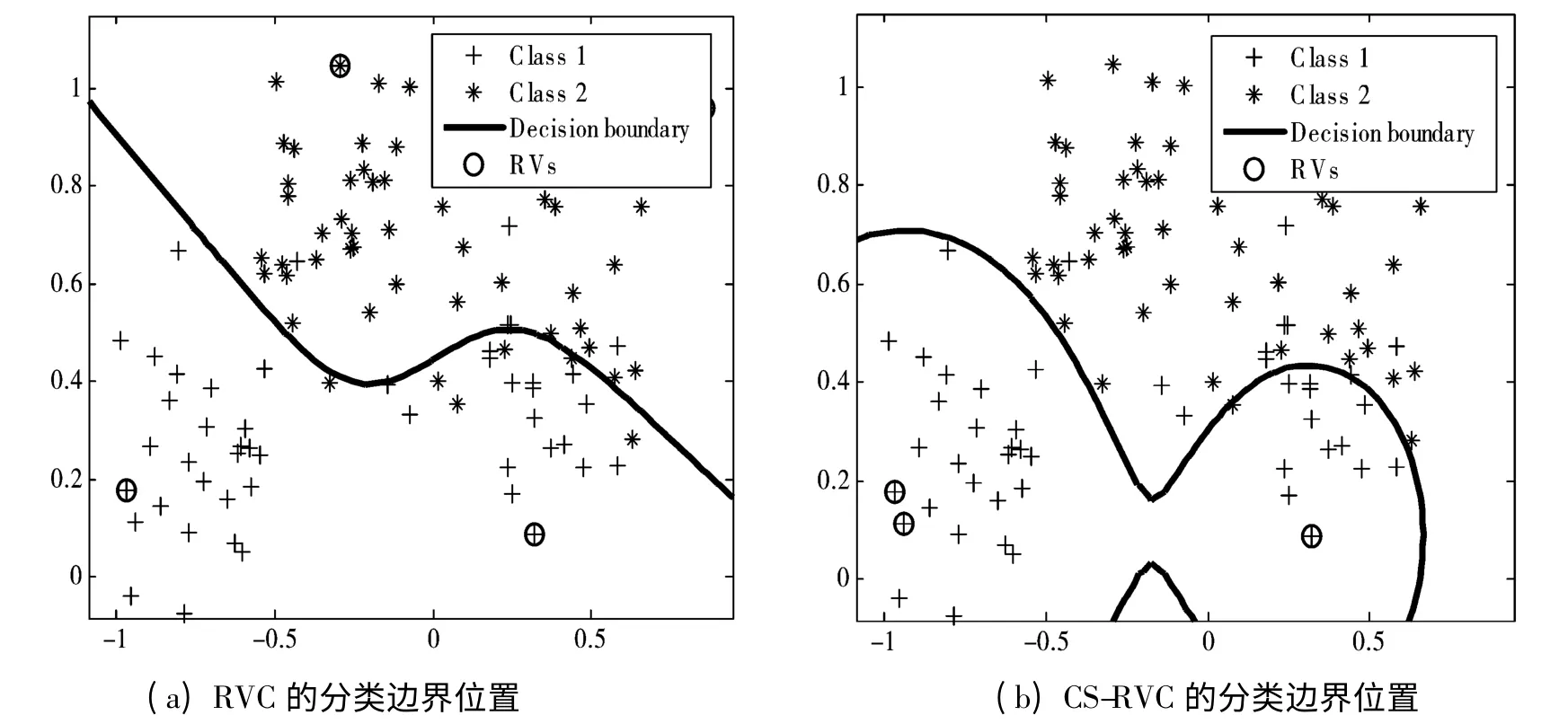
图3 随机样本上的分类超平面

图4 RVC 和CS-RVC 测试集上平均误分类代价

图5 RVC 和CS-RVC 在测试集上的分类性能

与RVC 相比，虽然CS-RVC 获得了更小的平均误分类代价，为了考证它们在分类错误率上的比较，图5 给出了基于不同尺度训练集(每个训练集在原样本集上随机采样得到)的CS—RVC 和RVC 的分类准确率，TP—RVC、TN—RVC 和AC—RVC 分别表示基于RVC 的正例分类精度(正确分类正例数/正例数)、反例分类精度和全局精度.TP—CS—RVC、TN—CS—RVC 与AC—CS—RVC 分别表示基于CS—RVC的正例、反例分类精度和全局精度。从中可见，AC—CS—RVC 低于AC—RVC，即CS—RVC 较于RVC 误差率有所提高，但在误分类代价较高的正例样本上获得较高的分类精度，在误分类代价较低的反例样本上获得相对低的分类精度，符合了代价敏感挖掘的需求。

4 结束语

当样本的误分类代价不相等时，传统的基于分类精度的分类器不能满足数据挖掘中最小化错误分类代价的需求。通过将代价敏感的思想集成于相关向量分类器上，使用样本加权方法使得误分类代价较高的样本具有较大的分类错误代价，提出代价敏感相关向量机的设计方法。它具有相关向量机基于稀疏概率模型下强大的稀疏性及泛化能力和最小化平均误分类代价2 个优点。

二维人工数据实验和UCI 数据实验共同验证了CS-RVC 良好的稀疏性和分类性能，当每类样本的误分类代价不相等时，和RVC 相比，虽然CS—RVC 损失了一部分的全局分类精度，但由于提高了误分代价较高的样本的正确分类率，使得分类超平面偏向于误分代价较小的样本簇，大大降低了平均误分类代价。很好地实现了代价敏感的数据挖掘。

对于CS—RVC，虽然其取得了较低的平均误分类代价，但损失的分类精度也比较高，设计一个兼顾分类精度与平均误分类代价的算法是很有意义的进一步研究工作。

［1］叶志飞，文益民，吕宝粮.不平衡分类问题研究综述［J］.智能系统学报，2009，4(2):148-156.

［2］Habbema J D F，Hermans J，Van Der Burgt A T.Cases of doubt in allocation problems［J］.Biometrika，1974，61(2):313-324.

［3］Chawla N V，Bowyer K W，Hall L O，et al.SMOTE:Synthetic minority over-sampling technique［J］.Journal of Artificial Intelligence Research，2002，16:321-357.

［4］Domingos P Metacost.A general method for making classi-fiers cost-sensitive［C］// Proceedings of the fifth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.ACM，1999:155-164.

［5］Breiman L.Bagging predictors［J］.MachineLearning，1996，24(2):123-140.

［6］Brefeld U，Geibel P，Wysotzki F.Support vector machines with example dependent costs［M］// Machine Learning:ECML 2003.Springer Berlin Heidelberg，2003:23-34.

［7］刘胥影，姜远，周志华.类别不平衡性对代价敏感学习的影响［C］// 人工智能学会第12 届学术年会，中国人工智能进展.2007:45-50.

［8］郑恩辉，李平，宋执环.代价敏感支持向量机［J］.控制与决策，2006，21(4):473-476.

［9］Fumera G，Roli F.Cost-sensitive learning in support vector machines［C］// Workshop on Machine Learning，Methods and Applications，Held in the Context of the 8th Meeting of the Italian Association of Artificial Intelligence.2002.

［10］曹莹，苗启广，刘家辰，等.具有Fisher 一致性的代价敏感Boosting 算法［J］.软件学报，2013，24(11):2584-2596.

［11］阮晓宏，黄小猛，袁鼎荣，等.基于异构代价敏感决策树的分类器算法［J］.计算机科学，2013，40(11A):140-142.

［12］Bishop C M，Tipping M E.Variational relevance vector machines［C］// Proceedings of the Sixteenth Conference on Uncertainty in Artificial Intelligence.2000:46-53.

［13］Vapnik V N，Vapnik V.StatisticalLearning Theory［M］.New York:Wiley，1998.

［14］Li Y，Campbell C，Tipping M.Bayesian automatic relevance determination algorithms for classifying gene expression data［J］.Bioinformatics，2002，18(10):1332-1339.

［15］Mackay D.The evidence framework applied to classification networks［J］.Neural Computation，1992，4(5):720-736

［16］Thayananthan A.Relevance Vector Machine based Mixture of Experts［D］.Department of Engineering，University of Cambridge，2005.

［17］Platt J C.Probabilistic outputs for support vector machines and comparisons to regularized likelihood methods［M］//Advances in Large Margin Classifiers.MIT Press，1999:61-74.

［18］Chen H，Tino P，Yao X.Probabilistic classification vector machines［J］.IEEE Transactions on Neural Networks，2009，20(6):901-914.

［19］Han J，Kamber M.Data Mining，Southeast Asia Edition:Concepts and Techniques［M］.Morgan Kaufmann，2006.

［20］周志华.普适机器学习［EB/OL］.http://wenku.baidu.com/link?url=ZhAh423i0RLQfcCUKaTPk0ojoV5765Zu-7O0vWxCkLlgjF8YmJGzmNKkoiP1hjhD6zeOmXvmaag0we-MRwHbbPYHBEAlVooCRLBfeL3EVhDa，2014-11-12.