规整填料表面液体分布的计算流体力学

谭丽媛，袁希钢，KALBASSI Mohammad Ali



规整填料表面液体分布的计算流体力学

谭丽媛1，袁希钢1，KALBASSI Mohammad Ali2

（1天津大学化学工程联合国家重点实验室，天津 300072；2Air Products Public Limited Company，Walton on Thames，UK）

采用计算流体力学（computational fluid dynamics，CFD）中的VOF方法对规整填料表面液相分布进行了三维建模和仿真，实现规整填料内液相分布的可视化并得到了液膜厚度和有效相界面积比等相关定量信息。通过分析比较不同物系的数值模拟结果，发现液体的表面张力和黏度都对填料表面上液体分布有影响。表面张力越小，液相在填料片上分布越均匀，有效相界面积比越大，液膜厚度越小；黏度增加，有效相界面积比和液膜厚度也随之增加。较之于黏度对液相分布的影响程度，表面张力的影响程度更大，为主要影响因素。本文还提出一个预测有效相界面积比的新公式，并将数值模拟结果与已有文献进行对比，吻合性较好。

计算流体力学；可视化；液膜厚度；有效相界面积比；表面张力；黏度

规整填料塔因在汽提和吸收过程中为气液两相提供有效的接触面而被广泛应用于工业生产中，其分离效率的预测和提高一直以来都是研究人员最为关注的问题。Mohamed等[1]在对气液相在规整填料塔内分布的研究中发现，液体在规整填料塔内的不均匀性分布是影响塔分离效率的决定性因素，而气相即使是在初始时就分布不均匀，也不会对塔的分离效率有影响。因此规整填料表面液相分布的研究在规整填料基础研究中占有重要地位。液体在小尺度区域（基本结构单元）内的流动会在很大程度上影响液体在宏观尺度上的分布。在一个结构单元内，液体的分布是由液体流过填料波纹波峰、填料节点和填料表面的孔洞所决定的。然而对结构单元内液体流动分布的定量特征和平均液膜厚度的研究却鲜有研究报道[2]。

早期对规整填料内液体宏观流动分布的研究模型多为基于实验研究提出的经验或半经验理论模型，如针对板波纹填料提出的SRP模型[3-6]、基于规整填料波纹几何形状Olujic等[7-8]提出的Delft模型、徐崇嗣等[9]通过对Dangizer[10]提出的静态混合器中液体分布模型进行分析研究而建立的节点网格模型。针对规整填料内液体的微观流动，如规整填料表面液膜流动，Nusselt[11]是最早对液膜流动进行研究的学者之一，他提出的降膜理论到现在仍可用于估算规整填料内的平均液膜厚度。Shetty和Cerro[12-13]最早提出了用于规整填料塔设计的一套完整的液膜流动模型。虽然液膜流动模型是以表面带有波纹的规整填料为研究背景，但与实际填料上的液膜流动情况仍有很大差距。谷芳[14]、陈江波[15]采用LDV技术对规整填料表面液相流动分布进行了测试分析。

最近几年，随着计算流体力学（computational fluid dynamics，CFD）和相关学科的发展及其能有效地简化实验设备和减少相关设备成本，CFD已成为研究复杂模型中多相流必不可少的工具[16-17]。另外，采用实验的方法不能对填料塔内的流体力学参数提供详细的信息，也很难利用探针测量规整填料塔内下降液膜的速度、温度和压力分布，这也使得数值模拟在这方面更加重要[18]。

受目前计算能力的限制，对整个填料塔内每一现象（流体动力学、传质、化学反应）进行模拟是非常困难的。因此，对规整填料塔的数值模拟研究主要从3个不同的尺寸：微尺度、中尺度和宏观尺度[19-20]进行研究分析。微尺度的模拟通常是毫米或者厘米尺寸的，计算域网格大小是微米级的。Szulczewska等[21]基于Mellapak 250.Y型板波纹规整填料建立一个二维两相流CFD模型，模拟了规整填料简化模型上气液两相逆流流动过程。二维模拟不仅可以大大简化数值模拟方法和显著减少计算量，当液相以完全膜状流进行流动时，二维模拟还可以对其流体动力学参数给出很好的近似。但随着液体流率的减小，表面张力的作用会使液体流动由溪流变为滴流，这些行为均为三维结构，无法使用二维模拟进行模拟观察[22]。Iso等[23-24]对倾斜板上液膜流动进行了三维CFD模拟，很好地观察了液体的溪流和滴流等行为。对于微尺度，液体的不均匀分布流体动力学是影响规整填料塔性能的关键因素，对其进行研究是很有必要的。中尺度的研究包含气、液相在金属规整填料内的流动，可以给出填料塔的干板压降等流体力学参数。在研究过程中，可以用规整填料一系列的特征单元代表整个填料。Hosseini等[25]利用不同的湍流模型研究了气液两相在Mellapak Plus 752.Y规整填料上的流体力学特性。Haroun等[26]对具有不同接触角的液体在Mellapak 250.Y规整填料特征单元上液相流动分布情况进行了三维数值模拟，并对其有效相界面积和持液量进行了预测。Shojaee等[27]利用VOF模型研究了Gempak2A规整填料特征单元上液相流动分布及气、液相流率对有效相界面积的影响。Dai等[28-29]采用CFD中欧拉多相流模型对规整催化填料结构与其压降和传质系数的关系进行了三维数值模拟，并通过优化规整催化填料的结构参数提高其传质系数和降低压降；之后又利用此模型对泡点反应器中苯与丙烯烷基化反应进行了模拟，确定了规整催化填料的最佳操作条件。宏观尺度利用从中尺度研究得到的相关关联式作为输入，进而决定填料塔内的流型以及壁面、分布器等对其影响。Raynal等[19]运用从全规模反应中尺度下得到的压降关联式检查3种不同几何构型的速度模型：无气相分布器、垂直管分布器、冲击板垂直分布器；最后用多孔介质模型模拟全塔，并得到较好的结果。

综上所述，早期对规整填料塔内流动的研究主要集中在宏观流动分布方面，目前则集中在填料内部及更小尺度的流动描述，而且采用CFD方法研究填料内部的流动成为一种趋势。虽然已有文献针对不同尺度的液相不均匀分布的流体动力学进行研究，但是这两者之间的特点仍需要在微尺度方面进行全面的理解。本文致力于研究液相物性对液体在填料表面分布的影响，建立了基于VOF方法的三维CFD数值分析模型。在研究过程中，作者首先对不同表面张力和黏度的物系在规整填料简化模型上的分布进行分析研究，在此基础之上，对液体在Mellapak 500.Y规整填料的近似结构单元上的分布进行模拟研究。

1 数值模拟模型

1.1 物理模型

基于规整填料的结构特点，倾斜平板（或波纹板）被认为是规整填料片的最简化单元。研究液体表面张力和黏度对液体在倾斜板上的分布是后续研究液体在规整填料更复杂模型上分布的一个重要步骤。

本文所采用的倾斜波纹板的计算模型如图1所示，该物理模型和流动条件的设置是基于现有倾斜板上液体流动分布研究[22-24]来设定的。物理模型尺寸为60mm×50mm×7mm，板上小波纹间距= 2.8mm，波峰=0.3mm，波纹倾角=60°。由于液相雷诺数较低（<300），液体在波纹板上流动方式视为层流，利用Nusselt液膜理论[11]估算液相进口区域为50mm×0.4mm。模拟计算过程中液相进口边界条件取为速度进口 Velocity-inlet，L=0.3m/s；左右两边侧壁和波纹板为不锈钢材质且边界条件取无滑移壁面；出口边界条件取为压力出口Pressure- outlet，出口压力为0。为确定波动液膜的自由表面位置，采用结构化网格划分该模型，并对近壁面区域进行网格加密，同时选用带有几何重建格式的VOF模型进行相界面的追踪和捕获。

精馏塔规整填料通常为波纹板或者丝网结构。在填料塔中，规整填料被排成较塔内截面略小的圆盘[图2(a)]），一盘之内，左右相邻两片规整填料的波纹倾斜方向相反。金属板波纹填料上波纹与长边的斜角为45°或60°，板片上打出一些小孔以利于气体穿过[图2(b)]。为减少计算时间，对规整填料结构单元进行一定的简化，规整填料片表面上没有开孔，三维CFD数值模型如图2(c)所示。模型上方即(1)设为液相速度进口（velocity-inlet）边界条件，L=0.01m/s；模型下方即(2)设为压力出口（pressure-outlet）边界条件，出口压力为0；前后两片填料为不锈钢材质即(3)设为无滑移壁面 (wall)；为了保证液体流动的连续性，模型左右两边即(4)有一定的液相流入，可近似为周期性边界条件。规整填料的结构尺寸=10.10mm，波高=6.52mm。由于规整填料物理模型结构较为复杂，采用非结构化网格对其进行划分，近壁面处进行网格加密，选用带有几何重建格式的VOF模型进行气液相界面的追踪和捕获。

1.2 数学模型

本文采用的数值模拟方法是基于Hirt等[30]提出的适用于追踪两非混相界面的VOF方法。在流体动力学模型中，利用数值求解质量守恒和动量守恒。质量守恒可导出连续性方程，动量守恒可导出Navier-Stokes方程，即连续性方程如式（1）。

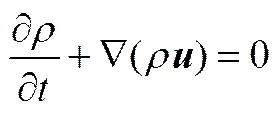
Navier-Stokes方程如式（2）。

（2）

式中、、、和为局部的速度、密度、压力、黏度和重力加速度；为除压力、黏性力和重力之外的作用于流体上的其他力，本文中取表面张力。在研究过程中，采用Brackbill等[31]提出的连续表面力（continuum surface force，CSF）模型，使得表面张力在动量方程中以源相的形式加入到VOF的计算中，如式（3）。

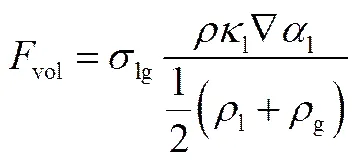
式中，l为网格单元内的液相体积分数，0

（4）

为表面张力系数，为自由表面曲率，其定义式如式（5）。

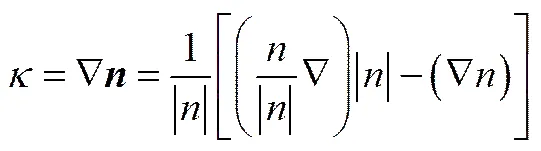
（6）

式中，、w为壁面处的单位法向量和切向量；w为壁面处界面切线与壁面的夹角。液相与壁面之间的接触角及液相的表面张力利用OCA15EC光学接触角测量仪测量得到。

无论是对气相还是液相，每一相的体积分数都遵从该相的转运方程，如式（7）。

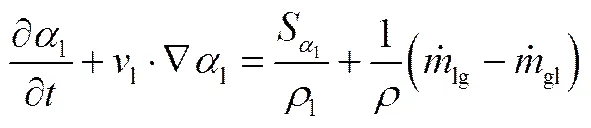
（8）

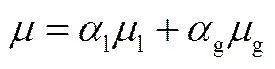
1.3 数值模拟策略

本文主要考察液相在规整表面及其简化模型上的分布及液体物性对其分布的影响情况。为了简化数值模拟计算的时间，在模拟过程中假定气相在填料内没有流动，液体的流动方式为层流。即气体速度为零，对液体的流动没有影响。已有的研究表 明[14，27]，载点以下气相对液相的影响作用很小，因此在模拟过程中假定气相为停滞相是合理的。为模拟填料表面瞬态气液两相流体动力学特性，VOF模型采用显示差分格式，采用界面重构方法（geo-reconstruct method）作为体积分数离散格式，二阶迎风格式求解动量方程，压力项选用PRESTO！算法，压力-速度耦合方程的求算采用PISO格式。计算过程中，压力项的松弛因子为0.3，动量项为0.45，若连续性方程的残差降至1×10-4以下，各个方向速度的残差降至1×10-5时，可认为方程已收敛。模型计算推进时间步长Δ取1×10-5s，确保能准确模拟研究工况速度范围内气液两相流体动力学特性。壁面为无滑移壁面，给定液相与壁面之间的接触角。模拟计算初始时气相充满整个模型，即气相的体积分数g=1，l=0。经网格独立性验证后，倾斜波纹板的网格数为233840，规整填料片的网格数为638935。

1.4 模拟物系

本文主要考察液体物性如黏度、表面张力等对液体在波纹规整填料片上的分布及润湿情况的影响。表1列出了模拟物系的物理性质。

表1 模拟物系的物性

2 模型验证

为了验证该计算模型和方法的准确性，按照文献[23-24]中的模拟条件对进行了相应的模拟计算，对比了在相同情况下液相在倾斜波纹板面上的流动分布情况。图3为两种模拟结果的对比，二者吻合很好，证明了该数值模型和计算方法的准确性。

3 液相在倾斜波纹板上的分布

3.1 液相物性对液相流型的影响

图4给出了以平行于波纹板的视角液体在倾斜波纹板上的分布情况，颜色的深浅表征液膜厚度的大小。以液体在倾斜波纹板上的润湿面积比率来考察液相在倾斜波纹板上的润湿情况，润湿面积比率为液相在板面上的润湿面积w与板的总面积t的比值，如式（10）。

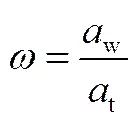
式中，润湿面积的是根据Lan等[32]的研究，以l=0.5处为气液相界面，利用CFD-post软件对其进行积分得到。若表示液相在板上的流型为溪流或滴流，表示液相在板上以完全膜状进行 流动。

数为表面张力和惯性力的比值，用数来表征液体流型的变化可以反映出表面张力对液相分布的影响。从图4可以看出，表面张力较低的液体（如乙醇、丙酮）在倾斜波纹板上以完全膜状流进行流动，润湿面积达到最大。在相同流率下，随着表面张力的增加，液相在板上的润湿面积逐渐减小，开始以溪流形式进行流动。另外可以明显地看到溪流液膜表面呈现一定的波动，在液膜积聚处有明显的突起，随后液体又在板上有一定的分散。对于表面张力相当的物系，如甘油和水以不同体积比混合的溶液，随黏度增加，润湿面积也逐渐增大。

3.2 计算润湿面积新模型

为了更好地描述表面张力和黏度对液相在倾斜波纹板上分布的影响及其影响程度，在对不同液相物系在规整填料片上的润湿面积的计算和分析基础上，猜想液相的表面张力和黏度对液相在倾斜波纹板上的润湿面积的影响可以用式（11）进行表述。

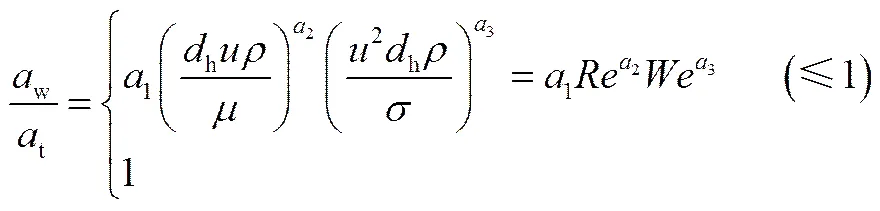
为了确定参数1、2、3的具体数值，又对不同表面张力、不同黏度的物系在不同流量在倾斜波纹板上的润湿情况进行了数值模拟，最后利用Matlab数学软件进行多元非线性最小二乘法拟合，得到各个参数的具体数值，如式（12）。

（12）

图5为数值模拟实验数据点与CFD关联式（12）之间的关系图，计算误差在8%以内，二者吻合性较好，该模型可以很好地预测液体在倾斜波纹板上的润湿情况。从作者课题组提出的这个计算润湿面积新模型中可以看到，液体表面张力和黏度对液相在倾斜波纹板上润湿面积的影响是相反的，润湿面积随表面张力增加而减小，随黏度的增加而有微量的增加，但表面张力的影响作用要远大于黏度对润湿面积的影响。

3.3 倾斜波纹板上的液膜厚度

作为液体流动特性重要流体力学参数之一的液膜厚度，需要对其进行详细的研究。为了避免液相进口对模拟结果的影响，以距液相进口5mm处的水平面为基准，考察液相物性对液膜厚度的影响。图6给出了在此水平面上两组黏度相近但表面张力相差较大的物系之间液膜厚度的比较关系。从图6中可以看到，低黏度物系组，即低表面张力物系（乙醇）的液膜厚度与高表面张力物系（水）的液膜厚度之间的差值大于高黏度物系组液膜厚度的差值。可以说在相同流量下以膜状流进行流动时，表面张力的增加可以使液膜厚度有微小的增加，但增量不大；在图6中还可以看到，在壁面附近即图的左右两侧，受到壁面的影响，液膜厚度急剧增加且远大于在波纹板面上流动的液膜厚度。因此在工业生产中要尽量避免壁流现象的出现，这会使传质、传热效率在很大程度上降低。

图7给出了在同一水平面上两组表面张力相近但液相黏度相差较大的物系之间液膜厚度的比较关系。从图7可以看出，两组物系的液膜厚度均随液相黏度的增加而增加，但低表面张力物系组液膜厚度增加的幅值小于高表面张力物系组液膜厚度增加的幅值。可以说，对高表面张力物系，液相黏度越大，液膜厚度越大。

为了进一步考察完全膜状流在沿倾斜波纹板流动过程中液膜厚度的变化情况，给出在完全膜状流宽度中间位置处的乙醇和丙酮的液相体积分数云图以及液膜自由表面、液膜厚度沿波纹板流动方向的变化，如图8所示。从图8(a)、8(b)两个图中可以看出，液膜自由表面波动趋势和波纹壁面上的波纹变化几乎完全重合，即黏度和重力对液膜的流动结构没有影响，这一数值模拟结果与谷芳[14][谷芳, 2004 #33]二维模拟的结果一致，可以说液相只有在板面上以完全膜状流流动时，三维流动模型才可以简化为二维模型。图8(c)为膜状流在沿倾斜波纹板流动过程中液膜厚度的变化情况，受波纹壁面的影响，液膜厚度并不是保持不变的，而是呈现一定的波动性。最大液膜厚度出现在波谷处（即有一定的积液现象），在波峰处液膜厚度最小，且这种不对称性随着黏度的增加而增加。

综上，根据倾斜波纹板上液相分布情况的分析研究可知，表面张力和黏度都对液相在倾斜波纹板表面上的分布有影响，表面张力越小，液相在倾斜波纹板片上分布越均匀，润湿面积越大，液膜宽度越大，液膜厚度越小；随黏度的增加，有效相界面积和液膜厚度均增加，但表面张力的影响程度大于黏度的影响程度，为主要影响因素。为此，在研究规整填料片上液相分布影响因素时，作者重点考察了表面张力对其的影响。数值模拟过程中取空气和水为气液两相流，仅改变水的表面张力，其他物性保持不变，根据Elioni等[33]对液相在规整填料片上接触角的影响的研究结果，估算了不同表面张力的水在规整填料片上的接触角。

4 表面张力对液相在规整填料片上分布的影响

4.1 液相在规整填料片表面上的分布

图9给出了具有不同表面张力的流体在规整填料片上的流动分布情况，颜色的深浅不仅可以表征流体体积分数的大小，也可以表征液膜厚度的大小。从图9中可以看到，表面张力越低，液体在规整填料表面分布的越均匀；随着表面张力的逐渐增加，液相在规整填料片上的流动分布越来越不均匀，沟流现象越来越明显且对称性分布也越明显。另外从图9中可以很明显地观察到，在规整填料波纹的波峰相交处即填料节点处有一定的滞液，液相流股在此节点处混合而后进行再分配，使得液体从波纹板的一个通道流入相邻通道。为了避免节点处的积液，在安装填料的时候可以使相邻填料片间隔1～2mm，而对于高比表面张力的物系，可以在不改变液相其他物性的前提下加入一定量的表面活性剂，从而使其在填料内的分布更加均匀，以达到强化传质的效果。

4.2 液相在规整填料内的有效面积

就规整填料塔而言，有效面积e一般指单位填料体积内液相的相界面积，是影响传质过程的最重要因素。规整填料塔内的有效相界面积可以通过物理方法，如电阻法、光传导以及反射技术测量得到，但在多数情况下，规整填料塔内有效相界面积是通过控制快速反应的吸收过程计算测量得到的。Billet等[34]通过整理已有文献中测量填料塔内润湿面积的实验数据，归纳得出一个适用于求解所有气液两相逆流操作的填料塔内的有效相界面积公式，如式（13）。

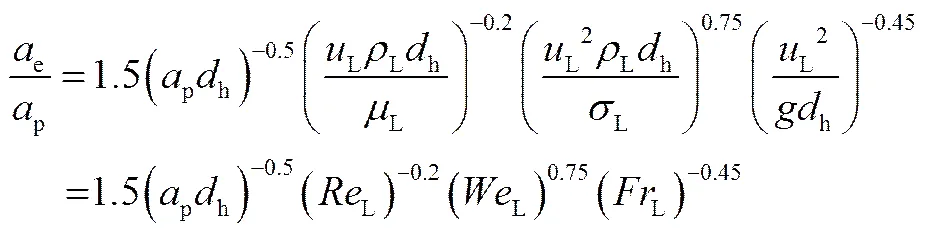
Olujic等[35]通过将Onda模型[36]和Delft模型进行合并，得到一个对求解大比表面积，特别是波纹倾角为60°的规整填料有效相界面积更加有效的公式，如式（14）。

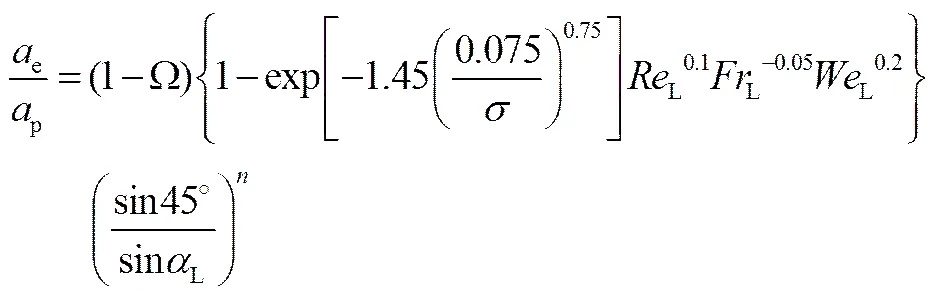
式中

（15）

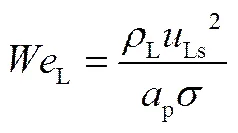
（17）

为填料表面上孔的面积占填料比表面积的比值，对Mellapak型填料，。L为液相在规整填料内的有效流动角度，如式（18）。

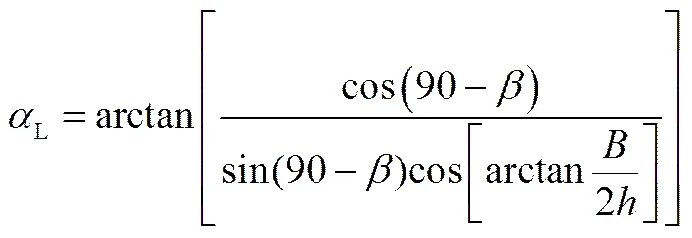
式中，为填料的波纹倾角；为填料两波峰之间的宽度；为填料波纹峰高。以常见的比表面积为250m2/m3，波纹角度为45°的填料和大气压作为参考点，指数的计算如式（19）。

（19）

本文的研究中，CFD数值模拟求解得到的有效面积与Billet等[34]和Olujic等[35]的求解方式是不相同的。在数值模拟过程中，利用CFD-post后处理软件对液相体积分数进行积分得到有效相界面积。图10给出了液相在规整填料内的有效相界面积随表面张力的变化情况，并将数值模拟结果与已有经验公式进行了对比。随着表面张力的增加，液相在规整填料内的有效面积逐渐减小。表面张力较低时，CFD数值模拟结果与Olujic经验公式[35]较为一致，随表面张力的增加，二者的差值逐渐增加。这主要是由于一方面Olujic模型[35]中考虑了填料表面穿孔的影响，而该数值模拟的物理模型表面没有穿孔。规整填料表面穿孔不仅有利于液相从一个流道向另一个流道流动，而且有助于形成液滴，增加有效面积。在本次模拟过程中，没有发现有液滴的生成。另一方面，Olujic模型[35]的推导是在Onda等[36]散堆填料模型的基础上利用有机物所做实验得出的结果，而有机物的表面张力普遍较低，因此Olujic模型更适用于表面张力较低的物系。当液体具有较高表面张力时，CFD数值模拟结果与Billet模型[34]的预测结果吻合很好，而Billet模型所采用的实验数据中液相的表面张力较高，可以说Billet模型适用于液相表面张力较高的物系。因此，当利用经验公式来预测规整填料塔内有效相界面积时，要根据液相的具体物性选用合适的经验公式。模拟的结果说明利用CFD数值模拟不仅可以使液相在规整填料片上的分布可视化，还能够准确反应预测液相物性对液相在规整填料片上分布的影响和有效相界面积值，不受经验公式适应条件的限制。

4.3 规整填料片上液膜厚度

观察液相在规整填料片上的分布，不难发现液相在规整填料片上的液膜厚度并不像倾斜波纹板上均匀。在填料节点处，由于液相的积聚和再分配，使得液膜呈现一定的周期性分布且在节点附近液膜厚度最大；液膜厚度在径向和轴向上的分布也都非常不均匀，因此，利用平均液膜厚度来代替局部液膜厚度具有更大的实用价值。研究填料塔的流体力学性能时，虽然可以通过一定的实验测量出持液量这一重要参数。但很多情况下是利用有效相界面积和填料内平均液膜厚度进行相应估算得到的。

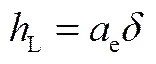
多为利用Nusselt液膜理论[11]得到的近似液膜厚度。

（21）

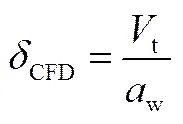
式中，p为规整填料比表面积；t为计算域内液相体积；w为液相在填料片上的润湿面积；L为液相在规整填料内按平均液膜厚度的合理性的有效流动角度，用式（18）进行求解得到。

为了评估用式（22）求解规整填料平均液膜厚度的合理性，在不同表面张力下，用CFD数值模拟得到的平均液膜厚度与用Nusselt液膜理论得到的平均液膜厚度进行比较，如图11所示，该数值模拟结果与Haroun等[26]的模拟结果相似。

从图11中可以看到，表面张力较低时，数值模拟计算得到的液膜厚度与Nusselt液膜理论得出的液膜厚度值几乎完全重合，这也说明数值模拟方法的可行性和准确性；随表面张力的增加，CFD/Nussel比值也逐渐增加，这说明液体在规整填料内的平均液膜厚度随着表面张力的增加而增加。这主要与液相在规整填料内的分布有关，而液相分布又是表面张力的函数。表面张力较低时，液相在规整填料片上分布较均匀，填料内平均液膜厚度较小；表面张力较高时，液相在规整填料内主要以沟流形式进行流动，平均液膜厚度较高。数值模拟的结果表明，只有液体在规整填料内均匀分布时，利用Nusselt液膜理论求解的平均液膜厚度才比较准确，式（21）适用于求解一维平均液膜厚度，液体在规整填料内以沟流形式进行三维流动时，利用Nusselt液膜理论求解的平均液膜厚度偏小。无论液相在规整填料内以怎么样的形式进行流动，利用CFD数值模拟的方法都可以准确地得到规整填料内的平均液膜厚度的大小。

5 结 论

本文采用计算流体力学中VOF的方法对液相在规整填料表面上的分布进行了三维数值模拟。该方法使液相在规整填料表面的分布可视化，数值模拟结果与已有文献中的经验公式进行了对比，同时给出了液相表面张力和黏度对规整填料的有效相界面积比和液膜厚度影响程度。

对于规整填料的最简化模型倾斜波纹板，数值模拟结果表明，液相在倾斜波纹板上的润湿面积随表面张力的减小而增加；随黏度的增加，润湿面积和液膜厚度都有微量的增加，并提出一个预测板上润湿面积的新模型。对规整填料结构单元的数值模拟表明，来自不同流道的液相流股在填料节点处发生混合和再分配现象，规整填料有效相界面积受表面张力对液相分布的影响而随表面张力的增加而减小；在填料节点处，液膜厚度达到最大值，规整填料各处的液膜厚度值均不相同，无法用Nusselt液膜理论进行准确估算。CFD数值模拟使液相在规整填料内的分布可视化，从而可以看到，液相在规整填料内的流动更倾向于向左右两边流动而不是沿着注射点垂直向下流动。

为了更好地理解规整填料塔内的基本流程和提高预测模型的准确性，还需要进行更多的研究。作者课题组将进一步利用CFD数值模拟考察规整填料的宏观结构和微观结构对液相分布和传质的影响。

符 号 说 明

a——波纹板上波纹的波峰，mm ae/ap——有效相界面积比 at——总面积，m2 aw——润湿面积，m2 B——规整填料片上峰宽，mm F——体积力源项，m/s2 g——重力加速度，m/s2 h——规整填料片上峰高，mm n，t——单位法向量和切向量 p——压力，Pa Re——雷诺数 S——动量源项 u——流体速度，m/s Vt——计算域内液相体积，m3 We——韦伯数 X，Y，Z——坐标，mm α——体积分数 αL——液相在规整填料内的有效流动角度 β——波纹板的倾角/规整填料波纹倾角，(°) θ——固液间接触角，(°) κ——自由表面曲率 λ——波纹板上波纹的波长，mm μ——物系黏度，Pa∙s ρ——流体密度，kg/m3 ——Nusselt液膜厚度，mm ——数值模拟得到的平均液膜厚度，mm σ——表面张力，N/m ω——润湿面积比率

[1] Mohamed Ali A，Janses P，Olujic Z. Experimental characterization and CFD simulation of gas distribution performance of liquid redistributors and collectors in packed columns[J].，2003，81：108-115.

[2] Alekseenko S V，Markovich D M，Evseev A R，et al. Experimental investigation of liquid distribution over structured packing[J].，2008，54：1424-1430.

[3] Bravo J L，Rocha J A，Fair J R. Mass transfer in gauze packings[J].，1985，64：91-95.

[4] Bravo J L，Rocha J A，Fair J R. Pressure drop instructure packings[J].，1986，3：45-49.

[5] Rocha J A，Bravo J L，Fair J R. Distillation columns containing structured packings：A comprehensive model for their performance. 1.Hydraulic models[J].，1993，32：641-651.

[6] Rocha J A，Bravo J L，Fair J R. Distillation columns containing structured packings：A comprehensive model for their performance. 2. Mass transfer model[J].，1996，35：1660-1667.

[7] Olujic Z. Development of a complete simulation model for predicting the hydraulic and separation performance of distillation columns equipped with structured packings[J].，1997，11：31-46.

[8] Olujic Z，Kamerbeek A B，de Graauw J. A corrugation geometry based model for efficiency of structured distillation packing[J].，1999，38：683-685.

[9] 徐崇嗣，楼建中，姜庆泉. 金属板波填料液流分布的研究[J]. 化工学报，1986，37（4）：402-412.

[10] Dangizer R. Simulating the turbulent mixing process in a static mixing element[J].，1978，60：1-10.

[11] Nusselt W. Die oberflaechenkondensateion des wasserdampfes[J].，1916，60：569-575.

[12] Shetty S A，Cerro R L. Estimation of liquid distribution and mass transfer parameters for ordered packings[C]//Institution of Chemical Engineers Symposium Series，1997a，142：853-864.

[13] Shetty S，Cerro R L. Fundamental liquid flow correlations for the computaion of desigh parameters for ordered packings[J].，1997b，36：771-783.

[14] 谷芳. 规整填料局部流动与传质的计算流体力学研究[D]. 天津：天津大学，2004.

[15] 陈江波. 高压下规整填料塔的计算传递和传质性能[D]. 天津：天津大学，2006.

[16] Fernandes J，Lisboa P F，Simões P C，et al. Application of CFD in the study of supercritical fluid extraction with structured packing：Wetpressure drop calculations[J].，2009，50：61-68.

[17] Hosseini S H，Shojaee S，Ahmadi G，et al. Computational fluid dynamics studies of dry and wet pressure drops in structured packings[J].，2012，18：1465-1473.

[18] Adachi T. Velocity and temperature profiles extending over the liquid and gas phases of two-phase flow falling down vertical plates[J].，2013，51：827-832.

[19] Raynal L，Royon-Lebeaud A. A multi-scale approach for CFD calculations of gas-liquid flow within large size column equipped with structured packing[J].，2007，62：7196-7204.

[20] Sun B，He L，Liu B T，et al. A new multi-scale model based on CFD and macroscopic calculation for corrugated structured packing column[J].，2013，59：3119-3130.

[21] Szulczewska B，Zbicinski I，Gorak A. Liquid flow on structured packing：CFD simulation and experimental study[J].，2003，26：580-584.

[22] Cooke J J，Armstrong L M，Luo K H，et al. Adaptive mesh refinement of gas-liquid flow on an inclined plane[J].，2014，60：297-306.

[23] Iso Y，Chen X. Flow transition behavior of the wetting flow between the film flow and rivulet flow on an inclined wall[J].，2011，133：091101-091107.

[24] Iso Y，Huang J，Kato M，et al. Numerical and experimental study on liquid film flows on packing elements in absorbers for post-combustion CO2capture[J].，2013，37：860-868.

[25] Rafati S A，Hosseini S H，Shojaee S，et al. CFD studies of pressure drop and increasing capacity in Mellapak plus 752.Y structured packing[J].，2011，34：1402-1412.

[26] Haroun Y，Raynal L，Alix P. Prediction of effective area and liquid hold-up in structured packings by CFD[J].，2014，92：2247-2254.

[27] Hosseini S H，Shojaee S，Ahmadi G，et al. Prediction of the effective area in structured packings by computational fluid dynamics[J].，2011，50：10833-10842.

[28] Dai C N，Li Q S，Chen B H. Pressure drop and mass transfer study in structured catalytic packings[J].，2012，98：78-87.

[29] Dai C N，Li Q S，Chen B H，et al. Simulation of structured catalytic packings in a bubble-point reactor[J].，2013，100：373-383.

[30] Hirt C W，Nichols B D. Volume of fluid (VOF) method for the dynamics of free boundaries[J].， 1981，39：201-225.

[31] Brackbill J U，Kothe D B，Zemach C. A continuum method for modelling surface tension[J].，1992，100：335-354.

[32] Lan H，Friedrich M，Armaly B F，et al. Simulation and measurment of 3-D shear-driven thin liquid film flow in a duct[J].，2008，29：449-459.

[33] Elioni M A，Fair J R. Liquid flow over textured surfaces. 1. Contact angles[J].，1999，38：284-291.

[34] Billet R，Schultes M. Predicting mass transfer in packed columns[J].，1993，16：1-9.

[35] Olujic Z，Behrens M，Colli L，et al. Predicting the efficiency of corrugated sheet structured packings with large specific surface area[J].，2004，18：89-96.

[36] Onda K，Takeuchi H，Okumoto Y. Mass transfer coefficients between gas and liquid phases in packed columns[J].，1968（1）：56-62.

Computational fluid dynamics study of liquid distribution on structured packing surface

TAN Liyuan1，YUAN Xigang1，KALBASSI Mohammad Ali2

（1State Key Laboratory of Chemical Engineering，Tianjin University，Tianjin 300072，China；2Air Products Public Limited Company，Walton on Thames，UK）

A volume of fluid (VOF) model of the computational fluid dynamics (CFD) method was used to simulate the liquid distribution on the structured packing surface. 3D simulation visualized liquid distribution. The results were used to estimate liquid film thickness and effective interfacial area ratio on the structured packing surface quantitatively，and the results were validated with existing correlations in the literature. Different systems with different surface tension values were used in the simulation and the effect of both surface tension and viscosity of liquid phase on liquid distribution were examined. Based on the simulation a new equation to predict the effective interfacial area ratio was proposed. The simulation results showed that the CFD method can be used as an effective tool to provide information on the details of the gas and liquid flows in complex packing geometries.

computational fluid dynamics (CFD); visualization; liquid film thickness; effective interfacial area ratio; surface tension; viscosity

TQ 028

A

1000–6613（2015）09–3221–12

10.16085/j.issn.1000-6613.2015.09.003

2015-02-03；修改稿日期：2015-04-20。

谭丽媛（1989—），女，硕士研究生，从事化工分离的研究。联系人：袁希钢，教授，从事化工传质分离及化工系统工程研究。E-mail yuanxg@tju.edu.cn。