一种基于单向辅助面滑模控制的无人机姿态控制器设计与仿真

吕海龙

（南京航空航天大学自动化学院，南京210016）

一种基于单向辅助面滑模控制的无人机姿态控制器设计与仿真

吕海龙

（南京航空航天大学自动化学院，南京210016）

根据无人战斗机机动飞行的仿真控制品质要求，应用了一种基于幂次趋近律单向辅助面滑模控制方法，用于解决无人机机动飞行状态下的非线性控制问题；首先建立了无人机六自由度数学模型；然后构建了控制系统的总体结构，并根据幂次趋近律单向辅助面滑模控制方法，设计了系统内外回路的姿态控制器；最后进行了仿真验证。仿真结果表明所设计的控制器具有良好的控制效果，保证了无人机机动飞行过程中的安全性与稳定性，且相对于常规滑模控制方法，具有更好的抗抖振能力。

无人战斗机；飞行控制；滑膜控制；仿真

由于无人机在军事和科学研究等领域的广泛应用，无人机研究已成为了一个比较热门的问题［1］。为保证无人机能安全有效地完成任务，需要解决的基本问题是无人机的控制。然而，由于无人机是一个复杂的多输入多输出系统［2］，随着现代无人机性能要求的提高，一些传统的线性化控制方法已经不能满足要求。

解决非线性问题的方法有很多，其中滑模控制是一种比较有效的方法［3］。但是传统滑模控制器切换时存在严重的抖振现象，为抑制抖振，有学者提出了一种单向辅助面滑模控制方法［4］。为改善单向辅助面滑模控制收敛速度慢的缺点，有人提出了基于幂次趋近律的单向辅助面滑模控制［5］。目前该控制方法未应用于无人机的控制领域。

本文将幂次趋近律单向辅助面滑模控制用于无人机的控制。首先基于无人机六自由度数学模型及幂次趋近律单向辅助面滑模控制方法，设计了内外回路的姿态控制器；然后通过仿真验证，结果表明该控制器对无人机有较好的控制效果，抗抖振效果比传统滑模要好。

1 问题描述

1.1 无人机数学模型

为设计姿态控制器，给出了无人机六自由度数学模型

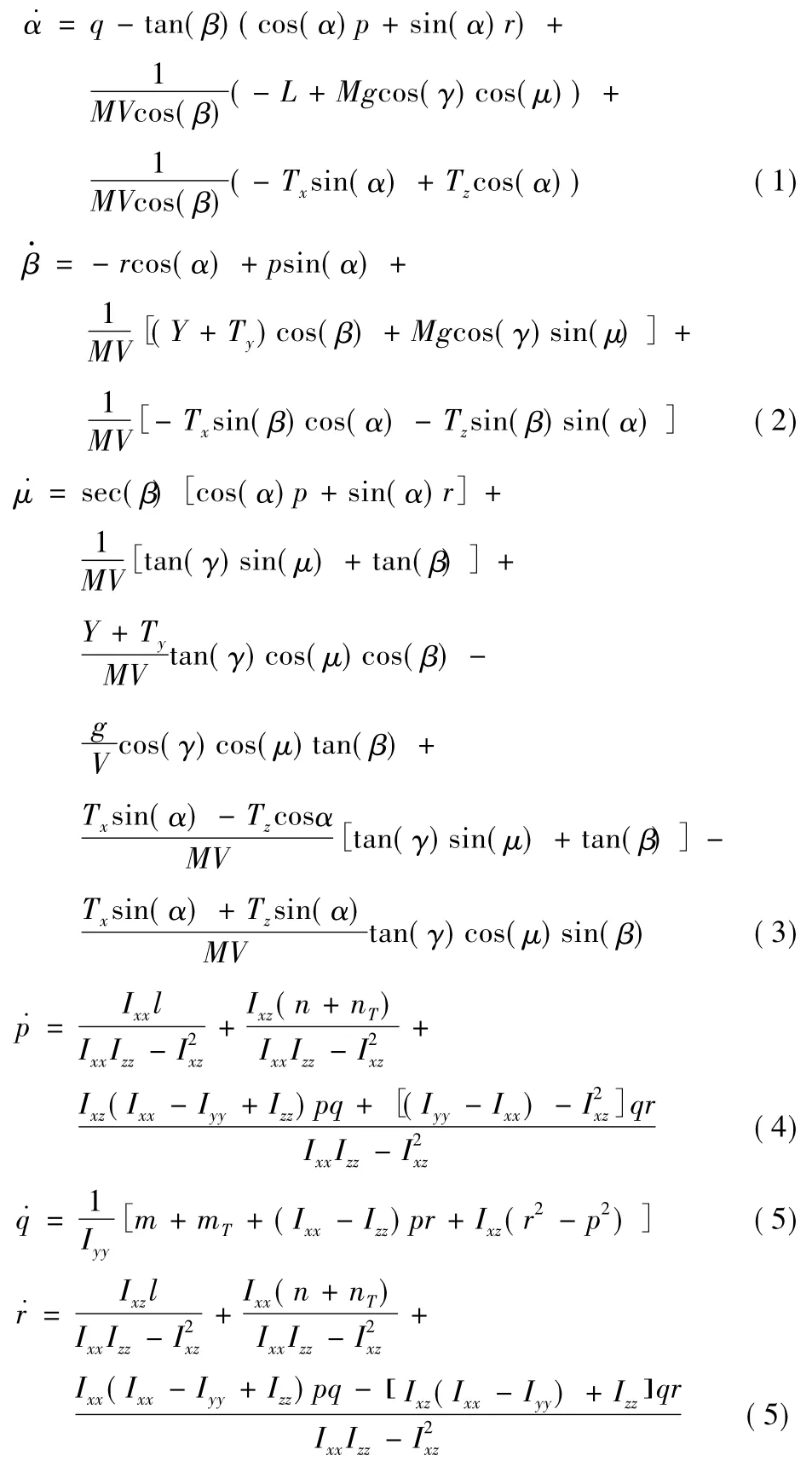
1.2 机动飞行性能指标

本文针对具有矢量推力的无人战斗机，研究其在机动飞行状态下的飞行性能与控制效果，最终控制目标：给出无人机动作指令，让无人机跟踪姿态指令信号。

依据飞行控制系统自动驾驶仪的基本性能指标要求，具体姿态角、马赫数、过载等参数给定信号的取值范围如下：

1）纵向姿态。常规情况下，俯仰角θ在15±°范围内，精度不低于0.5±°，而本例中为了验证无人机大机动的飞行情况，俯仰角将接近到90附近，此时已经到达常规控制律和一般最优控制律性能发生质变的边界点。

2）横侧向姿态。按照飞行控制系统原理，航向选择范围是360°。在改变航向的过程中建立滚转角，转弯角速度在飞行包线范围内以防止失速，滚转角φ在90±°范围内，精度不低于1±°。一般采用协调转弯，当稳态滚转角在60°左右时，侧滑角误差范围应小于2°，航向角ψ的精度不低于0.5±°。

3）高度与马赫数。随着高度的增加，飞机的各气动导数均呈非线性变化的趋势。此时要求高度控制精度误差在0.1%以内，马赫数保持控制器的精度为高于0.05。

2 控制器设计

2.1 控制原理

无人机运动方程的状态量x=［p，q，r；α，β，μ；V，γ，χ；x，y，z］T共有12个状态量，可以通过时标分离法把这些状态量分成如图1所示的4个回路，然后运用幂次趋近律单向辅助面滑模控制方法设计控制器。

x1=［p，q，r］T为角速率回路状态量，由于角速率状态变量变化较快，所以由其构成的回路也称为快变量回路，状态变量称为快变量。

x2=［α，β，μ］T为姿态回路状态量，由于这些状态变量变化的较慢，所以由其构成的回路也称为较慢变量回路，状态变量称为较慢变量。

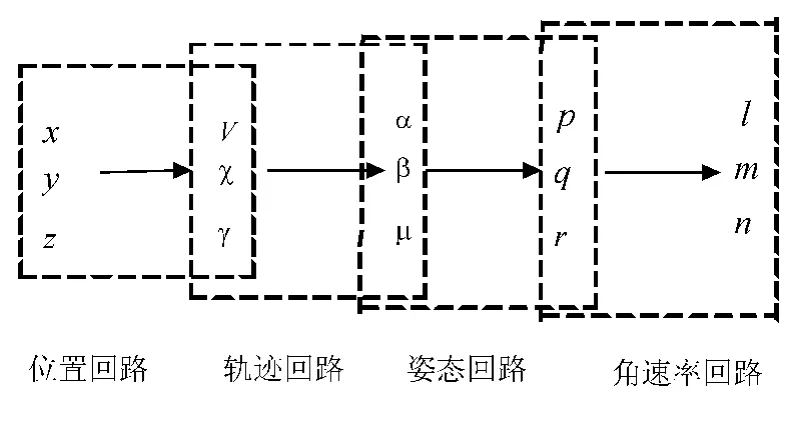
图1 控制原理图

x3=［V，γ，χ］T为轨迹回路状态量，由于该变量变化的慢，所以该回路也称为慢变量回路，状态变量称为慢变量。由于该状态量的产生是由推力和相对于速度轴的姿态矢量产生的法向力和侧向力经一次积分后形成的，所以它比姿态矢量更慢。

x4=［x，y，z］T为无人机对地位置矢量，位置回路状态量。

2.2 控制器设计

根据幂次趋近律单向辅助面滑模控制器的设计方法，首先选择切换面。

2.2.1 选择切换面

定义：

｛（x1，∫xi）|S1i（xi，∫xi）＜0；S2i（xi，∫xi）＜0；xi∈R；∫xi∈R｝为第0i个空间，同理可以定义空间1i，…，3i。如图2所示，i=1，…，n（n为系统维数）。

图2 切换面示意图

图3中，S1i，S2i为切换面。表达式为

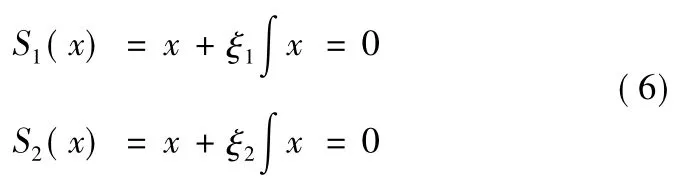
其中：ξ1=diag｛ξ11，…，ξ1n｝；ξ2=diag｛ξ21，…，ξ2n｝；S1（x）=［S11，…，S1n］T；S2（x）=［S21，…，S2n］T，的简写；ξ1i＞0；ξ2i＞0；ξ1i≠ξ2i。

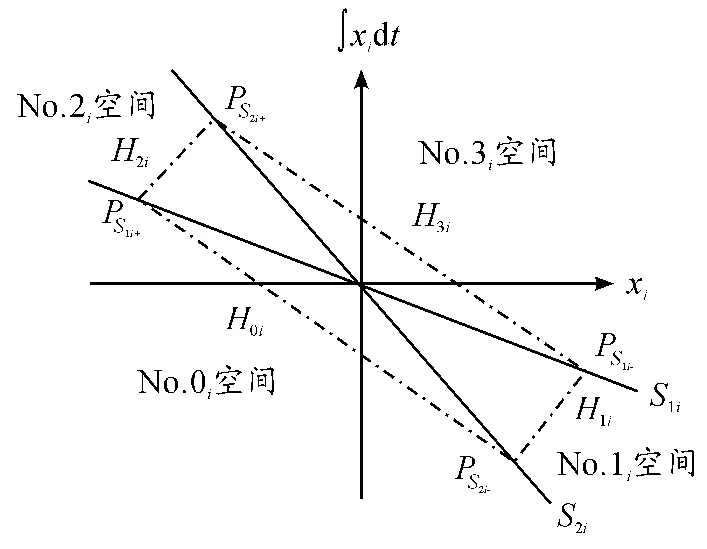
图3 单向辅助面示意图

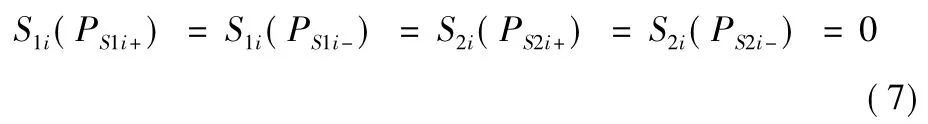
点PS1i+，PS1i-，PS2i+，PS2i-组成凸四边形，线段PS1i+PS2i-，PS1i-PS2i-，PS1i+PS2i+，PS1i-PS2i+构成单向辅助面H0i，H1i，H2i，H3i，单向辅助面方程如式（8）所示：

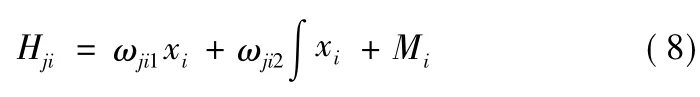
式（8）中：j∈｛0，1，2，3｝；ωji1≠0；Mi＞0，Mi是常数。

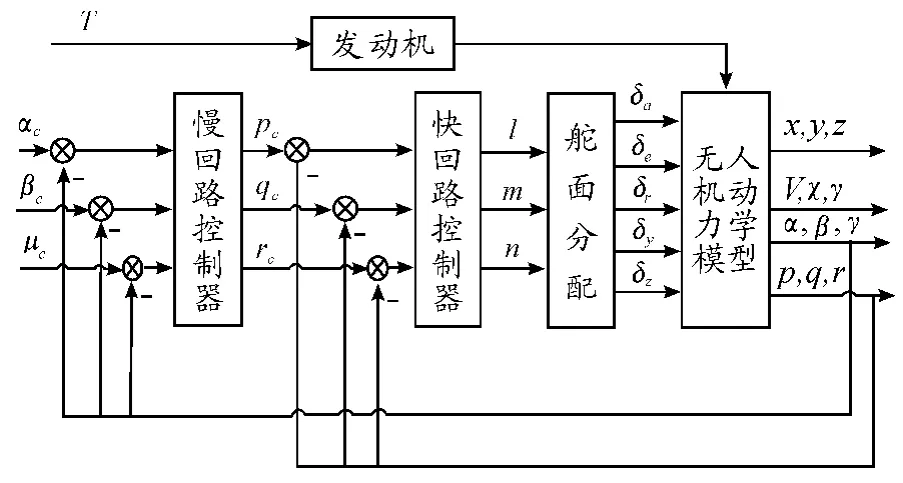
图4 飞行控制律结构

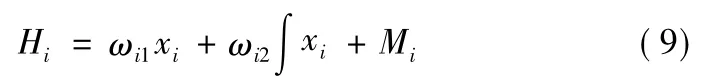
式（9）中，ωi1、ωi2为

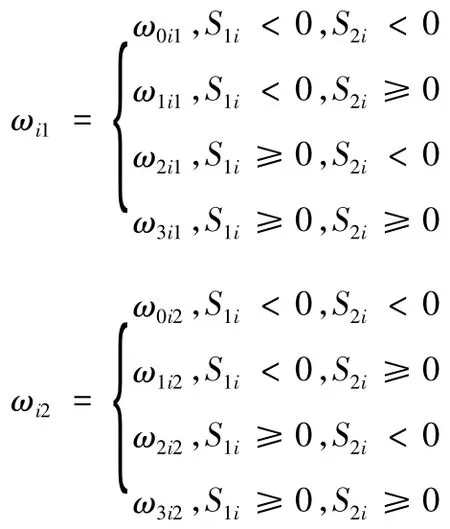
当前辅助面可记为

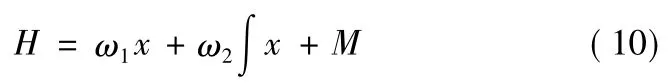
式（10）中：H=［H1，…，Hn］T；ω1=diag｛ω11，…，ωn1｝；ω2= diag｛ω12，…，ωn2｝；M=［M1，…，Mn］T。

2.2.2 控制器设计

针对快回路运动系统的3个通道，p，q，r分开设计控制律。首先对俯仰角速度p设计控制器如下：

1）选择切换面：

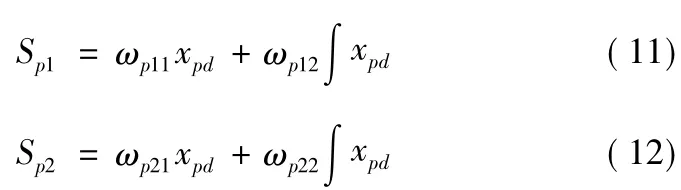
其中xpd-p误差指令：

其中，pc为指令信号，p为实际信号。选取ωp11=1，ωp12=2，ωp21=1，ωp22=1。

切换面Sp1，Sp2将空间分为4个子空间，0空间为同时满足Sp1＜0，Sp2＜0的子空间。1空间为同时满足Sp1＜0，Sp2≥0的子空间，2空间为同时满足Sp1≥0，Sp2＜0的子空间，3空间为同时满足Sp1≥0，Sp2≥0的子空间。

2）设计单向辅助面。在切换面Sp1上选取点PS11-（2，-1），PS11+（-2，1），在切换面Sp2上选取点。

在0空间内，点PS11+（-2，1），所在的面定义为单向辅助面Hp0，在1空间内点PS11-（2，-1），所在的面定义为单向辅助面Hp1，在2空间内点，PS11-（2，-1）所在的面定义为单向辅助面Hp2，在3空间内点PS11-（2，-1），所在的面定义为单向辅助面Hp3。

由此可得，单向辅助面方程为

3）设计控制器。根据幂次趋近律单向辅助面滑模控制器u表达式如下：

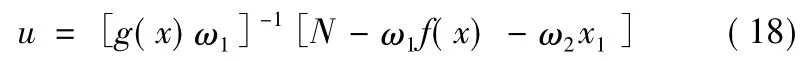
其中：N=λ（M-H）α，u=［δaδeδrδyδz］T，，，ω1=［ωp1ωq1ωr1］T，ω2=［ωp2ωq2ωr2］T，，λ＞0是可调参数。

同理可得到q、r、α、β、μ的单向辅助面分别为Hq、Hr、Hα、Hβ、Hμ，然后可分别求得控制器。

3 仿真结果及分析

仿真时根据1.1节无人机六自由度非线性微分方程采用文献［7］参数设计了数值仿真环境。对无人机眼镜蛇机动动作进行了仿真验证并将传统滑模设计的控制器与幂次趋近律单向辅助面滑模控制器进行对比，以验证幂次趋近律单向辅助面滑模算法具的控制效果。

仿真的初始配平条件为：高度2 000 m，马赫数0.35，油门开度85%，无人机处于定直平飞状态。通过传统滑模控制器和基于幂次趋近律的单向辅助面滑模控制器仿真图（图5～图15）。

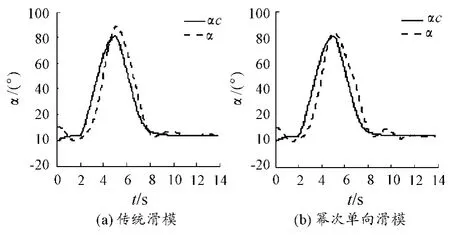
图5 迎角仿真图

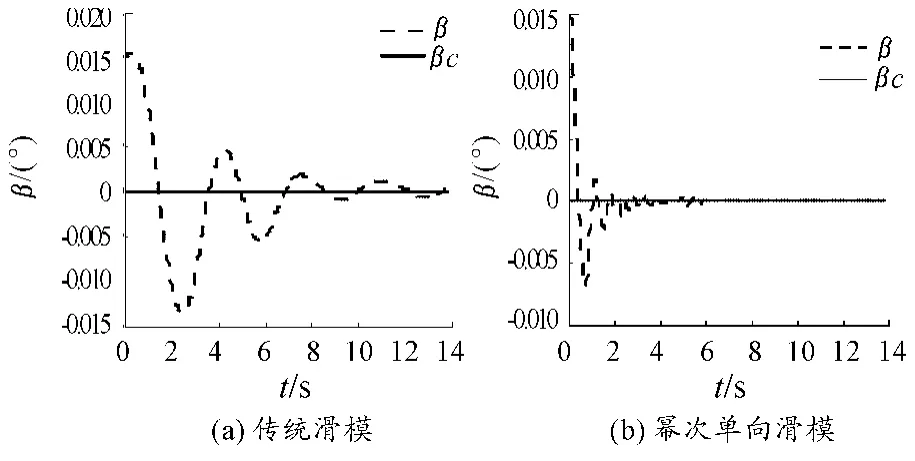
图6 侧滑角仿真图

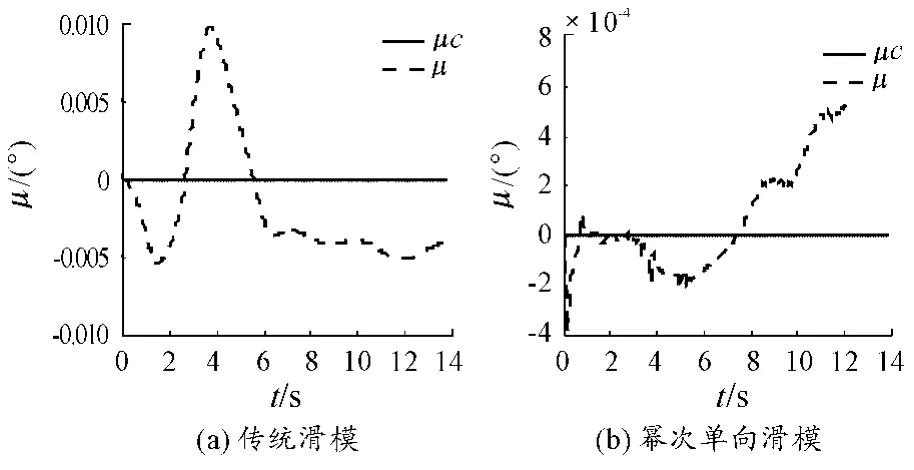
图7 滚转角仿真图

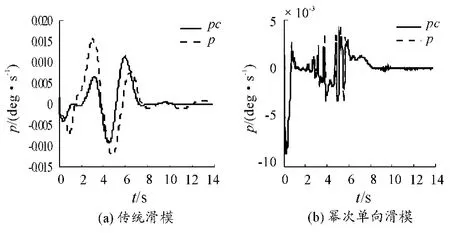
图8 滚转角速度仿真图

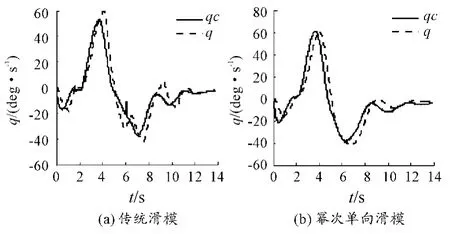
图9 俯仰角速度仿真图

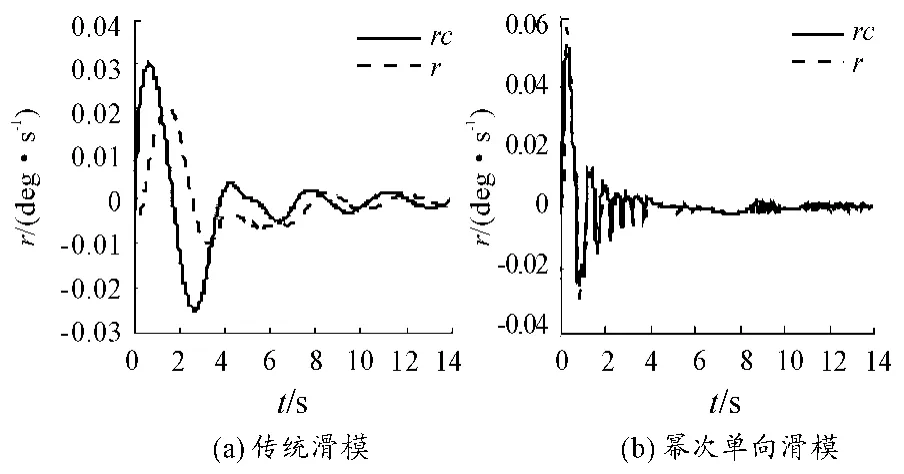
图10 偏航角速度仿真图

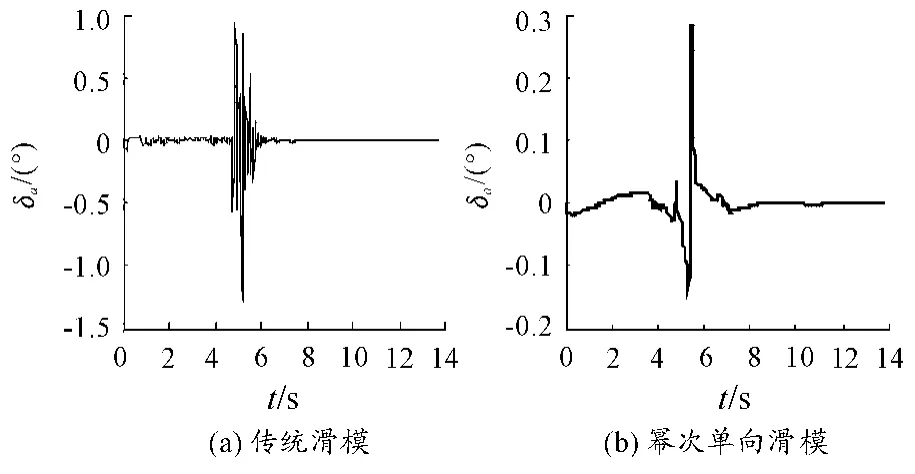
图11 副翼偏角仿真图

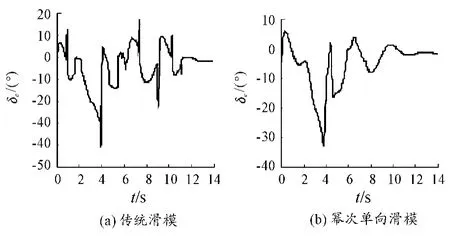
图12 升降舵偏角仿真图

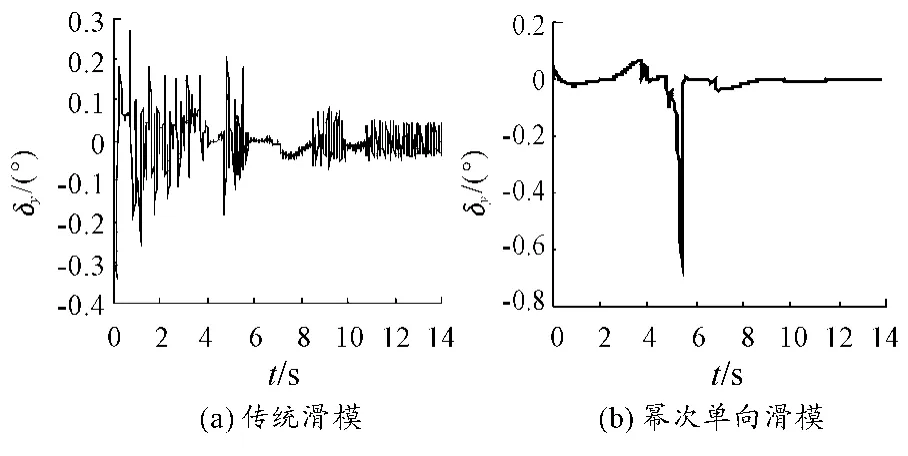
图13 方向舵偏角仿真图

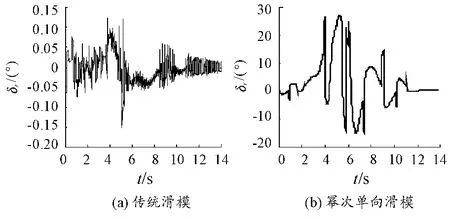
图14 推力矢量侧向偏角仿真图

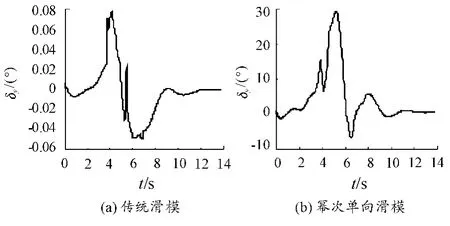
图15 推力矢量纵向偏角仿真图

仿真结果分析：

由图5～图10，姿态角和姿态角速度跟踪仿真曲线可知，两种控制器都可以较准确、快速的跟踪参考指令信号，由图5迎角仿真曲线，可知，基于幂次趋近律的单向辅助面滑模能够更准确、快速的跟踪上参考迎角指令。由图6，侧滑角仿真跟踪曲线，可知，传统滑模控制器侧滑角曲线图7（a），抖振比较明显，收敛速度较慢，而基于幂次趋近律的单向辅助面滑模控制的侧滑角曲线图7（b），在0～2 s内抖振较明显，2～4 s略微有抖振，4 s以后能较快速的收敛。体现出基于幂次趋近律的单向辅助面滑模控制器良好的抗抖振性及快速收敛性。

图8、图9、图10分别为传统滑模和基于幂次趋近律的单向辅助面滑模控制器滚转角速度p、俯仰角速度q、偏航角速度r仿真曲线，可知p、q、r均在迎角达到极大值时而达到极大值。之后，随着迎角的减小而不断减小。由此可知两种控制算法下的仿真模型是正确的。由上述角速率仿真图比较可知，基于幂次趋近律的单向辅助面滑模控制器跟踪控制效果较好。

图11、图12、图13、图14、图15分别为副翼偏角、升降舵偏角、方向舵偏角、推力矢量侧向偏角、推力矢量纵向偏角，表明两种控制方法的控制舵面均在合理偏转范围。由于眼镜蛇机动为大迎角飞行机动，通过控制舵面响应曲线可知，基于控制力矩的分配，随着角度的增加，需要气动舵面和推力矢量共同控制歼击机超机动动作。其中，由图12可知基于幂次趋近律的单向辅助面滑模控制下的升降舵曲线变化更平稳，抖振较小，而传统滑模控制器的升降舵偏角曲线有明显的抖振，由此亦可以证明幂次趋近律的单向辅助面滑模控制器抗抖振效果要优于传统滑模。

4 结束语

本文引入了基于幂次趋近律单向辅助面滑模控制算法用于无人战斗机非线性控制，根据响应时间将无人战斗机的控制回路分为快回路和慢回路，分别由幂次趋近律单向辅助面滑模控制方法设计了控制器，通过仿真验证发现，该方法用于无人战斗机控制有较好效果。虽然幂次趋近律单向辅助面滑模控制对抖振的抑制较传统滑模要好，但也有一定的抖振，在实际的工程应用中需要进一步考虑系统抖振的抑制。

［1］龙威林.无人机的发展与应用［J］.产业与科技论坛，2014（8）:15-21.

［2］席庆彪，袁冬莉，闫建国.无人机横侧向飞行控制系统研究［J］.飞行力学，2004（4）:71-75.

［3］郭艳艳，陈澜，杨常伟.无人机着陆抗风鲁棒H∞控制器设计研究［J］.计算机测量与控制，2010（2）:67-72.

［4］陶洪峰，胡寿松.具有饱和死区非线性输入的自适应滑模跟踪控制［J］.信息与控制，2009，38（3）:112-116.

［5］于媛媛，吴庆宪，姜长生.基于幂次趋近律的单向辅助面滑模控制［J］.电光与控制，2014（4）:49-54.

［6］鲁可.无人战斗机着舰飞行控制研究［D］.南京:南京航空航天大学，2013.

［7］任泽玉.先进歼击机超机动飞行运动建模与控制研究［D］.南京:南京航空航天大学，2013.

［8］Utkin VI.Sliding mode control design principles and applications to electric drives.IEEE Transactions on Industrial Electronics，1993

［9］张聪，田福礼，刘超，等.超机动飞机飞行控制及大迎角飞行品质研究［J］.航空工程进展，2011（4）:127-132.

［10］文传源.现代飞行控制［M］北京:北京航空航天大学出版社，2004:243-247.

［11］张明廉.飞行控制系统［M］.北京:航空工业出版社，1994.

［12］陈哨东，孙隆和.先进无人战斗机（UCAV）系统概念［J］，火力与指挥控制，2003（6）:74-79.

［13］Slotine J J，Sastry S S.Tracking control of nonlinear systems using sliding surfaces with application to robot manipulators［J］.International Journal of Control，1983.

（责任编辑杨继森）

Based on Sliding Mode Control with Unidirectional Auxiliary Surfaces of UAV Attitude Controller Design and Simulation

LYU Hai-long
（College of Automation Engineering，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，China）

According to the requirements of UCAV flight control quality，the application of a kind of unidirectional auxiliary plane sliding mode control based on the exponential reaching law method was used to solve nonlinear control under the state of UCAV maneuvering flight problems.UCAV was established by the six degrees of freedom mathematical model.Then the general structure of the control system was constructed，and according to the exponential reaching law one-way auxiliary plane sliding mode control method，we designed the system inside and outside loop attitude controller.Finally the simulation was verified. The simulation results show that the designed controller has good control effect，which ensures the security and stability in the process of UAV maneuvering flight，and has better ability to resist chattering compared to the conventional sliding mode control method.

UCAV；flight control；sliding mode control；simulation

吕海龙.一种基于单向辅助面滑模控制的无人机姿态控制器设计与仿真［J］.四川兵工学报，2015（11）：112-117.

format：LYU Hai-long.Based on Sliding Mode Control with Unidirectional Auxiliary Surfaces of UAV Attitude Controller Design and Simulation［J］.Journal of Sichuan Ordnance，2015（11）：112-117.

V249

A

1006-0707（2015）11-0112-06

10.11809/scbgxb2015.11.030

2015-04-15

吕海龙（1983—），男，硕士研究生，主要从事无人机飞行控制研究。