装甲目标毁伤概率计算方法

李建平，熊伟，程军，丛日圆

（63863部队，吉林白城137001）

装甲目标毁伤概率计算方法

李建平，熊伟，程军，丛日圆

（63863部队，吉林白城137001）

为了研究装甲目标毁伤概率计算方法，把装甲目标各部位按功能进行了区域划分和毁伤概率分析，以各区域的毁伤概率和命中概率为自变量给出了整体毁伤概率的计算公式。在各区域正面投影的基础上结合命中概率的数学定义，用蒙特卡洛随机投点方法进行仿真计算，并给出了算例。算例结果的数据拟合和相关性分析表明，该计算方法合理可行。

装甲目标；毁伤；蒙特卡洛；毁伤概率；相关性分析

装甲目标是指直接用于战斗或装有专有设备和装置，用来保障装甲机械化部队执行任务或完成其他作战保障任务的装甲车辆，一般分为装甲战斗车辆和装甲保障车辆［1］。典型的装甲车辆有：坦克、装甲运兵车等。针对装甲目标的特性，人们研发了反装甲弹药，常用的有穿甲弹、破甲弹和碎甲弹等。

毁伤作用是指对目标摧毁、杀伤以便造成减弱或丧失其战斗力的作用。毁伤能力是以一定的指标表达毁伤的作用，是对弹药毁伤作用的量化理解［2］。对于确定的弹目系统，毁伤能力可以理解为目标的毁伤概率。装甲目标因其自身的特点在战争中扮演了重要的角色，同时也成为敌我双方重点打击的目标，对其毁伤概率计算方法进行研究具有重要意义。

1 毁伤概率计算

装甲目标的毁伤是由部件或系统的毁伤导致的，部件或系统的毁伤程度决定了整个目标的毁伤级别，而部件或系统的毁伤与作用其上的毁伤元及参量有关［3］。

1.1 部件毁伤概率分析

为了确定装甲目标各部件的毁伤概率，将装甲目标分解为传动装置、弹药舱、发动机舱、成员舱、炮塔等部件。因毁伤元的多样性，以金属射流对坦克的毁伤为例进行分析。

1）传动装置：金属射流对其毁伤概率如图1［4］所示；

2）弹药舱：金属射流直接命中，造成100%的毁伤；

3）发动机舱：金属射流直接命中，造成100%的毁伤；

4）炮塔：金属射流直接命中，造成100%的毁伤；

5）成员舱：金属射流击穿成员舱，造成的毁伤与穿孔直径有关，如图2［4］所示。

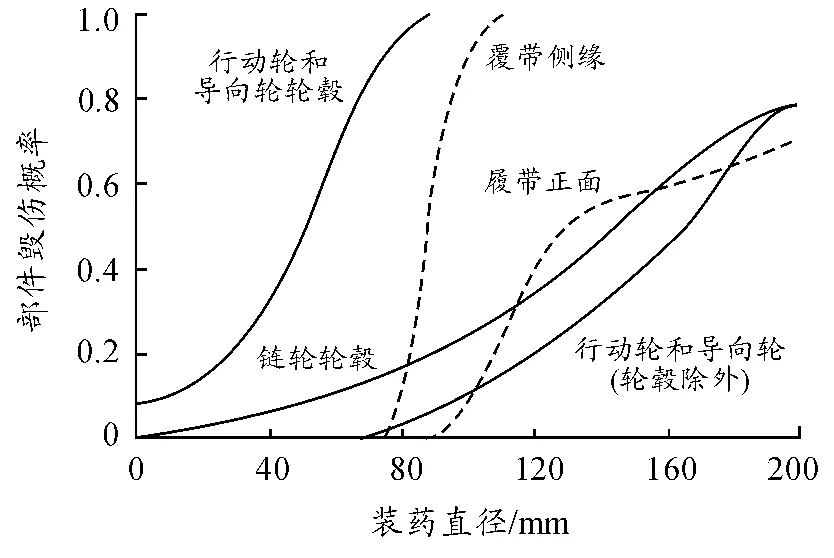
图1 射流对传动部件毁伤概率曲线

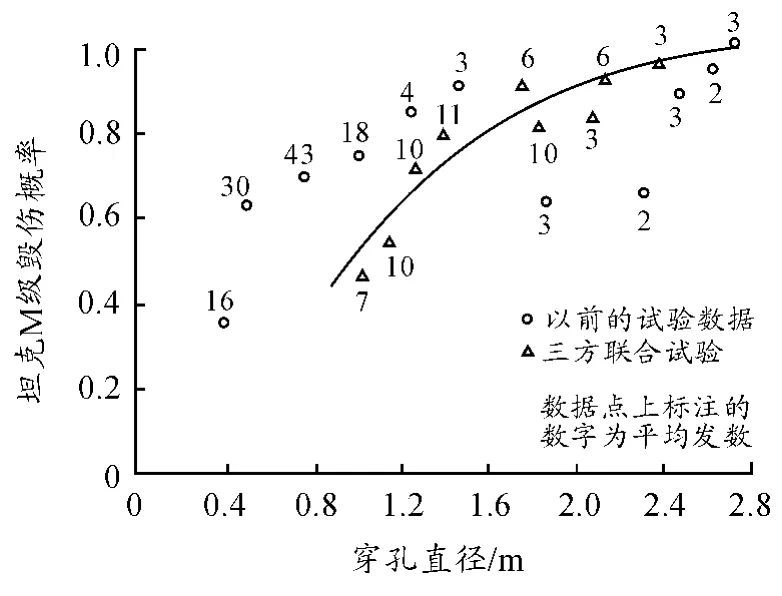
图2 乘员舱毁伤概率曲线

假设射流从正面命中坦克，将坦克从正面投影，得到坦克可能被毁伤的部件投影图，如图3、图4所示。

图3 坦克功能区划分

图4中1区为炮塔，2区为成员舱，3区为弹药舱，4、5区为传动装置。根据前文所述和图4、图5的曲线可知破甲弹（装药直径为120 mm，设穿孔直径为2 cm）对图4中各部件的毁伤概率如表1所示。

图4 坦克功能区正面投影

表1 不同区域毁伤概率

1.2 命中概率计算

命中概率是指给定的武器系统在同一条件下向同一目标发射N发弹丸，有n发命中目标，如图5所示，则其命中概率可以表示为［5］

在给定的目标区域D，命中概率的计算，可用下面公式［6］计算

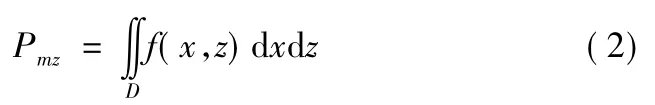
式中：Pmz为命中概率；f（x，z）为弹着点的概率密度函数。

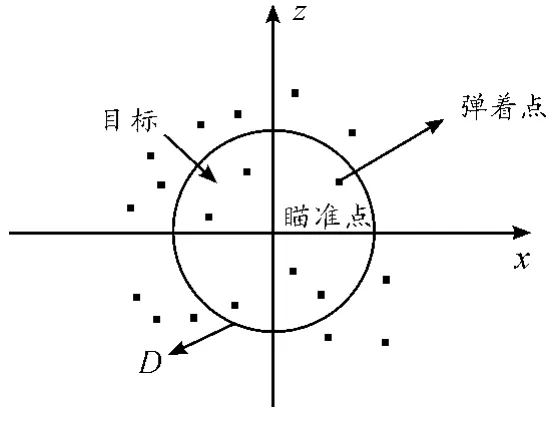
图5 平面目标坐标系

在图4基础上建立以O点为瞄准点的目标坐标系，如图6所示。以图6中区域①～⑤为式（2）的积分域，设弹着点坐标为xi、zi，均值和方差分别为：，利用式（2）便可计算出在一定射击条件下各个区域的命中概率。由于没有准确的f（x，z）表达式，常用蒙特卡洛随机投点法求解决此类积分［7］。

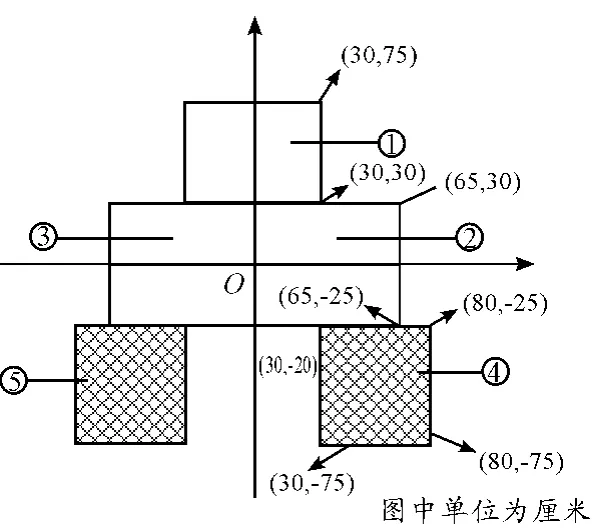
图6 坦克投影坐标系

设在一定弹目系统和射击条件下，装甲目标各功能区的命中概率为p1，p2，…，pn、毁伤概率为w1，w2，…，wn，则目标的毁伤概率

2 算例

以图6所示目标为例，用口径为120 mm的破甲弹分别在500 m、1 000 m、1 500 m、2 000 m处进行射击，计算弹丸对区域①～⑤的命中概率。弹药指标如表2所示。

在1 000 m处，分每组为1发、2发、3发、4发4种情况向目标射击，每种情况重复10次，求其平均值，用蒙特卡洛随机投点的方法进行模拟计算，计算结果如表3及图7所示。

在500 m、1 000 m、1 500 m、2 000 m处，每组为2发，向目标射击，每距离重复10次，计算其平均值，用蒙特卡洛随机投点的方法进行模拟计算，计算结果如表4及图8所示。

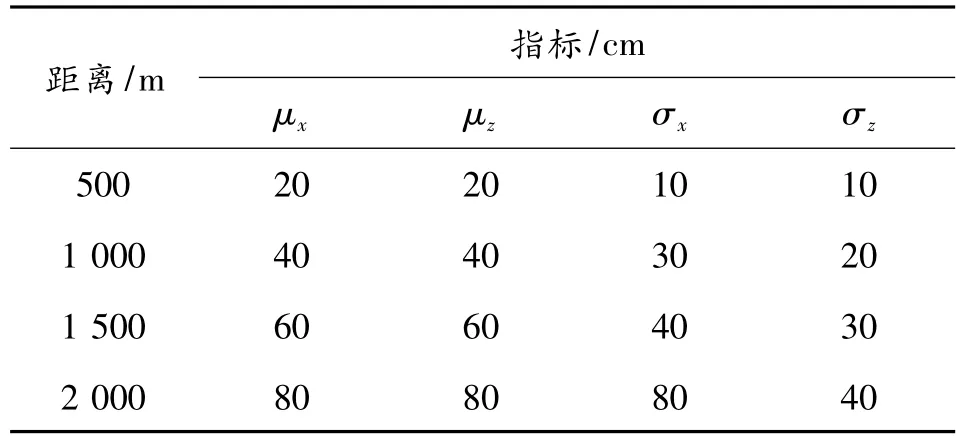
表2 120 mm破甲弹指标（假设）

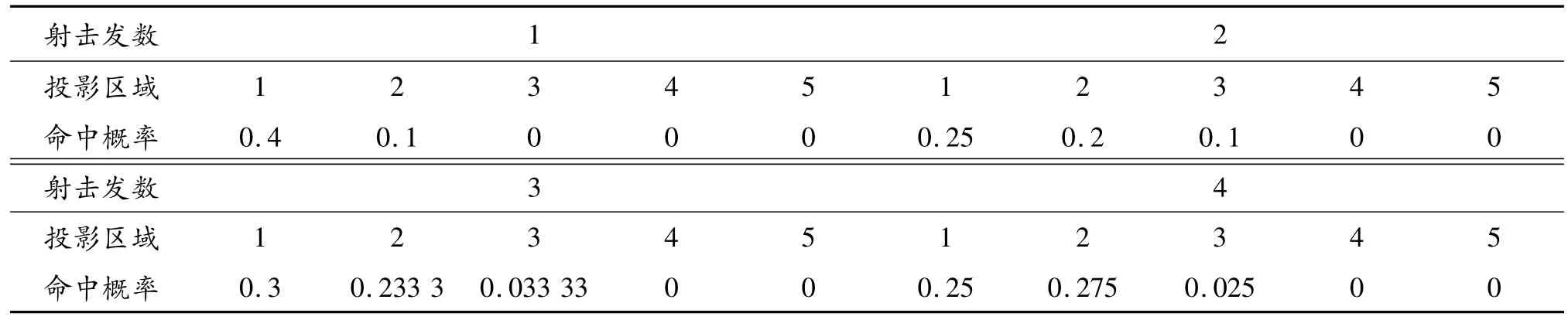
表3 1 000 mm处命中概率

图7 1 000 m处命中情况

表4 2发时不同距离命中概率

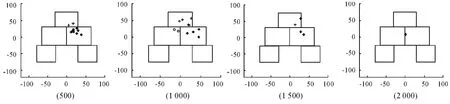
图8 不同距离处命中情况

把表1、表3、表4中的数据，代入式（3），计算120 mm破甲弹射对坦克的毁伤概率，计算结果如表5所示。

表5 坦克毁伤概率

以发数、距离和毁伤概率为横纵坐标，作毁伤概率散点图并进行数值拟合，散点图如图9、图10所示，拟合结果见式（4）与式（5）。

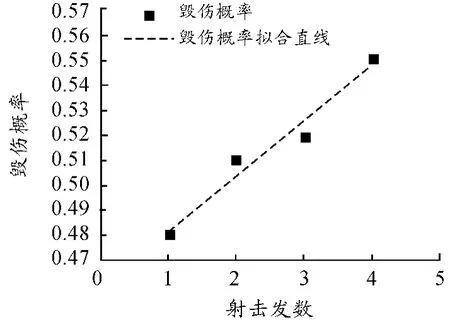
图9 射击发数与毁伤概率折线

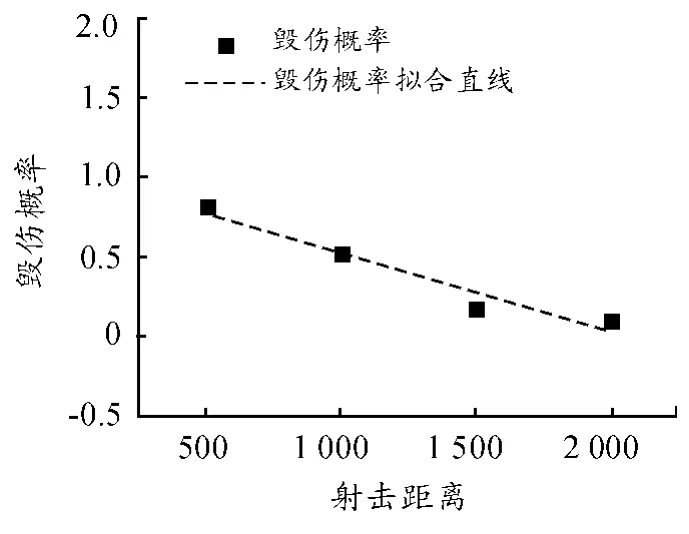
图10 射击距离与毁伤概率拟合曲线

由图9可知当射击距离为1 000 m时，随射击发数的增加坦克的平均毁伤概率呈上升趋势。对图9的数据点和拟合曲线进行皮尔逊相关性分析。相关性分析结果如表6所示。

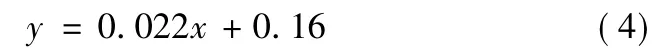
式中：y为毁伤概率、x为射击发数，拟合校正决定系数为0.952。

由图10当射击发数为2时，随射击距离的增加坦克的毁伤概率总体呈下降趋势。对图10的数据点和拟合曲线进行皮尔逊相关性分析。相关性分析结果如表7所示。y=-0.000 049 2x+1.015（5）式中：y为毁伤概率、x为射击距离，拟合校正决定系数为0.925。

表6 毁伤概率与射击发数相关性分析结果

表7 毁伤概率与射击发数相关性分析结果

3 结论

由前文计算结果可知：在特定弹目系统内，射击距离一定时，装甲目标的毁伤概率与射弹数呈正相关关系；射弹数一定时，装甲目标的毁伤概率与射击距离呈负相关关系，符合此类现象的客观统计规律。因此通过对装甲目标区域划分确定各区域毁伤概率、蒙特卡洛仿真法计算装甲目标不同区域的命中概率切实可行，该方法对工程实践有实际的指导意义。

［1］樊胜利，柏彦奇，李保国.装甲目标威胁评估智能计算方法研究［J］.装备指挥技术学院学报，2011，22（2）:45 -45.

［2］王凤英，刘天生.毁伤理论与技术［M］.北京:北京理工大学出版社，2009:194-194.

［3］李向东，杜中华.目标易损性［M］.北京:北京理工大学出版社，2013:119-119.

［4］王维和，李惠昌.终点弹道学原理［M］.北京:兵器工业出版社，2005.

［5］林海，高坤.基于加权蒙特卡洛法的新型攻坚弹射击命中概率［J］.四川兵工学报，2010，31（10）:119-119.

［6］潘承泮，韩之君，章渭基.武器弹药试验和检验的公算与统计［M］.北京:国防工业出版社，1980:79-79.

［7］王刚，段晓君，王正明.基于蒙特#卡罗积分法的面目标精度评定方法［J］.系统工程与电子技术，2009，31（7）: 1682-1682.

［8］房凌晖，郑翔玉，汪伦根，等.坦克装甲车辆主动防护系统发展研究［J］.装备环境工程，2014，11（1）:63-67.

（责任编辑周江川）

Armored targets Damage Probability Calculation Method

LI Jian-ping，XIONG Wei，CHENG Jun，CONG Ri-yuan
（The No.63863rdTroop of PLA，Baicheng 137001，China）

In order to study the damage probability calculation method armored targets，the armored target various parts of the region was divided by function and damage probability analysis，and the formula for calculating the probability of the overall damage was given by taking probability and hit probability to damage the regions as independent variables.Combined with the hit probability on the basis of the regional front projection on the mathematical definition，we had simulation calculation with Monte Carlo stochastic investment point method and gave examples.Numerical results of data fitting and correlation analysis show that the calculation method is reasonable and feasible.

armored targets；damage；Monte Carlo；damage probability；correlation analysis

李建平，熊伟，程军，等.装甲目标毁伤概率计算方法研究［J］.四川兵工学报，2015（11）：45-48.

format：LI Jian-ping，XIONG Wei，CHENG Jun，et al.Armored targets Damage Probability Calculation Method［J］.Journal of Sichuan Ordnance，2015（11）：45-48.

TJ811

A

1006-0707（2015）11-0045-04

10.11809/scbgxb2015.11.013

2015-06-15

李建平（1977—），男，硕士，工程师，主要从事武器弹药毁伤效能试验及评估研究。