直线运动和人类社会

杨斌

一、与人类生活有关的问题

近来，驾驶的安全问题一直是引起大众关注的焦点，利用物理学的知识可以来研究安全问题，并且尽可能的避免危险的发生.

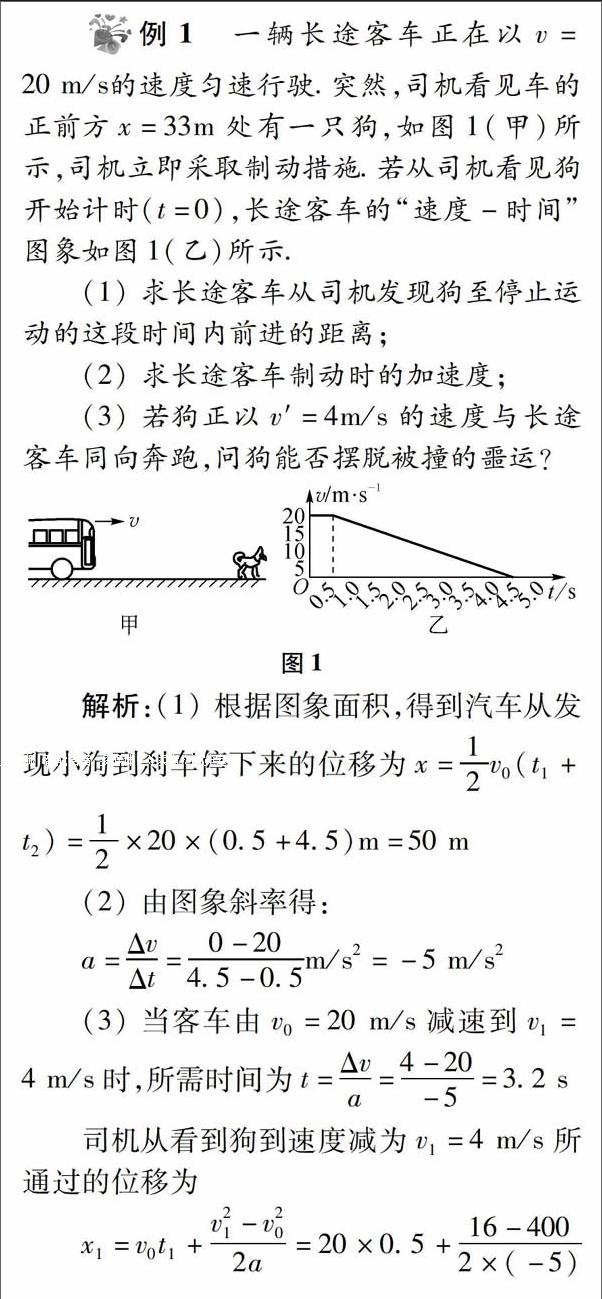
例1 一辆长途客车正在以v=20 m/s的速度匀速行驶.突然，司机看见车的正前方x=33m处有一只狗，如图1（甲）所示，司机立即采取制动措施.若从司机看见狗开始计时（t=O），长途客车的“速度一时间”图象如图1（乙）所示.

（1）求长途客车从司机发现狗至停止运动的这段时间内前进的距离：

（2）求长途客车制动时的加速度；

（3）若狗正以v'=4m/s的速度与长途客车同向奔跑，问狗能否摆脱被撞的噩运？

解析：（1）根据图象面积，得到汽车从发现小狗到刹车停下来的位移为

（2）由图象斜率得：

（3）当客车由

司机从看到狗到速度减为v₁=4m/s所通过的位移为

而狗通过的位移为x₂=（t₁+t）=4×（0.5+3.2）=14.8 m，x₂+33 =47.8 m

因为x₁>x₂+33，所以狗将被撞.

高速公路小车的限速达到120 km/h，也就是达到33.33m/s，将是上题中的1.67倍，那么他的刹车距离将会达到127.78m左右，所以高速公路上的安全距离规定为200 m，这是充分考虑到驾驶人员的反应时间和安全.

二、与人类运动有关的问题

利用物理学知识对人体的运动潜能进行合理的训练，结合生物方面的研究，这样可以提高人类的运动能力.

例2 原地起跳时，先屈腿下蹲，然后突然蹬地.从开始蹬地到离地是加速过程（视为匀加速）加速过程中重心上升的距离称为“加速距离”.离地后重心继续上升，在此过程中重心上升的最大距离称为“竖直高度”.现有下列数据：人原地上跳的“加速距离”d₁=0.50m，“竖直高度”h₁=1.0 m；跳蚤原地上跳的“加速距离”d₂=0.00080m，“竖直高度”h₂=0.10m.假想人具有与跳蚤相等的起跳加速度，而“加速距离”仍为0.50m，则人上跳的“竖直高度”将达到多少？

解析：用a表示跳蚤起跳的加速度，t表示离地时的速度，则对加速过程和离地后上井过程分别有v²=2ad²=2gh²