同轴结构半径突变处补偿电容的计算分析
焦重庆 李明洋
(新能源电力系统国家重点实验室(华北电力大学)北京 102206)
0 引言
在电力测试线、GIS 套管、微波传输和耦合电路等同轴结构中,常会出现导体半径的突变。半径的突变会激发起高阶电磁模式[1]。在单模工作状态下,这些高阶模式主要分布在突变处附近,沿两侧会呈指数衰减。文献[2-4]基于全波的方法分析得出,高频时,在半径突变处两边的外导体上电位连续、电流不连续。在某些实际情况中,比如GIS 的开关操作,同轴导体外径在半米以内,而最高感兴趣的频率一般不超过100MHz[5-7],此时波长远大于同轴结构的外径。半径突变对横向电磁场(Transverse Electric and Magnetic Field,TEM)模传播的影响可等效为一个位于半径突变处的集总补偿电容[4]。
文献[4]基于全波的方法,可以考虑补偿电容的频变效应,推导过程和计算公式均较复杂;对于本文尺寸,参照文献[4]的计算,静态补偿电容与100MHz 时的补偿电容的相对误差不超过5%,在工程应用允许的误差范围内,即可以忽略补偿电容的频变效应,用静态电容代替。本文利用分离变量法,基于同轴结构半径突变处电位分布的精确计算,推导了静态补偿电容的精确计算模型。该计算模型计算简单,便于工程应用。
1 计算模型
同轴结构的半径突变模型如图1 所示。半径突变处位于区域A、B 的分界面oo'上,假设突变处两边的同轴线均匀且无限延伸。取同轴线的轴向为z向,z 轴的坐标原点在半径突变处的分界面上,z 轴的正方向由区域A 指向区域B。内导体的半径为r1,区域A 外导体的内半径为r2,区域B 外导体的内半径为r3。内导体施加电压U0,外导体电位为0。
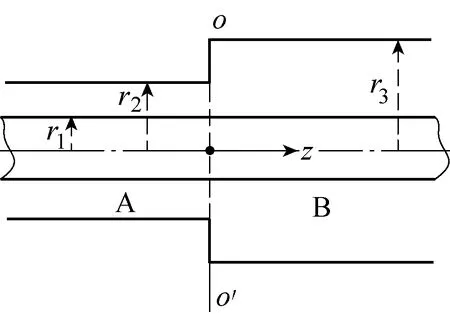
图1 同轴结构半径突变模型Fig.1 Model of abrupt change of radius in coaxial structure
图1 所示结构的电路模型可由特征阻抗分别为Z0A、Z0B,传播常数分别为γ0A、γ0B的传输线和表征半径突变效应的补偿电容Cc来等效,如图2 所示。
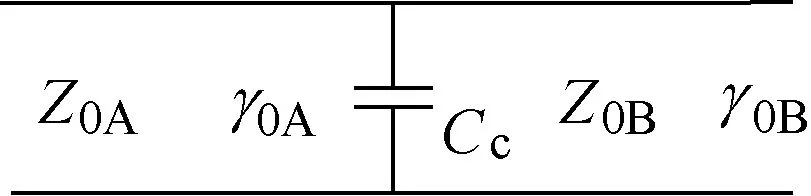
图2 半径突变的同轴结构的等效电路Fig.2 Equivalent circuit of a coaxial structure with abrupt change of radius
先利用分离变量法[8]解出区域A、B 的电位分布,再由导体上的电荷分布及内外导体间的电压求出补偿电容Cc的值。
区域A 的电位分布表达式为
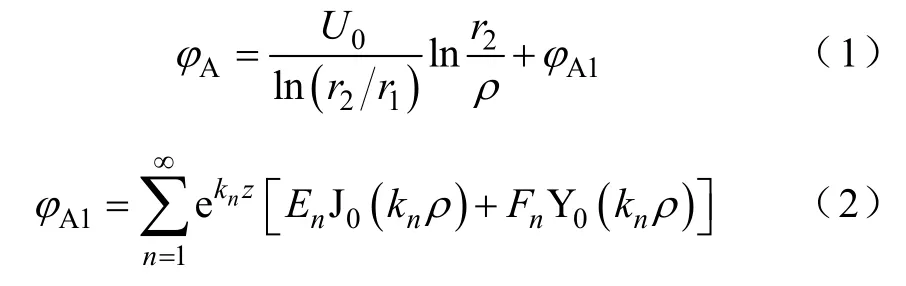
式中,J0、Y0分别为第一、第二类贝塞尔函数;U0为内外导体间的电压(V);式(1)等号右边的第一项表示均匀同轴线内的电位分布。φA1是利用分离变量法解得的圆柱坐标系中拉普拉斯方程的一般解[9],φA1表示由于半径突变的存在引起的电位分布的畸变,并且 φA1在区域A 中的内外导体表面边界上满足条件
将式(3)、式(4)分别代入式(2),可得
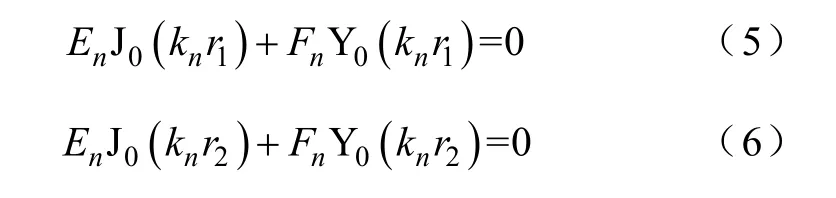
求解由式(5)、式(6)组成的方程组,若En、Fn有非0 解,必有系数行列式为0,如式(7)所示。
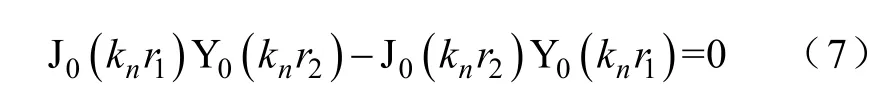
求解式(7),得kn为一系列正数[10]。
由式(5)可得

将式(8)代入式(2),并定义
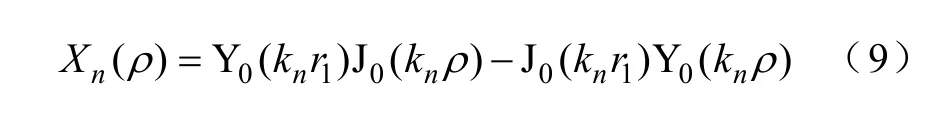
则式(2)可表示为

式(10)、式(15)中的未知系数An、Bm可利用区域A、B 分界面上的边界条件[11]确定,边界条件为

由式(12)、式(13)可以证明,当n ≠i 时,式(22)中等号左边的项的积分为0,则式(22)可以简化为
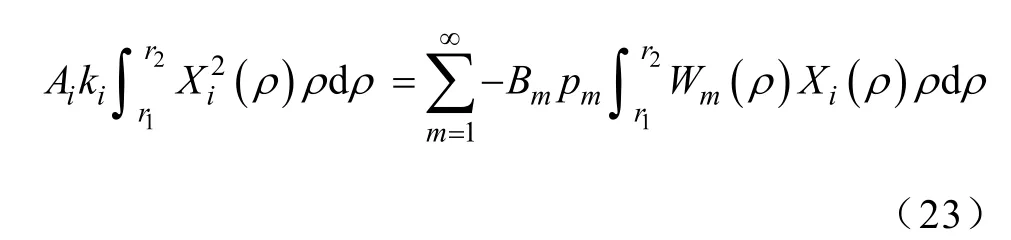
式(23)表明系数iA 可以用系数Bm表示,即

在z=0,r1< ρ<r3边界上,由式(19)、式(20)可得

将式(1)、式(14)代入式(26),并利用正交性得
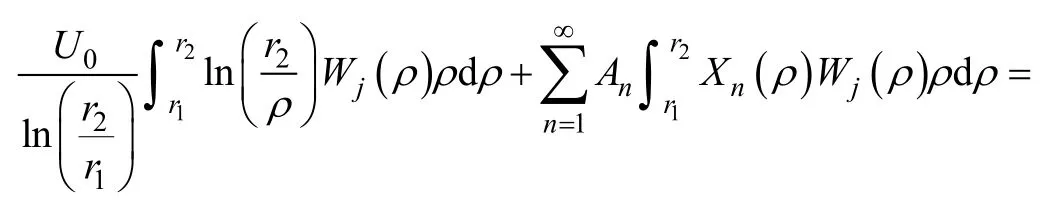

将式(24)代入式(27),整理式(27)可得关于Bm的线性方程
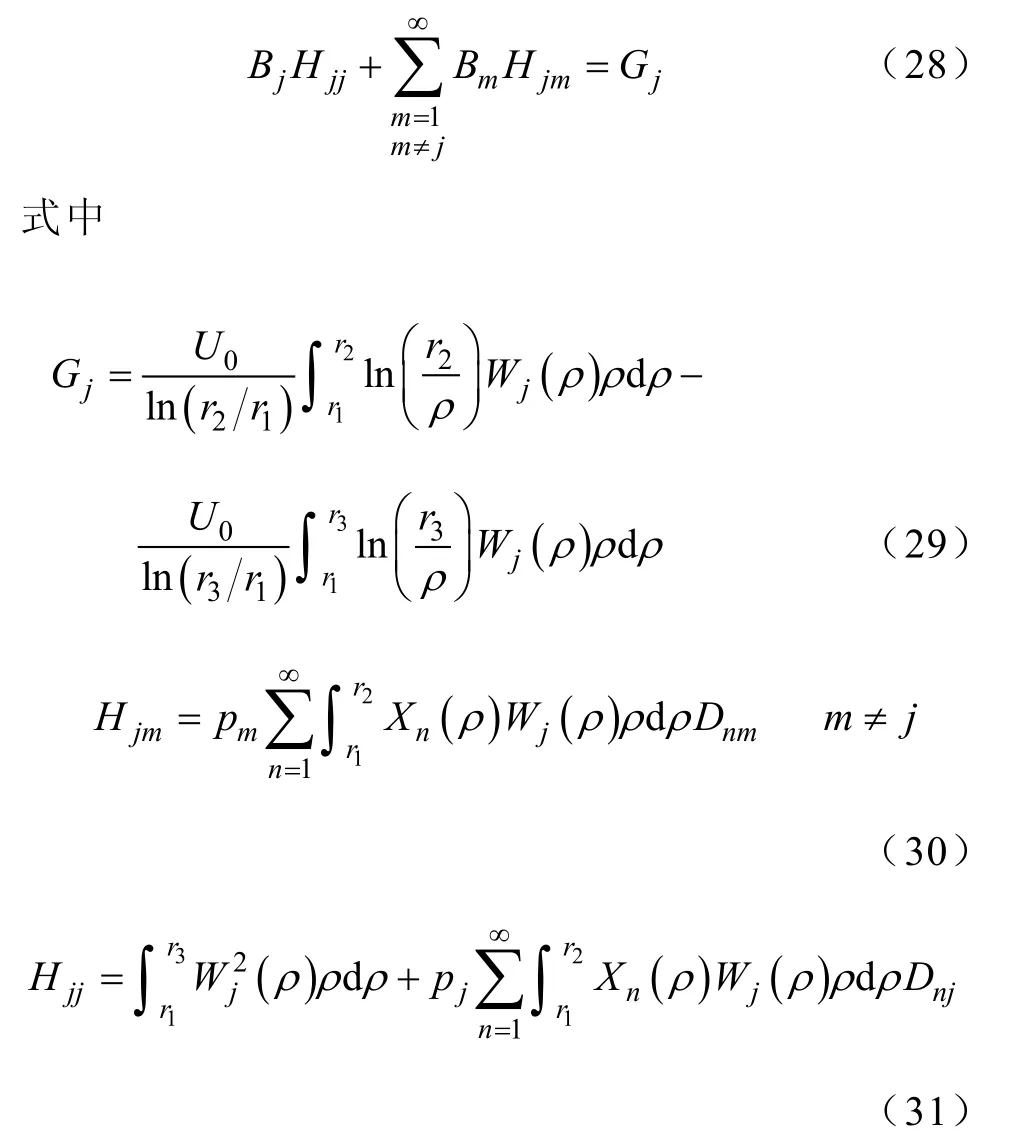
对j、m 分别从1 取到M,且m≠j,就构成了由M 个方程组成的方程组,并可解出系数Bm的值,进而由式(24)解出nA 的值。
补偿电容的值仅与结构突变处高阶模式的电位引起的电荷分布有关,即仅需考虑由 φA1和 φB1引起的导体上的电荷分布。
区域A 内由 φA1引起的内导体表面的电荷密度分布为
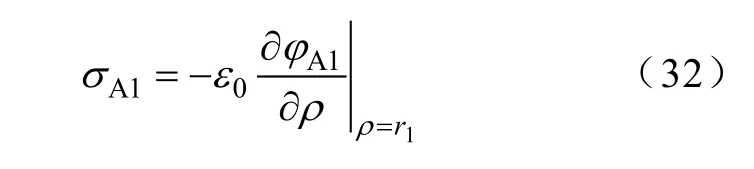
区域A 内由 φA1引起的内导体表面总电荷量为
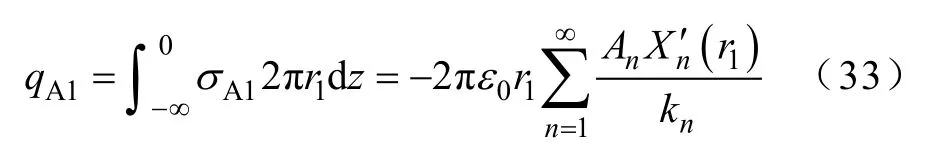
同理,区域B 内由 φB1引起的内导体表面的总电荷量为
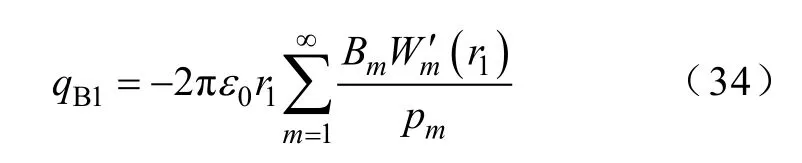
则由尺寸突变引起的该同轴结构的补偿电容为
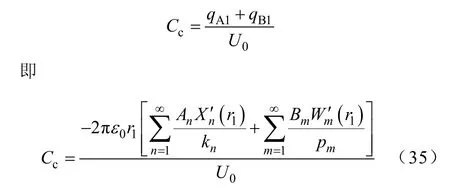
2 对比验证及规律分析
以变分原理为基础建立的有限元法[13]已被普遍推广并成功应用于电磁场工程问题等应用技术领域。本文利用Ansys 和Maxwell 两种有限元软件计算验证了上述公式的正确性。有限元计算模型如图3 所示。利用同轴结构的轴对称特性,画出二维轴面;模型的总长度L 远大于区域B 的外导体半径r3。在模型的左、右边界分别施加电场平行边界条件;内导体施加1V 电压,外导体电位为0。

图3 补偿电容的有限元计算模型Fig.3 Model in FEM for calculating the compensation capacitance
本文分别对比了“z=0,r1<ρ<r2线上的电位分布”和“内导体表面电场强度”,以验证本文公式在不同点上的计算结果与有限元结果一致,如图4、图5 所示。其中,计算模型的尺寸为r1=0.1m、r2=0.2m、r3=0.3m。由图4、图5 可见,图中的公式计算结果与有限元软件的计算结果的一致性很好,说明本文公式的正确性。
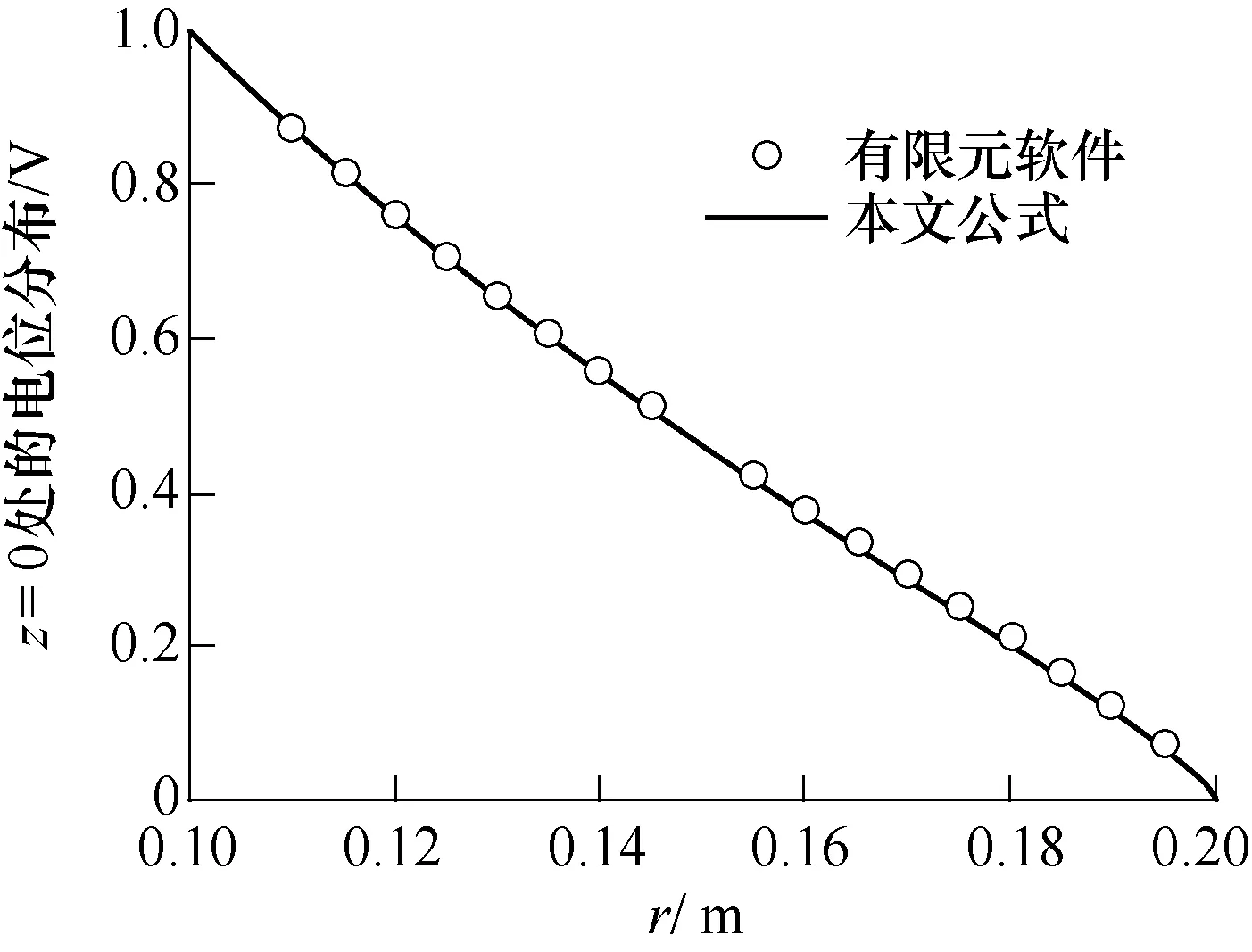
图4 z=0,r1<ρ<r2线上的电位分布的对比Fig.4 Comparison of potential distribution at z=0,r1<ρ<r2

图5 内导体表面电场强度的对比Fig.5 Comparison of electric field intensity at inner conductor surface
有限元计算模型的补偿电容Cd为
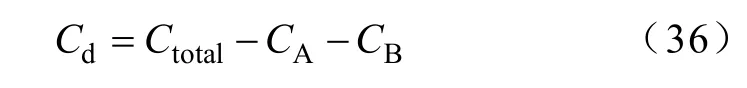
式中,Ctotal为内外导体间的总电容;CA、CB分别为均匀区域A、B 段的电容,利用区域A、B 的同轴结构单位长电容公式乘以长度计算。
文献[5]基于Schwarz-Christoffel(施瓦兹-克里斯多菲)变换[14],给出了平行平板结构的尺寸突变处的横向单位长度静态补偿电容的精确计算公式
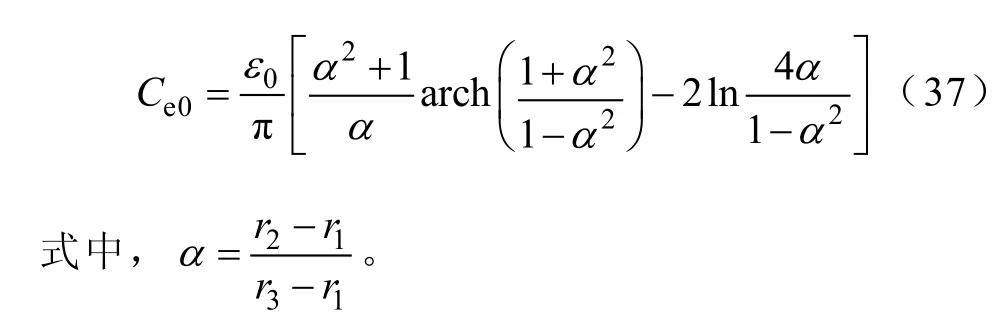
由式(37)乘以同轴结构内导体周长可近似应用于同轴结构半径突变处补偿电容的计算,即

图6 和图7 给出了不同半径取值下补偿电容的四种计算方法的对比结果。由图6 和图7 可见,本文计算模型与有限元软件的计算结果相对误差较小。近似公式与有限元软件的相对误差较大;且r2/r1越小,r3/r1越大,补偿电容的值越大。

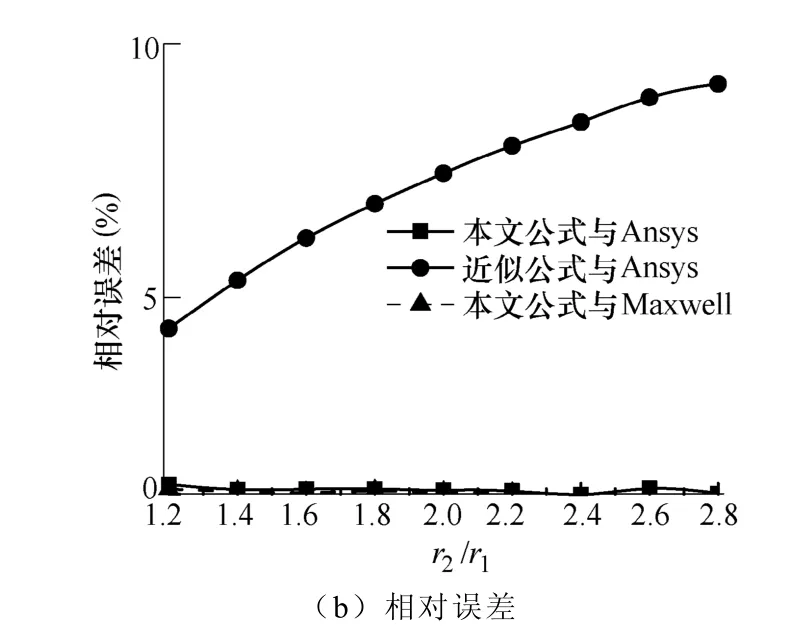
图6 r1=0.1m,r3=0.3m,不同r2/r1时补偿电容的对比Fig.6 Comparison of compensation capacitance value among different r2/r1with r1=0.1m and r3=0.3m
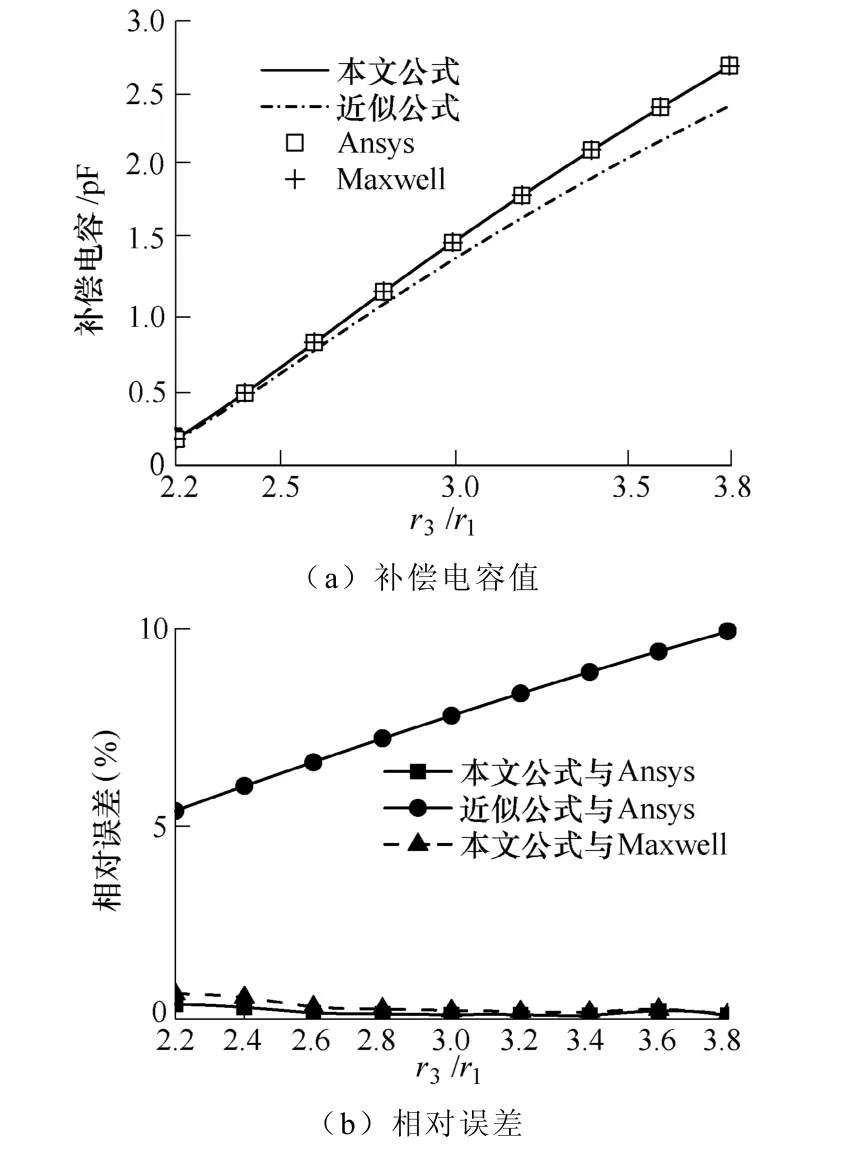
图7 r1=0.1m,r2=0.2m,不同r3/r1时补偿电容的对比Fig.7 Comparison of compensation capacitance value among different r3/r1with r1=0.1m and r2=0.2m
3 应用算例
为分析补偿电容对时域信号传输的影响,作了“有补偿电容”和“忽略补偿电容”时半径突变的同轴结构的终端电压的对比。基于EMTP[15,16]仿真平台的仿真模型如图8 所示。其中,计算模型的尺寸为r1=0.1m,r2=0.2m,r3=0.3m,区域A、B 的同轴线的长度均为1m。在区域B 的始端加上升时间为5ns、下降时间为50ns、幅值为10kV 的双指数函数信号源,仿真的时间步长为0.005ns。区域A 的终端接不同负载R,对比区域A 终端的电压。
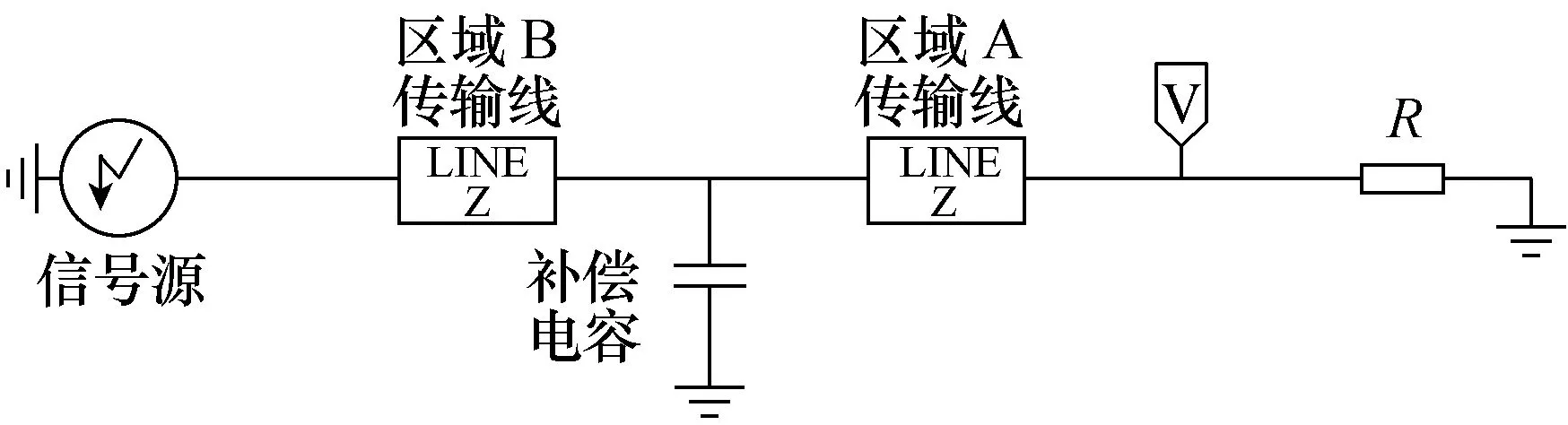
图8 EMTP 仿真模型Fig.8 Simulation model using EMTP
区域A 终端电压的对比结果如图9 所示。由图9 可见,当区域A 终端接匹配电阻时,台阶电容对时域信号的传输影响很小。当区域A 终端接1MΩ或0.1Ω电阻时,由于阻抗不匹配产生了信号的折反射,由图9b、图9c 可见,在多次折反射后,忽略补偿电容时的电压波形比有补偿电容时的电压波形超前。
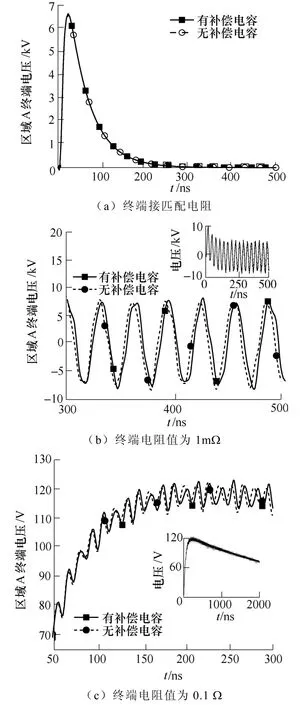
图9 补偿电容对时域信号传输的影响Fig.9 Comparison of influence of compensation capacitance to transmission of the time domain signal
4 结论
本文推导出同轴结构半径突变处静态补偿电容的精确计算模型,该模型计算简便,准确度高,计算结果与有限元软件的结果的相对误差不超过1%,也说明了本文计算模型的正确性;并且当负载不匹配时,相比考虑半径突变同轴结构等效电路的补偿电容时,忽略补偿电容时会产生信号超前。平行平板结构尺寸突变处静态补偿电容的精确公式近似应用于同轴结构时误差较大,在一些尺寸下甚至超过了10%;近似公式形式简单,缺点是准确度低。有限元软件能以较高的准确度求解复杂工程电磁问题,但是需要使用者能熟练、正确地使用软件。
[1]Marcuvitz N.Waveguide handbook[M].New York:Mcgraw-Hill,1951.
[2]Ramo S,Whinnery J R.Fields and waves in modern radio[M].New York:John Wiley &Sons,1953.
[3]Whinnery J R,Jamieson H W.Equivalent circuits for discontinuities in transmission lines[J].Proceedings of the IRE,1944,32(2):98-114.
[4]Whinnery J R,Jamieson H W,Robbins T E.Coaxial-line discontinuities[J].Proceedings of the IRE,1944,32(11):695-709.
[5]胡榕,崔翔,陈维江,等.特高压气体绝缘开关设备瞬态外壳电压特性的试验研究[J].中国电机工程学报,2014,34(29):5244-5258.Hu Rong,Cui Xiang,Chen Weijiang,et al.Experimental research on the characteristics of transient enclosure voltage in ultra high voltage gas insulated switchgear[J].Proceedings of the CSEE,2014,34(29):5244-5258.
[6]吴昊,李成榕,徐海瑞,等.用于VFTO 测量的GIS窗口式传感器[J].电工技术学报,2012,27(9):210-217.Wu Hao,Li Chengrong,Xu Hairui,et al.Method for measurement of VFTO based on GIS disk sensor[J].Transactions of China Electrotechnical Society,2012,27(9):210-217.
[7]孟涛,林莘,徐建源.分段电弧模型下VFTO 的计算与分析[J].电工技术学报,2010,25(9):69-73.Meng Tao,Lin Xin,Xu Jianyuan.Calculation of very fast transient over-voltage on the condition of segmental arcing model[J].Transactions of China Electrotechnical Society,2010,25(9):69-73.
[8]倪光正.工程电磁场原理[M].2 版.北京:高等教育出版社,2009.
[9]Harrington R F.Time-harmonic electromagnetic Fields[M].New York:Wiley-IEEE Press,2001.
[10]张善杰.矢量函数、圆柱函数和球函数[M].南京:南京大学出版社,2011.
[11]王泽忠,全玉生,卢斌先.工程电磁场[M].北京:清华大学出版社,2004.
[12]王竹溪,郭敦仁.特殊函数概论[M].北京:北京大学出版社,2012.
[13]胡仁喜,孙明礼.ANSYS13.0 电磁学有限元分析从入门到精通[M].北京:机械工业出版社,2011.
[14]龙非池,王慧.基于 Schwarz-Christoffel 变换的平板电容器电场电荷分布仿真[J].物理与工程,2007,17(6):25-27.Long Feichi,Wang Hui.Simulation on the distribution of electric field and charges of flat capacitor based on schwarz-christoffel transformation[J].Physics and Engineering,2007,17(6):25-27.
[15]吴文辉,曹祥麟.电力系统电磁暂态计算与 EMTP应用[M].北京:中国水利水电出版社,2012.
[16]杨琳,吴广宁,田晓菲.基于EMTP 的水平接地体冲击时-频特性分析[J].电工技术学报,2011,26(6):194-198.Yang Lin,Wu Guangning,Tian Xiaofei.Analysis of impulse characteristic grounding electrode in frequency and time domain based on EMTP[J].Transactions of China Electrotechnical Society,2011,26(6):194-198.

