接触网腕臂结构系统动力学分析
李少鹏,邓 洪,古晓东
(铁道第三勘察设计院集团有限公司电化电信处,天津 300251)
接触网腕臂结构系统动力学分析
李少鹏,邓 洪,古晓东
(铁道第三勘察设计院集团有限公司电化电信处,天津 300251)
根据实际工况建立接触网腕臂结构系统的有限元模型。利用有限元法对此模型进行受力分析,校核其静强度、静刚度。建立腕臂结构系统的动力学模型,通过模态分析得出模型的前10阶固有频率及振型,并通过谐响应分析计算在外载荷的影响下结构的共振频率。通过对腕臂结构系统的动力学分析,得出在外载荷作用下,整体结构系统不会发生共振现象,与实际工程项目相符,为工程实际提供理论支持。
接触网;腕臂结构;有限元法;固有频率;静力学分析;动力学分析
共振现象的发生会极大地降低结构的可靠性、螺栓螺母的防松以及受电弓的受流特性,在设计施工阶段应尽量避免[1]。高速列车受电弓在经过定位线夹的时候,会对腕臂结构系统造成冲击及振动,同时风载荷、接触线张力等外载荷的变化对接触网整个结构系统也会产生一定的影响。对接触网系统,正常行车的情况下,接触线垂直方向固有频率f在1 Hz左右[2]。目前鲜有腕臂支撑结构以及其与接触线之间的共振关系进行分析计算的研究,一般只依靠工作经验,没有理论支撑。国标中对此没有严格要求,该项往往被忽略,淡漠了结构的动态性能。
通过对腕臂结构系统进行模态分析、谐响应分析以及相关力学计算,对整体结构系统的动力学性能进行分析评估,验证模型与实际工况的符合程度。
1 结构静力学模型及特性分析
本文选用最不利工况,即下锚支的大限界腕臂结构系统作为分析对象。腕臂底座间距1.8 m,平腕臂总长4.1 m,且为钢腕臂结构。建立完整的SolidWorks实体模型,并对模型根据实际工况进行简化,完成有限元模型的转化。同时,有限元模型的腕臂和绝缘子用空间梁单元模拟,腕臂支撑用杆单元模拟[3,4]。图1为该腕臂结构系统的SolidWorks实体模型,图2为其ANSYS的有限元简化模型。
图1 腕臂结构系统实体模型
图2 腕臂结构系统有限元模型
实际工作状态中,考虑到接触线的张力、自重、风载荷、冰雪载荷以及下锚等引起的额外负载,对腕臂结构系统进行静力分析[5]。
本文由于旨在分析腕臂结构的整体受力情况,为了排除所有由于建模原因可能引起的局部应力使计算结果更符合工程实际,对结构衔接处的连接件(螺栓、定位环等)进行简化,以两点耦合的形式模拟铰接。同时由于绝缘子结构在建模时极容易引起局部应力,且其对计算结果影响极小,故将其简化为简单的圆柱体结构,但其质量、尺寸与真实情况相符。
采用基于铁木辛柯梁理论[6-7]的BEAM188梁单元进行模拟。本文的腕臂结构系统模型可简化为空间弹性支撑连续梁,根据相关文献,可导出连续梁单元有限元方程[8]:
节点位移函数为
(1)
式中vi——单元节点i处的位移;
θi——单元节点i处的转角;
vj——单元节点j处的位移;
θj——单元节点j处的转角;
l——i、j节点间的距离。
用节点位移表示的单元应力的关系为
(2)
式中,E为材料的弹性模量。
用节点位移表示单元的刚度矩阵为
(3)
考虑到[D]为与材料弹性模量有关的矩阵,且横截面惯性矩I=∬y2dydz,由虚功原理建立作用于单元上的节点力和节点位移之间的关系式即单元刚度方程为
(4)
式中,{F}e为单元节点力分量列阵,由此可解出[K]e。
综上所述,利用有限元法进行计算时的方程可描述为

(5)
式中,[K]为结构的总体刚度矩阵,由各单元的刚度矩阵组成;{δ}为节点位移列阵;{F}为节点载荷列阵。
通过将实际的位移边界条件带入式(5),解之可得单元的节点位移,再通过单元特性分析建立的关系式,即可求得所需应力、应变。
本文通过ANSYS有限元计算软件对模型进行强度、静刚度分析计算,结果如图3所示。
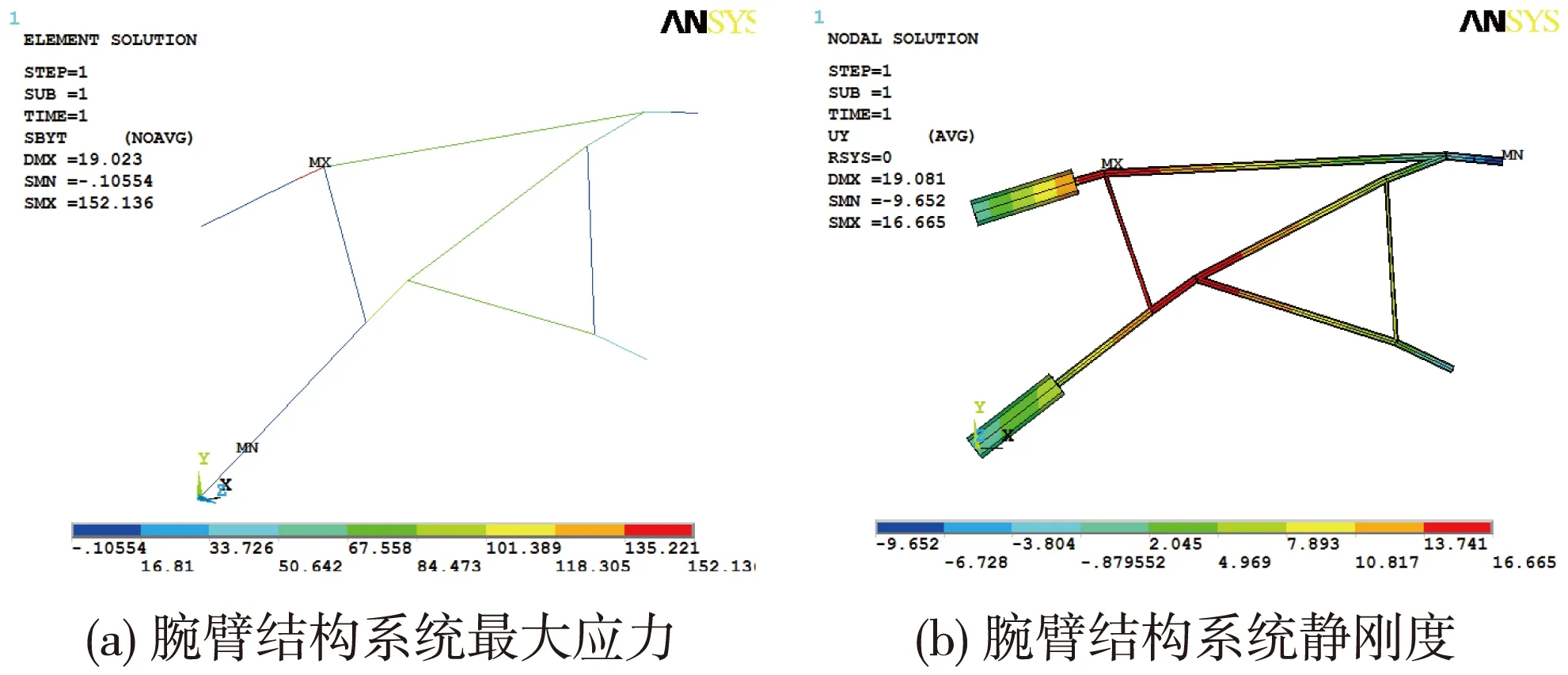
图3 腕臂结构系统分析
由图3可知,腕臂结构系统的最大应力出现在平腕臂与腕臂支撑的连接处,其值为152.13 MPa。由于为钢腕臂结构,其材料许用应力为245 MPa,满足设计要求。最大挠度出现在平腕臂与支撑连接处,其值为16.665 mm。设计规范中要求挠度不能大于腕臂长度的0.7%,同样满足设计要求[9]。
2 结构动力学模型及动力学特性分析
结构系统的动力学有限元方程为[10-12]
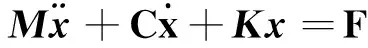
(6)

以腕臂结构系统的有限元模型为例,通过有限元法对其进行模态分析和谐响应分析计算其模态及响应。
进行模态分析时,视结构为不受外力作用的自由振动系统,且由于阻尼对结构的固有频率和振型影响不大,所以可按无阻尼自由振动情况求解固有频率和振型。其振动方程为
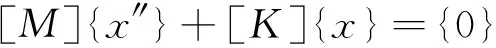
(7)
若将弹性体的自由振动分解为一系列简谐振动的叠加,则方程(7)的解可设为
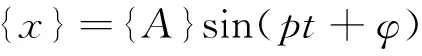
(8)
式中,p为角频率;φ为初相角;{A}为非零振幅列阵。
将式(8)代入式(7)可以求解出结构固有频率及振型的公式
(9)
对该模型进行模态分析,得到系统前10阶固有频率如表1所示。第1、4、5、7、10阶固有频率对应的主振型为结构沿列车行驶方向的水平振动。第2阶固有频率对应的主振型反映了结构沿平腕臂方向的扭转振动。第3、6、8、9阶的主振型反映了结构在竖直面的垂直振动。由于可将腕臂结构看作是简易的桁架系统,其前10阶固有频率及振型主要取决于腕臂的扭转及弯曲刚度。
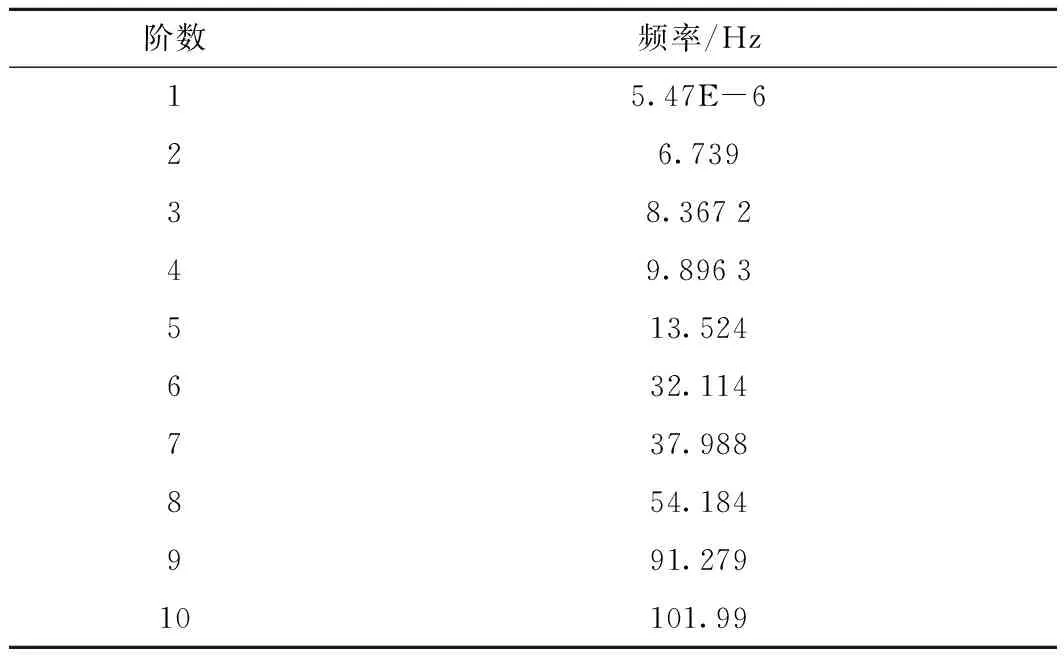
表1 腕臂结构系统前10阶固有频率
利用ANSYS软件对结构进行谐响应分析,找出在外载荷作用下(尤其是受电弓经过的瞬间、风载荷和接触线张力变化)对该结构动态性能影响最大的振动频率。在不同激振频率的动载荷作用下,腕臂系统最大的竖直位移点以及锚支定位卡子垂直方向的位移响应最大峰值均出现在第3阶模态,如图4、图5所示。故第3阶模态最易引起该结构的共振。对于正常工况下的接触线垂直方向固有频率为1 Hz左右。本例腕臂结构在垂直方向的固有频率为8.367 2 Hz。可见不会引起整体腕臂结构系统的共振,满足设计要求。
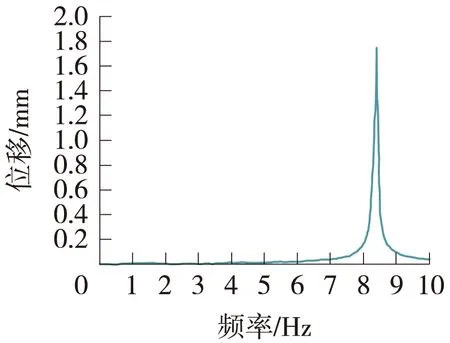
图4 最大竖直位移点垂直方向位移响应
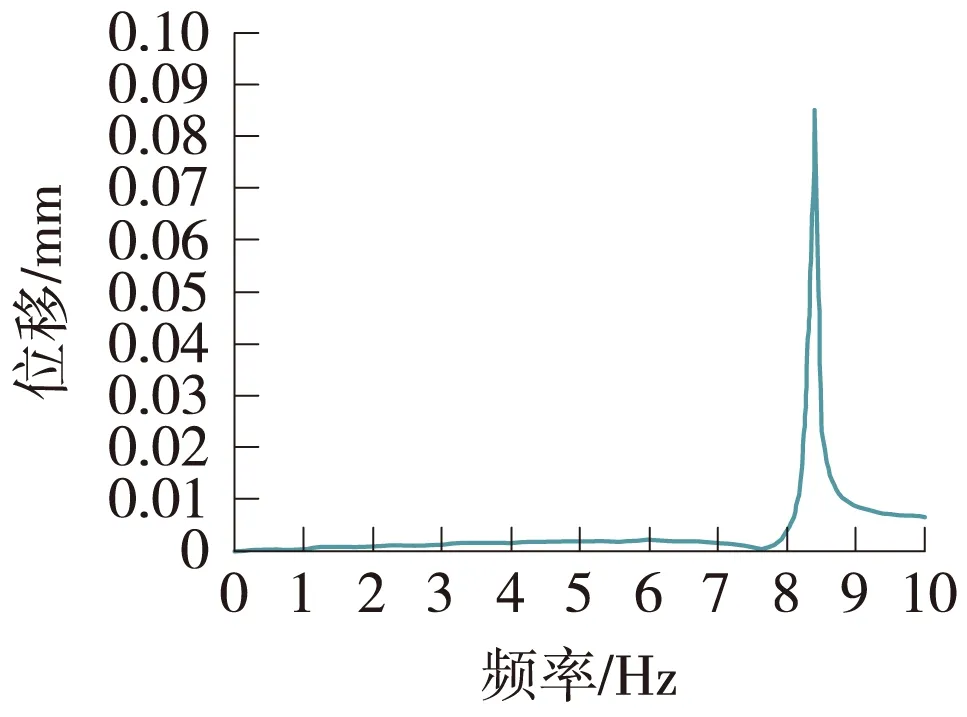
图5 锚支定位卡子垂直方向位移响应
3 结论
根据工程实际,建立了腕臂结构系统的实体模型和有限元模型。通过对模型的分析计算,校核了结构系统的静强度、静刚度,并对外载荷作用下的结构系统进行了动力学分析。通过模态分析以及谐响应分析确定了结构的固有频率。由以上计算可得,本文所建立模型的静强度、静刚度满足使用要求,并且在外载荷(接触线张力、受电弓、风载荷等)作用下不会发生影响整体可靠性的共振现象,与实际情况相符,为实际工程项目提供了理论支持。同时,通过本文的分析计算,也可得出结构振动的基本形式,对螺栓螺母的防松研究有一定的指导意义。
[1] 刘长利.强侧风下接触网响应特性及弓网运行安全分析[J].铁道标准设计,2013(2):105-109.
[2] 刘长利.高速铁路接触网低频振动及零部件防松技术分析[J].铁道标准设计,2014(10):113-116.
[3] 于兰峰,王金诺.塔式起重机结构系统动态优化设计[J].西南交通大学学报,2007,42(2):206-210.
[4] 刘峰涛.接触网腕臂支持结构的仿真分析[J].电气化铁道,2004(6):19-25.
[5] 李保华.基于有限元的腕臂结构静动态特性研究[D].成都:西南交通大学,2009.
[6] 蒋纯志,金桂,陈亚琦.等截面铁木辛柯梁的分布传递函数方法[J].湖南科技学院学报,2009,30(8):50-53.
[7] 金晶,邢誉峰.铁木辛柯梁固有振动频率的边界元解法[J].北京航空航天大学学报,2012,38(7):976.
[8] 成思源.有限元法的方法论[J].重庆大学学报:社会科学版,2001,7(4):61-63.
[9] 常国安,彭昶.京沪线电气化工程接触网腕臂计算分析[J].电气化铁道,2006(2):26-28.
[10]张卫华,沈志云.接触网动态研究[J].铁道学报,1991(4):26-33.
[11]许佳.梁结构振动响应的小波有限元法实现及应用研究[D].苏州:苏州大学,2012.
Dynamic Analysis of Cantilever Structure of OCS
LI Shao-peng, DENG Hong, GU Xiao-dong
(Department of Electrification & Telecommunications, The Third Railway Survey and Design Institute Group Corporation, Tianjin 300251, China)
A finite element model of cantilever structure is created based on engineering practices. Static analysis is conducted with finite element method to test the model’s strength and stiffness. Then a dynamic model is established and modal analysis is conducted to get the first ten natural frequencies and corresponding modes. Resonance frequency is obtained through harmonic response analysis under the influence of external load. Finally, conclusions are made that the overall structure is not subject to resonance vibration and complies with engineering actuality, which provides theoretical support to engineering practice.
OCS; Cantilever structure; Finite element method; Nature frequency; Static analysis; Dynamic analysis
2015-04-07;
2015-05-06
李少鹏(1988—),男,助理工程师,2014年毕业于西南交通大学机械设计及理论专业,工学硕士,E-mail:liseanh@163.com。
1004-2954(2015)11-0135-03
U225
A
10.13238/j.issn.1004-2954.2015.11.032

