A review of studies of mechanism and prediction of tip vortex cavitation inception*
ZHANG Ling-xin (张凌新), ZHANG Na (张娜), PENG Xiao-xing (彭晓星), WANG Ben-long (王本龙),SHAO Xue-ming (邵雪明)
1. State Key Laboratory of Fluid Power Transmission and Control, Department of Mechanics, Zhejiang University, Hangzhou 310027, China, E-mail: zhanglingxin@zju.edu.cn
2. China Ship Scientific Research Center, Wuxi 214082, China
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240,China
A review of studies of mechanism and prediction of tip vortex cavitation inception*
ZHANG Ling-xin (张凌新)1, ZHANG Na (张娜)1, PENG Xiao-xing (彭晓星)2, WANG Ben-long (王本龙)3,SHAO Xue-ming (邵雪明)1
1. State Key Laboratory of Fluid Power Transmission and Control, Department of Mechanics, Zhejiang University, Hangzhou 310027, China, E-mail: zhanglingxin@zju.edu.cn
2. China Ship Scientific Research Center, Wuxi 214082, China
3. School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai 200240,China
The inception of the tip vortex cavitation (TVC) is a very important problem in cavitation researches. The study of the mechanism of the TVC inception is not only conducive to its prediction, but also helps to suppress or suspend the occurrence of cavitation. In this paper, the research progresses on the TVC inception including theoretical, experimental and numerical studies mainly in the last two decades are reviewed. It is shown that the TVC inception is affected by complicated factors, such as the water quality, the average pressure and the fluctuating pressure. In the scaling law for the determination of the TVC inception, all these factors are considered. To precisely describe the scaling law, more investigations are needed to understand the effects of the water quality and the fluctuating pressure.
tip vortex, cavitation, inception, scaling law
Introduction
When a nucleus is entrained into the vortex core where the pressure is below a certain critical value, it will grow up and cavitate to become a visible slender bubble. The break-up of the TVC radiates a bursting noise and leads to erosion of the rudder behind the propeller. Typically, the TVC appears earliest on a real ship among all types of cavitation. The noise caused by the TVC will do harm to the acoustic stealthy performance of the ship. In order to suppress or suspend its inception there is an urgent need to accurately understand the detailed flow field around the tip.
A brief review of theoretical, experimental and numerical studies is presented in this paper. The former two concern traditional methods and were closely related to each other in the early days. However, it is still challenging to obtain accurate measurements of the cavitating flow because it is unstable and dynamic. An alternative approach for studying this problem is the high-resolution numerical calculation, which can provide some insight into the detailed process of the TVC.
1. Theoretical study
Unlike other types of cavitation, the TVC occurs in the vortex flow in the vicinity of the tip[1-4]. Of great interest to this issue is the vortex structure. In an ideal finite vortex model, the whole region can be divided into two parts, the core and the ring-form outer region. Rankine, Burgers et al. proposed their respective vortex models[1]. The distributions of the velocity and the pressure in the vortex flow are specified through the strength and the radius of the vortex core. The velocity distribution and the lowest pressure induced by the Burgers model[1]are as follows:

The occurrence of cavitation is related to the local pressure. The vortex cavitation first occurs in the vortex core due to its lowest pressure. However, since the tip vortex generated by the propeller blade is not an ideal line vortex, the strength and the radius of the vortex core are non-uniform, as illustrated in Fig.1.
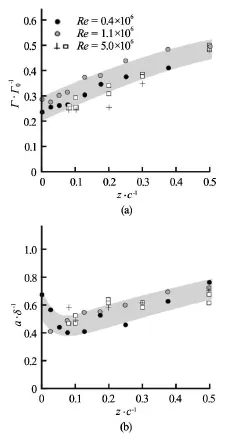
Fig.1 Variations of vortex strength and vortex core radius with the downstream distance[3]
The lowest pressure is not at the tip but at a down-stream location close to the tip, as shown in Fig.2. The minimum pressure is affected not only by the flow characters but also by the geometry such as the blade tip skewness and the contour of the blade. Fortunately, the minimum pressure is still in the same order as the pressure in the whole vortex core. It therefore can be described by the flow characters.

Fig.2 The inception location of TVC[4]
According to ideal vortex models, the lowest pressure is specified by the vortex flow strength and the radius of the vortex core. Fruman et al.[3]and Boulon et al.[5]measured the distribution of the vortex flow on the hydrofoils under various flow conditions. They found that the vortex strength is closely related to the load coefficient of the hydrofoil. According to the measurement of the vortex flow on different 3-D hydrofoils, the radius of the vortex core is found proportional to the thickness of the boundary layer on the hydrofoil[6,7]. Furthermore, they analyzed the relationship between the radius of the vortex core and the Reynolds numbers. Based on these investigations the following scaling law with nondimensional parameters is established to predict the TVC inception number[8-10]
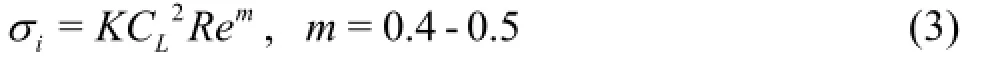
This scaling law can help us to understand the main factors with respect to the TVC inception. However,K andmare not universal parameters, especially, the constantK , which varies between 0.035 and 0.073[11].
According to recent investigations, there are probably three factors that affect the parameters in the scaling law:
(1) The local tip vortex interacts with the leading-edge detached vortices, the trailing-edge detached vortices and other sets of vortices.
(2) The minimum pressure is affected by the local transient fluctuating pressure in the vortex flow.
(3) The cavitation inception is sensitive to the size distribution of the nuclei in the free stream.
Maines and Arndt[9]identified the interaction between the boundary layer and the tip vortex on diffe-rent NACA-type cross sections through the oil visualization technique, as shown in Fig.3. They found that the interaction on the hydrofoil is stronger if its lift coefficient is lower. Hsiao and Chahine[12]simulated the interaction between two line vortices of different strength, as shown in Fig.4. The results show that the axial velocity increases significantly as the weak vortex is wrapped into the strong vortex. The pressure in the vortex core is also found to be lower. However,there are relatively few studies of the vortex interaction on typical hydrofoils or propellers, especially,the influences of other sets of vortices on the tip vortex. In addition, the boundary layer separations could be different for different Reynolds numbers. Therefore,the conclusions from the model test and the simulation are still questionable with respect to the real ship applications.

Fig.3 Interaction between the detached vortices and the vortex flow[9]
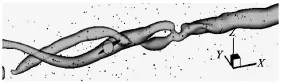
Fig.4 Interaction between two line vortices[12]
So far, the second and third factors are accepted by many scholars. Arndt[11]improved the scaling law by separating the factors into three parts: the average vortex flow, the pressure fluctuation intensity and the size distribution of the nuclei. Finally the modified scaling law can be written as

where the first and second terms reflect the effects of the average pressure in the vortex core and the local pressure fluctuation. The last term incorporates the tensile strength of the liquid related to the size distribution of the nuclei. The influence of the pressure fluctuation and the size distribution of the nuclei is currently still under study. Some results will be presented in the next two sections.
The inception of the TVC is controlled by a complex physical process, in which both the flow parameters and the water quality play important roles. Many attempts have been made to establish the basic scaling law, to account for the effect of the Reynolds number and the load coefficient. In the new scaling law, proposed by Arndt[11], the effects of other factors are considered, such as the pressure fluctuation and the water quality. However, the roles of these factors are still far from very clear.
2. Experimental study
There are two ways to detect the occurrence of the TVC. One is the optical detection such as the stroboscope observation and the high-speed camera observation, based on the visible cavity growing from tiny nuclei. The other is the acoustic detection[13]. When tiny cavities are moving into the vortex flow, a great pressure variation can be observed due to their evolution, with strong noises. Thus, the TVC inception can be predicted by capturing the acoustic signal generated from the pressure fluctuation.
To investigate the cavitation mechanism it is essential to measure the cavitation pattern and the induced noise simultaneously. Pereira et al.[14]conducted this measurement on the propeller in a uniform incoming flow. The cavitation volume was recorded by a high-speed camera to find the relationship between the volume variation and the noise strength. Using the high-speed video observation and the hydrophone,Choi and Chahine[15]recorded the inception, the growth and the collapse of the TVC and the radiated noises in the hydrofoil wake. According to their results,when a slender cavitation is collapsing, the amplitude of noises is nearly four times as one during incepting. Further, Maines and Arndt[9]used the high-speed video observation to study the TVC singing of the hydrofoil. By analyzing the process photograph and the acoustic signal they have established the inception condition of the TVC singing.
With the developments of various testing technologies such as the two-dimensional laser Doppler velocimetry (LDV) and the particle imaging velocimetry(PIV), numerous measurements of the TVC flow field were made for a series of hydrofoils having different geometries[3,16-18]. They aim to determine the effects of various factors, especially, the Reynolds number and the size of the nuclei, upon the TVC occurrence process. In recent decades, the development of the high-resolution velocimetry equipment and the observation technology makes it possible to directly determine the TVC flow field[19-22].
Up to now, the detection technique of the small-scale structure and the turbulence pulsation is still on the way of developing. Arndt and Keller[23]measured the pressure fluctuation inside a tip vortex around the elliptical hydrofoil by the LDV and the holography. It is indicated that the magnitude of the fluctuation in the low-pressure region is enough to affect the inception of the TVC. Ran and Katz[24]found that the cavitation often firstly occurs in a small-scale vortical structure,therefore, the inception cavitation number is larger than the estimated value. The same conclusion was reached by Gopalan et al.[25]. Green and Acosta[26]showed that the magnitude of the pressure fluctuation is very high in the vortex core. However Fruman[8]insisted that Green's data should be taken at the location more than one chord length downstream from the tip and hence the magnitude may be overestimated. The fluctuation effect was studied indirectly by Korkut and Atlar[27]. To obtain the relationship between the turbulence and the TVC inception they generated an artificial disturbance upstream. Due to the lack of direct proofs from experimental data, it is still unable to quantify the impact of the unsteady pulsating effects.
The usual measurement methods for the nuclei include the venturi tube technique, the holography and the laser interferometric technique[28]. Peng et al.[28],Briancon-Marjollet and Merle[17]studied the effect of the water quality on the TVC growth. Different size distributions of the nuclei lead to totally different inception cavitation numbers. Moreover, the initial position of the TVC is very sensitive to the size distribution of the nuclei[23]. With a high air content, the position where the cavitation initially occurs is very close to the tip of the hydrofoil. Once captured, the nucleus develops downstream around the vortex axis. In the case of a low air content, the cavitation incepts at a lower cavitation number and at the position away from the tip.
To predict the inception cavitation number, Arndt and Maines[29]took the tensile strength of the liquid as an independent factor into account. As shown in Eq.(4), the third term is referred to the water quality. It is not successful to quantify this effect due to the fact that not only the initial static condition of the nuclei but also the dynamic flow condition affects the tensile strength. Comparatively, the designed cavitation number based on numerous researches is stable. To overcome the uncertainty due to the different water quality,the designed cavitation number is adopted in a strong water (water with a low air content and small size nuclei), while the inception number is used in a weak water (water with a high air content and large size nuclei)[30].
Most studies of cavitation are based on model tests. Because the water quality and the Reynolds number are quite different between the model test and the full scale ship, the onboard cavitation measurement is therefore very important to scale the model test results as well as to validate the numerical results. The difficulties come from the fact that the cavitation of the propeller blade changes with its rotation, and the observation has to be done through the ship hull in a very limited bottom space in the ship stern[31,32]. Currently, there are two ways to do that[33], namely, through windows or using endoscope. The location of windows are opened on the ship hull at selected locations for good comprehensive observations. Using endoscope is much easier to install than using windows,and a movable view is one of the advantages. So it is now extensively used in the onboard cavitation observation.
The developments of new techniques make it possible to observe and measure the detailed flow field around the tip. The measurement of the average field becomes just a basic skill to investigate the inception of the TVC. Although the measurement of the turbulence fluctuation in the vortex flow is a very interesting issue, a quantitative description of the pressure fluctuation is still few and far between. The water quality can be measured and described by the size distribution of the initial nuclei, but the initial size distribution is not easy to adjust according to the user requirements.
3. Numerical simulations
In previous studies, the occurrence of the TVC is predicted by some simple vortex models. The linear ranking vortex model was used to generate a tip cavitating flow. The vortex strength is determined by the model testes or the potential flow method in an analysis of the minimum inside pressure. By now, the prediction is commonly conducted by combining the RANS or LES method with the bubble dynamics. With the development of the CFD and the computational tools, the numerical simulation plays an increasingly important role in the investigation of the TVC. The major trends in the numerical simulation fall into three directions, the high-resolution simulation of the tip vortex flow, the spherical bubble dynamics simulation and the non-spherical bubble dynamics.
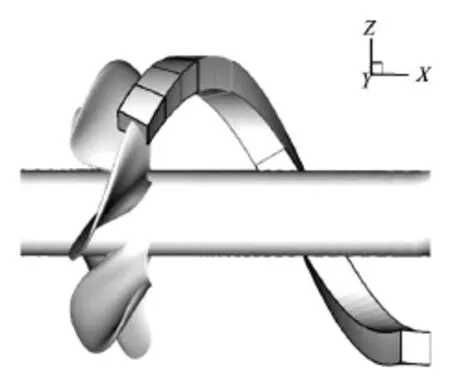
Fig.5 The sketch of local grid refinement of the propeller tip vicinity[34]
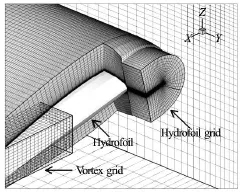
Fig.6 The detailed view of the chimera grid system in the tip region[35]
Owing to the tiny size and the large pressure gradient in the vortex core, it is difficult to simulate the tip vortex accurately. Attempts to resolve the dilemma come up with two useful methods, including the high grid resolution in the vortex core and the proper turbulent model for unsteady vortex flows. Rayleigh established the spherical bubble model,which describes the evolution of the bubble radius[42]. It is a one-way coupled method, which assumes that the bubble does not interact with the carrier phase. The nonspherical bubble model is a proper improvement over the spherical bubble model. The interaction between the bubble and the flow field is considered.
On the basis of the single bubble dynamics, the modified surface-averaged pressure (SAP) bubble dynamics is developed to capture the feature of the tip vortex flow from the flow field solved by the RANS or the LES[43,44]. The Euler-Lagrange approach is applied to simulate the evolution, the scale effect and the acoustic pressure of the cavitating flow. The mathematical model contains two parts. The flow field is determined by the Eulerian approach while the nuclei are tracked by the Lagrange approach. The equations of a bubble can be written as:

Promising results were obtained by a multiple optimization of the high grid resolution[34,35]. The typical refined grids for the simulation of the tip vortex are shown in Fig.5 and Fig.6. The minimum number of grid points is about 15 grid points across the radius of the vortex core, which is confirmed through extensive numerical studies[36]. According to the position of the lowest pressure obtained by preliminary calculations, the grid in the tip vortex core is refined adaptively and aligned with the tip vortex centerline.
The RANS model is widely used in the calculations of turbulent cavitating flows[37]. With the model,the averaged quantities are obtained, ignoring the small-scale turbulence structure. Mompean et al.[38]suggested that the non-linear RANS model is more appropriate in the simulation of the vortex flow. Of course, the method of a higher resolution can better help to study the influence of pressure fluctuations on the TVC. Schmidt et al.[39]obtained the pressure fluctuations in the order of 10-6s by applying a high resolution of 10-8s in time. The instantaneous peak pressure ranges from O (1)bar to O(100)bar. The value and the position of the lowest pressure simulated using the DNS by Hsiao and Chahine[40]were in agreement with the experimental results, which proved the significant effect of the pressure fluctuations on the cavitation occurrence.However, the DNS is only applied in low Reynolds number flows for the limitation of the computational capability. As a compromise,it is economical to utilize the LES method[41].
To simulate the bubble dynamics and predict the TVC inception, the nuclei are released in the upstream of the tip vortex flow fields. There are two models to study the dynamics of bubbles, the spherical bubble model and the nonspherical bubble dynamics model.
Equation of motion (5) describes the bubble's trajectory and Eq.(6) describes the time-varying radius of the bubble. The equations of the SAP method differ from the traditional equations in two aspects. On one hand, the additional term is introduced for the slip velocity between the bubble and the carrier phase. On the other hand,pencounteris the averaged pressure on the bubble surface in all directions. If the size of the bubble is relatively smaller than that of the vortex core,the pressure gradient near the bubble is very small and can be ignored. Otherwise, it is necessary to average the ambient pressure over the bubble surface.pencounteris determined by an interpolation algorithm from the values on the background grid. It is simple to simulate the dynamics of the bubbles with the random size distribution of the nuclei, as shown in Fig.7. The cavitation inception law numerically investigated by Hsiao and Chahine[34]is close to the experimental measurements by Fruman et al.[45]. Yakubov et al.[46,47]also found that the numerical calculation can give the same predictions as those obtained by the experiment if they have the same size distributions of the nuclei.
Since in the spherical bubble models, the stretch and the deformation of bubbles can not be taken into account, Choi et al.[48]and Chahine et al.[49]employed the direct numerical simulation in calculating the dy-namics of the deformable bubbles. Figure 8 shows their results: the bubbles near the vortex axis are stretched to be slender, and then break with the back jet along the axis. Due to the drastic volume change, the intense acoustic radiation is produced. In this process,the break of the bubble and the axial back jet both contribute to the strong acoustic radiation, particularly,that of the axial back jet. Chahine's group even put forward a kind of split spherical bubble model, in which one bubble is expected to break up into two when the bubble radius reaches its critical value.

Fig.7 The nuclei distribution in free stream[41]

Fig.8 The deformation process of the bubble in vortex flow[47]
These two kinds of bubble models have their own advantages and disadvantages. The spherical bubble model reduces the computational burden and can be used to calculate the inception process of the bubble. To quantitatively study the effect of the water quality, a random size distribution of the nuclei is generated upstream. However, only the influence of the carrier phase on the bubble is taken into consideration. When the bubble size exceeds the scale of the vortex core, there is a marked computational deviation. The non-spherical bubble model can account for the bubble deformation and the bubble/flow interaction. In spite of a great improvement, it is limited in applications. Considering the huge scale variations, the spherical model is a proper approach to study the growth of the nuclei at the first stage. Then, the DNS method is employed to investigate the deformation of bubbles and the interaction between the bubble and the flow. In addition, the effect of the bubble-bubble interaction in the multi-bubble system should not be ignored according to the study of Zhang et al.[50].
There is still another issue about the interaction between the turbulence fluctuation and the motion of bubbles. Even though the magnitude of the pressure fluctuations in the vortex is large according to the experimental and numerical studies mentioned previously, the time scale of the fluctuations is not clear so far. If the duration of the pressure fluctuations is far smaller than the characteristic time of the bubble, the pressure fluctuations do not seem to be responsible for the occurrence of the tip vortex. Until now the transient turbulent feature is not well understood as well as the response of the nuclei subject to the pulsating field.
In order to understand the detailed features of the non-cavitating/cavitating tip vortex, it seems necessary to resort to high-resolution numerical calculations. The DES is a feasible turbulence model for the simulation of the tip vortex flow. As noted above, the spherical bubble model is a simple but efficient approach in studying the inception process of the TVC. The non-spherical bubble model, combined with the spherical bubble model, is mainly used to study the detailed deformation process of the cavitation bubble in the vortex.
4. Conclusions
This paper reviews the progresses of studies of the inception and the prediction of the TVC in recent two decades. The scaling law, which is used to determine the inception cavitation number, is established. The basic scaling law accounts for the effect of the Reynolds number and the lift coefficient. Meanwhile,the consideration of other complicated factors might improve the accuracy of the scaling law. Among these factors, the effect of the size distribution of the nuclei attracts much attention, particularly in numerical studies. The effects of other factors such as the vortex/ vortex interaction and the turbulent fluctuation are still far from clear.
Further improvement of the scaling law may rely on the systematic investigations of the detailed flow field around the tip. The following topics might be necessary to be studied:
(1) The high-resolution measurement and numerical calculation of the tip vortex flow.
(2) The magnitude and the frequency of the pressure fluctuation in the tip vortex flow.
(3) The response of the nuclei to the transient turbulent flow around the tip.
(4) The relationship between the tensile strength and the size of the nuclei.
References
[1]FRANC J. H., MICHEL J. M. Fundamentals of cavitation[M]. New York, USA: Kluwer Academic Publishers, 2004.
[2]STINEBRING D. R., FARRELL K. J. and BILLET M. L. The structure of a three-dimensional tip vortex at high Reynolds numbers[J]. Journal of Fluids Engineering, 1991, 113(3): 496-503.
[3]FRUMAN D. H., DUGUE C. and PAUCHET A. et al. Tip vortex roll-up and cavitation[C]. 19th Symposium on Naval Hydrodynamics. Seoul, Korea, 1992, 24-28.[4]MAINES B. H., ARNDT R. Viscous effects on tip vortex cavitation[C]. 4th Proceedings of Internatioanl Symposium on Cavitation Inception. New York, USA,1993.
[5]BOULON O., FRANC J. P. and MICHEL J. M. Tip vortex cavitation on an oscillating hydrofoil[J]. Journal of Fluids Engineering, 1997, 119(4): 752-758.
[6]KATZ J., GALDO J. Effect of roughness on roll-up of tip vortices on a rectangular hydrofoil[J]. Journal of Aircraft, 1989, 26(3): 247-253.
[7]MCALISTER K. W., TAKAHASHI R. K. Wing pressure and trailing vortex measurements[R]. Moffett Field, California, USA, NASA TP-3151, 1991.
[8]FRUMAN D. H. Recent progress in the understanding and prediction of tip vortex on a rectangular hydrofoil[C]. 2th International Symposium on Cavitation. Tokyo, Japan, 1994, 19-29.
[9]MAINES B. H., ARNDT R. Tip vortex formation and cavitation[J]. Journal of Fluids Engineering, 1997,119(2): 413-419.
[10]KELLER A. P., ROTT H. K. Scale effects on tip vortex cavitation inception[C]. Proceedings of JSME Fluids Engineering Symposium. San Franscisco, USA, 1999,FEDSM 99-7298.
[11]ARNDT R. Cavitation in vortical flows[J]. Annual Review of Fluid Mechanics, 2002, 34(1): 143-175.
[12]HSIAO C. T., CHAHINE G. L. Effect of vortex/vortex interaction on bubble dynamics and cavitation noise[C]. 5th International Symposium on Cavitation. Osaka,Japan, 2003, 1-4.
[13]CHEN Yi-hong, ZHOU Wei-xin and SHI Xiao-jun et al. Investigation of the nuclei population distribution measurement using acoustic inverse method[J]. Journal of Ship Mechanics, 2010, 14(8): 945-950(in Chinese).
[14]PEREIRA F., SALVATORE F. and DI F. F. et al. Experimental investigation of a cavitation propeller in non-uniform inflow[C]. 25th Symposium on Naval Hydrodynamics. St. John's, Canada, 2004.
[15]CHOI J. K., CHAHINE G. L. Noise due to extreme bubble deformation near inception of tip vortex cavitation[J]. Physics of Fluids, 2004, 16(7): 2411-2418.
[16]ARNDT R., MAINES B. H. Viscous effects in tip vortex cavitation and nucleation[C]. 20th Symposium on Naval Hydrodynamic. Santa Barbara, Canada, 1994.
[17]BRIANCON-MARJOLLET L., MERLE L. Inception development and noise of a tip vortex cavitation[C]. 21th Symposium on Naval Hydrodynamics. Trondheim, Norway, 1996, 851-864.
[18]YANG Zhi-ming, DING Yu-jian. Comparison of results on cavitation inception for checking the scale effects[J]. Journal of Hydrodynamics, Ser. B, 2004, 16(3):308-311.
[19]JESSUP A. Tip-leakage vortex inception on a ducted rotor[C]. 4th International Symposium on Cavitation. Pasadena, Canada, 2001.
[20]WOSNIK M., MILOSEVIC I. Time-resolved particle image velocimetry (TR-PIV) in ventilated and naturally cavitating flows[C]. 6th International Symposium on Particle Image Velocimetry. Pasadena, Canada,2005.
[21]ZHANG Rong-sheng, ZHENG Yuan and CHENG Yun-shan. Study of measuring micro-bubble diameter[J]. Journal of Experiments in Fluid Mechanics,2005, 19(2): 91-95(in Chinese).
[22]FOETH E. J., TERWISGA T. Applying time-resolved PIV to attached cavitation[C]. 6th International Symposium on Cavitation. Wageningen, The Netherlands,2006.
[23]ARNDT R., KELLER A. P. Water quality effects on cavitation inception in a trailing vortex[J]. Journal of Fluids Engineering, 1992, 114(3): 430-438.
[24]RAN B., KATZ J. Pressure fluctuations and their effect on cavitation inception within water jets[J]. Journal of Fluid Mechanics, 1994, 262: 223-263.
[25]GOPALAN S., KATZ J. and KNIO O. The flow structure in the near field of jets and its effect on cavitation inception[J]. Journal of Fluid Mechanics, 1999, 398:1-43.
[26]GREEN S. I., ACOSTA A. J. Unsteady flow in trailing vortices[J]. Journal of Fluid Mechanics, 1991, 227:107-134.
[27]KORKUT E., ATLAR M. On the importance of the effect of turbulence in cavitation inception tests of marine propellers[C]. Proceedings of the Royal Society of London A. 2002, 458(2017): 29-48.
[28]PENG Xiao-xing, WANG Li and PAN Sen-sen. Air content effect on the vortex cavitation[J]. Journal of Hydrodynamics, Ser. A, 1989, 4(4): 60-68(in Chinese).
[29]ARNDT R., MARINE B. H. Nucleation and bubble dynamics in vortical flows[J]. Journal of Fluids Engineering, 2000, 122(3): 488-493.
[30]NAGAYA S., KIMOTO R. and NAGANUMA K. et al. Observation and scaling of tip vortex cavitation on elliptical hydrofoils[C]. The ASME-JSME-KSME Joint Fluids Engineering Conference. Hamamatsu,Japan, 2011, 225-230.
[31]PEREIRA F., SALVATORE F. and FELICE F.D. et al. Experimental and numerical investigation of the cavitation pattern on a marine propeller[C]. 24th Symposium on Naval Hydrodynamic. Fukuoka, Japan, 2002.
[32]BARK G., BERCHICHE N. and GREKULA M. Application of principles for observation and analysis of eroding cavitation-The EROCAV observation hand-book[M]. Chalmers, Sweden: Chalmers University of Technology, 2004.
[33]HOUT Y., TUKKER J. and GENT A. New developments on full scale cavitation observations[C]. 6th International Symposium on Cavitation. Wageningen, The Netherlands, 2006.
[34]HSIAO C. T., CHAHINE G. L. Scaling of tip vortex cavitation inception for a marine open propeller[C]. 27th Symposium on Naval hydrodynamics. Seoul, Korea,2008.
[35]PARK K., SEOL H. and CHOI W. et al. Numerical prediction of tip vortex cavitation behavior and noise considering nuclei size and distribution[J]. Applied Acoustics, 2009, 70(5): 674-680.
[36]HSIAO C. T., CHAHINE G. L. Scaling of tip vortex cavitation inception noise with a bubble dynamics modelaccounting for nuclei size distribution[J]. Journal of Fluids Engineering, 2005, 127(1): 55-65.
[37]ZHANG L., KHOO B. C. Dynamics of unsteady cavitating flow in compressible two-phase fluid[J]. Ocean Engineering, 2014, 87(9): 174-184.
[38]MOMPEAN G., GAVRILAKIS S. and MACHIELS L. et al. On predicting the turbulence-induced secondary flows using nonlinear k-εmodels[J]. Physics of Fluids, 1996, 8(7): 1856-1868.
[39]SCHMIDT S. J., SEZAL I. H. and SCHNERR G. H. et al. Shock waves as driving mechanism for cavitation erosion[C]. Proceedings of the 8th International Symposium on Experimental and Computational Aerothermodynamics of Internal Flows. Lyon,France, 2007.
[40]HSIAO C. T., CHAHINE G. L. Numerical study of cavitation inception due to vortex/vortex interaction in a ducted propulsor[C]. 25th Symposium on Naval Hydrodynamics. St. John's, Canada, 2004.
[41]ZHANG L., KHOO B. C. Computations of partial and super cavitating flows using implicit pressure-based algorithm(IPA)[J]. Computers and Fluids, 2013, 73(1):1-9.
[42]ZHANG Ling-xin, YIN Qin and SHAO Xue-ming. Theoretical and numerical studies on the bubble collapse in water[J]. Chinese Journal of Hydrodynamics,2012, 27(1): 127-132(in Chinese).
[43]CHOI C. L., CHAHINE G. L. A numerical study on the bubble noise and the tip vortex cavitaion inception[C]. 8th International Conference on Numerical Ship Hydrodynamic. Busan, Korea, 2003, 22-25.
[44]CHAHINE G. L. Nuclei effects on cavitation inception and noise[C]. 25th Symposium on Naval Hydrodynamics. St. John's, Canada, 2004.
[45]FRUMAN D. H., CERRUTTI P. and PICHON T. et al. Effect of hydrofoil platform on tip vortex roll-up and cavitation[C]. ASME Fluids Engineering Division. New Orleans, USA, 1993, 177: 113-124.
[46]YAKUBOV S., CANKURT B. and MAQUIL T. et al. Advanced Lagrangian approaches to cavitation modelling in marine applications[C]. 4th International Conference on Computational Methods in Marine Engineering. Amsterdam, The Netherlands, 2013, 217-234.
[47]YAKUBOV S., CANKURT B. and ABDEL-MAKSOUD M. et al. Hybrid MPI/OpenMP parallelization of an Euler-Lagrange approach to cavitation modeling[J]. Computers and Fluids, 2013, 80(1): 365-371.
[48]CHOI J. K., HSIAO C. T. and CHAHINE G. L. Tip vortex cavitation inception study using the surface averaged pressure (SAP) model combined with a bubble splitting model[C]. 25th Symposium on Naval Hydrodynamics. St. John's, Canada, 2004.
[49]CHAHINE Georges L. Numerical simulation of bubble flow interactions[J]. Journal of Hydrodynamics, 2009,21(3): 316-332.
[50]ZHANG Ling-xin, WEN Zhong-qing and SHAO Xueming. Investigation of bubble-bubble interaction effect during the collapse of multi-bubble system[J]. Chinese Journal of Theoretical and Applied Mechanics, 2013,45(6): 861-867(in Chinese).
(October 28, 2014, Revised March 3, 2015)
The propeller cavitation has a sustained attention since it was firstly discovered in the middle of the 19th century. Typically, the propeller cavitation can cause serious damages, such as noise, erosion and vibration. In recent decades, many studies revealed its fundamental mechanism as well as its engineering applications. In terms of different patterns, the propeller cavitation can be divided into four types, the bubble cavitation, the sheet cavitation, the cloud cavitation and the tip vortex cavitation (TVC). They have different patterns, as well as different occurrence mechanisms.
* Project supported by the State Key Program of National Natural Science of China (Grant No. 11332009), the National Natural Science Foundation of China (Grant No. 11272284).
Biography: ZHANG Ling-xin (1978-), Male, Ph. D.,Associate Professor
SHAO Xue-ming,
E-mail: mecsxm@zju.edu.cn
- 水动力学研究与进展 B辑的其它文章
- The analysis of flow characteristics in multi-channel heat meter based on fluid structure model*
- Theoretical analysis of slip flow on a rotating cone with viscous dissipation effects*
- Numerical and experimental study of Boussinesq wall horizontal turbulent jet of fresh water in a static homogeneous environment of salt water*
- Development of integrated catchment and water quality model for urban rivers*
- Analysis of temperature time series based on Hilbert-Huang Transform*
- A cavitation aggressiveness index within the Reynolds averaged Navier Stokes methodology for cavitating flows*

