Application of the edge of chaos in combinatorial optimization∗
Yanqing Tang(唐彦卿), Nayue Zhang(张娜月), Ping Zhu(朱萍),Minghu Fang(方明虎), and Guoguang He(何国光)
Department of Physics,Zhejiang University,Hangzhou 310027,China
Keywords: edge of chaos,chaotic neural networks,combinatorial optimization,travelling salesman problem
1. Introduction
Many problems in science,engineering and real life,such as traveling salesman problem(TSP),design of large-scale integrated circuits,[1]prediction of protein structure,[2]structural optimization of bimetallic nanoparticles,[3]and parameter estimation for chaotic systems[4]are related to the combinatorial optimization.Therefore,much attention has been attracted to designing a fast and efficient algorithm to obtain the globally optimal or near-optimal solutions to the combinatorial optimization problems. A variety of methods were proposed,such as cutting plane method,branch and bound method,and dynamic programming based on the Bellman’s principle of optimality.[1,5]However,the combinatorial optimization problems are usually NP-hard problems with time complexity in nondeterministic polynomial forms. With the increase of the scale of problems, the exact algorithms become powerless.Then, studies have been focused on the approximate algorithms or heuristic algorithms to seek near-optimal solutions of the problem with limited amount of computing time. Many algorithms were therefore proposed, such as stochastic simulated annealing (SSA) algorithm,[6–8]some algorithms based on biological phenomena,[3,8–13]and artificial neural network algorithms,[14–24]which have brought about some achievement in different scale problems.
In 1982, Hopfield neural networks was put forward and then was successfully applied to TSP.[14,15]Hopfield neural networks can quickly converge to a stable state, but it usually is not the globally optimal solution. The solution obtained is highly related to the initial value and the parameters. It is found that, even in the problems of 10 cities, the networks often converge to the local optimal solution,and the networks become powerless for larger scale problems.[14,15]On the other hand,the chaotic neural networks based on biological electrophysiological experiments have been proved to have ergodic property and can reach the globally optimal solution during cruising,but their chaotic motions make the networks unstable in the globally optimal solution. The solution therefore could not be obtained. Chenet al.proposed the transient chaotic neural networks(TCNN)algorithm based on chaotic neural networks (CNN) and simulated annealing algorithm, and applied their algorithm to TSP.[20]By controlling the attenuation of the feedback term,the network transits from chaotic state to stable state, thus reaches to the optimal solution. Compared with SSA algorithm, TCNN algorithm uses chaotic dynamics instead of Monte Carlo random to conduct annealing,which leads to less computing time and much higher probability of global optimum in TCNN algorithm.The globally optimal solution can be obtained in medium scale TSP problems with TCNN. However, Chenet al.found that 95%of the TSP solutions for 48 cities fell on the local optimal solutions, and the algorithm lacked the ability to jump out of those local optimal regions.
In order to improve TCNN algorithm,Wanget al. added noise into TCNN algorithm to enhance the randomness of search (stochastic chaotic neural network, SCNN) and the probabilities of the globally optimal solution for 10 cities and 21 cities were improved with the algorithm.[21]For larger scale problems (52 cities and 70 cities), the probabilities of valid solutions with SCNN algorithm were greater than that with TCNN algorithm. However, the probabilities of the globally optimal solutions for the two TSPs were not given in their work.[21]Besides, several other improved algorithms were proposed based on CNN,such as chaotic neural network with Gauss wavelet self-feedback,[22]frequency conversion sinusoidal chaotic neural network (FCSCNN),[23]and FCSCNN with hysteretic noise(HNFCSCNN).[24]Those algorithms enhanced the globally optimal probability in the TSPs of no more than 30 cities in certain degrees.However,no globally optimal solutions of larger scale problems were reported.[21–24]
Studies show that the algorithms based on chaotic neural networks have higher searching efficiency than many other algorithms.[20–24]At the initial stage of optimization,a chaotic neural network is in chaotic states. As time evolves, the chaotic neural network gradually degenerates into a stable state, optimization then is achieved. However, a shortcoming exists in the degradation of chaotic motion. At the moment that the chaotic neural network degenerates into a stable state,the system may be far away from the globally optimal solution, which leads to the degenerated neural network falling into a local optimal state.The globally optimal or near-optimal solutions thus cannot be obtained. In their work of controlling chaos in chaotic neural networks,Heet al. found that the controlled networks can converge on a stable mode related to the initial mode when the networks operate at the critical region between chaos and non-chaos,and believed that the edge of chaos (EC) plays a very important role in memory recall process.[25]In fact,many natural systems operate in the critical states between order and disorder,such as gene expression,morphogenesis, optimal cell growth, bacterial colonies and bird colonies.[26,27]In particular, a large number of theoretical models and experiments in neuroscience show that brain runs in the critical states between order and disorder,that is,on the edge of chaos.[28,29]Therefore,it has better abilities of information transmission, information processing, information storage and learning,and is relatively stable.[26,28]In addition,studies have revealed that artificial neural networks show better computing power when operating on the edge of chaos.[30]Recently, the critical characteristics of deep learning neural networks have attracted much attention. Computer scientists have found that in order to achieve faster learning and training and to reduce the loss of information in learning, machines can only run on the edge of chaos.[31]The possible reason is that the neural networks exhibit greater mutual information at the critical region and contains more metastable states, and the neurons show stronger correlation.[32]All the above studies illustrate that the neural networks have better ability on operation and information processing on the edge of chaos.Up to now, there is no report about the application of chaotic neural networks on the edge of chaos in the field of combinatorial optimization. TSP is one of the typical combinatorial optimization problems, and is often used as a touchstone of new algorithms. In this work,an algorithm for the combinatorial optimization problems is proposed based on chaotic neural networks on the edge of chaos,and the algorithm is applied to TSPs from 10 cities to 70 cities.
2. Model
In order to improve previous algorithms based on chaotic neural networks,we propose a method to solve TSP by using neural networks on the edge of chaos(ECNN).In the optimal process with the algorithm,firstly,the transient chaotic neural network is used. When the chaotic neural network degenerates to the stable neural network, the parameters of the neural network are modulated to make the neural network fall in a chaotic state close to the critical region between chaos and non-chaos again and start a new round of degradation from transient chaotic states to a stable state.Such switch ends after several rounds of degradation process according to the problem to be solved. In this way, the network runs in the critical states between chaos and non-chaos, that is, on the edge of chaos, where the network has the best searching ability.Thus, the ability for the network to obtain globally optimal or near-optimal solutions is enhanced. Aihaira chaotic neural network is established based on biological electrophysiological experiments.And its chaotic dynamics is similar to biological systems.[33]Therefore, Aihara chaotic neural network is selected to solve the combinatorial optimization problems.[20]Thei-th neuron of chaotic neural network on the edge of chaos can be described by the following equations:
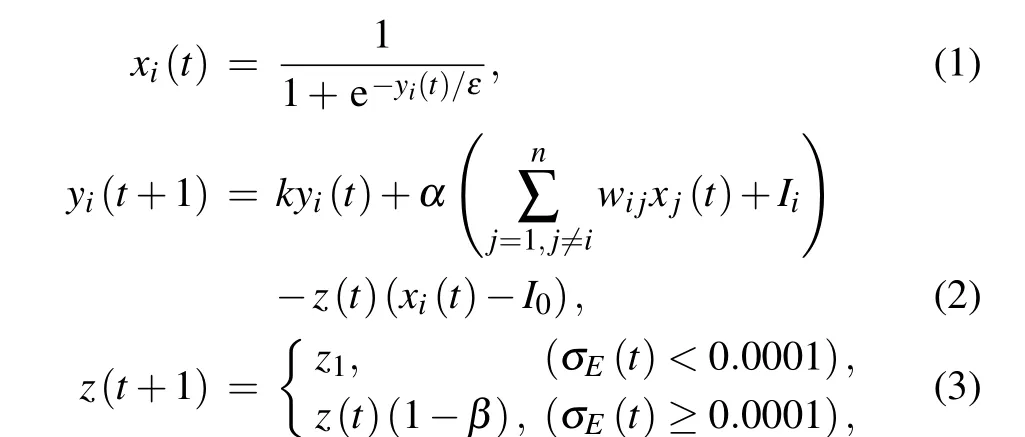
wherexiis the output of thei-th neuron,yiis the internal state of thei-th neuron,kis the damping factor of nerve membrane,αis the positive scaling parameter for inputs,εis the steepness parameter of the output function,Iiis the input bias of thei-th neuron,I0is a positive constant,andz(t)is the time-dependent self-feedback connecting weight or refractory strength.z1is the initial value of the self-feedback coefficient when the network becomes chaotic again.βis the damping factor ofz,which is chosen randomly for each annealing process to enhance the randomness of the network,that is,β=rand(βmin,βmax).β0is the damping factor of the first annealing process.wijis the connection weight from thei-th neuron to thej-th neuron,which satisfies
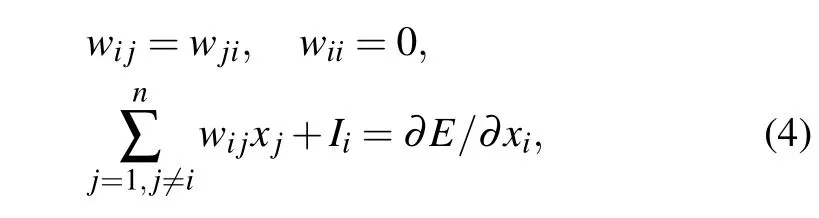
whereEis the energy function of a problem and the energy function of TSP will be defined in Eq.(7).σEis the variance of energy functions among the nearest 10 iterations. Large variance represents that the neural network is in the chaotic state, otherwise the network is in the stable state.σEis defined as follows:
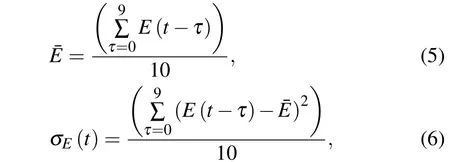
where ¯Eis the average energy function among the nearest 10 iterations.
Here, we use Eq. (3) to replace the feedback termz(t+1)=z(t)(1−β)in TCNN algorithm. In this way,when the network becomes stable, the sudden change of the feedback parameterzwill make the system chaotic again, so that the system has chance to escape from the local minimum region. The parameterz1is chosen close to the critical region that the network runs between chaotic state and stable state,namely on the edge of chaos, where the network has the best searching ability.
TSP is a typical combinational optimization problem. It seeks the shortest route for a traveling salesman to visit a certain number of cities and then to return to the starting point with the constrains of visiting each city once. For TSP withncities,a network withn×nlattice structure is constituted. Its neural output,xi j, represents to visit cityiin visiting orderj.The minimized tour length of TSP satisfying all constrains can be expressed by the energy function of the neural network as following:[20]
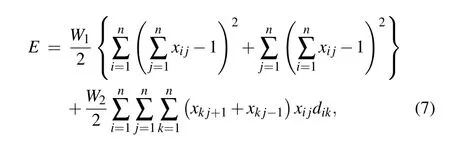
wherexi0=xin,xin+1=xi1,di jrepresents the distance between cityiand cityj,W1andW2represent the coupling parameters corresponding to the constraints and the cost function of the tour length, respectively. The first two terms of the equation indicate the constraints (each city can be accessed once only),and the last term represents the total length of the journey. When the energy function takes the minimum value, we get the shortest valid route satisfying the constrains.
Combining Eqs.(2),(4),and(7),one can find that based on ECNN,the TSP dynamics of a certain number of cities can be described by the following equation:
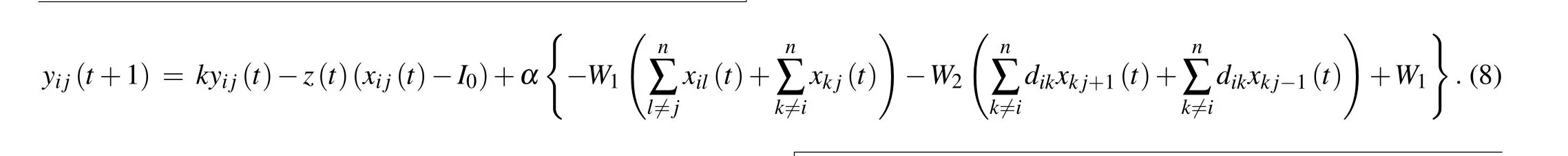
The initialyijare randomly generated with values between−1.0 and 1.0. Once the initial values are given, an optimal solution of the problem can be obtained through the evolution of the neural network.
3. Application of ECNN in TSP
We perform the simulations on the computer with the following specs: Dell PowerEdge R730 Server. Its CPU is E5-2650 V4@2.20 GHz and its memory size is 64G.The program is written in C language in a single threaded manner, that is,the output signals of the neurons are updated in turn in each iteration.
Firstly,ECNN algorithm is applied to TSP with 10 cities.The coordinate data of inter-city distance is from Ref. [15],and the globally optimal solution of the problem is given in Fig. 1. The parameters of the network are set ask= 0.9,α=0.015,z(0)=0.10,z1=0.035,I0=0.75,ε=1/250,W1=W2=1,β0=0.5,andβ=0.003.
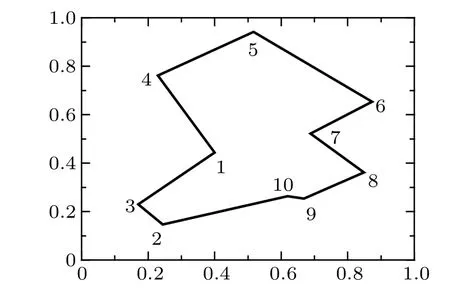
Fig. 1. The optimal tour of the 10-city TSP, each number in the tour represents one city.
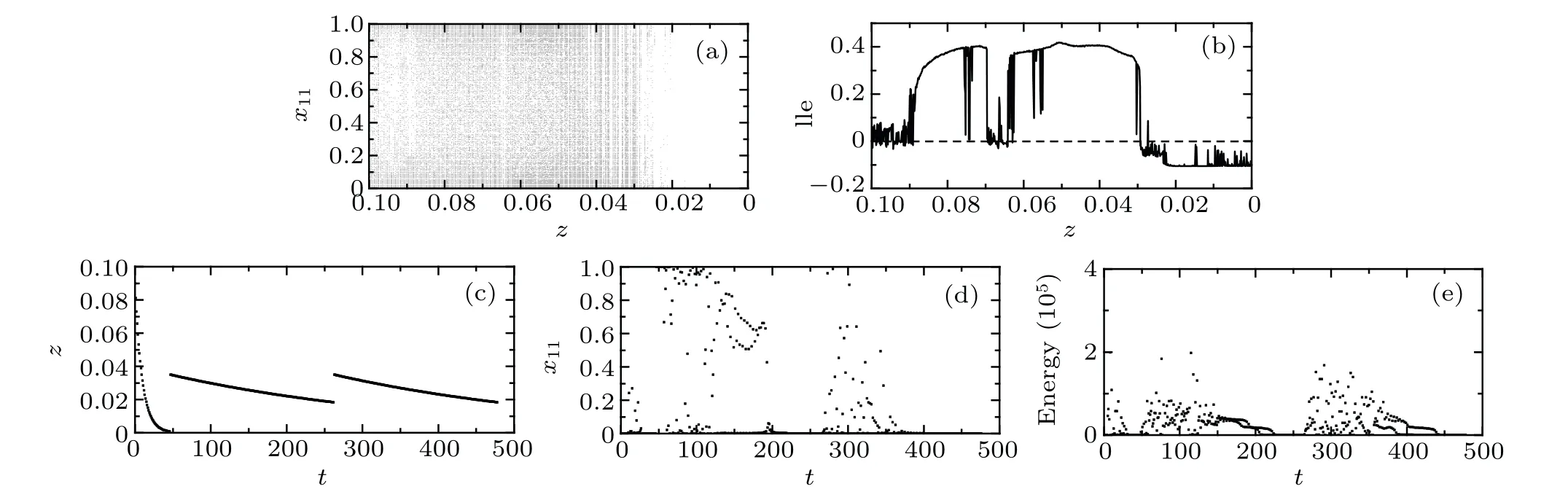
Fig.2. (a)The output distribution of one neuron(x11)in the chaotic neural network for 10-city TSP with the change of parameter z. (b)The largest Lyapunov exponent. (c)Evolution of the parameter z. (d)The output Evolution of one neuron(x11). (e)Evolution of the energy function E.
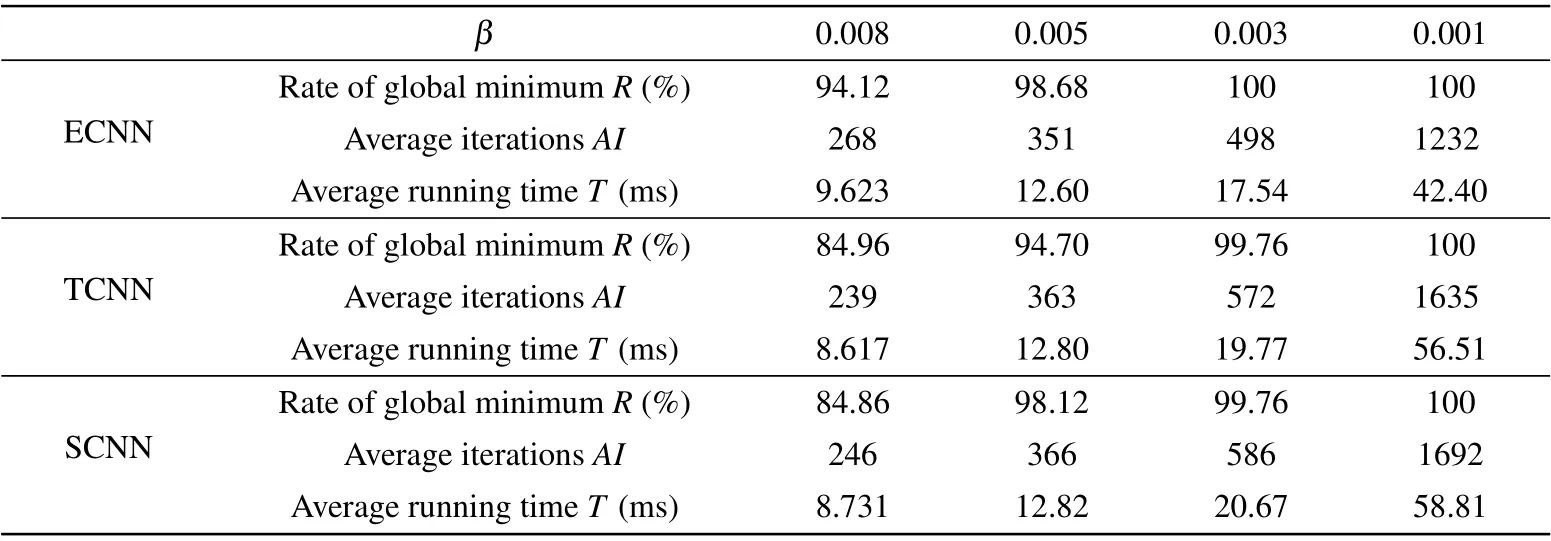
Table 1. Results with three algorithms for the 10-city TSP.
Since the behaviors of the neurons in the network are similar,we analyze the behavior dynamics of one neuron(x11)in the network as an example. Figure 2(a)shows output distribution of one neuron(x11)in the chaotic neural network for the 10-city TSP at different self-feedback parameterz.Figure 2(b)gives the largest Lyapunov exponent of the system calculated as the definition of Ref.[34]. Figures 2(a)and 2(b)are separated to two parts. In the right side with the self-feedback parameter less than 0.029,the largest Lyapunov exponent of the system is negative and the output signals of the neuron have certain discrete values, which means that the network is in a stable state. In the left side with the self-feedback parameter larger than 0.029,the largest Lyapunov exponent of the system is positive and the output signals of the neuron are randomized with the value range from 0 to 1 as seen in the dark region of Fig.2(a),which means that the network is in chaos. Based on Figs. 2(a) and 2(b), one can choose parameterzto make the system run on the edge of chaos. Figures 2(c)–2(e)show the evolution of parameterzin ECNN algorithm,the corresponding output evolution of one neuron (x11) and the corresponding evolution of the energy functionE,respectively. With the decrease of the feedback parameterz, the output of the neuron gradually converges to a stable point, the energy of the system gradually converges to a local minimum,and network becomes stable at the end of the first annealing process. For the TCNN algorithm and the SCNN algorithm,the simulation ends right now and an optimal solution is obtained. However,the system may be far away from the globally optimal solution and the degenerated neural network actually falls into a local minimum. For the ECNN algorithm, the self-feedback parameter is adjusted to be 0.035(z1), which is slightly larger than its critical value of 0.029. As a result,the output signals of the neuron and the energy of the system become random again, which means the system enters chaotic states near the critical region between chaos and non-chaos and a new round of annealing process begins. The system thus successfully escapes from the previously local minimum state. Then the system gradually converges to another stable state as the decrease ofz. Such switch ends after several rounds of degradation process according to the given ending rules. In this way, the network works in the critical region between chaos and nonchaos,that is,the network is on the edge of chaos.From above results, one can conclude that the chaotic neural network can be controlled to operate on the edge of chaos by modulating the self-feedback parameterz.
We simulate 5000 times for 10-city TSP with initial conditions ofyijgenerated randomly in the region [−1.0, 1.0].After three rounds of annealing process for each simulation,the optimal solution is obtained. It is found that the optimization efficiency is related to the value of the damping parameterβ. Whenβ ≤0.003, the rate of the globally optimal solution among all simulations can reach 100%. As a comparison,TCNN algorithm[20]and SCNN algorithm[21]are used for 10-city TSP. In SCNN simulations, the noise amplitudeA[n(0)]=0.002, and the damping factor of the noise isβ2=0.00005.[21]Other parameters are taken the same as those in ECNN algorithm of 10-city TSP.5000 simulations are made in both TCNN and SCNN algorithms,and the results are given in Table 1. It can be seen from Table 1 that compared with the other algorithms, ECNN algorithm shows the advantage in consuming time for optimization and the probability of the globally optimal solution.
Then, we solve the 21-city TSP, and the coordinate data of inter-city distance is obtained from Ref. [35]. The parameters are set asz1=0.035,I=0.5,W1=1.0,W2=1.0/980,β=0.0001,β=rand(0.00001,0.0003),and other parameters are the same as those we use in the 10-city TSP.12 rounds of annealing process are taken before each simulation ends and the globally optimal tour length we get is 2707. The globally optimal route is plotted in Fig.3.
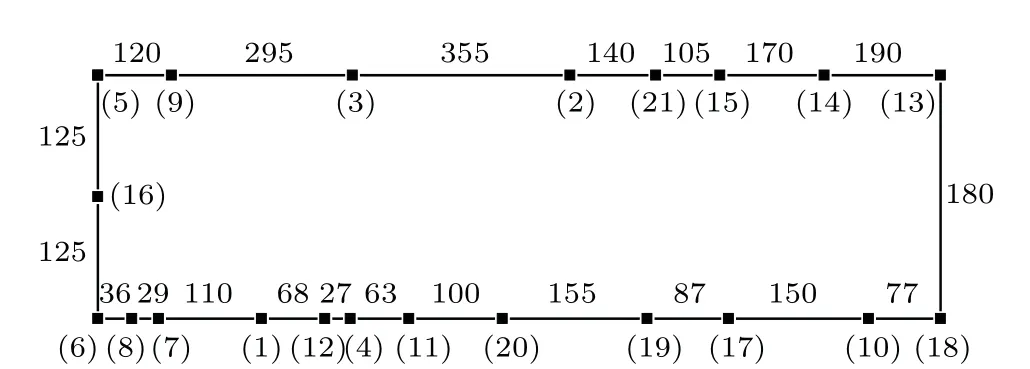
Fig.3. The optimal tour of the 21-city TSP with tour length 2707. Each number in brackets represents one city, whereas other numbers represent the distances between two cities.
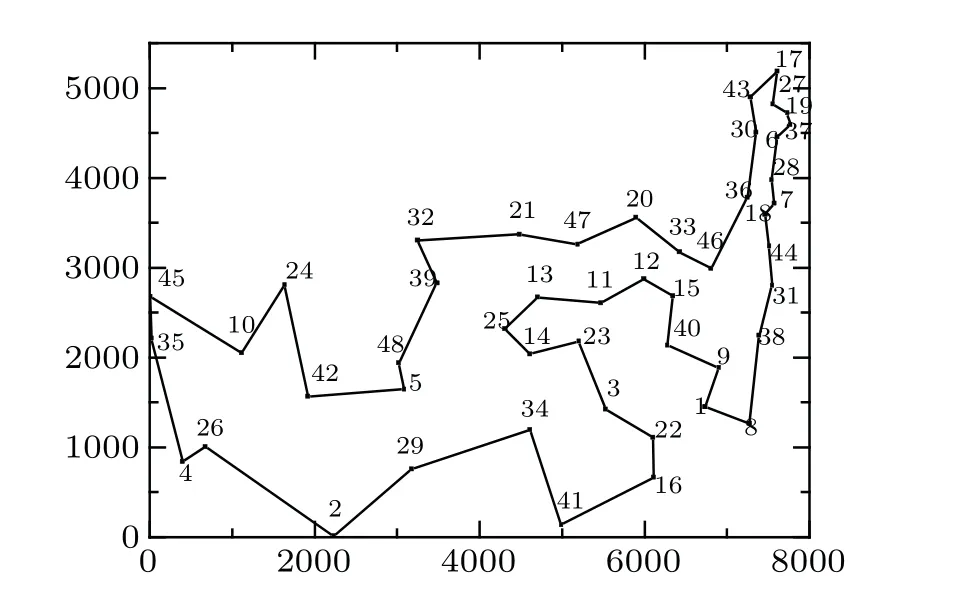
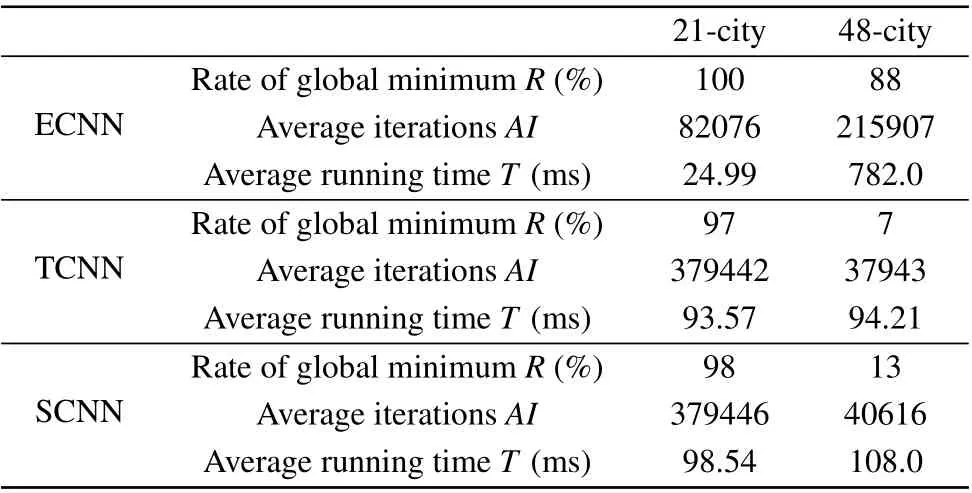
For 48-city TSP,the data of inter-city distance is also derived from Ref. [35]. In order to save computing time, we modify the ECNN algorithm. The feedback term in Eq. (2)is added only to the randomly chosenm×m(10 The parameters in the simulations of the 48-city TSP are set asz1= rand (0.027, 0.028),I= 0.75,W1= 1.0,W2=1.0/3160,β=0.00005, andβ=rand (0.000005, 0.00005).Other parameters are the same as those used in the 10-city TSP.In simulations,parameterz1is randomized between 0.027 and 0.028 for each annealing process, which makes the randomness of the network increase. Simulations end if more than 30 annealing had been done and there is no improvement in the nearest 20 consecutive annealing process. The globally optimal solution of the problem is derived in our simulations. The globally optimal tour length is 10628 and corresponding route is plotted in Fig.4. Fig. 4. The optimal tour of the 48-city TSP, each number in the tour represents one city. TCNN algorithm and SCNN algorithm are employed to 21-city and 48-city TSPs too. The results with 100 simulations for each case are summarized in Table 2. For SCNN algorithm, the noise amplitude is set asA[n(0)]=0.002 for 21-city TSP andA[n(0)]=0.02 for 48-city TSP and the noise damping factor is set asβ2=0.00005. The damping factors of the two algorithms are set asβ=0.000005 for 21-city TSP,andβ=0.00005 for 48-city TSP.Other parameters are taken the same as those in ECNN algorithm of 21-city and 48-city TSP. We find that smallerβcould not improve the calculating results for 48-city TSP.The reason is that with TCNN and SCNN algorithms,less iterations are taken for the 48-city TSP than for the 21-city TSP as seen in Table 2. Table 2. Results of three algorithms for the 21-and 48-city TSPs. As seen from Table 2, the probabilities of the global optimal solutions for both 21-city TSP and 48-city TSP with ECNN algorithm are higher than those with TCNN algorithm or SCNN algorithm. For 21-city TSP,the rate of the globally optimal solution with ECNN algorithm is only slightly higher that with TCNN and SCNN algorithm. However, much less computing time is demanded for ECNN algorithm to obtain the globally optimal solution of the problem. In particular,for 48-city TSP,the probability of the global optimal solutions with ECNN algorithm can reach 88%, while the probability with TCNN and SCNN algorithm is 7% and 13%, respectively. However, because of repeated switch between chaotic and non-chaotic states, the computing time in ECNN algorithm is the longest among the three algorithms. Considering the dominant superiority on the probability of the globally optimal solution,we believe that ECNN algorithm has a great improvement over TCNN and SCNN algorithms in solving 48-city TSP. At last, we apply our algorithm to the 70-city TSP, and the coordinate data of inter-city distances are from Ref. [35]too. The parameters of the algorithm are set asz1=0.028,I0=0.75,W1=1.0,W2=1.0/100,β=0.00005, andβ=rand(0.000005, 0.00005). Other parameters are the same as those used in the 10-city TSP. Simulations end based on the same rule as the 48-city TSP.The smallest tour length of 70-city TSP among 100 simulations is 679.However,the globally optimal tour length of the problem is 675.[35]There is a gap of 0.59%between our best solution and the globally optimal one.As a comparison, TCNN algorithm and SCNN algorithm are used for the 70-city TSP.In simulations, the damping factors of these algorithms are set as 0.000003,the noise amplitude of the SCNN algorithm is set asA[n(0)]=0.020,and the corresponding noise damping factor is set asβ2=0.00005. Other parameters are taken the same as those in ECNN algorithm of 48-city TSP. For each algorithm, we do 100 simulations.Both TCNN algorithm and SCNN algorithm fail in getting the globally optimal solution and the gaps of their best tour length from the globally optimal one are 0.59% and 1.03%, respectively. The summarized results for the 70-city TSP with three algorithms are listed in Table 3. Table 3. Results of three algorithms for the 70-city TSP. One can see from Table 3 that ECNN algorithm takes the least time to search the valid solutions among three algorithms. The probability of valid solutions with ECNN algorithm reaches 100%, while the probability with the other two algorithms is only at 54%. Besides, ECNN algorithm shows superiority in getting the best solution. The rate of the best solution is 21% with ECNN algorithm, while the rate is 1%and 5% with TCNN algorithm and SCNN algorithm, respectively. Considering the computing time and accuracy, we believe that ECNN algorithm demonstrates great advantages in solving TSP with a larger scale. For TSPs of 10 cities,21 cities,48 cities and 70 cities,our results prove that ECNN algorithm is much better in terms of optimization efficiency and accuracy than TCNN algorithm or SCNN algorithm,and provides an improvement in the solution of the combinatorial optimization problems. In order to clarify the superiority of our algorithm further, we firstly compare ECNN algorithm to several other recent works on TSP with improved algorithms based on CNN. The globally optimal probability for TSP of 30-city is 46% with the algorithm based on CNN with Gauss wavelet self-feedback,[22]30.5%with the FCSCNN algorithm,[23]and 49%with the HFCSCNN algorithm.[24]ECNN algorithm can drive the network away from local optimal states. Even in 48-city TSP, the globally optimal solution can be obtained at a probability of 88%with ECNN algorithm. This result is much better than those obtained by other algorithms based on CNN. Some algorithms based on biological phenomena were also proposed to solve the combinatorial optimization problems.[3,8–13]However, crossover, mutation and other extra operators for evolutionary are usually needed in these algorithms,[11,13,24]and the computing time thus are relatively longer. The local optimal solutions could not be avoided as well. In the work of Qiaoet al.,[24]the results of HNFCSCNN algorithm were compared with those of genetic algorithm(GA)[13]and particle swarm optimization(PSO)algorithm,[12]and it was found that the globally optimal solution for 30-city TSP were obtained by GA and PSO algorithm at a probability of 32.5%and 29%respectively. In the work of Denget al.,[11]a hybrid genetic algorithm was proposed and the best solution for 48-city TSP had a gap of 0.005%from the global optimal solution. With ECNN algorithm, the global optimal solution is obtained at a rate of 88%for 48-city TSP.Therefore,ECNN algorithm show advantage in the probability of the globally optimal solutions. In recent years, deep learning algorithms have attracted much attention and been introduced to the combinatorial optimization problems.[16–19]Globally optimal solutions can be reached in 20-city TSP[19]with deep learning algorithms,but for medium and large-scale TSP, it failed to obtain globally optimal solutions. For 50-city TSP and 100 city-TSP, the gap between the global optimal solution and the best valid solution obtained by deep learning algorithms is 0.12% and 0.87%, respectively.[19]Meanwhile, a large number of samples are required in deep learning algorithms. For example,in the work of Costaet al., about 10000 samples were used for each problem.[19]Samples are not easy to obtain as well,and it would require a lot of time to train samples. But samples are not required in the ECNN algorithm. Once the initial values are given, an optimal solution of the problem can be reached through the evolution of the neural network. Furthermore,a large probability of the globally optimal solutions can be obtained with ECNN algorithm for small and mediumsized problems. The algorithm based on the edge of chaos is therefore a good way to solve the combinatorial optimization problems. The number of iterations and the computing time is dependent on the scale of problems,the parameters of networks and the ending rule of a simulation as well. In general, more computing time is needed for larger scale problems. For TSP of 48 cities,we concentrate on finding the global optimal solutions of the problem at a high probability,and the parameters and ending rule are set to raise the traversal time in the chaotic region. The computing time with ECNN algorithm thus is longer than with TCNN algorithm or SCNN algorithm. However, for TSP of 70 cities, the global optimal solution could not be obtained with the ECNN algorithm since it is not easy to set suitable parameters. We therefore focus on searching for the best valid solutions of the problem. Traversal time in the chaotic region is shorten under the chosen parameters and ending rules.Thus,less computing time is needed with ECNN algorithm compared to the other two algorithms. It has been noticed that the parameters of networks are important to obtain optimal solutions in ECNN algorithm as in TCNN,[20]SCNN[21]and other algorithms based on chaotic neural networks.[22–24]For ECNN algorithm, solutions are sensitive to the initial value of the self-feedback coefficientz1,the damping factorβand the coupling parametersW1andW2. Parameterz1is chosen by a rule thatz1should be chosen to make the network near but not too close to the critical region, that is, on the edge of chaos. Larger values ofz1will cause the network to enter into the chaotic region deeper,thus reduces the optimization efficiency as well as the calculation accuracy. On the other hand,ifz1makes networks very close to the critical region between chaos and non-chaos,the traversal time in the chaotic region is too short to escape from a local minimum,thus reduces calculation accuracy. Studies have revealed that artificial neural networks show strong computing power when operating on the edge of chaos.[30]Thus by modulating the self-feedback parameterzto make the neural network operate on the edge of chaos, the optimization efficiency is improved and the probability of the globally optimal solution increase. The damping factorβand the coupling parametersW1andW2are selected according to the experience.However, it is not easy to find a set of appropriate parameters for TSPs with a large scale. The same problem exists in TCNN,[20]SCNN[21]and other algorithms based on chaotic neural networks.[22–24]Efforts have been made to conduct parameter selection. For example, the algorithm hybridization has been tested in optimization problems.[11,12]In the future,we will combine ECNN algorithm with other algorithms to improve parameter selection. Meanwhile, modulating important parameters by searching dynamics is another way we plan to try. In this work,an algorithm for the combinatorial optimization problems is proposed based on neural networks on the edge of chaos(ECNN),and is then applied to traveling salesman problems of 10 cities, 21 cities, 48 cities and 70 cities.The results show that for small scale TSPs of 10 cities and 21 cities,ECNN algorithm has higher probability of the globally optimal solutions and less time consumption than TCNN algorithm and SCNN algorithm. Since ECNN algorithm has more power to drive the networks away from local minimum,it shows stronger advantage in searching the globally optimal solution or near-optimal solution for larger scale TSP than TCNN algorithm and SCNN algorithm. In TSP with 48 cities,the probability of the globally optimal solution from ECNN algorithm can reach 88%,while the probabilities with TCNN and SCNN algorithm are only 6% and 13%, respectively. In 70-city TSP,ECNN algorithm provides much higher the probabilities of valid solutions and the best optimal solution,while spends less computing time than TCNN and SCNN algorithm.Moreover, ECNN algorithm is superior to other algorithms based on CNN,some algorithms based on biological phenomena and deep learning algorithms in searching for the optimal solutions of TSPs. To conclude,ECNN algorithm provides an effective way for solving the combinatorial optimization problems.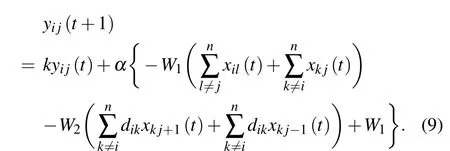

4. Discussion
5. Conclusion
- Chinese Physics B的其它文章
- Physical properties of relativistic electron beam during long-range propagation in space plasma environment∗
- Heterogeneous traffic flow modeling with drivers’timid and aggressive characteristics∗
- Optimized monogamy and polygamy inequalities for multipartite qubit entanglement∗
- CO2 emission control in new CM car-following model with feedback control of the optimal estimation of velocity difference under V2X environment∗
- Non-peripherally octaalkyl-substituted nickel phthalocyanines used as non-dopant hole transport materials in perovskite solar cells∗
- Dual mechanisms of Bcl-2 regulation in IP3-receptor-mediated Ca2+release: A computational study∗

