小净距隧道下穿薄煤层采空区地层开挖稳定性分析

刘书斌，周超月，方 勇

(西南交通大学交通隧道工程教育部重点实验室，成都 610031)

小净距隧道下穿薄煤层采空区地层开挖稳定性分析

刘书斌，周超月，方 勇

(西南交通大学交通隧道工程教育部重点实验室，成都 610031)

采空区地层离散性大，小净距隧道近接下穿不同倾角薄煤层采空区开挖将引起采空区内腔塌陷。建立小净距隧道近接下穿采空区地层开挖模型，对比分析采空区倾角为0°、15°、25°、40°时先行洞监测面洞周位移和初支内力。结果表明：后行洞初支闭合时，采空区倾角为15°时，拱顶下沉量最大；采空区倾角为40°时，仰拱隆起量和拱腰水平收敛量最大；随着采空区倾角增大，初期支护正(内)弯矩分布和轴力最大位置有向近接采空区侧移动的趋势，偏压越严重；应力集中逐渐由右拱脚向左拱脚移动。最大偏心距出现在拱脚处，采空区倾角为15°时，偏心距最小，初期支护稳定性最好；倾角为40°时，偏心距最大，不利于初期支护稳定。

小净距隧道；上覆采空区；倾角；初支内力；洞周位移

1 概述

采空区是煤矿工作面开采后形成的塌落空间。根据上覆围岩的破坏程度和变形特征，大致可分为采空区冒落带、裂隙带和弯曲带[1，2]。隧道下穿煤层采空区施工对围岩的扰动将打破现有的平衡状态，导致采空区内腔塌陷。尤其在冒落带，岩体松散而破碎，不仅降低了围岩承载力，还会引起隧道纵向、横向不均匀沉降，造成隧道衬砌结构的变形和开裂[3]。小净距隧道近接煤层采空区施工将不可避免地产生相互影响(当采空区与隧道间距较小，同时小净距隧道近接施工不可避免地产生相互影响)，同时后行洞开挖和煤层采空区将对先行洞初期支护稳定性造成叠加影响。

目前对于采空区地层隧道建设方面的研究已积累了一些经验[3，4]，对小净距隧道的研究则主要集中在双洞合理间距及中岩墙受力等方面[5，6]。方勇[3]等开展了公路隧道下穿双层采空区开挖过程模型试验，研究了双层采空区地层移动及隧道初期支护受力规律。张志沛[4]探讨了隧道工程在煤层采空区地段的治理方法，并在此基础上，提出了适合于隧道工程在煤层采空区地段治理的方法与对策。谢卓雄[5]运用小净距隧道三维开挖模型研究了两隧道掌子面距离的变化对小净距隧道结构的影响，得出了小净距隧道的空间相互影响效应。王树仁[7]等以师婆沟隧道为工程背景，运用 MIDAS/GTS 有限元程序构建 FLAC3D三维计算模型，对隧道初衬结构变形及受力特征等进行数值模拟分析。姚勇[8]等运用弹塑性数值模拟的方法，对Ⅲ、Ⅳ、Ⅴ级围岩小净距隧道中间夹岩的受力变形进行了研究，得出不同地质条件小净距隧道支护、开挖及岩墙加固的合理方法。黄明[9]对双向六车道连拱隧道邻近采煤空洞时的围岩稳定进行了数值计算，研究了Ⅵ级围岩条件下隧道附近采空区空洞处置及隧道围岩加固措施。钟祖良[10]等通过现场调研和数值模拟的方法，推导出能够考虑隧道左、右洞先后施工过程的隧道围岩压力计算理论。FU Yapeng[11]等通过弱化围岩参数将采空区等效为均质岩体，研究了上覆采空区倾角对隧道单洞的影响，得到倾角越小，施工风险越高。黄太武[12]通过对采空区桥梁群桩基础沉降进行数值模拟，分析采空区桩基在荷载作用下变形过程及特点，揭示不同工况下的基础变形规律。杨志浩[13]等通过控制变量法建立双层采空区隧道模型进行计算，考虑采空区高度及采空区之间间距的影响，对隧道开挖过程中围岩形变及位移、围岩应力及围岩塑性区的开展情况进行分析。

以上对于采空区的研究较多，同时对于小净距隧道施工后行洞的开挖对于先行洞的影响研究较多，但研究主要从采空区对于单洞隧道的影响和小净距隧道近接施工相互扰动的角度进行，很少研究采空区对于小净距隧道开挖的影响，尤其是采空区倾角和后行洞施工扰动对于先行洞稳定性的叠加影响。本文采用三维有限元方法，模拟采空区地层下修建双洞小净距隧道，通过对比不同倾角采空地层先行洞监测面的沉降、侧移及初期支护内力规律，分析采空区地层倾角对小净距隧道初期支护稳定性的影响。

2 计算建模

数值模拟采用有限差分计算软件FLAC3D进行，选取以Zienkiewicz-Pande为屈服准则的摩尔-库伦本构模型，模拟小净距隧道下穿不同倾角上覆采空区地层开挖过程，得到目标断面隧道洞周位移和衬砌内力，分析不同倾角采空区的存在对小净距隧道开挖初期支护稳定性的影响规律。

2.1 三维有限元模型

模型中采空区、基岩采用实体单元模拟，初期支护均采用壳(shell)单元模拟，模型尺寸为(宽×高)140 m ×130 m，纵向长16 m。上覆倾斜采空区与隧道间距为1 m，隧道跨径D为12.5 m，双洞间距0.5D，埋深70 m。隧道沿Y轴正方向开挖，分别模拟采空区倾角为0°(水平采空区)、15°(缓倾采空区)、25°(倾斜采空区)、40°(倾斜采空区)4种工况。隧道与采空区的空间位置(采空区倾角15°)如图1所示，三维有限元模型如图2所示。

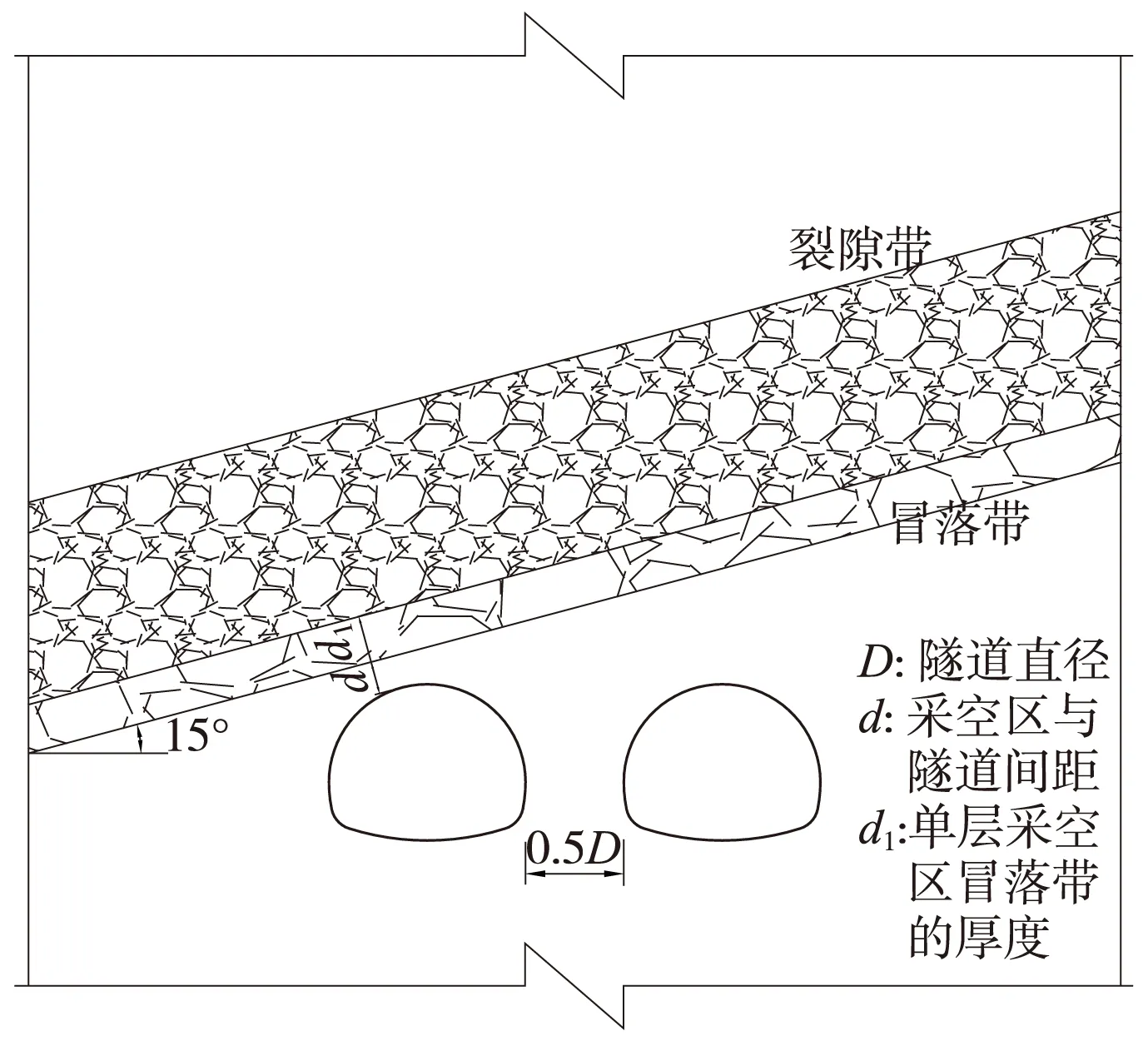
图1 采空区与隧道空间位置

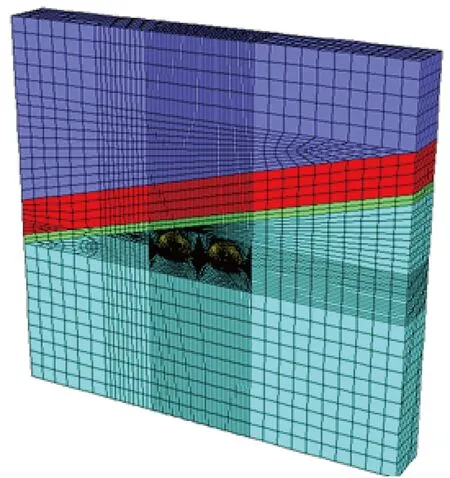
图2 三维有限元模型(采空区倾角15°)

为了消除边界效应的影响，模型中测试断面选在模型纵向中间断面(Y=8 m处)，分别在隧道断面的拱顶、仰拱、左右拱腰、拱肩和拱脚处布置监测点，分别监测拱顶和仰拱的竖向位移，拱肩、拱腰和拱脚的水平位移以及各个测点处的内力。测试断面监测点布置如图3所示。

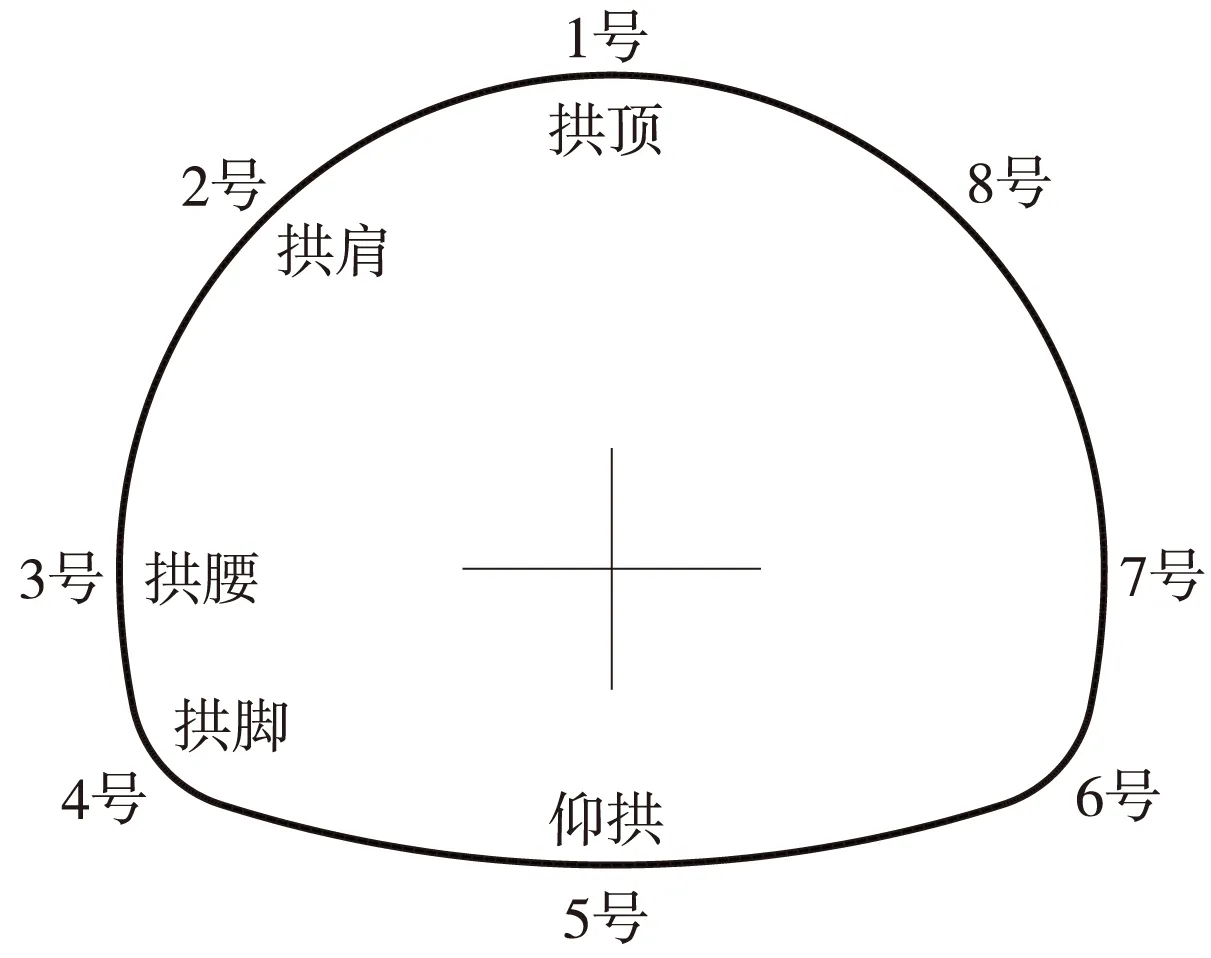
图3 测试断面监测点布置

2.2 模型参数的选取

通过弱化围岩参数来实现对采空区“三带”的模拟，参考《公路隧道设计规范》(JTG D70—2004)，文中采空区围岩级别取为Ⅴ级，基岩围岩级别选为Ⅳ级，采空区冒落带高度3 m，裂隙带高度12 m。采空区下部为基岩。采空区冒落带，裂隙带，弯曲带，基岩各参数见表1。

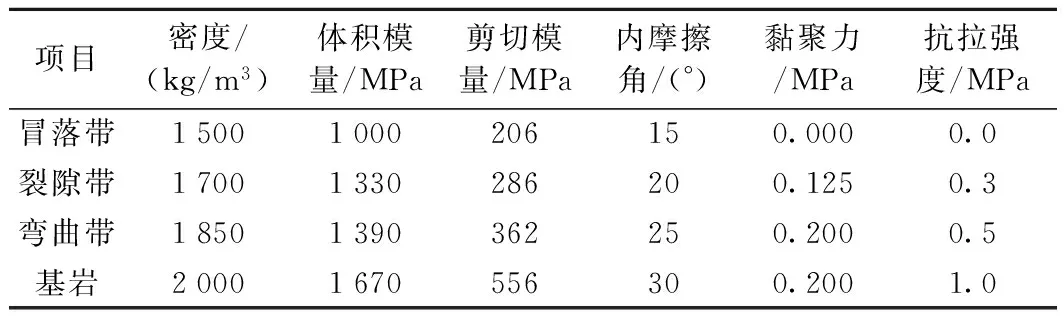
表1 围岩各参数取值

3 开挖模拟

隧道拟采用上下台阶法开挖，开挖同时完成支护，上台阶开挖7步后开始下台阶的开挖，并支护上下台阶。开挖顺序为先开挖左洞后开挖右洞，每步开挖进尺为2 m，上下台阶法的开挖步骤为：开挖上台阶(第1个进尺)→开挖上台阶(第2个进尺)， 支护(第1个进尺)→开挖上台阶(第3个进尺)，支护(第2个进尺)→依次循环开挖→开挖上台阶(第7个进尺)，开挖下台阶(第1个进尺)，支护上台阶(第6个进尺)→开挖上台阶(第8个进尺)，开挖下台阶(第1个进尺)，支护上台阶(第7个进尺)，支护下台阶(第1个进尺)→依次循环开挖。开挖并完成支护，左右洞共需29步。对于开挖的模拟，通过改变单元的材参实现。隧道内部土体及衬砌均为预设单元，分部开挖时，隧道核心土单元赋参为空单元，改变衬砌单元材参。开挖示意见图4。

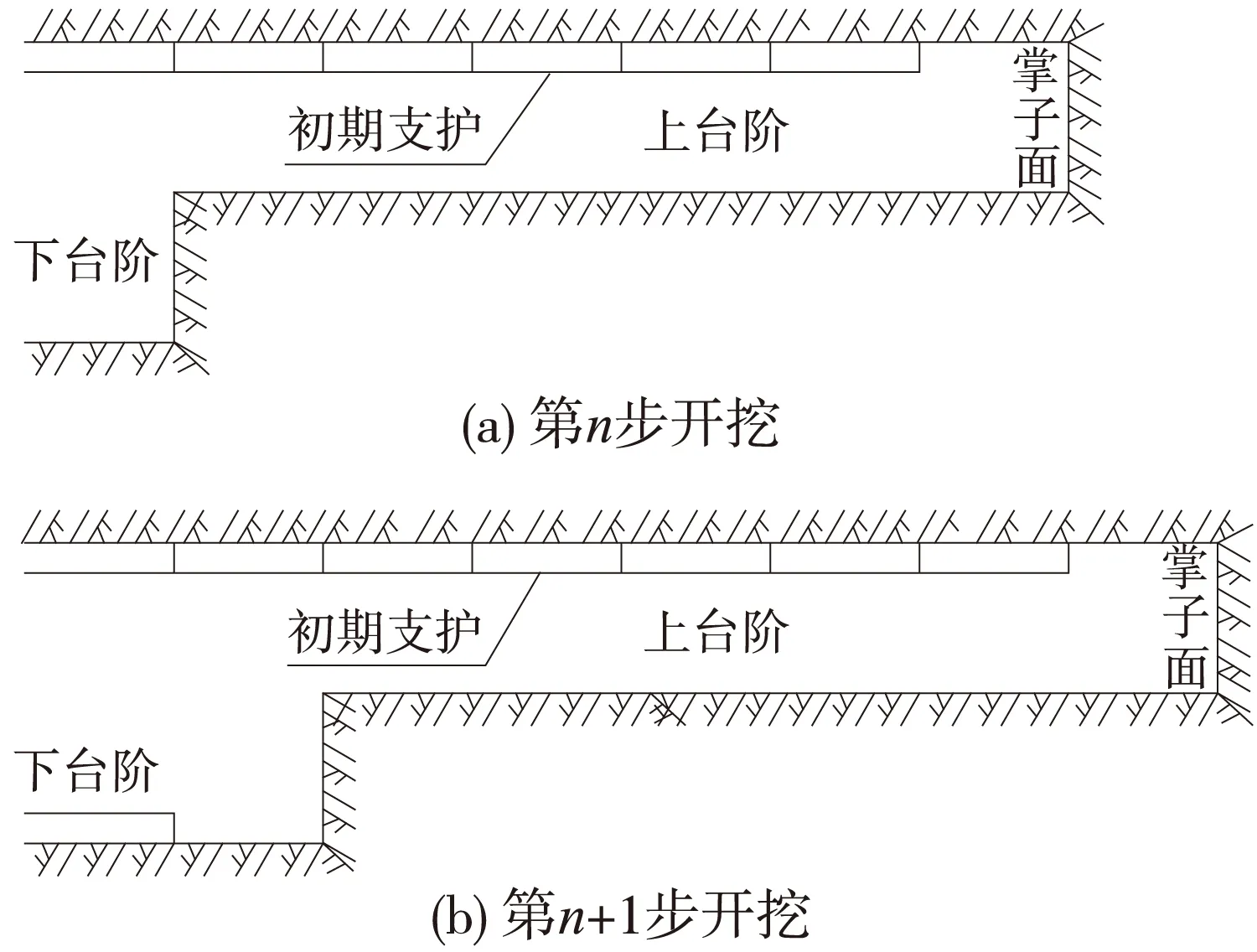
图4 开挖示意

4 计算结果分析

上覆采空区地层小净距隧道开挖，先行洞的稳定性必然受到后行洞开挖和采空区地层的叠加影响。通过分析监测面处各监测点的位移和内力，分析上覆采空区地层小净距隧道开挖过程中洞周位移及初支内力变化规律。

4.1 沉降分析

不同工况下目标断面拱顶沉降与开挖步的时程曲线如图5所示，拱顶下沉、仰拱隆起与倾角的关系如图6所示，仰拱竖向位移时程曲线如图7所示。

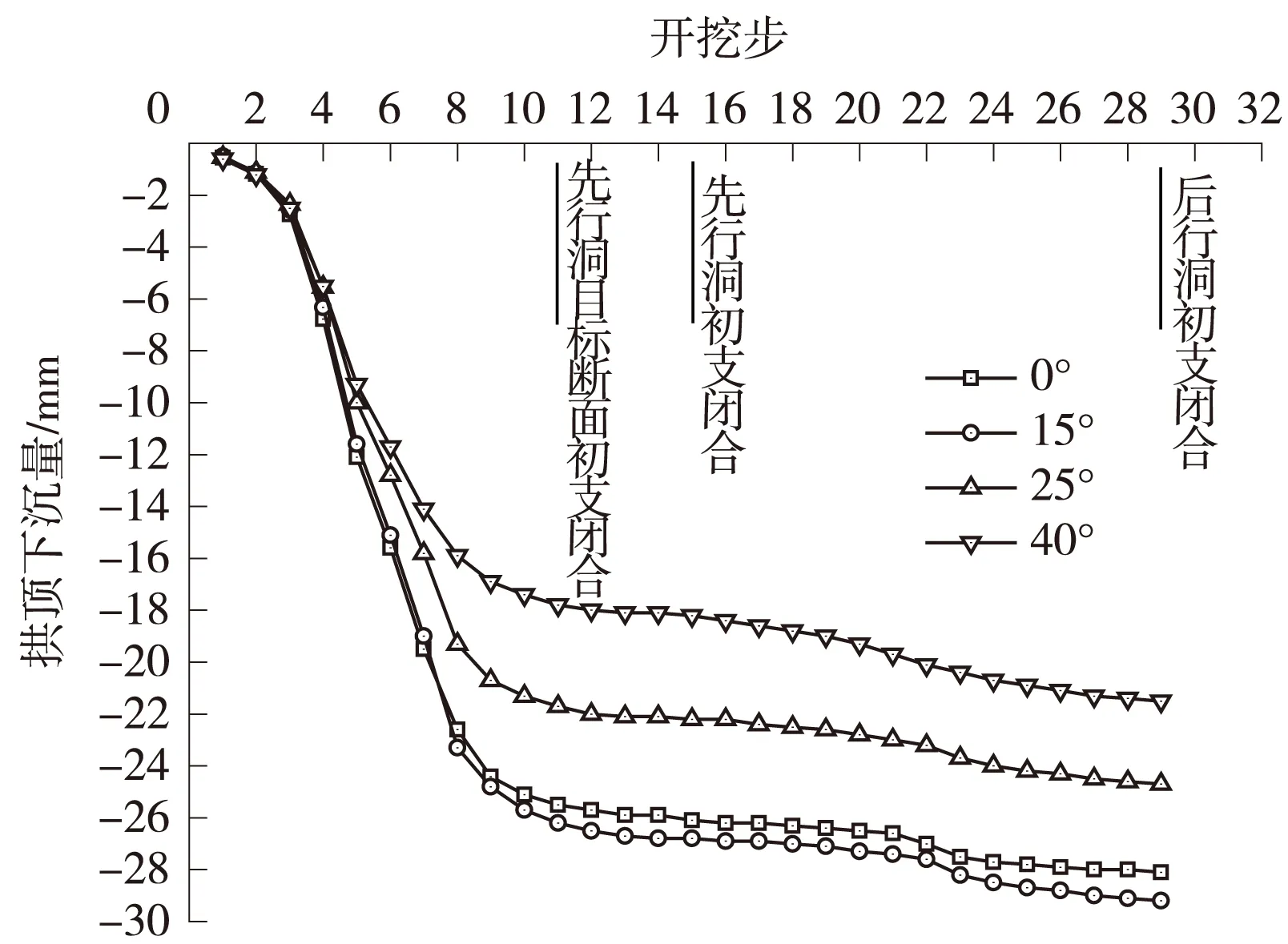
图5 拱顶下沉时程曲线

图6 拱顶下沉、仰拱隆起与倾角关系图

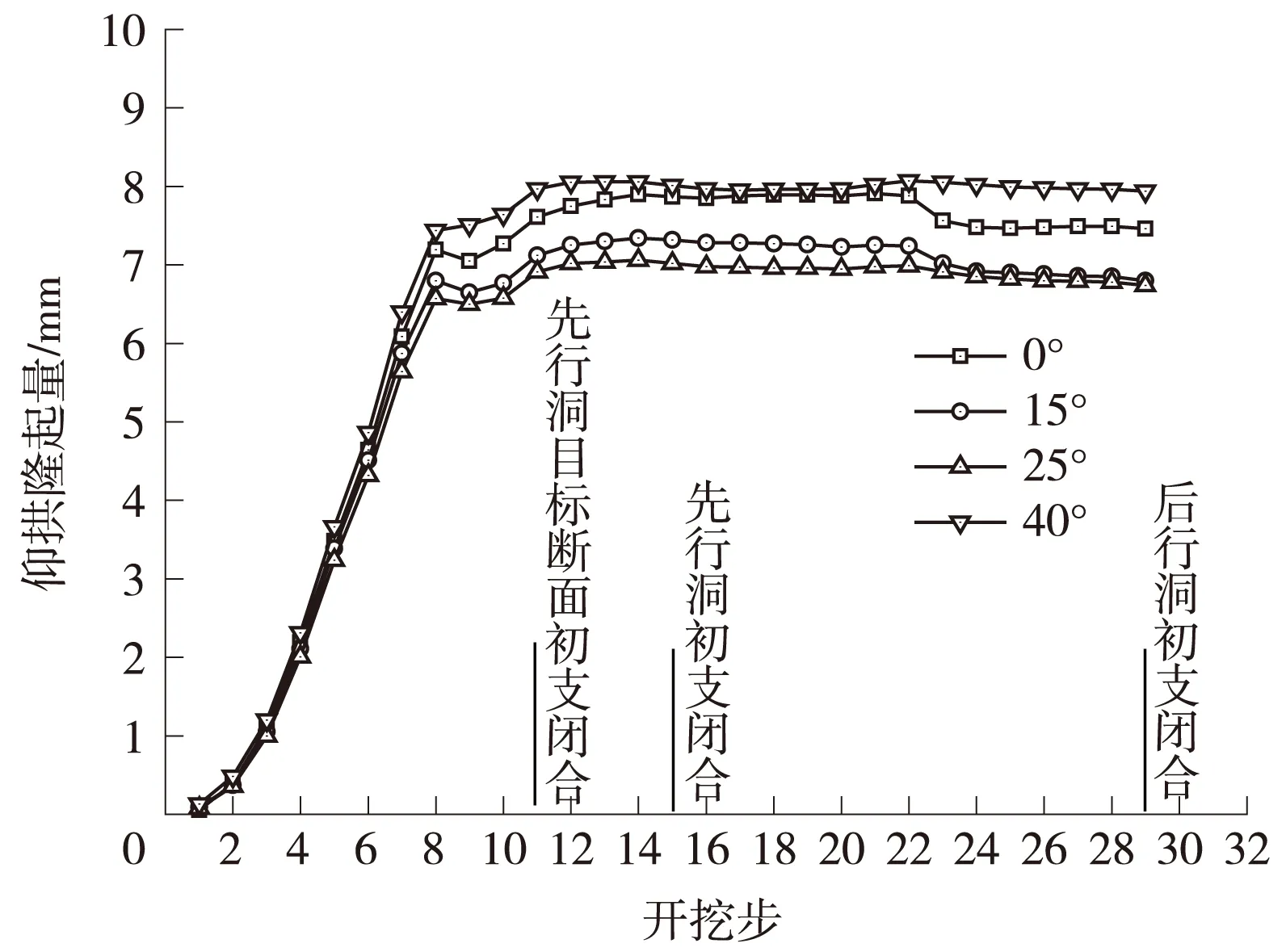
图7 仰拱竖向位移时程曲线

采空区小净距隧道不同倾角下先行洞拱顶下沉量随开挖步的变化趋势大致相同(图5)。从拱顶沉降量值分析：最大值出现在采空区倾角为15°时(29.2 mm)，比采空区倾角为0°时(28.1 mm)增大1.1 mm，增幅达3.91%；最小值出现在采空区倾角40°(21.5 mm)，约为倾角0°时的76.5%；倾角为25°时(24.7 mm)介于15°～40°。从拱顶沉降的变化趋势分析(图7)：小净距隧道先行洞在后行洞的影响下，采空区地层倾角从0°变为15°时拱顶下沉增加，倾角增大到25°时，拱顶下沉减小，变为40°时进一步变小。

通过图7可以看出，与拱顶沉降类似，不同倾角仰拱隆起量随开挖步的变化趋势大致相同。从仰拱隆起量值分析：后行洞初支闭合时，采空区倾角为40°时，小净距隧道先行洞在后行洞影响下仰拱隆起量最大(7.94 mm)，相比倾角0°时(7.46 mm)，增幅达6.43%；倾角为25°时仰拱隆起量最小(6.74 mm)，约为倾角0°时的90.35%。采空区倾角为15°时仰拱隆起量(6.8 mm)介于0°～25°。从变化趋势分析(图7)：小净距隧道先行洞在后行洞施工影响下，倾角从0°增大到15°时，仰拱隆起量减小，增大到25°时反而增大，倾角增大到40°时再次增大。

4.2 水平收敛分析

选取拱腰为水平收敛监测点，分别监测监测断面左右拱腰监测点X方向位移，先行洞监测点的侧移和水平收敛随开挖的时程曲线见图8、图9。

图8 拱腰侧移时程曲线

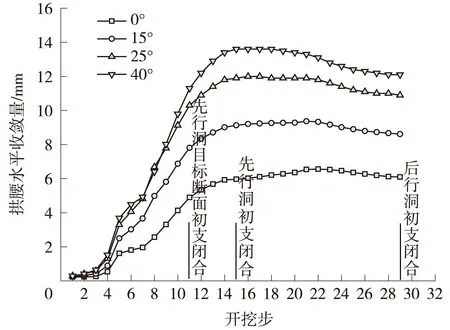
图9 监测断面拱腰水平收敛曲线

不同倾角采空区地层先行洞左、右拱腰监测点侧移量随开挖步的变化趋势相同。从拱腰侧移量值分析：后行洞初支闭合后，采空区倾角为40°时，左拱腰侧移量为11.6 mm，约为采空区倾角为0°时(2.7 mm)的4.30倍，倾角为15°和20°时分别为6.27 mm和9.25 mm，介于0°～40°之间。采空区倾角为40°时，先行洞右拱腰侧移量为0.483 mm，约为采空区倾角为0°时的14.21%。采空区倾角为15°和25°时分别为2.34 mm和1.64 mm，介于0°～40°。

从拱腰侧移变化趋势分析：小净距隧道先行洞在后行洞影响下，左、右拱腰侧移量在倾角为0°到40°的4种工况中分别呈现出依次增大、减小的趋势。同一角度时，左右拱腰侧移量大小不同，这是由于采空区地层离散性和荷载偏压导致。后行洞开挖过程对右拱腰侧移量影响较大，对左拱腰侧移量影响较小。倾角为40°时，后行洞开挖造成右拱腰侧移量达到最大值2.157 mm，倾角为0°时，为最小值0.29 mm。倾角为15°和20°时分别介于0°～40°，分别为0.99 mm和1.63 mm。由此，采空区倾角为40°时，应加固中岩墙。

隧道水平收敛量为左右拱腰侧移量之和。由图9看出，不同倾角采空区地层下先行洞水平收敛量随开挖步的变化趋势大致相同，均在先行洞初支闭合时出现最大值。至后行洞初支闭合，倾角为40°时，拱腰水平收敛为4种工况中的最大值(12.1 mm)，相比倾角为0°时(6.1 mm)增幅达1倍。倾角为15°和25°时介于0°和40°，分别为8.61 mm和10.9 mm。从变化趋势角度分析，由图10看出，小净距隧道先行洞在后行洞施工扰动影响下，采空区倾角从0°增大到40°的4种工况中，拱腰水平收敛值依次增大，倾角为40°时达到最大值1.5 mm。究其原因，采空区地层倾角造成地层偏压荷载偏压，在后行洞施工扰动的影响下，影响左右拱腰处侧移值和水平收敛值。对小净距隧道下穿倾斜采空区的工况，应该及时封闭初期支护，倾角较大时并加固中岩墙。

图10 拱腰水平位移与倾角关系

4.3 内力分析

隧道荷载主要来自于上覆围岩的松动塌陷，下覆围岩主要提供基底抗力。采空区为松散堆积体，重度与围岩存在差异，隧道开挖引起上部采空区的垮塌，同时倾斜采空区的存在必定造成上覆荷载的偏压，影响对初期支护内力分布。监测面最终弯矩和轴力如图11、图12所示。

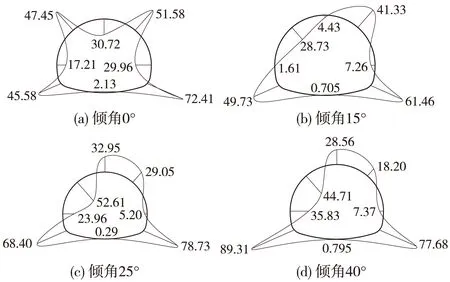
图11 不同工况监测面弯矩(单位：kN·m)

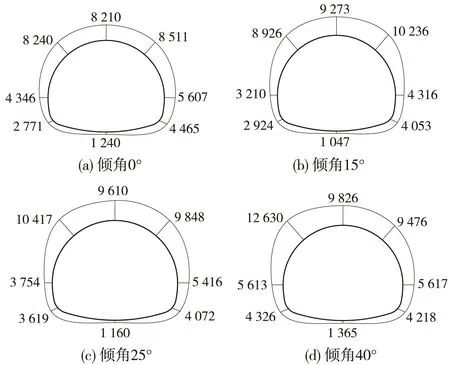
图12 不同工况监测面轴力(单位：kN)

至后行洞初支闭合，小净距隧道先行洞在后行洞施工扰动下，采空区倾角不同，弯矩量值、分布形态及最大值出现位置均不相同。从弯矩图量值看，采空区倾角为0°时，最大正(内)、负(外)弯矩出现位置分别为拱顶(30.72 kN·m)和右拱脚处(72.41 kN·m)。倾角为15°时，最大正(内)、负(外)弯矩出现位置分别为左拱肩(28.73 kN·m)和右拱脚(61.46 kN·m)。倾角为25°和40°度时，最大正(内)弯矩出现位置均为左拱肩处，量值分别为52.61 kN·m和44.71 kN·m；最大负(外)弯矩出现位置分别为右拱脚(78.73 kN·m)和左拱脚处(89.31 kN·m)。采空区不同倾角下，弯矩绝对值最大值均出现在拱脚处，拱脚处出现应力集中。

从分布形态来看，采空区水平时，弯矩基本对称分布；采空区倾斜时，弯矩图分布不对称，验证了采空区造成地层荷载偏压。采空区倾角增加，拱顶正弯矩区先向左拱肩处移动并扩大，然后向左拱腰处移动并有减小趋势，右拱肩处负弯矩区向拱顶方向移动，量值先扩大然后减小，左拱脚处弯矩持续增大；同时，应力集中部位由右拱脚处向左拱脚处转移的趋势。倾角为0°时，左拱肩处弯矩为-47.45 kN·m，拱顶弯矩为30.72 kN·m，左拱脚处弯矩为-45.58 kN·m；采空区倾角为15°时，拱肩弯矩由负弯矩变成正弯矩28.73 kN·m，拱顶正弯矩也明显减小为4.43 kN·m，左拱脚处弯矩增大为49.79 kN·m。倾角为25°时，左拱肩处正弯矩进一步增加到52.61 kN·m，左拱腰处弯矩也明显增大为23.96 kN·m，拱顶处弯矩由正弯矩变成负弯矩为-32.95 kN·m，左拱脚处弯矩增大到68.40 kN·m。倾角为40°时，左拱肩处弯矩减小到44.71 kN·m，左拱腰处弯矩持续增加到35.83 kN·m；拱顶负弯矩减小到28.56 kN·m；左拱脚处弯矩增大到89.31 kN·m。

从初期支护轴力图分布形态来看，轴力图分布呈现出拱部较大，底部较小的状态。拱顶、拱肩处弯矩值相对较大，且采空区倾角增大，拱顶及左拱肩处轴力有增大的趋势，即初期支护距离采空区较近部位轴力增大。采空区倾角为0°时，拱顶及左拱肩轴力值分别为8 210 kN和8 240 kN，采空区倾角为15°时，拱顶和左拱肩处轴力值为9 273 kN和8 926 kN，有明显的增大；采空区倾角为25°和40°时，继续增大；倾角为40°时拱顶和左拱肩处轴力达到最大值分别为9 826 kN和12 630 kN。这与采空区倾角的不同造成地形荷载的偏压有关，距离采空区较近部位承受左右侧较大土压力，而产生较大的轴力。拱腰、拱脚及仰拱位置轴力相对较小。

对于一定范围内隧道初期支护的稳定性取决于所承受的轴力和弯矩，轴力有利于结构的稳定。偏心距(弯矩和轴力之比)是评价初期支护稳定性的重要指标。采空区不同倾角下初期支护各个部位的最大偏心距如表2所示。从表2可以看出，4种工况下，正(内)弯矩引起的偏心距普遍较小。应力集中在拱脚处，拱脚处的偏心距较大。倾角40°时，左拱脚处偏心距出现最大值20.77 mm，最不利于结构稳定；最小值为倾角15°时(15.16 mm)，初支稳定性最好。倾角为0°和25°时，最大偏心距出现在右拱脚处，分别为16.22 mm和19.33 mm，稳定性介于15°和20°之间。

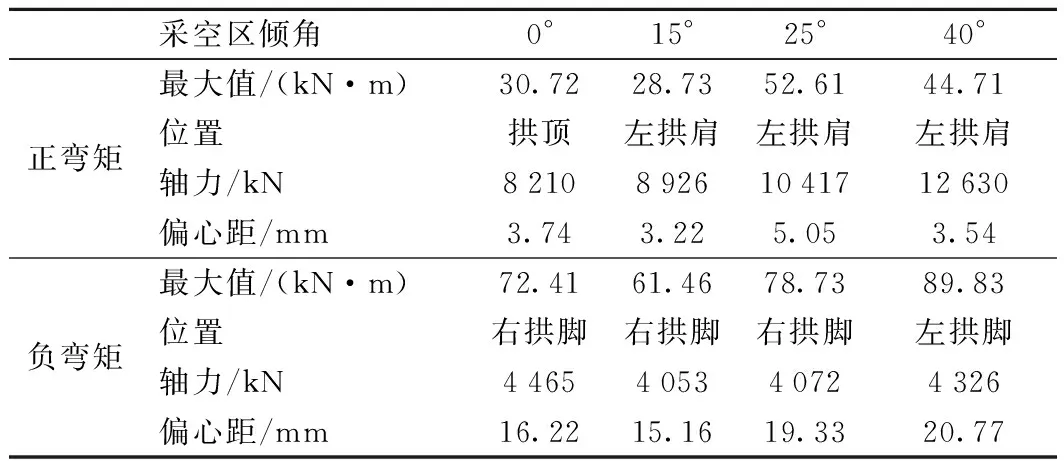
表2 监测面初支内力汇总

5 结论及建议

缓倾斜和倾斜采空区的存在造成地层的偏压。小净距隧道下穿缓倾斜和倾斜采空区地层开挖会破坏地应力平衡状态，造成采空区内腔塌落。通过开展小净距隧道开挖数值模拟，分析了先行洞中间断面的洞周位移和初期支护内力，得到了采空区地层和后行洞开挖对先行洞初支稳定性的叠加影响规律：

(1)小净距隧道先行洞在后行洞施工扰动下，后行洞初支闭合时，采空区倾角约为15°时，拱顶下沉量最大，故遇到类似工况应缩短上台阶初期支护时间，并增大初期支护刚度以保证稳定性。采空区倾角为40°时，仰拱隆起量最大，应及时闭合初支断面；拱腰水平收敛最大，同时后行洞开挖对于先行洞右拱腰侧移影响最大，应该及时封闭初期支护，增大初期支护刚度并加固中岩墙。

(2)小净距隧道先行洞在后行洞施工扰动的影响下，采空区由水平变倾斜并且倾角增大过程中，后行洞初支闭合后先行洞初期支护正(内)弯矩分布区有向左侧(靠近采空区侧)移动的趋势，从拱顶到左拱肩并逐渐下移。拱脚处发生应力集中，并且应力集中部位从右拱脚向左拱脚移动的趋势。轴力最大位置也由拱顶向左拱肩移动并继续增大。

(3)至后行洞初期支护闭合，偏心距最大位置发生在拱脚处，采空区倾角为15°时，偏心距最小，初期支护稳定性最好。倾角为40°时，偏心距最大，不利于初期支护稳定。

[1] 童立元，刘松玉，邱钰，等.高速公路下伏采空区问题国内外研究现状及进展[J].岩石力学与工程学报，2004，23(7):1198-1202．

[2] 段敬民，钱永久，曾宪桃.塌陷区地表房屋抗采动结构体系及其加固[J].工程力学，2007，24(S1):94-97.

[3] 方勇，符亚鹏，周超月，等.公路隧道下穿双层采空区开挖过程模型试验[J].岩石力学与工程学报，2014(11):2247-2257．

[4] 张志沛，覃羡安，刘旭.隧道在煤层采空区的治理方法[J].公路，2005(8)：176-179．

[5] 谢卓雄.小净距隧道近接施工围岩稳定性及结构力学行为特征研究[D].成都：西南交通大学，2005．

[6] 龚建伍，雷学文.大断面小净距隧道围岩稳定性数值分析[J].岩土力学，2010(S2):412-417．

[7] 王树仁，张海清，慎乃齐，等.下伏采空区桥隧工程变形及受力响应特征分析[J].岩石力学与工程学报，2009，28(6):1144-1151．

[8] 姚勇，何川，谢卓雄.双线小净距隧道中岩墙力学特征及加固措施研究[J].岩土力学，2007，28(9):1883-1888．

[9] 黄明，张旭东，刘华荣.采空区大跨连拱隧道围岩稳定分析及其加固[J].广西大学学报：自然科学版，2012，37(1):128-133.

[10]钟祖良，涂义亮，刘新荣，等.浅埋双侧偏压小净距隧道衬砌荷载及其参数敏感性分析[J].土木工程学报，2013，46(1):119-125．

[11]Fu Yapeng， Fang Yong， Cui Ge， Yang Bin. Influence of overlying goaf dip angle on stability of highway tunnel during excavation[C]. IACGE2013， Chengdu， ASCE， 2013(232):507-514.

[12]黄太武.高速铁路采空区桥基沉降变形数值模拟分析[J]. 铁道标准设计，2014(3):71-76．

[13]杨志浩，方勇，周超月，等.双层采空区隧道开挖围岩稳定性数值模拟[J].铁道标准设计，2015(3):97-100.

Analysis of Excavation Stability of Twin Tunnels Under-crossing Thin Mined-out Coal Area

LIU Shu-bin， ZHOU Chao-yue， FANG Yong

(MOE Key Laboratory of Transportation Tunnel Engineering， Southwest Jiaotong University， Chendu 610031， China)

Mined-out area is of high discreteness. The construction of twin tunnels undercrossing thin mined-out coal area with different dip angles may lead to inner cavity collapse， causing bias load. A model of twin tunnels excavated undercrossing mined-out coal area is established to analyze the hole perimeter displacement and the primary support internal force of the monitoring section of the tunnel first excavated when the dip angle of the mined-out coal area is 0°，15°，25°and 40°. The results show that after the primary support of the second tunnel is closed， the vault settlement of the tunnel first excavated is the biggest when the dip angle is about 15°; when the dip angle of the mined-out coal area is 40°， the invert displacement and the arc spring level convergence is the biggest; as the dip angle of the mined-out area increases， the positive bending moment and the maximum axial force position of the primary support tend to move to the side close to the mined-out area， and the load bias is more serious; the stress concentration position tends to move from right arch spring to left arch spring. The maximum eccentricity position is at the arch spring. The minimum eccentricity appears when the dip angle of mined-out coal area is 15°and the stability of primary support is at its best. While， the maximum eccentricity shows up when the dip angle of mined-out coal area is 40°， and the stability of primary support is the weakest．

Twin tunnels; Overlap mined-out coal area; Dip angle; Primary support internal force; Hole perimeter displacement

2015-02-01；

2015-03-02

刘书斌(1991—)，男，硕士研究生，E-mail:52175856@qq.com。

方 勇(1981—)，男，副教授，博士，主要从事隧道及地下工程方面的研究，E-mail：fy980220@swjtu.cn。

1004-2954(2015)10-0128-06

U455.43

A

10.13238/j.issn.1004-2954.2015.10.029