1 520 mm宽轨高速铁路平面曲线设计参数研究

王 诗

(中铁二院工程集团有限责任公司，成都 610031)

1 520 mm宽轨高速铁路平面曲线设计参数研究

王 诗

(中铁二院工程集团有限责任公司，成都 610031)

研究旨在为我国高速铁路在1 520 mm宽轨地区的应用提供平面曲线参数的计算方法和设计选用的参考。运用我国高速铁路设计规范中的计算方法和判定条件，计算1 520 mm宽轨高速铁路平面曲线设计参数，分析不同平面曲线半径和设计超高对列车行驶安全和旅客舒适度的影响，得出不同的速度目标值对应的平面曲线参数结果，包括曲线半径合理取值范围、最小曲线半径取值和缓和曲线长度值。研究结论：(1)1 520 mm宽轨高速铁路最小曲线半径主要受到设计速度和速度匹配的影响，设计速度越高，速差越大，最小曲线半径值越大；(2)在同等条件下，1 520 mm宽轨的最小曲线半径取值大于标准轨的最小曲线半径取值；(3)缓和曲线长度值主要受设计超高和设计速度控制，与轨距基本无关。

高速铁路；1 520 mm宽轨；平面曲线设计参数

1 概述

随着我国高速铁路“走出去”战略的积极推进，“中国高铁”作为一项国际品牌已相继进入亚、非、欧、美等市场。特别是近年来国家“一路一带”战略的提出和实施，为我国高速铁路的发展和推广提供了空前的契机。目前，我国同“丝绸之路经济带”沿线国家的高铁合作正紧锣密鼓地研究和筹备中。其中俄罗斯、蒙古、哈萨克斯坦、塔吉克斯坦等“丝路国家”采用轨距为1 520 mm的宽轨铁路，与我国的1 435 mm标准轨距铁路有所不同。在上述国家开展高铁合作项目，将会面临由铁路轨距不同带来的诸多问题。然而，国内对宽轨铁路的研究甚少，有关宽轨高速铁路的文献更为稀少。因此在当前中国高速铁路“走出去”的时代背景下，研究1 520 mm宽轨高速铁路的平面曲线设计参数，具有十分重要的现实意义。

从中国高速铁路设计规范的标准体系出发，通过计算平面曲线半径、超高、缓和曲线长度等参数，研究1 520 mm宽轨高速铁路平面曲线设计参数取值，为我国在1 520 mm宽轨铁路国家和地区开展高速铁路项目合作提供参考。由于不同项目采用的机车车辆或者动车组的生产国以及型号都有所不同，加之缺乏相关技术参数，故本文不考虑宽轨车辆的相关技术参数情况，仅在此基础上展开研究。

2 研究理论和计算公式

本文主要基于我国高速铁路设计规范的标准体系，研究1 520 mm宽轨铁路在高速情况下的平面曲线设计参数取值情况，主要运用了以下理论和计算公式。

2.1 外轨超高理论

机车车辆在曲线上行驶时，由于惯性离心力作用，被推向外股钢轨，加大了外股钢轨的压力，使旅客产生不适，货物移动。因此需要把曲线外轨适当抬高，使机车车辆的自身重力产生一个向心水平分力，以抵消惯性离心力，达到内外两股钢轨受力均匀和磨耗均匀等，满足旅客舒适度要求，提高铁路的稳定性和安全性[1]。由此产生了外轨超高，外轨超高是指曲线外轨顶面与内轨顶面水平高度之差。

上述理论即为经典外轨超高理论，它是铁路曲线、超高和缓长设置的基本理论，得到国际广泛认可和采用。

2.2 外轨超高计算公式

当抬高外轨使车体倾斜时，轨道对车辆的反力和车体重力的合力形成向心力，如图1所示。

图1 外轨超高计算图式

图中P——车体重力；

Q——轨道反力；

Fn——向心力；

S1——两轨头中心线距离；

h——所需的外轨超高度。

由图1可知：△ABC～△EDO

OE/OD=AC/CB

由于超高很小，从工程使用的角度，可取CB≈AB=S1

则

(1)

车体作曲线运动产生的离心力为

(2)

式中g——重力加速度，N/s2；

v——行车速度；单位取为m/s时用v，取为km/h时是V;

R——曲线半径。

为使外轨超高度与行车速度相适应，保证内外两股钢轨受力相等，即：Fn=J。

将式(1)、式(2)分别代入上式后整理可得

式中，1 520 mm宽轨对应的S1=1 600 mm，g取9.81 N/s2，代入并变换量纲单位得

(3)

式(3)即为适用于1 520 mm宽轨的外轨超高公式。其中，V单位为km/h，R单位为m。

2.3 欠(过)超高理论

列车运行中，通过曲线的各次列车，其速度不尽相同。特别是高速铁路存在高、低速匹配问题时，设计超高不能同时平衡高速列车和低速列车通过时的离心力。

(1)当列车速度相对较高时，离心力大于实设超高后所能提供的向心力，离心力未被完全平衡，说明超高设置不足，导致外轨承受轮载较大，磨耗较多，同时也因为离心力未被平衡旅客舒适度下降。此时，按列车通过曲线的速度计算所得超高值大于实设超高的差值称为欠超高(实设超高不足)。

(2)当列车速度相对较低时，离心力小于实设超高后所能提供的向心力，说明超高设置过大，导致内轨承受轮载较大，磨耗较多，旅客舒适度下降。此时，按列车通过曲线的速度计算所得超高值小于实设超高的差值称为过超高(实设超高过大)。

当平面曲线半径和超高一定时，列车以不同速度通过，可能会产生过超高或欠超高，欠(过)超高值不应过大。因此在设置超高时，应该根据列车行驶速度以及高、低速列车的速差，统筹考虑欠(过)超高的影响，使得不同速度的列车通过曲线时，欠(过)超高既能相对均衡，又能满足绝对数值不超限，以达到列车运行安全舒适的目的。

2.4 缓和曲线长度计算公式

对于缓和曲线普遍较长的高速铁路，由脱轨安全要求计算的缓和曲线长度不起控制作用，设计高速铁路缓和曲线长度主要考虑其他两个条件。

(1)乘坐舒适度允许的未被平衡横向加速度时变率要求的缓和曲线长度

式中VG——设计最高速度，km/h；

[β]——旅客舒适度允许的欠超高时变率限值，mm/s，良好条件取23 mm/s，困难条件下取38 mm/s；

hq——圆曲线设计欠超高，mm。

(2)乘坐舒适度允许的车体倾斜角度(即超高时变率限值)要求的缓和曲线长度

式中VG——设计最高速度，km/h；

[f]——旅客舒适度允许的超高时变率限值，mm/s，优秀条件取25 mm/s，良好条件下取28 mm/s，一般条件下取31 mm/s；

h——圆曲线设计超高，mm。

缓和曲线长度取L1和L2中较大值。

2.5 判定条件

由于缺少实测数据，相关国家也缺乏宽轨高速铁路研究经验，本文在研究平面曲线参数与列车行驶安全性和旅客舒适度之间的关系时，采用了我国高速铁路规范标准体系的判定方法。

我国高速铁路规范的设计参数选择中，判定平面曲线设计参数是否满足行车安全和旅客舒适度的条件主要包括：最大设计超高允许值[h]、欠超高允许值[hq]、过超高允许值[hg]、欠超高与过超高之和的允许值[hq+hg]、设计超高与欠超高之和的允许值[h+hq]和旅客舒适度允许的超高时变率限值[f]。根据长期大量的试验研究结果和高速铁路工程实践经验，我国高速铁路规范确定了上述参数与列车安全行驶和旅客舒适度之间的关系，给出了以下判定条件[2]。

(1) 最大设计超高允许值[h]

最大设计超高允许值[h]主要取决于列车在曲线上停车时的安全、稳定和旅客乘坐舒适度要求。国际上高速铁路的最大超高一般在170～200 mm，我国最大设计超高允许值采用175 mm，即[h]=175 mm。

(2) 欠(过)超高允许值

一般认为高速铁路过超高与欠超高对旅客乘坐舒适度的影响是同等的[1]，过(欠)超高允许值主要取决于旅客乘坐舒适度要求，其取值如表1所示。

表1 过(欠)超高允许值 mm

(3)欠(过)超高之和的允许值

欠(过)超高之和的允许值[hq+hg]主要反应速差对曲线半径和超高的影响，其取值如表2所示。

表2 欠(过)超高允许值超高允许值 mm

注：括号内数值为设计行车速度250 km/h与160 km/h匹配时的采用值。

(4)设计超高与欠超高之和的允许值[h+hq]

设计超高与欠超高之和的允许值[hq+hg]主要反映高速对曲线半径和超高的影响，其取值如表3所示。

表3 设计超高与欠超高之和的允许值 mm

3 计算与分析

3.1 确定速度目标值

由于高速铁路的运输组织模式为高速与低速列车共线运行，因此我国高速铁路规范体系中存在速度匹配关系。本文在研究平面曲线设计参数时，采用我国高速铁路规范体系相同的速度匹配关系。通过计算350/250 km/h，300/200 km/h，250/200 km/h，250/160 km/h这四种速度匹配关系的曲线半径、超高、缓和曲线长度，得出平面曲线设计参数研究结论。

3.2 确定半径取值范围和设计超高

由已知理论和经验可知，曲线半径越大越能满足高速铁路通过要求。本文在研究中，采用曲线半径由大到小的顺序进行计算，同时设置较为合理的设计超高，以尽量达到欠(过)超高均衡。但考虑线路测设精度和轨道检测精度，曲线半径不宜过大，故取最大曲线半径为12 000 m。

3.3 计算结果

根据上述研究理论和方法，计算得350/250 km/h的平面曲线设计参数结果如表4所示。

表4 350/250 km/h超高设计、检算

计算缓和曲线长度如表5所示。

表5 350/250 km/h缓和曲线长度

同理计算得速配为300/200、250/200、250/160 km/h结果如表6～表11所示。

3.4 结果分析

3.4.1 平面曲线半径

以350/250 km/h为例，分析计算表4可得如下结论。

(1)当9 000 m≤R≤12 000 m时，欠、过超高为30～43 mm，基本满足乘坐舒适度“优秀”条件；欠、过超高之和为63～84 mm，说明乘坐舒适度为“优秀”；设计超高与欠超高之和为128～171 mm，乘坐舒适度达到“优秀”，因此此区间乘坐舒适度总体评价为“优秀”。

表6 300/200 km/h超高设计、检算

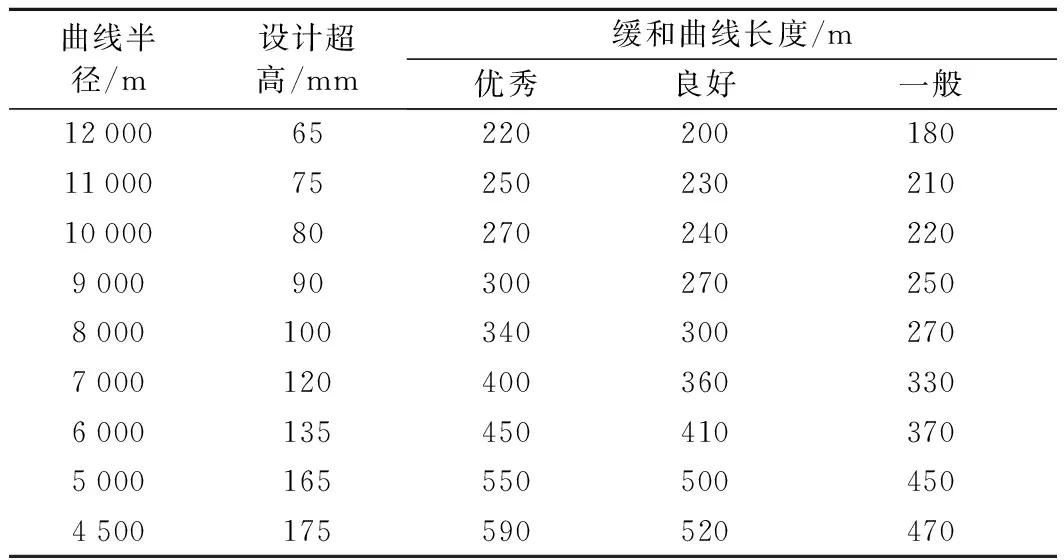
表7 300/200 km/h缓和曲线长度

表8 250/200 km/h超高设计、检算

表9 250/200 km/h缓和曲线长度

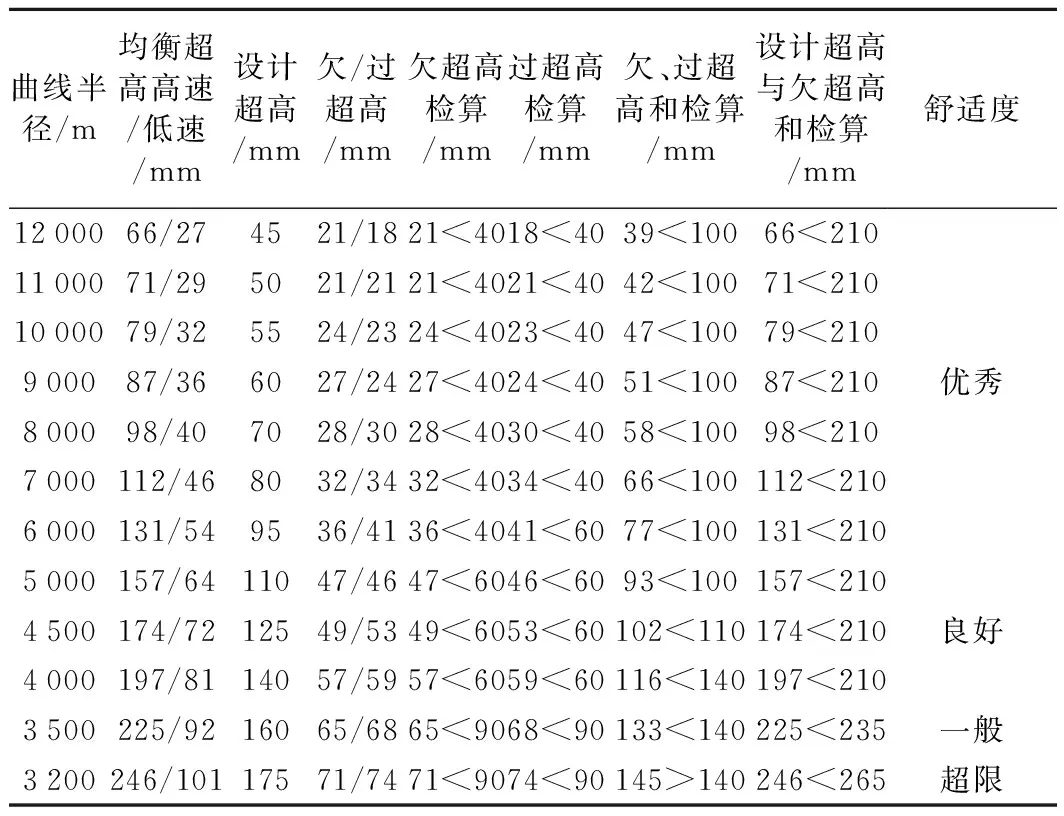
表10 250/160 km/h超高设计、检算

表11 250/160 km/h超高设计、检算

(2)当7 000 m≤R<9 000 m时，欠、过超高为41～55 mm，达到乘坐舒适度“良好”条件；欠、过超高和为84～108 mm，设计超高与欠超高和为171～220 mm，达到旅客舒适度“优秀—良好”条件，总体而言，旅客舒适程度达到“良好”标准。

(3)当6 000 m≤R<7 000 m时，欠、过超高为53～82 mm，达到乘坐舒适度“一般”条件；欠、过超高和为108～126 mm，说明乘坐舒适度为“良好”；设计超高与欠超高和为220～257 mm说明乘坐舒适度为“一般”，因此总体而言，旅客舒适程度为“一般”。

(4)当R<6 000 m时，hq>[hq]一般值=90 mm，欠超高已超过允许值，无法满足旅客舒适度要求，可见平面曲线半径不应小于6 000 m。

(5)当R=5 500 m时，由于受到设计超高h≤[h]=175 mm的限制，已不能通过增大设计超高达到减小欠超高hq的目的，导致欠超高hq>允许欠超高[hq](一般值=90 mm)。此时，最小曲线半径受到最大设计超高允许值[hq]和最大欠超高允许值[hq]的限制，反映出速度要求决定了平面最小曲线半径的取值。同理，300/200 km/h，250/200 km/h也呈现这样的特点。但设计速度匹配为250/160 km/h时，在设计超高并没有达到允许欠超高[hq] (一般值=90 mm)的情况下，欠、过超高之和hq+hg就已经超过欠、过超高之和的允许值[hq+hg]([hq+hg]=140 mm)，说明此时速差成为了平面最小曲线半径的决定因素。因此，平面最小曲线半径值不仅与设计最高速度有关，而且受到速度匹配的影响。

3.4.2 缓和曲线长度

通过缓和曲线计算表的比较分析可知， 1 520 mm宽轨高速铁路缓和曲线长度与1 435 mm标轨高速铁路的相应值相同或相近。这与缓和曲线计算公式是相符的。因为根据缓和曲线长度计算公式，当设计速度一定时，缓和曲线长度只与设计超高有关。

4 研究结论

通过总结归纳以上计算和分析结果，适用于1 520 mm宽轨高速铁路的平面曲线设计参数如下。

(1)平面曲线半径(表12)

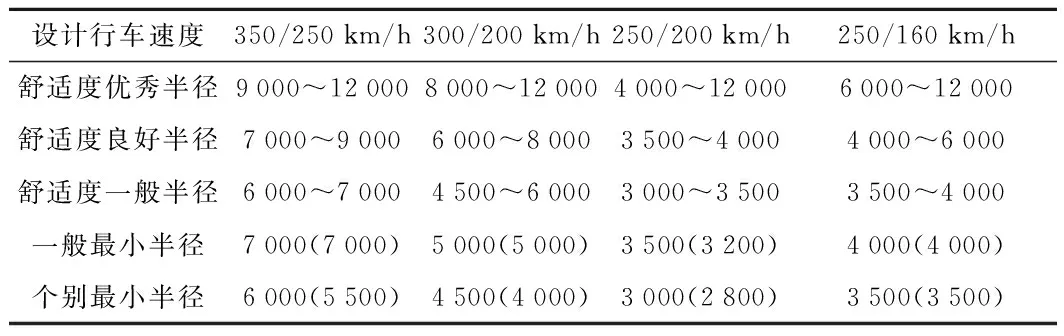
表12 1 520 mm宽轨铁路曲线半径 m

①括号内的数值为相应的1 435 mm标轨取值，在设计速度相同的情况下，宽轨的最小曲线半径大于标准轨的最小曲线半径，而且随着设计速度的减小，这种差距呈逐渐缩小的趋势。

②表中列出了不同设计速度对应的满足不同舒适度条件的曲线半径取值范围。在工程设计中，选择曲线半径应因地制宜、由大到小、合理选用，以使曲线半径既能满足行车速度和设置建筑物的技术要求，又能适应地形地质等条件，减少工程量，做到技术经济合理。在其它条件相当的情况下，应优先选用与速度目标值项目匹配的满足旅客舒适度优秀或良好条件的半径，慎用一般最小曲线半径值。个别最小半径值需进行充分的技术经济比选后方可采用。

(2)缓和曲线长度推荐值(表13)

通过与我国高速铁路设计规范对比可知，1 520 mm宽轨高速铁路缓和曲线取值与1 435 mm标准轨取值相同或相近，缓和曲线长度主要受设计超高和设计速度控制，与轨距基本无关。

(3)1 520 mm宽轨高速铁路最小曲线半径主要受到设计速度和速度匹配的影响，设计速度越高，速差越大，最小曲线半径越大。因此，在工程设计中，要结合业主需求、客货运量特点、行车组织方案等因素，合理确定速度目标值和速度匹配关系，以避免最小曲线半径过大，影响工程投资。

表13 缓和曲线长度 m

5 结语

我国高速铁路还处于“走出去”阶段的初期，对于1 520 mm宽轨的研究才刚刚起步，在缺乏实测数据和工程实践经验的情况下，为尽快推进我国高铁“走出去”战略的实施，本文的研究方法不失为一种合理有效的捷径，也同时为米轨(轨距为1 000 mm)地区我国高速铁路技术的研究和应用提供参考。鉴于线路平面设计参数与车辆技术参数有一定的相关性，具体项目需结合所选车辆情况对本研究提出的结论进行必要的检核或修正[13]。

同时，随着“一路一带”战略的继续推进，我国铁路相关部门应该同相关国家铁路部门一道，就宽轨高速铁路展开广泛而深入的合作，修建高速铁路试验段，测试相关参数数据，积累建设运营经验，编制广泛认可的1 520 mm宽轨高速铁路设计规范，为我国高速铁路技术在宽轨地区的应用和推广奠定良好的基础。

[1] 中华人民共和国铁道部.TB10621—2009高速铁路设计规范(试行)[S].北京：中国铁道出版社，2010．

[2] 中华人民共和国铁道部.TB10621—2009高速铁路设计规范(试行)条文说明[S].北京：中国铁道出版社，2010．

[3] 郝瀛，易思蓉，何华武，等.铁道工程[M].北京：中国铁道出版社，2013．

[4] 崔显付.吉图珲客运专线平面曲线参数设计研究[J].铁道标准设计，2014，58(9)：5-9．

[5] 李嘉伟，秦宝清.宽轨机车动力学安全性试验分析[J].铁道机车车辆，2013，33(6)：36-38．

[6] 罗世辉.轨距对机车车辆稳定性影响研究[J].中国铁道科学，2010，31(2):56-60.

[7] 谷爱军.铁路轨道[M].北京：中国铁道出版社，2004．

[8] 王其昌.高速铁路土木工程[M].成都:西南交通大学出版社，2000.

[9] 王午生.铁道线路工程[M].上海:上海科学技术出版社，1999.

[10]铁道科学研究院铁道建筑研究所.高速铁路平立面曲线参数的初步研究[R].北京:铁道科学研究院铁道建筑研究所，1995.

[11]Louis TKlauder Jr. Improved Spiral Geometry for High Speed Rail[A]. In: Proceedings of the 2000 annual conference of the American Railroad Engineering and Maintenance of Way Association[C/CD]. Landover MD: AREMA， 2000．

[12]同济大学铁道建筑工程系.缓和曲线与曲线超高及竖圆重叠试验研究[R].上海:同济大学铁道建筑工程系，2003.

[13]白宝英.《城际铁路设计规范》之线路设计标准解读[J].铁道标准设计，2015，59(3):29-32.

Study on Design Parameters of Plane Curve for 1 520 mm Broad Gauge High-speed railway

WANG Shi

(China Railway Eryuan Engineering Group Co.， Ltd.， Chengdu 610031， China)

This paper aims to provide a reference for the calculation and design of plane curve design parameters applicable to regions with 1 520 mm broad gauge railway.

High-speed railway; 1 520 mm broad gauge; Design parameters of plane curve

2015-01-21；

2015-02-22

王 诗(1984—)，男，工程师，2011年毕业于兰州交通大学

道路与铁道工程专业，工学硕士，E-mail:d_shi_wang @163.com。

1004-2954(2015)10-0027-06

U238; U212.33

A

10.13238/j.issn.1004-2954.2015.10.007

Based on calculation methods and decision conditions of china high-speed railway design code， this paper calculates the plane curve design parameters of 1 520 mm broad gauge high-speed railway and analyzes the influence of different plane curve radius and super-elevation values on train operation and passengers’ comfort. The range of reasonable radius， the minimum curve radius and transition curve values at different speeds are obtained.

Research conclusion: (1)The minimum curve radius of 1 520 mm broad gauge high-speed railway are influenced mainly by the designed speed and matched speed. The higher the design speed， the greater the speed difference and the minimum curve radius are. (2)Under the same condition， the minimum curve radius of 1 520 mm broad gauge railway is greater than that of the standard gauge. (3)Transition curve values are mainly controlled by designed super-elevation and speed in independent of the gauge.