初始不平顺与初始弯曲的叠加方式对无缝线路稳定性影响

罗华朋，马旭峰，王 平，谢铠泽

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

初始不平顺与初始弯曲的叠加方式对无缝线路稳定性影响

罗华朋，马旭峰，王 平，谢铠泽

(西南交通大学高速铁路线路工程教育部重点实验室，成都 610031)

针对无缝线路稳定性方面的分析，研究线路初始不平顺与初始弹塑性弯曲之间的叠加方式具有重要意义。根据无缝线路稳定性有限元分析理论建立钢轨、扣件、轨枕和道床阻力为一体的轨道框架模型，对于桥上无缝线路由于梁端相对伸缩产生的线路不平顺，分析线路不平顺幅值位置以及各弦测法对应矢度最大值位置与初始弹塑性弯曲的叠加线型对无缝线路稳定性的影响。分析表明：梁端横向伸缩引起的钢轨变形会降低无缝线路的稳定性。建议对于存在初始不平顺的线路，首先采用4 m弦长对线路初始不平顺进行测量，得到最大的矢度对应的位置，然后与钢轨初始弹塑性弯曲最大处相对应进行叠加，最后进行求解，以此作为计算无缝线路稳定性最不利的工况。

无缝线路；稳定性；有限元分析理论；初始弯曲

有砟无缝线路最突出的问题就是由于它在结构上限制了钢轨的伸缩，当温升较大时，钢轨内积聚巨大的温度力，当压力达到一定值时，有可能造成轨道的臌曲，亦即丧失稳定。对于无缝线路稳定性的分析，主要有微分方程法[1-2]、能量法和有限元法。相对于微分方程法和能量法，由于有限元法在不假设钢轨变形曲线条件下可以考虑各种材料、边界条件及几何关系等引起的非线性，并且能模拟出各种线路条件下从稳定状态发展到失稳状态的过程，因此许多学者对该方法进行了研究。周毅等[3-4]采用有限单元法几何非线性理论分析了直线上、曲线上无缝线路失稳的影响因素，杨冠岭[5]首次采用有限元方法分析大跨桥上无缝线路竖向稳定性问题，但是这些研究均未分析线路存在初始不平顺，以及初始不平顺与弹塑性初始弯曲的叠加方式对稳定性的影响。因此，就线路不平顺与初始弹、塑性弯曲之间的具体叠加方式展开讨论，分析确定稳定性影响最不利的叠加方式，从而得到线路容许升温值。

1 无缝线路稳定性有限元计算模型

无缝线路在温度力作用下发生横向臌曲的力学模型如图1所示。该模型以普通的平面梁单元模拟钢轨和轨枕，且考虑了钢轨梁单元和轨枕梁单元剪切变形以及钢轨梁单元非线性变形的影响；利用线性弹簧单元模拟钢轨与轨枕的扣件之间的纵向、横向以及扭转阻力；利用非线性弹簧单元模拟道床的纵横向阻力。

图1无缝线路横向臌曲的有限元模型

2 稳定性模型中横向不平顺与初始弯曲的叠加

2.1 初始横向不平顺

为了研究稳定性模型中初始横向不平顺与初始弹塑性弯曲的叠加作用，引用桥上无缝线路由于梁端相对伸缩引起的钢轨横向变形作为线路初始不平顺。

由于钢桥与混凝土桥线膨胀系数、温差变化、支座间距等存在一定的差异，在桥梁温度变化时会引起钢轨发生不同横向位移，由于该位移的存在因而钢桥与混凝土桥连接处梁端横向位移差别最大。具体计算工况为[6]：与钢桥相连的是跨度32 m的混凝土简支梁桥，弹性模量E=3.45×104MPa，热膨胀系数α=1.3×10-5/℃，ΔT为15 ℃；钢桁梁的弹性模量E=2.06×105MPa，热膨胀系数α=1.18×10-5/℃，ΔTS为25 ℃。计算钢轨在梁体升温条件下产生的横向变形如图2所示。

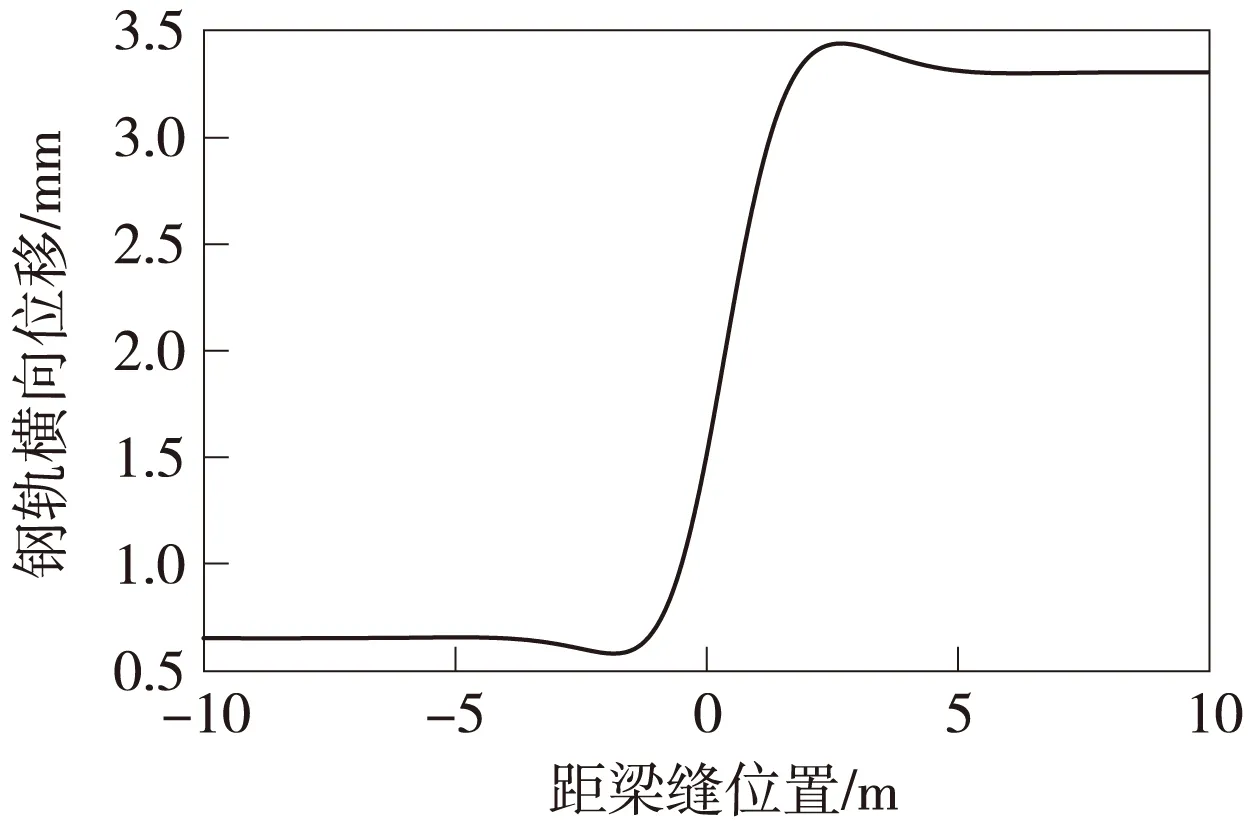
图2 钢轨横向变形

2.2 横向不平顺与初始弯曲的叠加线型比较

把梁端横向伸缩引起的钢轨横向变形作为线路初始条件，然后在路基上建立图1所示的无缝线路稳定性模型，分析钢轨横向变形与初始弯曲叠加的问题。由于主要讨论的是初始弹塑性弯曲与梁端钢轨横向变形的叠加，因此暂不考虑圆曲线的叠加。

在有限元方法计算中，弹性初始弯曲采用正弦曲线，塑性初始弯曲采用圆曲线，初始弹塑性弯曲保持恒定，一般假设f0e=f0p=0.3 cm，并且初始半波长均假定为l0=4 m[7-8]，初始弯曲图形如图3所示(图中以矢度最大处对应的为零点)。

图3 轨道初始弹塑性弯曲变形曲线

依据无缝线路稳定性分析的规律及变形特性，拟采用8种方案进行叠加计算，见表1。

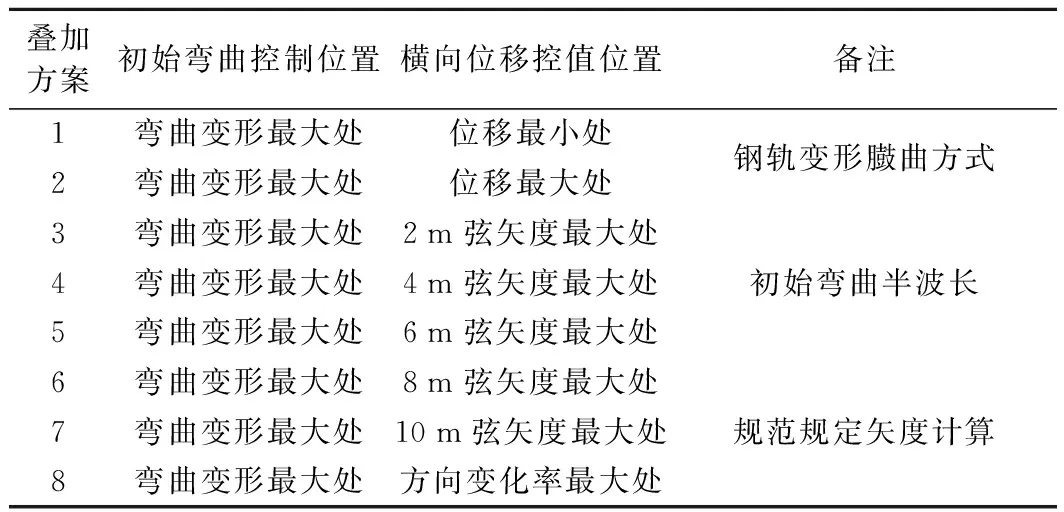
表1 计算方案

基于上述分析，首先要确定钢轨横向变形最大与最小点位置，2、4、6、8 m与10 m弦矢度最大位置及钢轨横向变形方向变化率最大位置，其中钢轨横向变形最小点位置为梁缝位置左侧1.900 m，最大点位置为梁缝右侧2.641 m，2、4、6、8 m与10 m弦测法的结果如图4所示，对应的矢度最大值位置分别为梁缝右侧1.027，1.658，2.055，2.451，2.825 m。钢轨横向方向变化率计算结果如图5所示，图6为钢轨横向变形不同位置与钢轨初始弹塑性不平顺相叠加的结果。

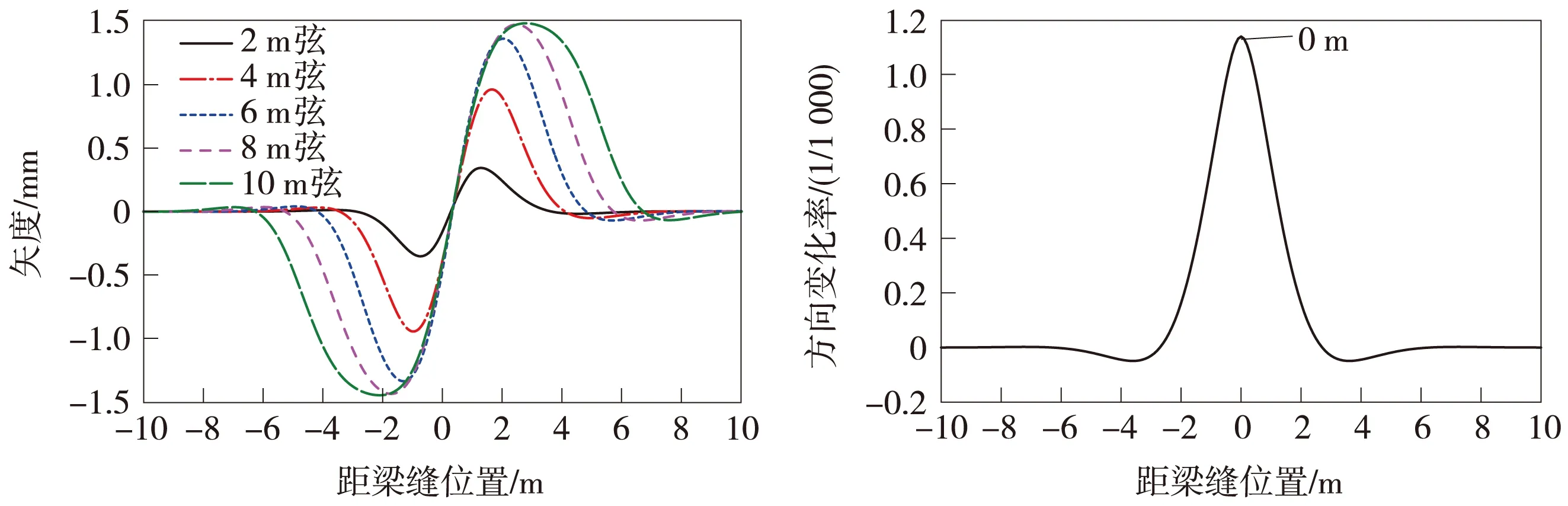
图4 钢轨横向不平顺矢度

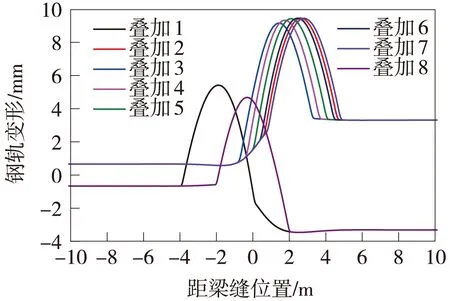
图5 轨道方向变化率

图6 轨道变形曲线

从图6中可以看出，2、4、6、8、10 m弦不平顺矢度最大值对应的图形相差较小，这是因为虽然梁端横向位移引起的钢轨有一定的横向位移，但是相比较而言起主要作用的仍然是钢轨初始的弹塑性弯曲，弹塑性初始弯曲矢度为6 mm，从图4中看出各弦测法对应的矢度均不超过1.5 mm。

2.3 直线上稳定性分析

图7 钢轨横向位移与纵向力关系

对于表1中的其他叠加情况，也采用相同的道床横向阻力进行稳定性计算，其计算结果如表2所示，表中叠加方案0为不考虑梁端横向伸缩引起的钢轨横向变形。

表2 不同叠加工况下的计算结果

表2所示的计算结果表明，无论何种叠加方式相对于不发生梁端横向位移时稳定性均有降低，其中最大降低幅度达到10.36 ℃，因此梁端横向伸缩引起的钢轨变形会降低无缝线路的稳定性。上述8种叠加方式计算结果看出，其中最不利的叠加方式为4 m弦不平顺矢度最大的位置叠加初始弹塑性弯曲最大值位置的工况，其主要原因是该弦长4 m与钢轨弹塑性初始弯曲的半波长相等，这种叠加方式虽然不能保证初始横向位移最大，但能够保证钢轨横向变形曲线与弹塑性初始弯曲曲线重叠部分最多，因此这时的稳定性最差；对于梁端钢轨横向变形最大、最小点与初始弹塑性弯曲最大值位置叠加的工况，虽然能保证钢轨的初始的横向位移最大，但是这时的半波长较大，使得钢轨横向变形曲线与弹塑性初始弯曲曲线重叠较少，因此对无缝线路影响较小，造成的轨温变化幅度降低值也较小。比较上述两种工况，4 m弦不平顺矢度最大的位置叠加初始弹塑性弯曲最大值位置的工况对应的允许升温为69.37 ℃，梁端钢轨横向变形最大位置与初始弹塑性弯曲最大值位置叠加的工况对应的允许升温74.62 ℃，两者相差5.25 ℃，可以看出如果采用以前的叠加方式计算允许升温，计算结果会偏大，使无缝线路稳定性处于非保守状态下。

2.4 曲线上稳定性分析

考虑曲线半径(R=1 000 m)时，保证圆曲线中点与初始弹塑性变形的矢度最大处为同一个位置，同样以钢轨横向变形最大值处与初始弹塑性弯曲最大值处叠加为例，采用相同的道床横向阻力进行稳定性计算，其线路中对应的钢轨横向位移与钢轨纵向力之间的关系如图8所示。

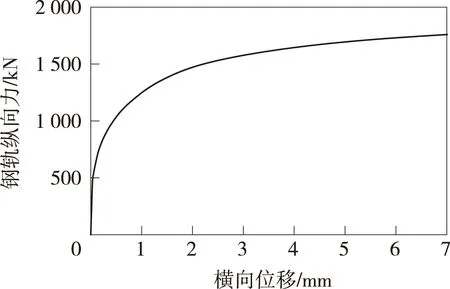
图8 钢轨横向位移与纵向力关系(R=1 000 m)

从图8看出，当横向位移达到2 mm时，对应的单根钢轨纵向力为1 471.70 kN，考虑同样安全系数并转化为钢轨温度变化幅度为63.95 ℃，允许温升明显比不考虑曲线半径影响时小。

其他计算结果如表3所示，同样表中叠加方案0为不考虑梁端横向伸缩引起的钢轨横向位移。

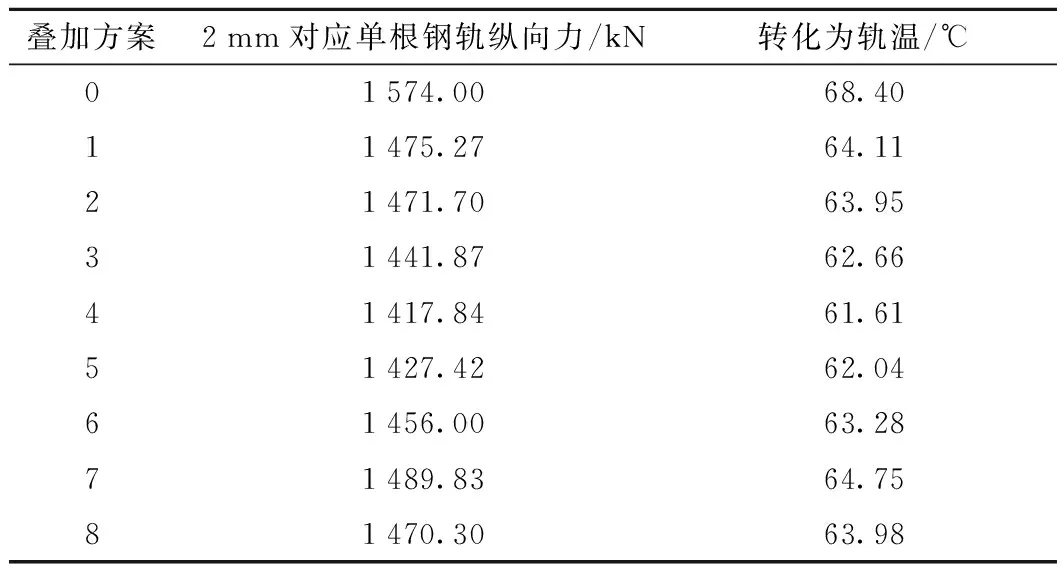
表3 不同叠加工况下的计算结果

从表3计算结果看出：其基本规律与直线上相似，但是由于圆曲线的存在，使得钢轨横向变形对无缝线路的影响有所降低，最大降低幅度为8.14 ℃。此时，4 m弦测法对应矢度最大的位置叠加初始弹塑性弯曲最大值位置的工况对应的允许升温为61.61 ℃，梁端钢轨横向变形最大位置与初始弹塑性弯曲最大值位置叠加的工况对应的允许升温为63.95 ℃，两者仅相差2.34 ℃，可以看出考虑曲线半径的影响，使得钢轨横向变形对稳定性的影响减小，因为考虑曲线半径与初始弹塑性弯曲、钢轨横向变形叠加之后，钢轨横向变形曲线所占比重更小，对稳定性的影响也相对降低。表4为统计结果。

表4 统计结果

从表4统计结果看出，是否存在圆曲线，各种叠加方式的结果变化不大，均是当在4 m弦测量矢度最大位置处于初始弹塑性弯曲(圆曲线)叠加时对无缝线路的影响最大。同时无论对于直线上还是圆曲线上，对无缝线路稳定性影响最小的都是10 m弦测量矢度最大位置处于初始弹性弯曲叠加时，分析其主要原因是10 m弦测量矢度最大位置位于梁缝右2.857 m处，距初始弹塑性弯曲的半波长为4 m所对应的位置偏离较远，使其重叠部分较少，而且也不是横向位移最大处的叠加，不能保证钢轨的初始横向位移最大，所以其对无缝线路的影响较小。

3 结论及建议

通过上面的计算可以得到：(1)梁端横向伸缩引起的钢轨变形会降低无缝线路的稳定性。(2)对于存在初始不平顺的线路，无论是直线上还是曲线上，均是当在4 m弦测量矢度最大位置与初始弹塑性弯曲(圆曲线)叠加时对无缝线路稳定性的降幅最大。(3)基于此原理，对于任意的钢轨横向变形在计算其对无缝线路的稳定性的影响时，均宜以4 m弦矢度最大处为基准，与初始弹塑性弯曲进行叠加来检算无缝线路的稳定性。

[1] Kish A， Samavedam G， Jeong D. Analysis of Thermal BuckingTests on U.S.Railroads[R]. Technique Report， NTIS-PB83-203554， 1982:21-102．

[2] Samavedam G， Kish A， Purplre A. Parametric analysis and safety concepts of CWRTrack bucking[R]. Final Report， NTIS-PB94-154648， 1993:38-109．

[3] 周毅.无缝线路温度臌曲失稳过程的有限元分析[J].中国铁道科学，1988(2):12-20．

[4] 罗信伟.小半径曲线无缝线路稳定性有限元分析[J].铁道工程学报，2006(3):8-12.

[5] 杨冠岭.高墩大跨桥上有砟轨道无缝线路稳定性研究[D].成都：西南交通大学，2009:43-58．

[6] 王平，陈嵘，杨荣山，等.桥上无缝道岔设计理论[M].成都：西南交通大学，2011．

[7] 王平.冻结无缝线路稳定性[J].西南交通大学学报，2000(10):460-464．

[8] 广钟岩，高慧安，陈岳源，等.铁路无缝线路[M].北京:中国铁道出版社，2010：63-71．

[9] 中华人民共和国铁道部.TB10015—2012铁路无缝线路设计规范[S].北京:中国铁道出版社，2013．

[10]冯青松.无缝线路稳定性分析有限元模型[J].铁道标准设计，2004(11):13-16．

[11]张小勇.车辆荷载对无缝线路稳定性的分析[J].铁道建筑，2008(2):90-93．

[12]广钟岩，高慧安.铁路无缝线路[M].北京:中国铁道出版社，2005：21-189．

[13]段固敏.曲线轨道无缝线路呼吸及弹动机理分析[J].铁道学报，1996(1):84-89．

Effects of Initial Irregularity and Initial Bending Stacking on the Stability of Continuous Welded Rail

LUO Hua-peng， MA Xu-feng， WANG Ping， XIE Kai-ze

(MOE Key Laboratory of High speed Railway Engineering， Southwest Jiaotong University， Chengdu 610031， China)

Analysis of the stability of continuous welded rail is conducted to understand the initial track irregularity and initial elastic-plastic bending’s superposition. Based on CWR track stability finite element analysis theory， a track framework model is established in perspective of the rail， fastening， sleeper and roadbed resistance to analyze the effects of the track initial irregularity and initial elastic-plastic bending’s superposition on the stability of continuous welded rail with respect to the track irregularity produced by beam end relative extension. Analysis shows that the track initial irregularity may reduce track stability. Suggestions for the presence of track initial irregularity are made to use 4m chord to measure the track initial irregularity for the maximum position relating to the vector， and then stack with the rail initial elastic-plastic bending， and the solution is taken as the worst condition of the stability of continuous welded rail．

Continuous welded rail; Stability; Theory of finite element analysis; Initial bending

2014-10-08

中央高校基本科研业务费资助项目(SWJTU12CX079)

罗华朋(1991—)，男，硕士研究生，E-mail:756468322@qq.com。

1004-2954(2015)07-0040-04

U213.9+11

A

10.13238/j.issn.1004-2954.2015.07.010