基于L型网络的高效无源阻抗匹配研究*

邵蕊娜，张峻梓，李风光，闫 钧

(河南省医疗器械检验所，河南郑州 450003)

0 引言

在高频加热电源、电磁超声探伤检测等高频逆变电源的实际应用中，阻抗匹配是一个必备的关键环节［1］。一方面，阻抗匹配程度决定了传递到负载的功率大小，另一方面，阻抗匹配网络本身的损耗也决定了系统的整体效率，这一点在高频下显得尤为突出［2］。阻抗匹配网络往往由多个器件组成，各个器件的品质因数和网络结构决定了其功率传递效率，即:不同结构的网络可以实现同一阻抗匹配功能，但往往只有一种结构具有最高效率［3］。针对阻抗匹配网络的研究向来备受关注，但学者们的关注点主要集中在频响特性方面，关于效率最优化理论和设计方法的研究却并不多［4］。笔者试图从最基本的L型网络入手，研究阻抗匹配网络效率最大化的理论和设计方法，并通过实验进行验证。

1 高效L型阻抗匹配网络研究

无源二端口阻抗匹配网络有三种基本结构:L型、Π型和T型，Π型和T型网络可由L型网络级联得到，因此从 L型网络入手研究，具有基础性意义［5］。根据元件性质(电感或电容)的不同，L型网络有两种基本形式:C-L低通型(低通滤波器)和LC高通型(高通滤波器)，如图1所示，其中，C11、L12、L11、C12为组成L型网络的电抗元件;ESRC和 ESRL分别为电容和电感的串联等效电阻(Equivalent Series Resistor，ESR)［6］。定义电感品质因数为 QL= ωL/ESRL，电容品质因数为 QC=1/(ωC·ESRC);Rz和Ry分别为从左侧和右侧看进去的电阻，在阻抗变换中，一个是已知电阻，另一个是阻抗变换目标电阻;Vz、Iz分别为左端口的输入电压和输入电流的有效值，Vy、Iy分别为右端口的输入电压和输入电流的有效值［7］。

图1 L型网络的两种基本结构

根据阻抗匹配网络理论，定义阻抗变换因数Q、左端口品质因数Qz和右端口品质因数Qy如式(1)～(3):

式中:ω为网络中交流电能的角频率。以图1(a)为例，研究阻抗变换的基本条件。已知Ry，求将Ry变换为Rz的条件，基本方程为:

对式(6)进行分析化简，可得:

由此容易证明，对于 L型网络，忽略 ESRC和ESRL的影响，实现Rz与Ry之间阻抗变换的充要条件为式(7)。

定义L型网络左侧的输入功率为Pz，右侧的输入功率为Py，显然有:

对于C-L低通型网络，若左侧接电源、右侧接负载，则 Pz＞0，Py＜0，ESRC上的损耗 PEC和 ESRL上的损耗PEL分别为:

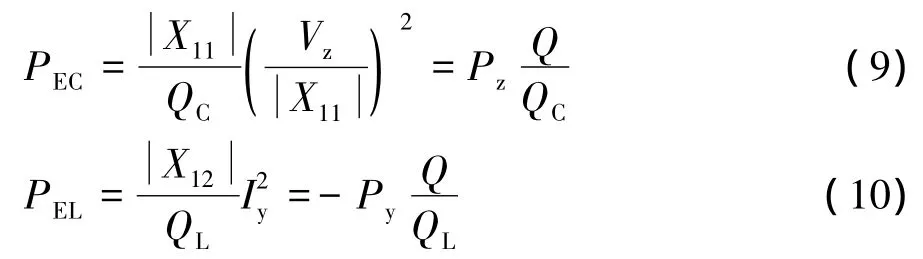
C-L低通型网络的效率ηCL-1为:

同理，当右侧接电源，左侧接负载时，C-L低通型网络的效率ηCL-2为:

对于L-C高通型网络，其左侧接电源、右侧接负载时的效率ηLC-1和右侧接电源，左侧接负载时的效率ηLC-2分别为:

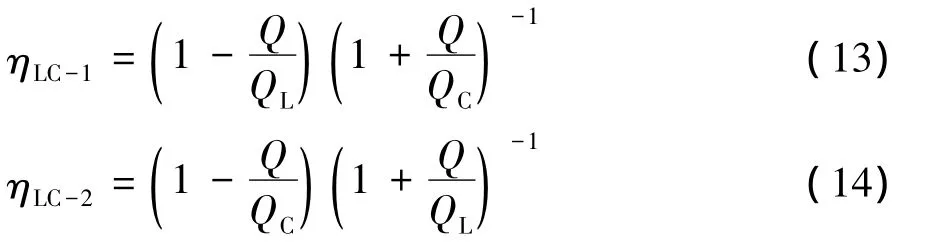
由式(11)～(14)可知，ηCL-1和 ηLC-2有相同的表达式，ηCL-2和ηLC-1有相同的表达式。通常情况下，Q≪QL≪QC，于是:

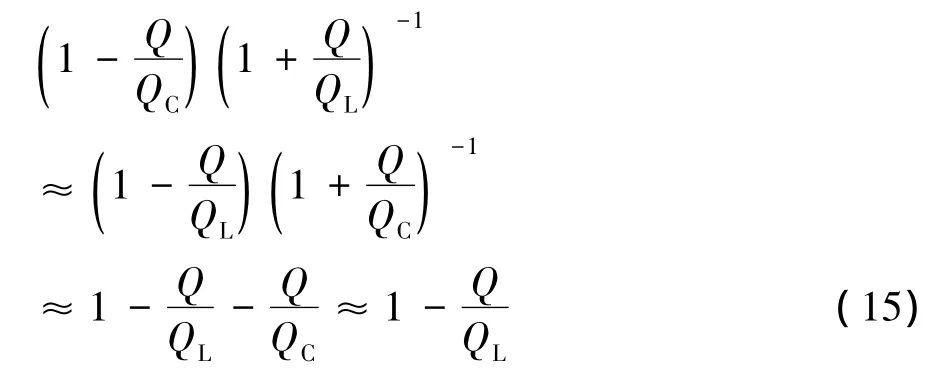
由此，C-L低通型网络和L-C高通型网络的传输效率η的表达式可统一近似为:

由式(16)容易看出，η与阻抗变换因数Q成反比，与电感的品质因数QL成正比，因此，为了实现较高的匹配效率，应当减小阻抗变比，并采用高品质因数的电感器件。

由式(16)还可以看出，当阻抗变比较大导致Q较大，可与QL比拟时，η会非常小，单级L型网络可能由于损耗严重无法正常工作，此时可采用多个L型网络级联的方式分散损耗［8］。容易证明，各级联网络的阻抗变比之积应等于总的阻抗变比。记级联网络的个数为n，第i个网络的阻抗变换因数为Qi，则整个级联系统的效率为:

通过数学分析可得，n级L型网络的总效率的最大值ηn-max为:

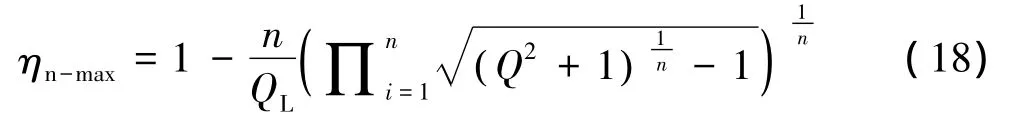
可以证明，当n趋于［ln Q］(［ln Q］表示对ln Q向上取整)时，ηn-max取得最大值ηmax，若记nopt=［ln Q］，则:

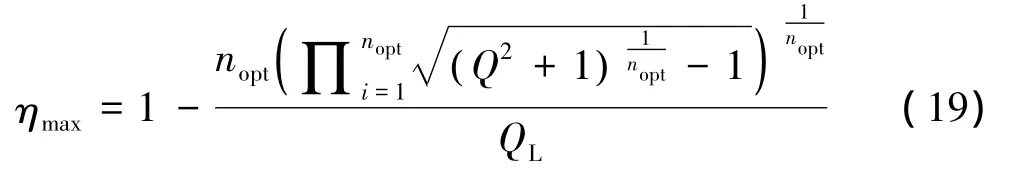
由上述分析可知，当Q＜2．718时，采用单级L型网络具有最高效率，当 2．718＜Q＜7．389 时，采用两级L型网络具有最高传输效率，且每级的阻抗变换因数为。根据式(1)，当目标阻抗变比介于1∶1与8．389∶1之间时，采用单级L型网络具有最高效率;当目标阻抗变比介于8．389∶1与55．6∶1之间时，采用两级L型网络具有最高效率。因此，当目标阻抗和已知阻抗的比值小于55．6时，阻抗匹配网络最多需要4个电抗器件，具有很强的实用性和经济性。

2 实验

根据前述理论分析，对某型医疗器械用高频逆变系统的阻抗匹配网络进行了实验设计与测试，电路如图2所示［9］。逆变电源输出频率 f=2．6 MHz的方波，Z0为纯阻性负载，阻抗匹配网络在进行阻抗变换的同时，还要对逆变器输出的方波信号进行滤波，方便起见，将其称作Mnet。逆变电源可被等效为一个电动势为E、内阻为ρ的交流电源，阻抗匹配网络的输入输出关系如图3所示。ρ的大小由逆变器MOSFET Q1和Q2的导通电阻决定，它和逆变器的输出功率决定了Ri的值。Mnet的阻抗变比为Ri/Z0。

图2 高频逆变器用阻抗匹配网络

图3 阻抗匹配网络的输入输出关系

考虑到Mnet应具有带通滤波作用，其结构可通过两种L型网络的级联实现。为了确保匹配效率的最大化，各级电路应保持相等的Q值，且网络级联的个数nopt-1为:

在式(21)中，当 nopt-1＞2 时，Ri/Z0＞8．389。通常情况下，Ri和Z0的比值一般小于8．4，因此，取nopt-1=2，即Mnet的结构是一个C-L低通型和一个L-C高通型的级联。电路拓扑如图4所示。

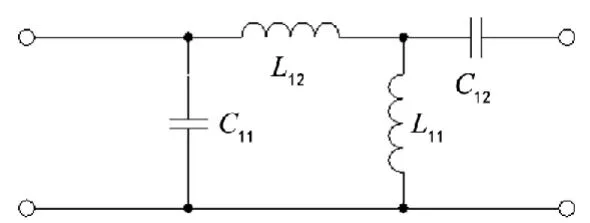
图4 Mnet的拓扑结构

实验电路参数如表1所列，其中Z0为f=2．6 MHz下的阻抗值，可近似看做纯电阻;实验电路如图5所示，其中虚线框部分为逆变电源电路，实线框部分为阻抗匹配电路。电路中电感期间均采用低磁导率镍锌磁环绕制而成，电容器件采用TDK CK45-RR±10%1-3 kV陶瓷电容。Z0和Q的值均为阻抗分析仪在2．6 MHz下的测量值。

表1 实验电路参数

使用Tektronics TPS2014四通道隔离示波器、Tektronics P6015A高压差分探头、Tektronics TCPA300电流探头、Tektronics TPS2PWR1功率分析模块等进行功率测量。逆变器的输入功率为50．1 W，输出功率为47．6 W，负载功率为45．4 W，阻抗匹配电路的效率为95．37%，超过了92%的规定效率，在2．6 MHz下，该效率值比较理想。

图5 实验电路

3 结论

基于无源L型网络的效率特性，研究了阻抗匹配网络效率最大化的问题，推导出由多个L型网络级联而成的阻抗匹配网络具有最大效率的条件是级联网络的个数为［ln Q］(Q为阻抗变换因数)，且每级

表4 BP神经网络测试输出样本

［1］ 杨树莲．BP神经网络在齿轮箱故障诊断中的应用［J］．机床与液压，2006(7):244．

［2］ 张绪锦，谭剑波，江 洪．基于 BP神经网络的故障诊断方法［J］．系统工程理论与实践，2002，22(6):61-66．

［3］ 李培元，谢志江，赵心夏．基于BP神经网络的大型旋转机械故障诊断及其网络数据源的研究［J］．西南民族大学学报:自然科学版，2004(3):23．

［4］ 魏 勇．基于具有模糊输出BP网络的决策分类模型的研究:(硕士学位论文)．北京:北京工业大学，2002:20-25．

［5］ 贾玉玲，邱惠清．BP神经网络齿轮故障诊断的仿真［J］．机床与液压，2008，36(7):229-230．

［6］ 刘君华．智能传感器系统［M］．第2版．西安:西安电子科技大学出版社，2010．