B类宏程序在斜度数控加工中的应用分析*

马士伟

(烟台汽车工程职业学院，山东烟台 265500)

0 引言

对于斜度零件的加工方式，目前主要有三种:一是运用斜度铣刀，如图1所示，即通过带斜度的刀刃直接切削，二是修砂轮法，三是线切割。这三种加工方式都有各自的优缺点，使用斜度铣刀加工时对刀刃的要求较高，限制了斜度的参数设计的灵活性;修砂轮法主要应用于斜面面积小且斜度在槽内面，具有一定的局限性;线切割方法加工精度高，但效率低。而运用宏程序在数控加工中心上便可以很好的完成斜度的加工，既满足了精度要求，又提高了效率，加工的范围广，实现了由刚性制造到柔性制造的转变，极大改善了斜度的加工工艺，节省了成本［1］。

1 斜度的形状分析

斜度是指一直线(或一平面)对另一直线或(一平面)的倾斜程度。其大小用他们之间的夹角正切来表示。斜度为tanα=H/L，习惯上把比例的前项化为1而写成1∶n的形式。标注斜度时，符号方向应与斜度的方向一致，如图2所示。

图1 斜度铣刀

图2 斜度简图

在斜度的数控加工中，编程的难度在于随着加工位置的改变，切削的余量在不断改变，而且对于存在多个斜面的零件，在数控铣床上进行加工需要不断变换工件的位置，这样就增大了工件的加工误差。根据这一特点，采用数控加工中心进行加工，根据零件的具体结构、形状选择合适的铣刀，针对有深度并且斜度大的型面应先粗铣去除多余材料后再加工，防止加工时产生避刀现象，对于带有多个斜面的零件，应先将其中的一个斜面加工出来，然后采用G68坐标系旋转功能，将其余斜面加工出来［2］。

2 斜度宏程序的过程分析

宏程序编程，简而言之，就是用变量的方式进行编程的方法，与一般的程序比较而言，普通程序的程序字是常量，不可变化，一个程序只能描述某个固定不变的几何轮廓，而宏程序通过操作人员对程序的编制，可实现变量的时刻变化，从而达到可以执行一些具有规律性的变化动作［3］。B类宏程序类似于C语言的编程，编写起来很方便，适合于编写一些非圆曲线，比如:双曲线、椭圆、斜面等，在编写相似程序条时，仅需改变几个数据就可以，简单方便［4］。

以一个典型的斜度零件为例，如图3所示，倾斜角度为82°，工件四面都有斜度。

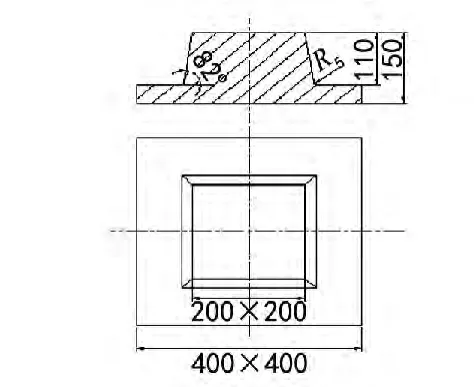
图3 典型斜度零件

2．1 宏程序的控制语句

宏程序的控制指令起到控制程序流量的作用，主要有无条件转移语句和条件转移语句。

(1)无条件语句

格式:GO TO N

例:GO TO 200

表示当执行到该流程时，将无条件的转移到N200的程序段的位置执行。

(2)条件转移语句(也叫IF语句)

格式:IF［条件表达式］GO TO N

例:IF［#1 NE 20］GO TO 200

表示当#1不等于20的时候，转移到N200的程序段开始执行，当#1=20的时候，程序继续向下执行［5］。

2．2 刀具选择及刀偏计算

(1)刀具选择 对于根部带有R弧要求的斜面加工最好使用球头铣刀，使用球头铣刀来加工光洁度比其他铣刀要好，并且球头铣刀没有刀具补偿，加工效率高，根据工件的具体尺寸形状，选择R5的球头铣刀。

(2)刀偏计算 球头铣刀没有刀具补偿，但有刀偏。球头铣刀在铣削加工时，是其端部的圆弧与工件接触而不是刀具的中心，因此，接触点与刀具的中心有一段距离，称为刀偏，如图4所示。根据刀偏的计算公式:

H=R×cosα-［R-R×sinα］×tanα式中:H为刀偏;R为刀头半径;α为斜度。

求得:H=0．34 mm。

图4 球头铣刀刀偏

3 加工工艺过程分析及程序编制

3．1 加工工艺过程分析

在进行斜度加工时，需要2．5轴联动，即在每一时刻3轴中仅需实现2轴联动，另一轴是点位或直线控制，球头铣刀在Z轴方向上进行深度变量的选取，每下沉一个深度变量，在X、Y两轴的平面内进行直线铣削。具体加工过程:先加工出其中的一个斜面，然后通过G68命令将工件旋转，以便加工出其余的斜面。

(1)如图5是零件在XY平面内的走刀路线。

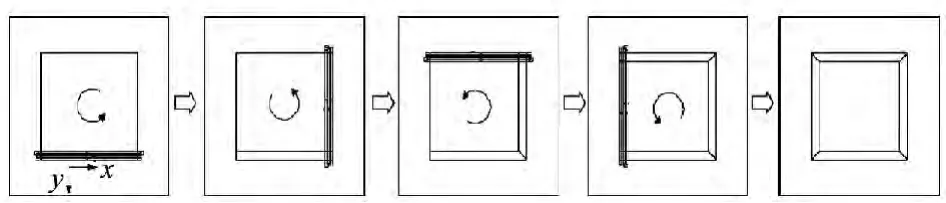
图5 走刀路线

(2)在Z方向上，进行深度变量的选取，为了保证斜面加工的精度，加工斜面落料要小，每次下移0．2 mm，即Z=0．2 mm，同时计算出Y轴方向的外移量，Y=0．2/tan 82=0．03 mm，即 Z 轴方向上每下移0．2 mm，在 Y轴方向上依次累加0．03 mm，如图6。

图6 刀具深度变量局部图

3．2 程序编制及相关解释

根据上述分析，铣削四面斜度的程序如下:(FUNAC数控系统)

G54 G00 G40 G49 G80 Z100 S1200 M03;

#1=0;(度数变量)

N100 G00 X-125 ．Y-104．66;(定位)

G00 Z0;(平面)

#2=0．2;(深度变量)

N200#3=#2×TAN［82］;(每次Y轴向外的移动量)

#4=130+#3;(Y轴坐标)

G01 X-125．Y-#4 Z-#2 F100;

G01 X125．F1000;

#10=#2+0．2;(深度变量累加)

#5=#10 ×TAN［82］ #6=130+#5;

G01 X125．Y-#6 Z-#10 F100;

G01 Y-125．F1000;

#2=#10+0．2;(深度变量增加)

IF［#2NE40．6］GO TO 200;(深度控制语句)

G00 Z100．;(抬刀)

#1=#1+360/4;(角度累加)

G68 X0．Y0．R#1;(角度坐标旋转)

IF［#1NE360］GO TO 100;(角度控制语句)

G00 G40 G49 G80 Z100．;(取消循环，取消刀补)

M30;(程序结束并返回起点)

4 结语

在对斜度进行铣削加工的过程中，通常采用从上

由式(8)知:F1(ψ1，θ1，αi)=0

式(7)，(9)，(16)，(19)

由式(12)(13)(17)(20)知:

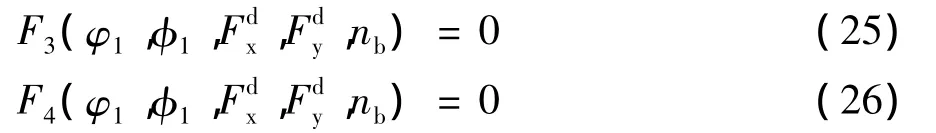
由式(15)～(17)知:

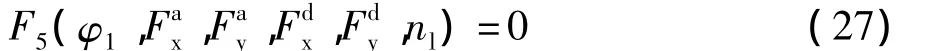
由式(2)、(10)、(18)、(19)、(20)知:

式(23)～(28)可知，这六个方程里共含有10个未知数，其中na，nb等四个是整数，可根据系统几何参数确定几组可能的数据，总有一组可满足上述六个非线性方程。另外六个未知数可通过联立六个方程求解。这样就解决了链传动系统的静态平衡问题。

4 算例

用拟牛顿法求解这一模型。参数设定如下:

D=350，R=80，L=80，Fg=3。得到图形如图 5所示。

由图5看出，用拟牛顿法能很好的求解这一模型。在此模型的基础上，可建立链轮传动的动力模型。

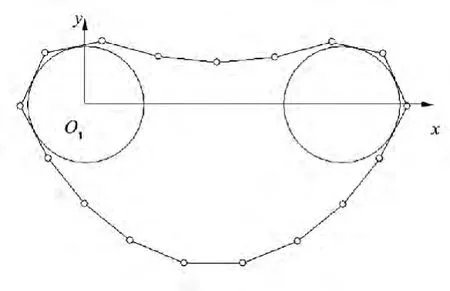
图5 模拟模型

5 结论

链传动系统一般有数目较多的链条和链轮组成，属于复杂的多刚体系统。由于刚体数目较多，系统的静力平衡状态不易计算和确定。而确定静力平衡状态是建立链传动动力学模型基本前提。将一节链条作为一个刚体处理，采用静力学的方法，解决链传动装置静平衡问题，较真实的反映链传动装置的静平衡状态。利用拟牛顿法解非线性方程组的程序算法，对链条传动装置进行静力学仿真，具有较好的计算效率。

［1］ 洪嘉振．计算多体系统动力学［M］．北京:高等教育出版社，2002．

［2］ 杨秀芳，张 峰．链条传动的受力分析［J］．机械管理开发，2003(6):11-13．