插齿刀刃磨误差及修正
■西安煤矿机械有限公司 (陕西 710032)
李 瑞 张维林

目前内齿均由插齿机直接加工成形,插齿精度要求较高。插齿加工过程中由于刀具磨损或损伤,插齿刀经常需要刃磨。刀具刃磨后能否有效保持刀具固有参数及精度,对加工零件精度有非常大的影响。因此,分析研究刃磨角度对齿形误差的影响、适当修正齿形角,对提高插齿刀刃磨精度,保证加工质量具有重要意义。
1. 插齿刀刃磨
插齿刀本身是一个变齿厚渐开线齿轮,其后面是渐开线螺旋面。标准插齿刀顶刃前角γ=5°,顶刃后角α=6°,而侧刃前角各点是不相等的,顶刃处最大,越靠近齿根部其侧刃前角越小,侧刃后角约2°。插齿刀用钝或切削刃损伤后,把前刀面磨成圆锥面并保证γ=5°。所用砂轮半径小于圆锥面的曲率半径,并将砂轮轴调至合适角度,才能磨出准确的前刀面,然后用此刀具才能加工出准确的渐开线齿形。
2. 插齿刀刃磨引起的齿形误差分析
按照日常生产习惯插齿刀一般只刃磨前角,所以这里主要研究前角刃磨引起的齿形误差。根据插齿刀设计原理,γ>0°前刀面为圆锥面,与齿形表面(渐开螺旋面)的交线(切削刃)在基面中的投影已不是渐开线。如图1所示,如以Ⅱ—Ⅱ截面中的渐开线齿形为基准,则齿顶在Ⅰ—Ⅰ截面中,齿顶厚度增大Δfa,同理齿根处厚度减薄Δff,相当于分圆压力角减小,造成较大的齿形误差。
如图2所示,通过插齿刀前刀面的锥顶作端截面O―O,得渐开线CD,以O―O为极坐标平面(基面),令坐标轴O0Y通过渐开线起点C,得渐开线的极坐标方程为
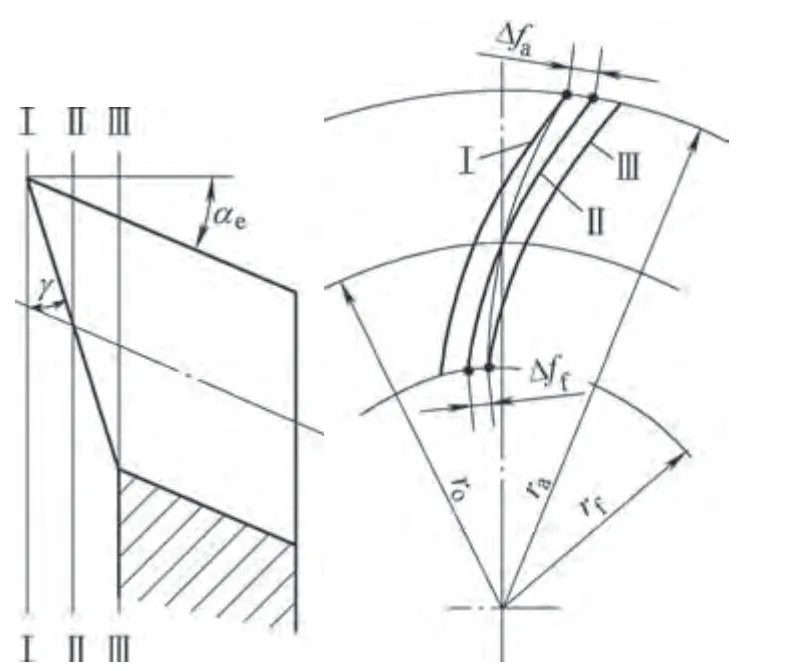
图1 刃磨前角引起的齿形误差
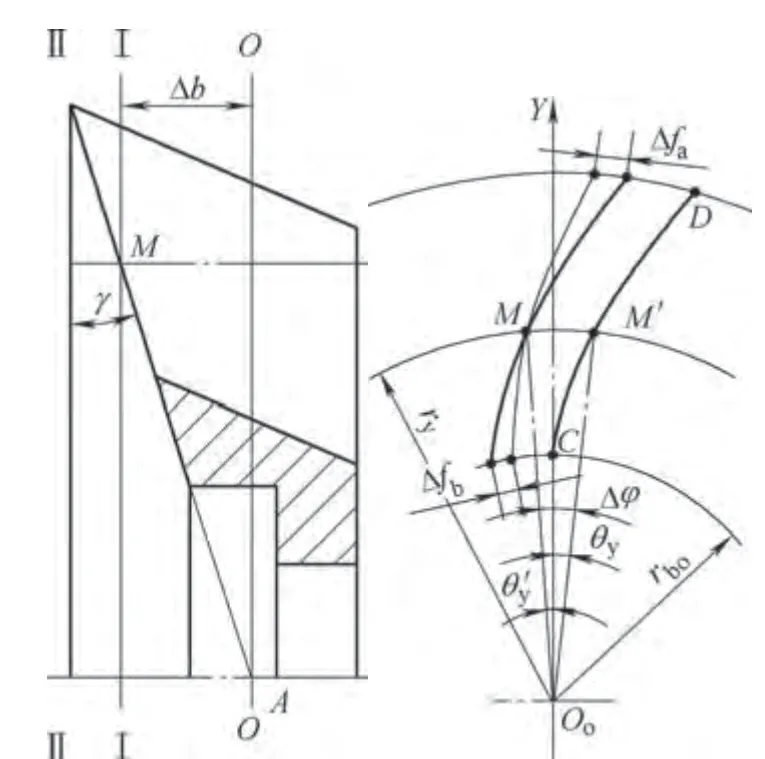
图2 插齿刀齿形误差分析

式中,αy=arccos(rbo/ry)。
对于切削刃上任意点M,该点的半径为ry,截面为Ⅰ—Ⅰ,离基面O-O 的距离为Δ b,则Δb=rytanγ。M点相对于M´点转过了Δϕ,其值为
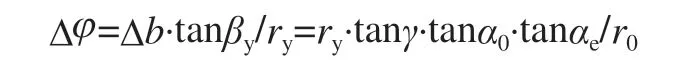
则可推出切削刃上任意点M的极坐标方程
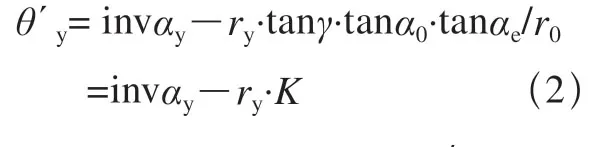
式中,K=tanγ·tanα0·tanαe/r0。
即为切削刃在基面上投影的方程式。如果插齿刀齿形表面的端面齿形角α0磨制成和齿轮分圆压力角相同,则切削刃在端面的投影将和理论渐开线有较大的误差。
3. 插齿刀齿形误差计算
如图3所示,AB是理论渐开线,它的分圆压力角为α,基圆半径为rb,CD为插齿刀切削刃的投影,插齿刀齿形表面的断面分圆压力角为α0,基圆半径为rb0,为便于比较切削刃投影和理论渐开线误差,将切削刃投影绕O0点旋转ε,使两线在分圆处重合,这时距离FB即为插齿刀顶圆处的齿形误差,AE为基圆处的齿形误差。切削刃投影曲线转过ε在分圆处αyε=α0,ry= r0。按照以上结论可得切削刃投影G´点角坐标θ´y0=invα0―r0·K,理论渐开线G点的角坐标θ=invα。切削刃旋转角ε=(invα0―invα)―r0·K,切削刃投影转过ε角后方程为θ″y0=θ´y0-ε。故切削刃投影和理论渐开线差值(以弧度计)可表示为:
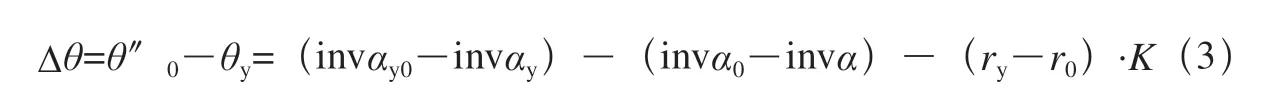
按圆弧长计可表示为Δfy=ry·Δθy,即在齿顶圆圆周方向的差值为Δfa= ra·Δθy,基圆处差值为Δfb= rb·Δθy。
实例计算插齿刀齿形表面的齿形误差。预定插齿刀参数:α=20°,m=5,z0=20,ha=1,ra=57.05,γ=5°,α=6°。插齿刀齿形角未修正,故α0=α,rb0=rb,αy0=αy。
计算可得该插齿刀顶圆和基圆处的齿形误差Δfa=―ra(ra―r0)·K =―0.026 9mm,Δfb=―rb(rb―r0)·K=+0.009 4mm。对插齿刀来说这样大的齿形误差是不允许的。而且插齿刀前角愈大齿形误差也愈大。
4. 齿形误差的修正
为减少刃磨前角带来的齿形误差,我们采用修正插齿刀齿形角的办法,即修正齿形表面的端面齿形角,使插齿刀的齿形角和齿轮分圆压力角不等。具体机理就是使刀具切削刃投影在分圆处的切线和理论渐开线的切线重合,这样导出刀具齿面的原始齿形角。
如图4所示,M是切削刃曲线上的任意点。根据微积分几何,M点的切线和向径之间的夹角Ψ为tanΨ= ry(dθ´y/dry),根据微积分原理和上述推导结论可得:
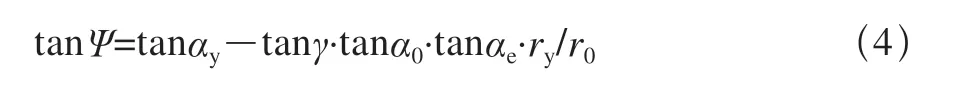
令在分圆处切削刃投影曲线的Ψ角等于理论渐开线的压力角α,则Ψ=α,αy=α0,ry=r0。即可得到tanα0=tanα/(1―tanγ·tanαe)。方程式为插齿刀齿形表面齿形角的修正值α0,修正后切削刃投影的分圆压力角正好是α,符合加工齿轮要求,但齿顶和齿根处仍有微量误差。
仍以前面插齿刀为例(α=20°,m=5,z0=20,γ=5°,α=6°),修正后的插齿刀齿形角为α0=2 0°1 0′1 4.5″,修正后的基圆
rb0=46.933 45mm,cosα0=0.822 67,cosαe=0.82 57,cosαb0=0.998 91,K= 0.000 067 556。故可计算出顶圆处的齿形误差Δfa=―0.006 92mm,基圆处的齿形误差Δfb=―0.007 565mm。
从计算结果可以看出,插齿刀齿形角未修正前顶圆和基圆处的齿形误差Δfa=―0.026 9mm,Δfb=+0.009 4mm;修正后齿形误差显著减少,Δfa=―0.006 92mm,Δfb=―0.007 56mm。
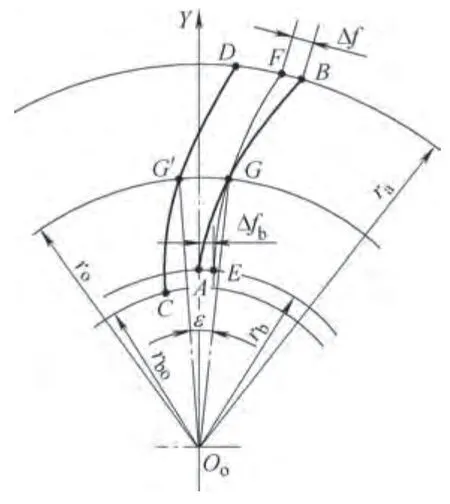
图3 插齿刀齿形误差计算
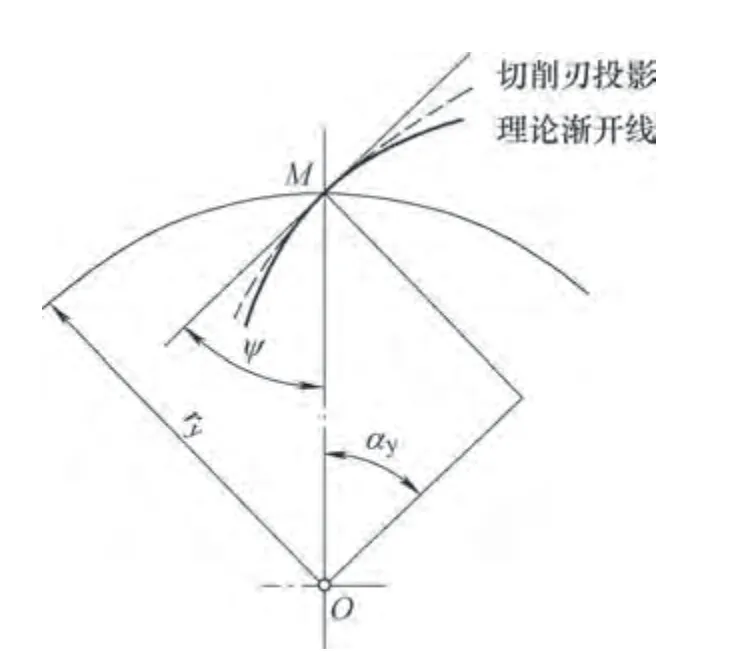
图4 插齿刀齿形角修正
从图5可以看出,修正后的切削刃投影在齿顶和齿根处比理论渐开线稍为凸出,这使得齿轮的齿廓有微量的顶切和根切,起自然修缘作用,可使齿轮啮合时减少干涉和噪声,因此插齿刀的微量齿形误差还是允许的。尤其对于新旧插齿刀正负变位量绝对值相差不大或变位量不大的插齿刀更为适宜,因为这样修正后使齿顶和齿根的齿形误差大致相等,插齿刀加工出的齿轮具有较高的齿形精度。
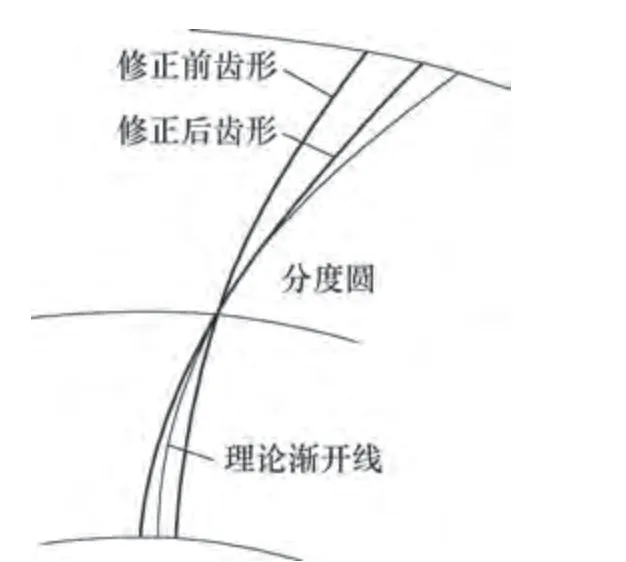
图5 修正前后刀刃投影和理论渐开线比较
[1] 袁哲俊,等. 齿轮刀具设计[M].北京:新时代出版社,1983.
[2] 谢明,钦柯,等. 齿轮刀具[M].北京:机械工业出版社,1965.

