人形机器脚设计仿真

王梦婕

（西南交通大学峨眉校区 四川峨眉 614200）

人形机器脚设计仿真

王梦婕

（西南交通大学峨眉校区 四川峨眉 614200）

人形机器人一直是机器人研究领域的热点，它集中了机械电子工程、计算机工程、信息工程、自动控制工程以及人工智能和仿生学等多种学科.而中间最重要的是机器脚的设计，它关系到机器人的稳定性，若不稳定则不能达到我们预期的效果，而在运动过程中，步行步态的研究又至关重要，故在前人的基础上，将继续研究设计机器脚的行走的步行步态，以及确定该机构的尺寸结构。

行走步态 杆长确定 运动仿真

一、具体设计要求：

可按一般人高度的一定比例确定其原始参数，如腿高、步幅等，确定整个机构各个杆件的具体尺寸和运动副类型；

二、机构分析

2.1 机构自由度计算

如机构简图所示，该机构具有六个活动件（BC EH BCE ADF GIJ FHG），具有八个平面低副，无高副，故自由度如下：

由上式可知，该机构具有两个自由度，若要使运动单一且确定，故主动件应需要两个，则经分析知，AB为机架，BC为主动件，以及需要在铰G处装一个电机，驱动GIJ的运动。

2.2 机构分析

在此机构中，ADF、CDE、FHG、IGJ构成桁架，因此固定不动。在机构运动过程中，模拟脚踝和膝盖处的运动是关键的，IGJ作为桁架只需要研究G和模拟膝盖为F点，故只需要研究G、F两点。

在桁架FHG中，G的运动可由H、F两点来确定，而F、H的运动又由A-D-C-E-H-F这一各部分确定，又因为ADF、DCE是两个桁架，则F、H的运动分析可以简化为D-E-F-H这一四杆机构运动的分析。同理，A-B-C-D也可近似地认为是一个四杆机构，且AB为机架。并且在分析过程中，从下至上依次分析，即先分析D-E-F-H，随即分析A-B-C-D。当分析D-E-F-H时，将杆DE看做机架，并且此四杆机构应为双摇杆机构。

所以，这个机构的运动分析就简化为了两个四杆机构的组合。

三、走形方案与步态规划

1.与步态规划有关的概念

步长：在一个步行周期内，摆动腿所移动的距离。

步行周期：摆动腿完成一步所经历的时间。包括一个单脚支撑期和一个双脚支撑期。

单脚支撑期：在一个步行周期中，由一只脚对机器人进行支撑所经历的时间。

双脚支撑期：在一个步行周期中，由两只脚同时对机器人进行支撑所经历的时间。

一个完整的步行过程应该包括起步、加速、稳定步行、减速、停止五个阶段。周期性运动包括左腿步行周期和右腿步行周期，而两个步行周期完全对称，时间上相差了一个步行周期，因此只需要研究一个步行周期，当步行机器人行走较为缓慢的时候，则完整的步行过程可以近似看作只包含起步、周期性运动、停止三个步行过程。

2.步态规划

起动阶段，机器人的重心高度将由初始位置降低到合适行走的高度，同时重心在地面上的投影从两腿中心位置移动到支撑腿上。通过机构运动向前迈出半步，重心返回两腿之间的中心位置。机器人就由直立的静止状态过渡到了稳定步行阶段。

稳定步行阶段，双脚交替向前迈出，重心在两脚中间不断转换，始终保持在支撑腿平面内。设向前迈步的步长为一个脚底的长度。

停止阶段，先在重心在地面上的投影从两腿之间的中心位置移动到支撑脚上的同时，是机器后腿向前跨出半步，与支撑脚齐平。再移动机器人重心到两腿之间的中心位置同时升高重心恢复到初始位置。

3.主要参数的设定与条件假设

模拟大腿（即AF）长：480mm.

模拟小腿（即FG）长：430mm.

桁架CDE为等边三角形.

因为在行走过程中脚抬得越高避障能力增强，但是稳定性降低，不要求进行避障，故行走时抬脚高度为：15mm.

在行走过程中，完成一步的时间为：6s.

在此课题研究下，只研究稳定步行阶段.

在行走过程中，脚底始终与地面保持平行。

4.主要构件的运动轨迹分析与确定

已知可将整个机构化简为两个四杆机构的运动，故各关键点的运动轨迹应为两个四杆机构运动的叠加。可以对每个四杆机构中的各点在完成一步最后假设其位置。（叠加是指两个四杆机构分别独立运动互不干扰，即四连杆D-E-F-G运动时，将DE看作是机架。四连杆A-B-C-D运动时，AB为机架，然后进行叠加）

四连杆D-E-F-H的轨迹运动分析

四连杆D-E-F-H应为双摇杆，故最长杆与最短杆长度之和应当大于其余两杆长度之和。即：

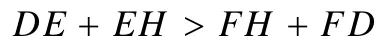
桁架ADF在整体运动时绕A点做圆周运动，故F点速度方向垂直于AF.

四连杆A-B-C-D的轨迹运动分析

四连杆A-B-C-D为曲柄摇杆机构，其中AB为机架，BC为曲柄，AD为摇杆。假设AB为最长杆，则：

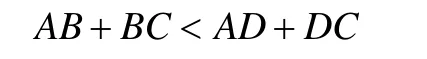
在整体机构的运动中，点F应该绕A点做圆周运动。

5.机构运动尺寸综合计算

5.1 尺寸综合

因该机构如果完全使用解析法计算，不确定因素太多，七杆机构的计算太过复杂，所以在此我想先假设AB、BC、CD、AD四杆的长度，然后根据其他条件计算剩余杆长，确定具体运动。

假设AB=150mm，BC=80mm，CD=120mm，AD=160mm.如下图所示，是摆杆AD的摆角

在三角形ABD’中，AB=150，BD’=40，AD’=160，由余弦定理知

在三角形D’AD’’中，D’D’’=174.3mm.

在三角形ABD’中，由余弦定理得：