笛卡尔色彩空间的美术设计规则

罗兆麟，王 利

（1.沈阳师范大学学前与初等教育学院，辽宁沈阳110034；2.沈阳师范大学软件学院，辽宁沈阳110034）

笛卡尔色彩空间的美术设计规则

罗兆麟1，王 利2

（1.沈阳师范大学学前与初等教育学院，辽宁沈阳110034；2.沈阳师范大学软件学院，辽宁沈阳110034）

依据三原色定理，建立以三原色为基底的笛卡尔色彩空间。该空间中的每个点为特征色彩的代表点，代表点在空间位置的变化给出了一切美术设计所需色彩的完备集。考虑人类视觉的有限性和局域性，对艺术鉴赏的独特性和趋同性，感光效果的相似性和认同性，在笛卡尔色彩空间中（R，G，B）运用映射技术，给出了美术设计的若干新思路和新规则。

三原色；笛卡尔色彩空间；美术设计

三原色原理是任何颜色都可以用“红（red）”“绿（green）”“蓝（blue）”三种颜色按照不同的比例混合而成，反过来每种颜色都可以分解为含有不同比例的这三种基本颜色，三原色之间是相互独立存在的，是由三种基本“原色”构成（原色是指不能用其它色混合调配而成的“基本色”），因此，用几何学的术语来说，三原色彼此正交。以不同比例将诸原色混合，可以产生出其他的新颜色。色彩学上将这三个独立的颜色称为三原色，红、绿、蓝即是三原色，这三种颜色合成的新颜色范围最为广泛。独立、正交、不同比例叠加给出新数据，使我们不难联想到笛卡尔坐标系，建立以三原色为基底的笛卡尔色彩空间就变得水到渠成了！进一步以数学的向量空间来解释整个色彩系统，则三原色在色彩空间中可作为一组基底向量（r，g，b）的完备集，并且由此能组合出一个“色彩空间”的全景描绘。

一、以三原色为基底的笛卡尔色彩空间的构建

色彩空间，即色域（Color Space），也可以称为色彩模型。实际上就是各种彩色的集合范围，它代表了色彩影像所能表现的色彩具体情况。色彩的种类越多，色彩空间就越大，能够表现的色彩范围也就越大。通常人们按照一定的规律把这些色彩整合起来，建立起多种类型的色彩模型，如一维、二维、三维、甚至四维空间坐标来规范表示这些色彩，系统化的色彩空间就是某种坐标系统所能定义的色彩范围［1］。进一步地说，它是一系列颜色的数学表现形式，这种数学表现形式可以更直观地通过笛卡尔三维坐标系来直接表达。在构建笛卡尔三维色彩空间前，我们有必要熟悉一下二维直角坐标系，即通常用X轴和Y轴及两个坐标轴的相交点（称为原点）来表达，这个原点通常被标记为0。两个不同的坐标轴分别指向各自特定的方向且彼此垂直，这些特定方向决定了一个平面，我们称为“XY平面”，又可称之为“笛卡尔平面”。通常习惯将X轴水平摆放，称为横轴，指向右方；Y轴被竖直摆放，称为纵轴，通常指向上方。三维笛卡尔坐标（X，Y，Z）与二维笛卡尔坐标（X，Y）相似，区别于在X轴和Y轴的基础上又增加了Z轴并且垂直于“XY平面”，三轴彼此正交、有共同的原点O。如图1所示：

图1 笛卡尔三维空间坐标系

所谓笛卡尔色彩空间，就是以三原色为基底的笛卡尔系统所描述的空间，这种空间也是绝对空间。所谓绝对，就是这种空间不受外物的影响，始终保持自身静止、恒定不变的特性，并且所有物体都占据着这个空间，这里的物体包含着很多元素。如三原色中的（红、黄、蓝），笛卡尔坐标中的（X，Y，Z），代表任意时间的t等等。所有“元素”的运用都是在这个绝对静止的参照系中发生，它是连续的、无限延伸的、具有三维或多维的，它也是均匀的、各向同性的，并且所有的坐标点都是相互等价、相互联系的。说它是各向同性的，即表明通过同一个点的所有直线或曲线相互连接，并且等价。空间和时间是一样的，也是绝对的，我们可以把空间内部看成是一组或多组点的集合，每个点都有各自的坐标，并且这个坐标是空间中的最小元素，而不再有其内在的机构，是永久存在的，它可以被另一个“物体”所占据，这个所谓的物体可以是三原色中的色谱、三维笛卡尔坐标中的（X，Y，Z）、三全音中的音符以及时间的坐标“t”等等。空间中的点被这些其他符号或色彩元素所替代，这种替代可以上下左右无限连续地排列或组合，可以充分体现空间具有连续性和无限性，当某个物体或原色占据了空间中的某个笛卡尔坐标领域，为了避免元素之间互相排斥，那么其他元素将不会再次占据这个坐标［2］。周围几个坐标中的元素，可根据其特性展现自己的特征，也可组合成独特的特性。每个坐标组可同时存在不同类型的元素，发挥其各自功效。当这个元素或物体被拿开，那么这个坐标点的空间可变为空的坐标点，其他元素可再次将其空间占据［3］。

二、笛卡尔色彩空间中的点、线、面、体含义诠释

平时我们经常用到的色彩空间主要有RGB、CMYK、Lab等，而RGB色彩空间更常用，它是通过红、绿、蓝三原色来描述颜色的颜色空间。在色彩空间中有256种颜色，一个像素值的（红、绿、蓝）成分分别为（255，0，0）时显示为红色、为（0，255，0）时显示为绿色、为（0，0，25）时显示为蓝色。自然界中所有的颜色都可以由红、绿、蓝这三种颜色合成，数字图像也是如此，可用坐标轴表示，如R轴领域代表红色区域，G轴领域代表绿色区域，B轴领域代表蓝色区域。针对红、绿、蓝分量的多少，人为地划分为0-255共256个等级，0表示不含有红、绿、蓝的成分，255表示含有100%的红、绿、蓝成分，根据红、绿、蓝各种不同的成分搭配组合就能表示出各种颜色。把色彩看成连续变化时，即可建立一个连续变化的笛卡尔色彩空间。其中的三原色（红、绿、蓝）可设定为（R，G，B）三个坐标轴。如图2所示：其中每个轴的单位长度作为基底向量（r，g，b），它们是完备的，能够给出一个“色彩空间”的全景描绘。

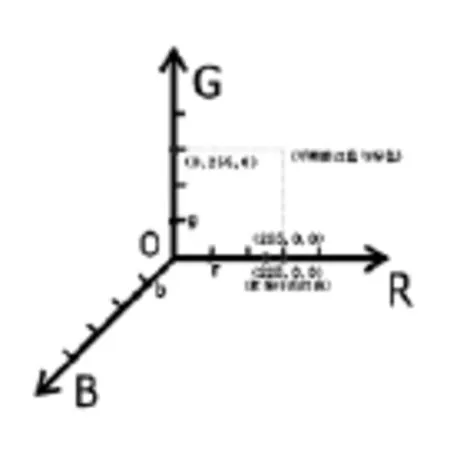
图2 笛卡尔彩色空间坐标系

不同空间的景象是完全不同的，相互映射的结果会给出出乎想象的、非常美妙的绘景。比如在坐标空间（X，Y，Z）中的一条红领巾，它是红色的并且有几何形状，而RGB的数值分别为255，0，0。在笛卡尔色彩空间中（R，G，B）的显示就是红色光轴R上的一个点；又如带有五角星的绿色军帽是由红色和绿色组成，并且有几何形状。红色的RGB的数值分别为255，0，0，绿色的为0，255，0，复合表示为255，255，0。在笛卡尔色彩空间中（R，G，B）的显示就是红色光轴R上的一个点和绿色光轴G上的一个点。这些和实际的景物完全不是一回事，但在（R，G，B）中定量地处理问题时却被大大地简化了，这就是提出笛卡尔色彩空间的意义所在！依据三原色定理，我们选定以三原色为基底的笛卡尔色彩空间中的任意点为特征色彩的代表点，那么代表点在空间中位置的变化给出了一切美术设计所需的色彩，代表点位置变化所留下的一条曲线，即是色彩变化的一个过程。代表点在空间中位置的密集变化可留下一个曲面或一个体积，这个曲面或体积可代表一个复杂色彩体系的色彩复杂变化过程。如一个人骑着一匹马在草原上奔跑，人物、马、草原等所呈现的颜色是一复杂色彩体系，颜色的跳动性也比较大，但是在（R，G，B）中，运用色彩的数字坐标值可轻松表达，在某一时刻所展现的某一具体颜色组群，通过轨迹的连接，形成一个曲面以表达在某一特定局域时间段内的色彩变化。

三、美术设计新规则思考

艺术美学是设计美学的基础，想象是形象思维的基础，模仿只能造出我们已经见过的东西，但想象却能创造出没有出现过的东西。我们应该促进设计的发展，形成设计艺术的取向，体现设计的价值和美感［4］。通常我们总强调设计与艺术的结合、艺术的形象思维与设计的理性思维的结合，其实，所有的设计原理、设计方法、设计理念都是设计思维的知识储备，都会在设计思维中发挥潜在的效能。鉴于此，我们考虑人类视觉的有限性和局域性，对艺术鉴赏的独特性和趋同性，感光效果的相似性和认同性，在笛卡尔色彩空间中（R，G，B），运用映射技术，给出美术设计的若干新思路、新规则：（1）光彩夺目题材的设计多在（R，G，B）轴线附近截取效果明显，强弱对应于不同轴线的不同点；（2）色彩简单平和题材的设计多表现在（R，G，B）空间中的平滑曲线；（3）场面宏大色彩丰富题材的设计多表现在（R，G，B）空间中的高次曲面；（4）有艺术价值的题材共性致使（R，G，B）空间的有效部分收缩成一个较小的区域；（5）通常意义下有艺术价值的题材设计多表现为（R，G，B）空间中的点、线、面结构，而很少有凝聚成实心体积的。

进一步开发我们的想象空间，在艺术设计中如果把一些符号如三原色（红、绿、蓝）、三维笛卡尔坐标中的（X，Y，Z）、三全音中的音符、以及时间的坐标t等等放在一个空间中，那么就推出了十维空间坐标概念，即10D空间。在这个空间中，一个点就代表某一时刻局域视觉和听觉的整体感受；一条曲线则代表某一特定时间段内局域视觉和听觉的整体感受的变化；一个曲面则代表某一特定局域时间段内全景视觉和听觉的变化，即视觉与听觉的完美结合体系随时间的变化而变化的过程。

［1］周至禹.思维与设计［M］.北京：北京大学出版社，2007：11-13.

［2］童强.空间哲学［M］.北京：北京大学出版社，2011：25-27.

［3］李洲圣，唐长红.三维空间张量分析的矩阵方法［M］.北京：航空工业出版社，2010：47-50.

［4］尼尔·伦纳德，安布罗斯.创新设计思维［M］.北京：中国青年出版社，2014：27-29.

【责任编辑王凤娥】

J0-03

A

1674-5450（2015）05-0191-02

2015-07-11

罗兆麟，女，辽宁沈阳人，沈阳师范大学讲师；王利，男，辽宁辽阳人，沈阳师范大学讲师，工学博士。