海底裸置与埋置管线自沉过程对比研究

唐丕鑫，杨树耕，宋艾恒，刘晓峰，徐 蒙，王 晗

(1.天津大学 水利工程仿真与安全国家重点实验室，天津 300072;2.上海外高桥造船海洋工程有限公司，上海 200306)

海底管线是海洋油气输运系统的重要组成成分，在海底复杂环境作用下，容易产生大变形而失稳。一旦失稳，由于管线结构破损，将会引起管内油气泄漏，造成巨大的经济损失与环境污染，因此必须以管线稳定性为核心进行设计、安装与维护。海底管线铺设方式分为裸置与埋置两种，不论采取何种方式，管线铺设后都会在其自身与配载重力作用下逐渐嵌入海床土体，最终达到管土平衡状态。

裸置管线方面，Mei 等运用边界层理论以多孔弹性模型为对象研究波浪、管线、土体三者耦合作用问题;Jeng 等［1］运用有限单元法研究管线下方土体响应问题;任艳荣等［2］运用ABAQUS 研究海底管线在砂质海床条件下稳定性问题。埋置管线方面，Lai 等［3］运用有限差分法和有限单元法研究管线在可渗刚性海床下所受的波浪力;MacPherson［4］研究了无限深海床下管线所受波浪力的解析解;白玉川等［5］研究了管线与沙质海床间的相互作用。在以上研究的基础上，以南海深海区为研究背景，对裸置和埋置管线自沉过程进行数值模拟计算，并进行相应数据的比较分析，从而为实际应用提供参考。

1 参数的选取与设置

1.1 本构关系

ABAQUS 中可以根据研究内容不同选取不同的本构关系，根据本文管土作用特点，依照计算结果准确可信，计算模型相对简化的原则，采用Mohr-Coulomb 模型作为海床土体本构关系进行建模计算。

1.2 管土接触作用

在裸置与埋置管线自沉过程中，管线与海床土体经历分离-接触-结合的过程，在ABAQUS 计算中，需要设置接触对模拟接触过程。本文采用典型的主-从接触算法［6］，主从面的选取需遵循以下原则:1)从面应是网格划分更精密的表面;2)若两者网格密度相近，从面应是较柔软材料构成的表面。因此在裸置管线计算中，将管线下半部分作为主面，海床土体取长度为4 个管径长度的表面作为从面;在埋置管线计算中，将管线外表面设置为主面，与管线外表面相接触的土体表面设置为从面。

1.3 海床土体长度与高度选取

管土相互作用研究中土体长度与高度的选取十分关键，既要排除边界效应对数值模拟结果的影响，又要使模型尽量简化，计算时间较短。参考已有的研究成果，选取管径为0.5 m，土体长度分别为20 倍管径、30倍管径、40 倍管径，土体高度分别为10 倍管径、20 倍管径、30 倍管径进行比较，建立有限元模型如图1 和图2 所示，计算相同管径下的土体沉降量(见表1 和表2)。

图1 土体长度不同的有限元模型Fig.1 The finite element model of different soil length

图2 土体高度不同的有限元模型Fig.2 The finite element model of different soil height

表1 不同土体长度下的土体沉降量Tab.1 Soil settlement under different soil lengths

表2 不同土体高度下的土体沉降量Tab.2 Soil settlement under different soil heights

由表1 和表2 可知，土体在不同长度和高度下的沉降量变化均在10－4m 数量级，变化率均小于1%，因此遵循计算结果准确且计算量又较小的原则，在建立有限元模型时，海床土体长度取为20 倍管径，土体高度取为10 倍管径。

2 有限元模型

海底管线自沉模型由管线与海床两部分构成，均采用连续的三维实体单元。管线模型长5 m，直径0.5 m，壁厚0.1 m，裸置管线置于海床上表面，由于研究以南海深海为背景，海底环境复杂多变，管线埋置越深施工作业难度越大，因此设置埋置管线轴线与土体上表面距离为1 m，管线参数如表3 所示;海床土体模型长10 m、宽5 m、高5 m，土体采用已知南海深海区原位的粉质砂土，参数如表4 所示。在网格划分时，管线与土体均采用八节点六面体线性减缩积分单元(C3D8R8)，并对管土接触处进行局部细化，建立裸置与埋置管线有限元模型(见图3)。

表3 管线模型参数设置Tab.3 Details of the pipeline model

表4 海床土体模型参数设置Tab.4 Details of the seabed soil model

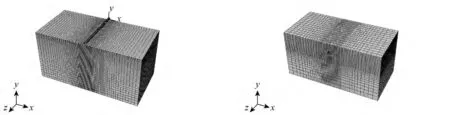
图3 裸置与埋置管线有限元模型Fig.3 The finite element model of bare and buried submarine pipeline

在海床土体侧面限制X 向、Z 向位移，施加约束S1=S3=0，不约束S2(竖直方向Y 的位移)，在海床底面施加全约束S1=S2=S3=0;海床上表面作为自由表面，允许自由排水，孔隙水压力为0。由于本文模拟的为南海深海海底环境，参考已有现场数据与研究成果，在水深较深的海底波流力对管线的影响较小，因此忽略管线在自沉过程中所受到的波浪力、海流力。同时以管线铺设后尚未运行阶段为背景，管线所受载荷主要包括管线及配载重量、浮力，不包括内部所运输油气的重量。管线及配载重量以改变管线密度的形式施加，浮力沿Y 轴正向以均布载荷形式施加。

3 计算结果与分析

3.1 初始地应力平衡

在管线自沉过程研究中，海床土体的初始地应力是必须予以考虑的问题，直接影响计算结果的准确性。依照初始应力场的施加必须满足平衡条件和屈服条件的原则，结合本文土体结构形状较规则的特点，采用的施加方法为［7］:给出土体最高点、最低点的自重应力值和对应坐标，通过ABAQUS 自行运算，从而得到同时满足平衡条件和屈服条件的等效初始地应力场。初始地应力平衡后的土体竖直位移分布如图4 所示，Mises应力分布如图5 所示。

图4 地应力平衡后土体竖直位移分布Fig.4 Soil vertical displacement distribution under the balanced in-situ stress

图5 地应力平衡后土体竖直方向Mises 应力分布Fig.5 Soil vertical Mises stress distribution under the balanced in-situ stress

由图4 和图5 可知，在平衡地应力后土体竖直位移排列有序，为10－10m 的数量级，Mises 应力由上至下依次递增，形成了一个既满足平衡条件又不违背屈服准则的初始地应力场，可使计算结果更加准确。

3.2 自重载荷下的计算结果

在平衡土体初始地应力后，进行管土接触、管线及配载重量、浮力施加、海床土体固结分析，约束条件保持不变，计算得到裸置管线和埋置管线土体竖直位移变化(见图6)，管线竖直位移变化(见图7)。

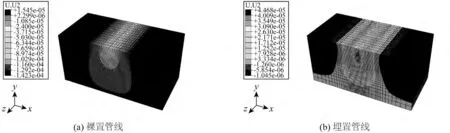
图6 自重载荷下裸置与埋置管线土体竖直位移分布Fig.6 Soil vertical displacement under the bare and buried pipeline gravities

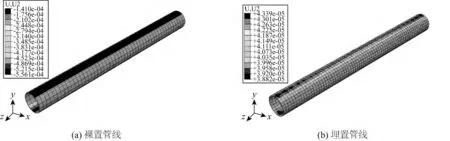
图7 自重载荷下裸置与埋置管线竖直位移分布Fig.7 Pipeline vertical displacement under the bare and buried pipeline gravity

由图6 可知，裸置与埋置管线施加自重载荷及浮力后，在海床土体上形成了以管土接触处为中心的水滴状影响区域。裸置管线土体竖直位移呈现中心向下，两端向上的“沉降”效应，最大沉降量出现在管线与土体接触处，为1.42 ×10－4m，并且形成由内向外依次递减的趋势;埋置管线由于管线平均密度小于周围土体密度，且管线埋深较浅，管线上方土体重量不大，致使两侧土体向中心管线处挤压，使管线抬升，土体竖直位移呈现中心向上，两端向下的隆起效应，最大位移出现在管线与土体接触最上端，为4.47 ×10－5m，亦呈现由内向外依次递减的趋势。同时可以发现，由于裸置与埋置管线尺寸与土体相比较小，因此其对土体形成的影响也较小，土体竖直位移均小于10－3m 数量级。

由图7 可知，裸置与埋置管线竖直位移均随土体的变化趋势而变化，形成沉降与隆起效应，竖直方向最大弯曲量均位于管线最上端，分别为5.56 ×10－4m、4.34 ×10－4m，量级均在毫米级，与管线的尺寸量级相近，对管线的稳定性影响较大。

4 参数变化的影响与分析

4.1 管线重量变化的影响

保持裸置与埋置管线外径不变，通过改变壁厚的方式改变管线重量，其余参数设置均保持不变，得到土体竖直位移随管线壁厚的变化(见图8)。由图8 分析可知，同一管线重量下的裸置管线土体竖直位移绝对值均大于埋置管线，裸置管线土体竖直位移向下，形成沉降趋势，沉降量为10－4m 数量级，且随管线重量增大而成线性增大关系，表明此时土体应力未达到屈服极限，土体发生弹性变形，若管线重量继续增加，将会使一部分土体达到弹性屈服极限，进入塑性状态，而使土体沉降量显著增大。埋置管线土体竖直位移向上，形成隆起趋势，隆起量为10－5m 数量级，且随管线重量增加而成线性减小关系，表明管线重量越大，管线平均密度越接近土体密度，两侧土体挤压效应越小，土体隆起量亦越小。

4.2 管线外径变化的影响

保持裸置与埋置管线重量不变(即壁厚不变)，改变管线的外径大小，其余参数设置均不变，分别计算裸置与埋置管线在壁厚为10 mm 和20 mm 下的土体竖直位移，得到土体竖直位移随管线外径的变化(见图9)。由图9 分析可知，同一管线外径下的裸置管线土体竖直位移绝对值均大于埋置管线。裸置管线土体竖直位移向下，且随管线外径的增大呈线性增大关系，表明此时土体应力未达到屈服极限，产生的变形为弹性变形;管线重量越大，土体竖直位移随外径变化的线性增长速率越大。

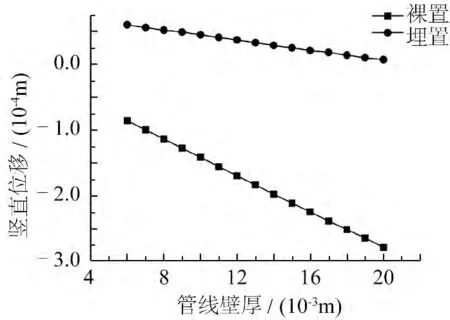
图8 土体竖直位移随管线壁厚变化Fig.8 Effect of pipeline thickness on soil vertical displacement

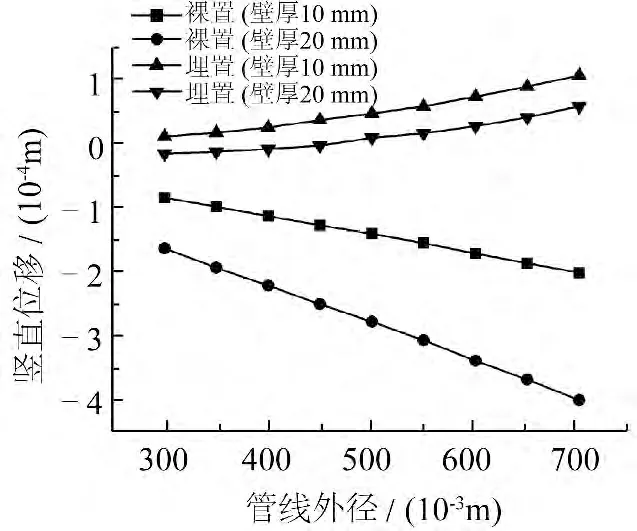
图9 土体竖直位移随管线外径变化Fig.9 Effect of pipeline diameter on soil vertical displacement

埋置管线计算中，壁厚为10 mm 的埋置管线土体竖直位移向上，壁厚为20 mm 的埋置管线土体竖直位移方向经历由下至上的变化过程。表明当管线重量较大，外径较小时，管线的平均密度大于土体密度，管线两侧土体向中心挤压效应消失，从而形成中心沉降趋势。由于管线平均密度略大于土体密度，所以形成的沉降量较小，为10－5m 数量级。随着管线外径的不断增大，管线的平均密度逐渐减小，管线两侧土体向中心挤压效应逐渐明显，土体竖直位移逐渐由沉降过渡为隆起的趋势，隆起量随管线外径的增大而增大，但数值均较小，为10－5m 数量级。同时随着管线外径的不断增大，管线对土体作用的影响区域也在不断扩大，因此在建立管土接触模型时，土体长度的选取尤为关键，一定要长于管线影响区域的边界，否则边界效应将使计算结果和实际数据相差较大，不具可信性。

4.3 土体杨氏模量变化影响

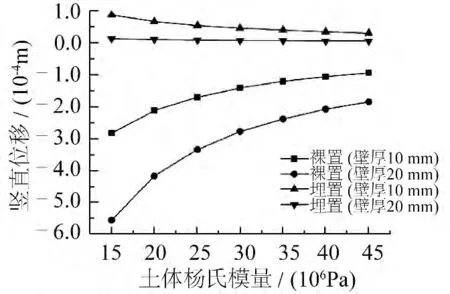
图10 土体竖直位移随土体杨氏模量变化Fig.10 Effect of soil Young＇s Modulus on soil vertical displacement

改变土体的杨氏模量，其余参数设置均保持不变，分别计算裸置与埋置管线在壁厚为10 mm 和20 mm下的土体竖直位移，得到土体竖直位移随土体杨氏模量的变化(见图10)。由图10 可知，同一土体杨氏模量下的裸置管线土体竖直位移绝对值均大于埋置管线。裸置管线土体竖直位移向下，埋置管线土体竖直位移向上，且均随土体杨氏模量的增大而减小。当杨氏模量较小时，土体竖直位移随杨氏模量的变化幅度较大;杨氏模量逐步增大时，土体竖直位移随杨氏模量的变化幅度逐步平缓。分析可知，土体杨氏模量较小时，土体刚度较小，易于发生变形;当土体杨氏模量逐步增大时，土体刚度逐步增大，土体所发生的弹性变形将逐步减小。

4.4 土体粘聚力变化影响

改变模型土体的粘聚力，其余参数设置均保持不变，分别计算裸置与埋置管线在壁厚为10 mm 和20 mm下的土体竖直位移，得到土体竖直位移随土体粘聚力的变化(见图11)。由图11 可知，同一土体粘聚力下的裸置管线土体竖直位移绝对值均大于埋置管线。裸置管线土体竖直位移向下，当土体粘聚力较小时，土体竖直位移较大，说明此时部分土体已达到弹性屈服极限，进入塑性状态，产生塑性大变形;当粘聚力不断增大时，土体竖直位移不断减小，说明进入塑性变形的土体越来越少，当粘聚力达到一定数值时，土体全部进入弹性变形状态，由于外压力为定值，土体竖直位移将不再改变，维持较小值的状态。埋置管线土体竖直位移向上，由于管线整体对下方土体压力不大，导致粘聚力的变化未使土体进入塑性状态，当其他条件未发生改变时，土体竖直位移将在弹性范围内保持不变。

图11 裸置与埋置管线土体竖直位移随土体粘聚力变化Fig.11 Effect of soil cohesion on soil vertical displacement of the bare and buried pipelines

5 悬跨管线研究

图12 管线悬跨示意Fig.12 Schematic diagram of pipeline span

已有勘探资料表明［8］，南海深海海底发育有大量的沙坡沙脊，且在海底复杂的环境作用下，进行无规则的迁移和推移运动。沙坡沙脊的运移易造成部分管线悬空，形成悬跨状态，悬跨长度也随着沙坡沙脊的运移在不断变化，这给管线的安全带来极大的风险。本文在以上研究的基础上，将裸置管线与土体宽度拉伸为10 m，通过在土体中设定生死单元的形式使管线形成悬跨状态(见图12)，其余参数设置均保持不变。分别计算管线壁厚为10 mm 和20 mm，悬跨区位于管线中心处，悬跨长度不断扩大时的土体和管线竖直位移，得到土体与管线竖直位移随悬跨长度的变化(见图13)。

图13 管线和土体竖直位移随悬跨长度变化Fig.13 Effect of span length on pipeline and soil vertical displacement

由图13 分析可知，同一悬跨长度下的管线竖直位移均大于土体竖直位移，且均随着悬跨长度的增加而增加，管线竖直位移最大值位于悬跨中心处最上端，土体竖直位移最大值位于管线悬空与未悬空的分界面与土体接触中心处。在悬跨长度较小时，管线与土体的竖直位移均较小，且与管线未悬空时的数值相接近，略有增长。当悬跨长度达到一定数值时，管线与土体竖直位移有大幅度增加，说明此时管线两端土体无法提供有效的支撑，土体被压溃，管线和土体同时产生较大变形，变形量与管径处于同一数量级，较为危险。因此在海底管线安装与维护过程中，一定要注意悬跨对管线造成的影响，当悬跨长度过大时及时采取有效措施降低悬跨长度，保证管线运营安全。

6 结 语

1)利用ABAQUS 软件对海底裸置与埋置管线自沉过程进行建模，通过平衡海床土体初始地应力，设置管土接触，进行管线的配载重量及浮力施加、海床土体固结分析，计算得到的管线和土体竖直位移与实际情况基本吻合，具有一定的实际应用价值。

2)裸置管线方面，研究发现:管线重量、外径，土体杨氏模量、粘聚力都对土体竖直位移有不同程度的影响，影响的大小程度取决于土体是否进入塑性屈服状态，参数的改变使土体更容易发生塑性屈服，土体的竖直位移量更大。

3)埋置管线方面，研究发现:当管线埋深较浅、管线上方土体重量不大的情况下，土体竖直位移与管线整体的平均密度有关。当管线平均密度小于周围土体密度时，两侧土体便向中心管线处挤压，使管线抬升，土体竖直位移呈现中心向上，两端向下的隆起效应;当管线平均密度大于周围土体密度时，两侧土体挤压效应消失，形成沉降效应。由于管线平均密度与周围土体密度相差较小，因此土体竖直位移量亦较小，只有当密度相差较大时，管线和土体竖直方向变形才更加明显。综上，当管线埋深较浅、管线上方土体重量不大的情况下，参数的改变使管线平均密度与周围土体密度相差越大、土体越容易发生塑性屈服，土体的竖直位移量越大。

4)管线悬跨研究中，当管线悬跨长度过大时，管线两端土体将无法提供有效的支撑，土体被压溃，管线易产生大变形而失稳。因此在海底管线安装与维护过程中，一定要注意悬跨对管线造成的影响，当悬跨长度过大时及时采取有效措施降低悬跨长度，保证管线运营安全。

［1］JENG D S，CHENG L.Wave-induced seabed response around a pipe laid on a poro-elastic seabed［J］.Journal of Offshore Mechanics and Arctic Engineering，1999，121:227-236.

［2］任艳荣，刘玉标，顾小芸.利用ABAQUS 软件分析砂质海底管线稳定性［J］.中国海洋平台，2001(5):68-72.(REN Yangrong，LIU Yubiao，GU Xiaoyun.The stability analysis of naked pipeline laying on a sandy seabed based on ABAQUS program［J］.Chinese Offshore Platform，2001(5):68-72.(in Chinese))

［3］LAI N W，DOMINGGUEZ R F.Numerical solution for determining wave-induced pressure distributions around buried pipelines［R］.USA:Tex A ＆ M Univ.，Dep.Civ.Eng.Rep.COE 182，1974.

［4］MACPHERSON H.Wave forces on pipeline buried in permeable seabed［J］.Journal of the Waterway Port Coastal Ocean Division，ASCE，1978，104(4):407-419.

［5］白玉川，杨细根，冀自青.波浪条件下海底管线与沙质海床间的相互作用［J］.天津大学学报，2011(1):64-68.(BAI Yuchuan，YANG Xigen，JI Ziqing.Interaction between submarine pipelines and sand seabed under the effect of wave［J］.Journal of Tianjin University，2011(1):64-68.(in Chinese))

［6］庄茁，张帆，岑松，等.ABAQUS 非线性有限元分析与实例［M］.北京:科学出版社，2005.(ZHUANG Zhuo，ZHANG Fan，CEN Song，et al.Nonlinear finite element analysis and examples ABAQUS［M］.Beijing:Science Press，2005.(in Chinese))

［7］车晓旭.多功能沉垫储油自升式平台沉垫上拔吸附力研究［D］.天津:天津大学，2012.(CHE Xiaoxu.Research on adsorption force of mat for multifunctional oil mat-type jack-up platforms［D］.Tianjin:Tianjin University，2012.(in Chinese))

［8］马小川.海南岛西南海域海底沙波沙脊形成演化及其工程意义［D］.青岛:中国科学院海洋研究所，2013.(MA Xiaochuan.Formation，evolution and engineering significance of submarine sand waves and sand ridges，southwest of Hainan Island［D］.Qingdao:Chinese Institute of Oceanology，2013.(in Chinese))