合理运用稚化思维,发展学生“再创造”能力
江苏如东县实验小学(226400) 丁杨华
合理运用稚化思维,发展学生“再创造”能力
江苏如东县实验小学(226400) 丁杨华
弗赖登塔尔认为,学习数学唯一正确的方法是实行“再创造”。为了让学生更好地实现“再创造”,应基于学生的数学现实、思维方式、思维过程三方面对学生思维进行合理稚化。合理稚化学生思维,顺应了学生的认知和思维规律,发展了学生的“再创造”能力。
合理运用 稚化思维 再创造
荷兰数学教育家弗赖登塔尔指出:传统的数学教学教授的是现成的知识,是违反教学法的。他认为学习数学唯一正确的方法是实行“再创造”,也就是让学生把要学习的知识用自己的思维方式,重新发现、创造出来。要让学生实现“再制造”,教师不能将现成的数学知识灌输给学生,要调整自己的教学行为,切合学生实际,合理稚化思维,让学生成为课堂学习的主人,在亲历“再创造”的过程中学习数学、理解数学、运用数学,感受数学的作用、价值与魅力。
这里所说的“稚化思维”,是指在教与学的双边活动中,教师有意识地将自己的思维退回到与学生相仿的水平,把熟悉的旧知当成新知,设身处地揣摩、迎合学生心态,用跟学生相匹配的认知能力、学习心境、探究活动来实现教与学和谐共振的一种教学思维。
下面简要谈谈合理运用稚化思维,发展学生“再创造”能力的一些粗浅做法。
一、以学生数学现实为稚化起点,引领学生数学“再创造”
在以往的课堂教学中,教师一般根据自身的知识水平及对教学内容的理解去设计教学,把知识的结果直接教授给学生,导致学生常常知其然,而不知其所以然。在进行各种可模仿、可借鉴的练习中,学生掌握得不错,但一旦题型稍有变化,学生就不能灵活变通了。为此,教师必须了解学生已有的数学现实,把学生新知学习的知识起点与逻辑起点作为自己稚化思维的起点,精心设计教学,放手让学生自主探究,有效引领学生实现“再创造”。
例如,在一年级上册“比一比”练习部分,最后有一道“比轻重”的思考题,如图1。

图1
学生一下子比较三种水果的轻重还是有难度的,而且两架天平一架不平衡、一架平衡,学生很难辨清。教材前面所出现的均是只有一架天平而且是不平衡的情况,学生借助已有的生活经验——压跷跷板的经历:沉下去的一边重,翘上去的一边轻,很容易就理解了一架天平两端物体的轻重。但是图1情况复杂多样,学生无从下手。为此,教师根据学生已有的知识经验来稚化思维,设计了图2来过渡。教师引导学生逐一观察得出苹果比梨重,梨比草莓重,学生很快就发现:借助梨这座“桥梁”,就能得出苹果最重,梨其次,草莓最轻。然后出示图1,一架平衡的、一架不平衡天平中的三个量;最后解决图3,两架均平衡天平中的三个量。因为有了图2的有效引领,教师无需多言,一切水到渠成,学生顺利实现了“再创造”。
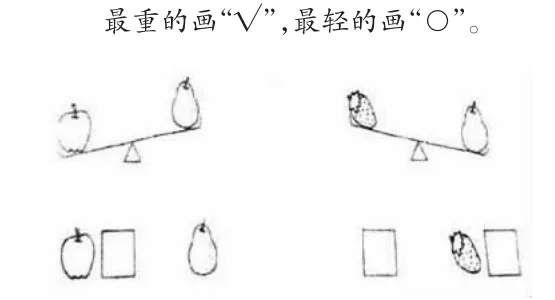
图2
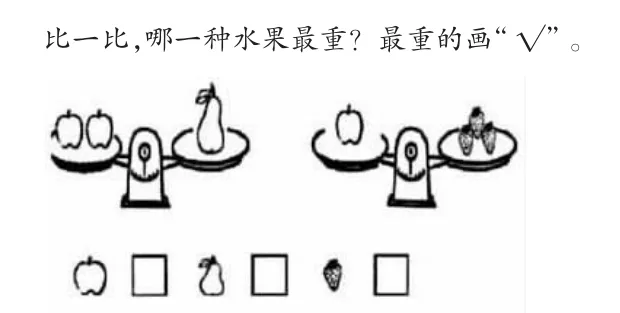
图3
纵观以上教学过程,教者较好地把握了学生已有的知识经验和现有的学习状况,准确地以学生的认知起点为稚化起点设计了教学,为学生搭建了“再创造”的平台。巧妙的设计极大地提高了学生的参与程度,学生们个性张扬,勇于提出自己的见解,较好地发掘出学生的潜能,发展了其创造能力。
二、以学生思维方式为稚化重点,促进学生数学“再创造”
在日常的数学教学中,如果教师仅就例题、习题滔滔不绝地讲授,过分去追求解决问题思路的单一化、简洁化、技巧化,课堂就会成为教师表演的舞台,学生亦成为可有可无的旁观者。这样学生势必产生思维惰性,对所学的新知只会被动接受和机械记忆。为此,我们的教学不能背离学生的认知规律,要把学生的思维方式作为稚化重点,及时把握学生的思维动向,为学生提供更多的交流、展示的时间与空间,让学生在多样化的解题策略中实现数学“再创造”,从而拓展学生的思维深度,提升学生应用知识的能力。
例如,在教学三年级下册“用连除计算解决的实际问题”时,首先用PPT课件出示主题图,引导学生观察:两个书架,每个书架4层,一共有224本书。学生根据已知信息提出问题:平均每个书架每层放多少本?教者放手让学生独立思考,尝试解答,让学生四人为一组交流解题方法。最后集体汇报交流成果。如方法一:224÷2=112(本),112÷4=28(本);方法二:4×2=8(层),224÷8=28(本)。汇报的学生还逐一介绍了解题思路和每步算式所表达的意思。教者微笑地点头问:还有没有不同的方法?第五小组的小叶同学站起来介绍了方法三:224÷4=56(本),56÷2=28(本)。学生们纷纷摇头,都认为这样列式没有意义。教师未置可否,小叶同学指着主题图继续介绍:我们可以把这两个书架并排放置在一起,这样“224÷4=56(本)”就表示新拼成的大书架的一层有56本书,再除以2,就表示原来每个书架每层平均有28本书;如果两个书架不拼在一起,“224÷4=56(本)”就是表示两书架平均一层可以放书多少本。这时,学生们纷纷点头表示赞同。
整个教学过程,教师放手让学生独立思考、合作交流、汇报展示,教师充分估计到大多数学生在知识方面的缺陷和不完整性,巧妙地稚化自己的思维,让另辟蹊径完成“再创造”的学生展示意料之外的解法,让学生体验“再创造”带来的深刻思维和丰富智慧,实现了生生、师生思维的和谐共振。
三、以展示学生思维过程为稚化难点,实现学生数学“再创造”
对于教学难点的突破,教师要准确把握学生思维特点和思维心理,对学生接受新知的能力做出符合实际的估量,合理稚化自己思维与教学行为,从学生的视角感受学生学习新知的困难所在,精心创设“思维情境”,使师生思维“合拍”,设计出与学生思维发展相吻合的教学流程,把教师的教与学生的学融为一体,让学生参与并见证新知的形成过程,促进学生数学“再创造”的顺利达成,实现对新知的积极构建。
例如,在学习六年级下册“圆柱和圆锥”之后的练习课上,我精心设计了这样一道题:某品牌一支儿童牙膏出口处直径为5毫米,豆豆每次刷牙都挤出12毫米长的牙膏,这支牙膏可供他用36次。该牙膏推出的新包装只是将出口处直径改为6毫米,豆豆还是按习惯每次挤出12毫米长的牙膏,新包装的这支牙膏他能用几次?题目刚出示完,班上的几个活跃分子就窃窃私语:“每次挤出的是小圆柱,牙膏的总体积不变,这题不难。”学生们拿起笔算起来。5分钟过去了,还没有人举手,这时小管同学站起来说:“老师,太难算了,将直径5改为4吧。”“对啊!这个数字老师没想好,这么难算,没有意义。”其他同学纷纷附和。我无奈地说:“好吧,就把5改为4吧。”“不要,我已经算出来啦!3.14×(5÷2)2× 12×36=8478(立方毫米),这算的是牙膏的体积;再算3.14×(6÷2)2×12=339.12(立方毫米),它是新包装后每次用的牙膏量;最后8478÷339.12=25(次)。”小秦同学滔滔不绝地汇报。“我们也是按这样的思路做的,就是没算好。”其他同学略带困惑地说。我笑着说:“方法都会就行了,就是难算啊!”“谁说难算的,您不是教过我们方程吗?我是这样做的,设新包装的牙膏它能用x次,列式为3.14×(6÷2)2×12×x=3.14×(5÷2)2× 12×36,根据等式的性质方程两边同时除以3.14和12,方程就简化为9x=(5÷2)2×36,x=25。”小何同学激动、兴奋地说。“对呀,这个方程多好啊!简便、快捷、实用。”我也点头附和。“我还有更简便的方法。”小熙同学迫不及待地站起来说:“两次挤出牙膏底面直径的比是5∶6,底面积的比就是52∶62,也就是25∶36,因为前后每次挤出的长度都是12毫米,所以两次挤出的体积比还是25∶36,新包装前可用36次,总体积不变,每次挤出的量和使用次数是成反比例关系的,所以新包装可使用25次。”“真棒!”教室里响起了经久不息的掌声。
教者巧妙地稚化思维、因势利导,带领学生经历了“改数字——算术法——解方程——用比转化”四个阶段,顺利突破了教学预设中的难点,帮助学生达成多种不同思维层次的“再创造”。
四、以克服学生思维障碍为稚化原点,完善学生数学“再创造”
从学生的实际心智状态出发,教者将自己的思维稚化到与学生相契合、相顺应的状态,设身处地地将学生的困惑与思维障碍作为教学设计的原点,引领学生将难题的解答还原为生动活泼的探究活动和数学“再创造”活动。这样,教师的思维“学生化”,有效避免了以教师的思维替代学生的思维,教学过程成为学生自主探究的学习过程,新知的学习会进入一种循序渐进、自然流畅的境地。
例如,在六年级下册“百分数的应用”单元练习时,遇到一道题:2008年我国公布的个人所得税征收标准中,个人月收入2000元以下不征税,月收入超过2000元,超过部分按以下标准征税:不超过500元的部分,5%;超过500~2000元的部分,10%;超过2000~5000元的部分,15%。张叔叔三月份工资纳税385元,他三月份工资应该是多少元?对于此题,全班46名同学仅有两人做对。学生的思维障碍在哪里?通过对学生的访谈了解,其思维的障碍主要体现在三点:一是要逆向思维,由知道纳税额求工资;二是不明白分段计税的意思;三是不明白计税部分每段分别是多少元。找准学生的这三点思维障碍,教者精心做了设计:1.这里分段计税是什么意思?你能举例说一说吗?2.分别算一算工资2100元、2600元、3500元、3900元、4500元分别纳税多少元?3.纳税25元、35元、150元,工资分别应该是多少元?4.纳税385元,工资应该是多少呢?针对以上设计,教者放手让学生独立完成、展示汇报交流,结果所有问题迎刃而解。
可见,教者在学生思维障碍处稚化思维,能引领学生回归知识的原点,促使学生积极思考探究,既强化了对障碍根源的认识与分析,提高了“免疫力”,又让学生在解决问题的过程中发展、完善自身的“再创造”能力。
总之,在今后的数学教学活动中,我们教者不能仅从教本出发,更不能从自身的一厢情愿出发,而应该从学生已有的知识经验和思维水平出发,合理稚化思维,顺应学生的认知习惯与思维方式,让学生在亲历知识形成的过程中,发展“再创造”能力,全面提升学生的数学学习力。
(责编 黄春香)
G623.5
A
1007-9068(2015)05-068

