孕育数学理性 培植理性气质
清华大学附属小学(100084) 汤卫红(特级教师)
孕育数学理性 培植理性气质
清华大学附属小学(100084) 汤卫红(特级教师)
儿童为什么要学习数学?教育哲学理论认为:“通过数学学会思维!”数学的思维是和数学最核心的本质特征紧密关联的,这种核心本质应该是理性精神。如何理解数学理性?如何培育学生的理性精神、理性气质?这都是数学教师必须思考的话题。
数学 数学理性 儿童 数学学习
数学是人类智慧的荣耀,是人类理性文明的火车头。理性是数学特有的气质,数学理性是数学最为重要的文化精神,深刻影响着人类的精神生活,是一种普遍化的力量,使人类的思维得以运用到最完善的程度,满足人类对宇宙的探求,甚至影响着现代文明的进程。数学课程体现理性是数学学科的内在要求,数学理性也是数学教育承载的重要的育人功能。
一
何为“理性”?词典中解释为:“指属于判断、推理等活动的(跟‘感性’相对):~认识。”(见《现代汉语词典》2002年增补本,商务印书馆)不难看出,感性是理性存在的基础,人最初对事物的认识总是从感性开始的,感性属于认识过程的低级阶段,而理性是感性飞跃发展的高级阶段。对事物感性的认识往往是片面的、现象的和外部联系的,而对事物的理性认识往往是全体的、本质的和内部联系的。词典主要是从认知活动的角度对“理性”的基本含义给出解释。就数学理性而言,主要是指孕育于古希腊文明,并伴随着近代自然科学的形成和发展逐步稳定的西方理性精神,即人们在数学活动中形成的追求对研究对象本质、规律和内部联系的准确把握,追求抽象的、超验的思维取向,能够不断反思、批判自己并以此开辟前进道路的价值观和行为规范。更为全面地讲,我们通常所说的数学理性亦包括数学理性思维。
在人类文明的进程中,数学理性表现为人类对真理的不懈追求,表现为以严密的、超验的、科学的思维方法抽象、概括、判断和推理。它大大促进了人类思想的解放,提高和丰富了人类的精神水平。因此,数学教育要通过培养理性思维、培育理性精神、培植理性气质,提高思维的深刻性、灵活性、独创性、批判性和敏捷性,促进学生形成求真、求实品格,成为更完全、更丰富、更有力量的人。于数学教学而言,理性会让我们直抵数学教学的核心,确证数学教学的本质意义,以至理性成为数学教学得以安身立命的文化支柱以及数学教学成功的文化力量。数学教学只有孕育理性才能不断生长,数学学习只有孕育数学理性才能根深叶茂。
二
针对新课改初期出现的“非数学化”倾向,不少教师大声疾呼:数学课要有“数学味”!其中,最重要的就是要孕育数学理性。对于处于具体运算阶段的小学儿童而言,他们的思维一般还不能离开具体事物的支持,正从具体形象思维为主逐步向抽象逻辑思维过渡。显然,教师不能硬生生地直接阐释数学的概念、法则,不能过早地脱离感性直接进行理性的抽象教学,否则数学的艰涩和抽象会让学生丧失对数学的兴趣和信心。因此,基于感性,孕育理性是数学教育的应然选择。
基于感性意味着没有感性经验的积累和支撑就没有理性认识的飞跃,孕育理性意味着没有逐步抽象的引导就不能形成概念、判断、推理,就不能到达本质,揭示联系。要获得感性经验,就必须以观察、模仿、尝试、实验、猜想等活动经验为支撑。在此基础上,通过思考、分析、概括、想象等活动让感性经验向抽象和普遍发展。毋宁说这是对教师的理性气质的一种要求。在实际教学中,我们的课堂往往不缺乏丰富、具体的操作活动,甚至学生也不缺乏感性经验的积累,但往往由于教师的“不作为”,学生会耽于感性的“温柔之乡”,而忘记对数学本质的探求。例如,“三角形三边关系”教学,不少课堂上都会出现为“两根小棒长度之和等于第三根时,到底能不能围成三角形”而争执不下的情况,而教师解释为“制作和操作的误差”,并用多媒体动画演示“围”的过程(甚至请放大镜出马放大两根短棒之间的缝隙),显然不能让固执地认为“能”者所信服。感性经验造成的“伪事实”遮蔽了学生对数学本质的正确把握。理性能让我们去伪存真、由表及里。引导学生基于感性经验思考:将两根等长的小棒叠在一起,其中一根截成两段,这时三根小棒长度有何关系?相反地,如果用长棒去量两根短棒的长度之和,你会怎么摆?这时会出现什么情况?三根小棒之间是否围成一个区域?如果以两根短棒与长棒相接的端点为中心向外旋转,想象短棒外端运动的轨迹。观察这个轨迹,你明白了什么?从确认“重合时首尾相连但未构成三角形”这个理性认同的事实出发,以运动轨迹促进学生理性思考两端点难以觉察但无可置疑地“一动即分”。以大趋势把握小瞬间就能够击穿感性“伪事实”,抵达本质规律,这正是数学理性的重要力量。更为重要的是,超越经验、严谨求实、用理性思考力量探寻真知的理性精神和科学态度对学生的影响无疑超越于知识而更为巨大。
数学教育孕育数学理性对教师的数学理性提出了挑战,教师需要从以下几个方面提高自身的修养。
第一,丰富和完善数学本体性知识,超越教材,把握所教内容的数学本质,探寻其本原意义。这是课堂孕育数学理性的前提。只有教师洞察到问题的数学本质,才有可能引导学生在浅显中见深刻,具体中现理性。例如,“可能性”教学,摸球游戏中出现摸到某种球的频率与概率完全背离的现象,如果明白概率知识,我们反而能抓住契机,让学生感受数据的随机性,再通过数据的不断增加体会频率稳定于概率附近这一规律。
第二,回归数学历史发展的本来面目,把握人类思维发展中的那些关键性步子。学生对数学的认知过程与数学发展史的过程相似,历史上人类所遇到的困难往往也是学生认知的障碍。而人类对数学认知的过程往往是数学理性不断作用的过程,是不断向数学本质迈进的过程。波利亚曾说:“在了解人类是怎样获得某些事实或概念的过程之后,我们就能更好地去判断我们的孩子应当怎样去学习这些知识。”在这个基础上的学习便是数学理性不断提升的过程。
第三,把握数学学习心理,遵循心理发展的规律,聚焦于学生学习数学新知的认知过程,触及新知所需思维方式的变换。只有教师从理性的高度把握真实的数学学习过程,才可能让学生的数学认识由具体向形式飞跃,由感性向理性提升。例如,学生对面积与周长的混淆是由于弄不清周长乃长与宽测度之和,而面积是两维测度之积,这是加法结构对乘法结构干扰的一种表现形式。把握住这一点,就可以在教学实践中构造对比图形(如长方形由公共边分成周长相等但面积不等的两部分)以促进学生理性认识的形成。另一方面,通过操作单位正方形测量面积,发展儿童的空间表征能力有利于长度表征与面积表征的分化,从而真正建立起对面积概念的理性认识。
三
当我们认同发展儿童数学理性思维,培植理性精神的价值,并将之作为数学教育的重要目标时,我们更加关注如何做,做到什么程度。我以为应从以下几个方面进行探索与实践。
1.于直观操作中抽象实在,凸显要义
数学课堂中的直观操作绝不仅仅是操作,一定是服务于理性认识的需要,仅仅这种理性认识不是一蹴而就的,但我们从一开始就要朝这个目标前进,而不是停留于具体的操作经验。只有逐步融入理性思考的操作才是数学的活动。比如,对于分数,张奠宙教授说:“对于,儿童如果脑子里始终是半个大饼,那就还没有学好分数。”更进一步,分数的教学绝不能停留于对一个物体、一个计量单位、许多物体组成的一个整体进行平均分操作。如果没有把这些操作的经验适时抽象,儿童就会出现如下的错误:
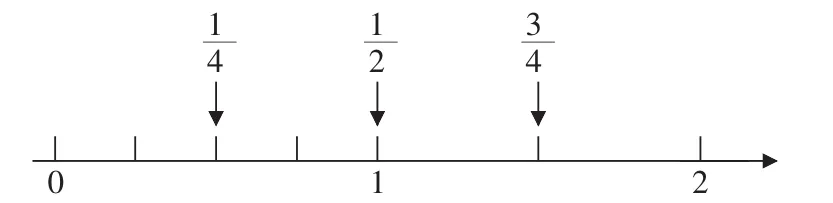
史宁中教授强调分数的“无量纲性”,对单位“1”的抽象是实现分数本质建构的关键。所以,在学生根据各种情形说出分数意思的基础上,通过多媒体将各种平均分的对象对应到数轴上的“1”,促进学生认识到抽象的自然数“1”能够涵盖林林总总可以用“1”表示的事物:1个饼、1米、1盘桃……当它们都抽象为“1”时,并无本质差别。而各种情形中的等亦需对应数轴上相应的点,让学生领悟每个分数作为一个数的概括性与抽象性。
2.于感性经验中突破超越,跃向本质
数学知识作为一种抽象的存在,很多时候超越于经验,必须借助于理性的抽象思考才能领悟其本质。教师在学生已有经验的基础上,搭建合理的想象起飞跑道,才能助其实现抽象,达到对数学知识本质属性的理性认识。仅通过文字、符号的抽象表达并不能很好地培养学生的数学理性。例如,观察物体中学生很容易提出“看到的一前一后两个正方体的面并非等大,为什么却要画成一样大”这样的问题。教师就应当清楚数学上所画的视图不同于美术中的透视,而是用平行光线正投影得到的物体轮廓。如何跨越经验与抽象的视图之间的鸿沟?教师不妨让学生逐渐远离物体,体会长距离下人的视线对于小物体趋近于平行线时所看到的两个正方形趋近等大。另一方面,这种画法所得结果的唯一性避免了根据人眼观察物体因距离远近而结果各不相同不利于数学交流的尴尬,从而体会三视图画法的优越性,感悟数学理性的价值。
3.于相异无关中寻同求联,彰显结构
寻找数学知识之间的联系,形成横贯纵通的统一结构亦是人类理性的不懈追求。教师应当从高观点、高视角俯视学生所学的数学知识,引导其寻求一个个看似相互独立、已有定论的知识的相同属性,建立内在联系,甚至走向结构化,这对促进学生的数学理性形成和数学内在美的认同大有裨益。例如,学生所学的平面图形都有各自的面积公式,除了引导其建构知识树,更具理性意味的问题是“能否选择一个公式作为统一的面积公式?说说你的理由。”在寻找联系中,学生既能体会到上位思考的力量,又能感悟到量变中的质变,质变中量变的统一,经常的理性的哲思必将塑造学生的理性气质。
(责编 金 铃)
G623.5
A
1007-9068(2015)08-001

